高中物理教科版必修第一册 2.3匀变速直线运动位移与时间的关系课件(共39张PPT)
文档属性
| 名称 | 高中物理教科版必修第一册 2.3匀变速直线运动位移与时间的关系课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-07-16 09:47:52 | ||
图片预览







文档简介
(共39张PPT)
第3节 匀变速直线运动位移与时间的关系
课 标 定 位
1.掌握利用v-t图像求解位移的方法。
2.掌握位移—时间的关系式并能灵活应用。
3.理解公式的矢量性,能运用速度与位移的关系分析、解决匀变速直线运动实际问题。
素 养 阐 释
1.结合位移公式的推导方法,感受利用极限思想解决物理问题的科学思维方法。
2.通过公式 的应用培养用物理语言表达物理规律的科学思维方式。
3.结合公式分析实际问题,增强将物理知识应用于实际生活的意识,培养科学态度与责任这一素养。
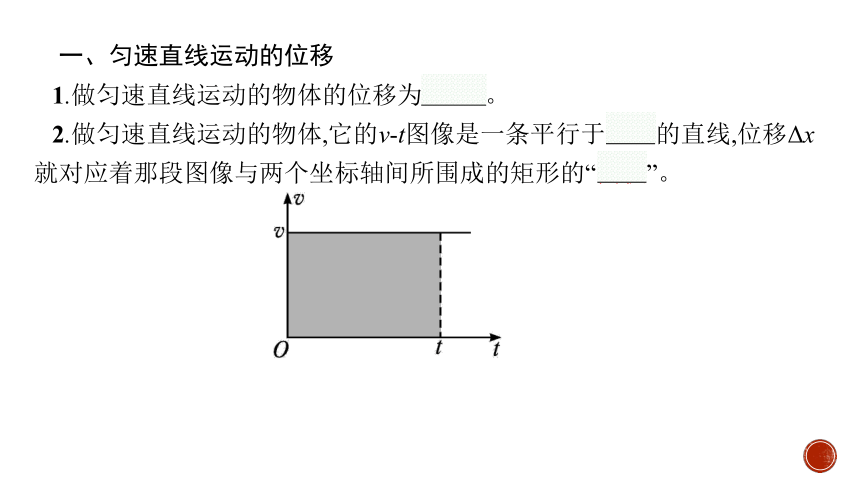
一、匀速直线运动的位移
1.做匀速直线运动的物体的位移为Δx=vt。
2.做匀速直线运动的物体,它的v-t图像是一条平行于横轴的直线,位移Δx就对应着那段图像与两个坐标轴间所围成的矩形的“面积”。
二、匀变速直线运动的位移公式
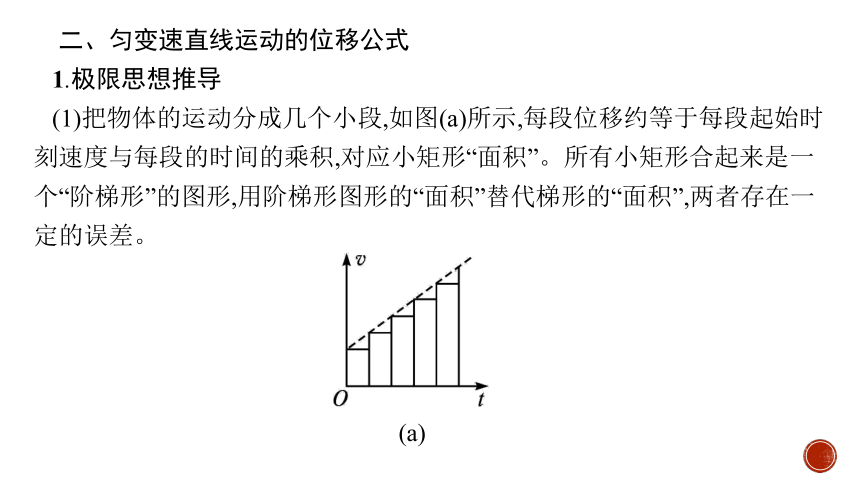
1.极限思想推导
(1)把物体的运动分成几个小段,如图(a)所示,每段位移约等于每段起始时刻速度与每段的时间的乘积,对应小矩形“面积”。所有小矩形合起来是一个“阶梯形”的图形,用阶梯形图形的“面积”替代梯形的“面积”,两者存在一定的误差。
(a)
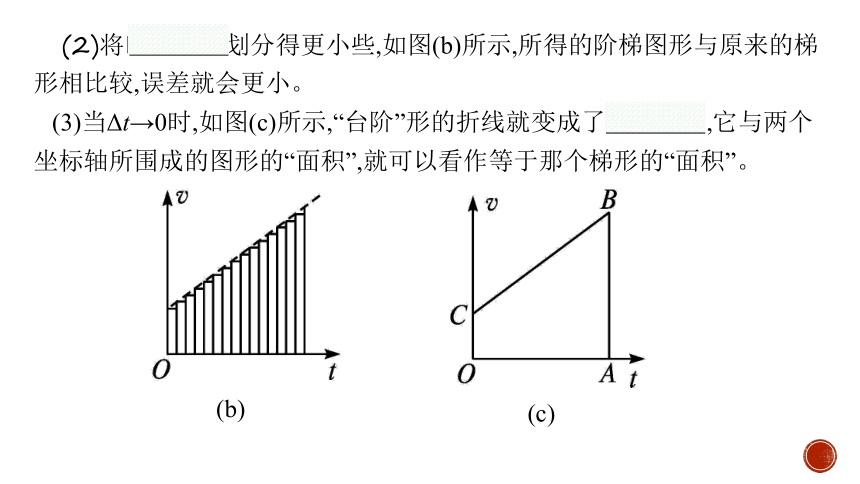
(2)将时间间隔划分得更小些,如图(b)所示,所得的阶梯图形与原来的梯形相比较,误差就会更小。
(3)当Δt→0时,如图(c)所示,“台阶”形的折线就变成了一条直线,它与两个坐标轴所围成的图形的“面积”,就可以看作等于那个梯形的“面积”。
(b)
(c)
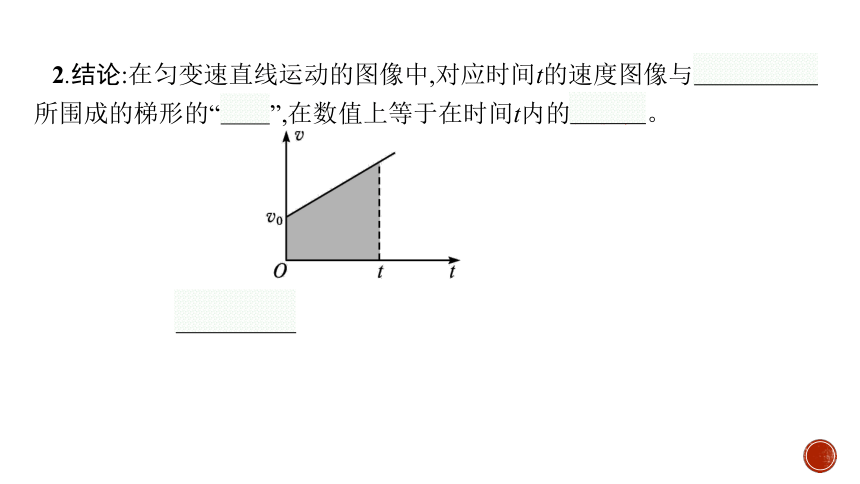
2.结论:在匀变速直线运动的图像中,对应时间t的速度图像与两个坐标轴所围成的梯形的“面积”,在数值上等于在时间t内的位移值。
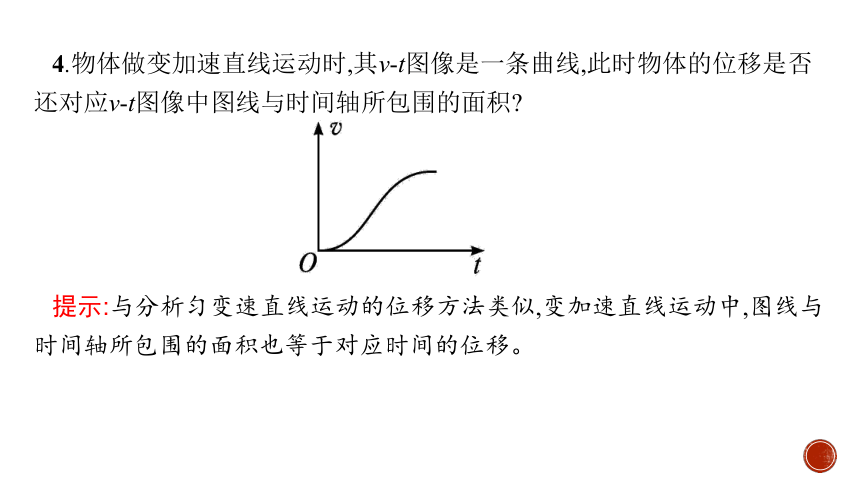
4.物体做变加速直线运动时,其v-t图像是一条曲线,此时物体的位移是否还对应v-t图像中图线与时间轴所包围的面积
提示:与分析匀变速直线运动的位移方法类似,变加速直线运动中,图线与时间轴所包围的面积也等于对应时间的位移。
【思考讨论】
1.判断下列说法的正误。
(1)位移公式 仅适用于匀变速直线运动。( )
(2)对于一个做匀加速直线运动的物体加速度越大,位移越大。( )
(3)初速度越大,时间越长,匀变速直线运动物体的位移一定越大。( )
(4)匀变速直线运动的位移与初速度、加速度、时间三个因素有关。
( )
(5)x-t图像中的图线就是物体的实际运动轨迹。( )
√
×
×
√
×
2.一辆卡车在平直的公路上做匀速直线运动,速度为10 m/s,突然司机发现前方15 m有一障碍物,立即紧急刹车(忽略司机的反应时间),紧急刹车过程中的加速度的大小是5 m/s2,回答下列问题:
(1)我们求卡车刹车后某时间内的位移时,能否直接利用公式 求解
(2)从开始刹车到车完全停下来需要经过多长时间
(3)刹车开始后1 s内的位移大小
(4)卡车刹车过程运动的总位移为多少
(5)求卡车从刹车到停下来全程的平均速度。
【问题引领】
航天飞机着陆时,若已知航天飞机着陆时的速度和着陆打开阻力伞后做匀减速直线运动的加速度,求解其位移时注意什么问题
提示:应先计算出航天飞机从着陆到停止所用的时间,将计算出的时间与题中所已知的时间相比较,然后进行相应的计算。若题中所给的时间小于或等于计算出的时间,将所给的时间直接代入公式 计算;若题中所给的时间大于计算出的时间,则计算出飞机速度减小到零所发生的位移即可。
【归纳提升】
【典型例题】
【例题1】 汽车刹车前速度为4 m/s,刹车获得加速度大小为0.4 m/s2,求:
(1)汽车刹车开始后第20 s末的速度;
(2)汽车刹车开始后20 s内滑行的距离s0;
(3)静止前2 s内汽车滑行的距离s。
答案:(1)0 (2)20 m (3)0.8 m
解析:(1)设汽车刹车停下来的时间为t0,根据v=v0+at0得t0=10 s
所以汽车刹车开始后第20 s末的速度为0。
【变式训练1】 一辆汽车正在平直的公路上以72 km/h的速度行驶,司机看见红色信号灯便立即踩下制动器,此后,汽车开始做匀减速直线运动。设汽车减速过程的加速度大小为5 m/s2,求:
(1)开始制动后,前2 s内汽车行驶的距离;
(2)开始制动后,前5 s内汽车行驶的距离。
答案:(1)30 m (2)40 m
【问题引领】
下图为一运动物体的位移x(或速度v)与时间t的函数关系图像。此图线在x-t或v-t中各表示的意义是什么
提示:图线在x-t中表示物体做与规定正方向相反的匀速直线运动,初位移为x0。图线在v-t中表示物体做匀减速直线运动,初速度为v0。
【归纳提升】
1.x-t图像:以时间为横坐标,以位移为纵坐标,描述位移随时间变化情况的图像叫位移—时间图像。
2.x-t图像的意义
3.几种常见的位移—时间图像
(1)静止物体的x-t图像是平行于时间轴的直线,如图中直线A。
(2)匀速直线运动的x-t图像是一条倾斜的直线,如图中直线B和C,其斜率表示速度。其中B沿正方向运动,C沿负方向运动。
(3)匀变速直线运动的x-t图像:由位移 可以看出,x是t的二次函数。当v0=0时,匀变速直线运动的x-t图像是顶点在坐标原点的一部分曲线,曲线上某点切线的斜率表示那一时刻的速度,图中切线斜率增大,质点的速度逐渐增大。
【典型例题】
【例题2】 图(a)是一个物体沿直线运动的x-t图像。求:
(a)
(b)
(1)第5 s末的速度大小;
(2)0~60 s内的总路程;
(3)在v-t坐标中作出0~60 s内物体的速度—时间图像。
答案:见解析
解析:(1)0~10 s内匀速运动的速度
即第5 s末的速度大小为2 m/s。
(2)0~10 s内的路程s1=20 m
10~40 s内的路程s2=0
40~60 s内的路程s3=20 m
所以0~60 s内的总路程s=s1+s2+s3=40 m。
(3)0~10 s内速度v1=2 m/s
10~40 s内速度为0
40~60 s内速度 ,
方向与原速度方向相反,速度—时间图像如图所示。
分析图像问题要注意
(1)分析图像问题时首先注意坐标轴所对应的物理量,确定是x-t图像还是v-t图像。
(2)不同图像对应斜率的含义不同,x-t图像的斜率表示物体速度的大小和方向,而v-t图像的斜率表示物体加速度的大小和方向。
【变式训练2】 (多选)下图是甲、乙、丙、丁、戊五个运动物体相对同一原点的位移—时间图像。下面有关说法正确的是( )
(a)
(b)
(c)
A.甲、乙运动的出发点相距x0 B.乙比甲早出发t1的时间
C.丙在0~2 s内,物体的位移大于2 m D.丁、戊两物体在25 s时相遇
答案:AD
解析:由图可知,乙从原点出发,甲从距原点x0处出发,则两物体的出发点相距x0,故A正确;甲在t=0时刻开始运动,而乙在t1时刻开始运动,则甲比乙早出发t1时间,故B错误;丙在0~2 s内,物体的位移为Δx=0-0=0,故C错误;丁、戊两物体在25 s时到达同位置而相遇,故D正确。
【问题引领】
只能用位移公式求匀变速直线运动的位移吗
提示:不。可以灵活运用各种不同的关系和方法求匀变速直线运动的位移。如用平均速度、运动图像、比例关系等。
【归纳提升】
1.平均速度
(1)结论:做匀变速直线运动的物体,在一段时间t内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初末速度矢量和的一半。
(2)推导:设物体的初速度为v0,做匀变速直线运动的加速度为a,t末的速度为vt。
2.逐差相等
(1)结论:在任意两个连续相等的时间间隔T内,位移之差是一个常量,即Δx=xⅡ-xⅠ=aT2。
注意:则xⅠ=x1,xⅡ=x2-x1 ③
由①②③得Δx=xⅡ-xⅠ=aT2。
公式Δx=aT2的应用:一是用以判断物体是否做匀变速直线运动,二是用以求加速度。
【典型例题】
【例题3】 从车站开出的汽车,做匀加速直线运动,走了12 s后发现,还有乘客没上来,于是立即做匀减速直线运动至停车,共历时20 s,行进50 m,求其最大速度。
答案:5 m/s
解析:法一(基本公式法) 设最大速度为vmax,由题意得
【变式训练3】 如图所示,一小球(可视为质点)沿斜面匀加速下滑,依次经过A、B、C三点。已知xAB=18 m,xBC=30 m,小球经过AB和BC两段所用的时间均为2 s,则小球经过A、B、C三点时的速度大小分别是( )
A.12 m/s,13 m/s,14 m/s B.10 m/s,14 m/s,18 m/s
C.8 m/s,10 m/s,16 m/s D.6 m/s,12 m/s,18 m/s
答案:D
A.加速度大的物体位移大
B.初速度大的物体位移大
C.末速度大的物体位移大
D.以上说法都不对
答案:D
解析:由 知,x的大小与初速度、加速度、时间都有关,t一定时,x与两个量有关,不能简单地说初速度大或加速度大,位移一定大,A、B、C均错,D对。
2.(x-t图像)下列图像均能正确反映物体在直线上的运动,在t=2 s内物体位移最大的是( )
答案:B
解析:选项A、C、D中2 s内物体位移均为0,选项B中物体一直向正方向运动,B正确。
3.(x-t图像)(多选)下图为在同一直线上运动的A、B两质点的x-t图像,由图可知( )
A.t=0时,A在B的前面
B.B在t2时刻追上A,并在此后运动到A的前面
C.B开始运动的速度比A的小,t2时刻后才大于A的速度
D.A运动的速度始终比B的大
答案:AB
解析:t=0时,A在原点正方向x1位置处,B在原点处,A在B的前面,A对。t2时刻两图线相交,表示该时刻B追上A,并在此后运动到A的前面,B对。B开始运动的速度比A的小,t1时刻后A静止,B仍然运动,C、D错。
4.(刹车类问题)汽车以20 m/s的速度做匀速直线运动,刹车后的加速度大小为5 m/s2,那么开始刹车后2 s内与开始刹车后6 s内汽车通过的位移之比为
( )
A.1∶1 B.1∶3
C.3∶4 D.4∶3
答案:C
5.(匀变速直线运动基本公式的应用)一物体做初速度为零的匀加速直线运动,加速度为a=2 m/s2,求:
(1)第5 s末物体的速度多大
(2)前4 s的位移多大
(3)第4 s内的位移多大
答案:(1)10 m/s (2)16 m (3)7 m
第3节 匀变速直线运动位移与时间的关系
课 标 定 位
1.掌握利用v-t图像求解位移的方法。
2.掌握位移—时间的关系式并能灵活应用。
3.理解公式的矢量性,能运用速度与位移的关系分析、解决匀变速直线运动实际问题。
素 养 阐 释
1.结合位移公式的推导方法,感受利用极限思想解决物理问题的科学思维方法。
2.通过公式 的应用培养用物理语言表达物理规律的科学思维方式。
3.结合公式分析实际问题,增强将物理知识应用于实际生活的意识,培养科学态度与责任这一素养。
一、匀速直线运动的位移
1.做匀速直线运动的物体的位移为Δx=vt。
2.做匀速直线运动的物体,它的v-t图像是一条平行于横轴的直线,位移Δx就对应着那段图像与两个坐标轴间所围成的矩形的“面积”。
二、匀变速直线运动的位移公式
1.极限思想推导
(1)把物体的运动分成几个小段,如图(a)所示,每段位移约等于每段起始时刻速度与每段的时间的乘积,对应小矩形“面积”。所有小矩形合起来是一个“阶梯形”的图形,用阶梯形图形的“面积”替代梯形的“面积”,两者存在一定的误差。
(a)
(2)将时间间隔划分得更小些,如图(b)所示,所得的阶梯图形与原来的梯形相比较,误差就会更小。
(3)当Δt→0时,如图(c)所示,“台阶”形的折线就变成了一条直线,它与两个坐标轴所围成的图形的“面积”,就可以看作等于那个梯形的“面积”。
(b)
(c)
2.结论:在匀变速直线运动的图像中,对应时间t的速度图像与两个坐标轴所围成的梯形的“面积”,在数值上等于在时间t内的位移值。
4.物体做变加速直线运动时,其v-t图像是一条曲线,此时物体的位移是否还对应v-t图像中图线与时间轴所包围的面积
提示:与分析匀变速直线运动的位移方法类似,变加速直线运动中,图线与时间轴所包围的面积也等于对应时间的位移。
【思考讨论】
1.判断下列说法的正误。
(1)位移公式 仅适用于匀变速直线运动。( )
(2)对于一个做匀加速直线运动的物体加速度越大,位移越大。( )
(3)初速度越大,时间越长,匀变速直线运动物体的位移一定越大。( )
(4)匀变速直线运动的位移与初速度、加速度、时间三个因素有关。
( )
(5)x-t图像中的图线就是物体的实际运动轨迹。( )
√
×
×
√
×
2.一辆卡车在平直的公路上做匀速直线运动,速度为10 m/s,突然司机发现前方15 m有一障碍物,立即紧急刹车(忽略司机的反应时间),紧急刹车过程中的加速度的大小是5 m/s2,回答下列问题:
(1)我们求卡车刹车后某时间内的位移时,能否直接利用公式 求解
(2)从开始刹车到车完全停下来需要经过多长时间
(3)刹车开始后1 s内的位移大小
(4)卡车刹车过程运动的总位移为多少
(5)求卡车从刹车到停下来全程的平均速度。
【问题引领】
航天飞机着陆时,若已知航天飞机着陆时的速度和着陆打开阻力伞后做匀减速直线运动的加速度,求解其位移时注意什么问题
提示:应先计算出航天飞机从着陆到停止所用的时间,将计算出的时间与题中所已知的时间相比较,然后进行相应的计算。若题中所给的时间小于或等于计算出的时间,将所给的时间直接代入公式 计算;若题中所给的时间大于计算出的时间,则计算出飞机速度减小到零所发生的位移即可。
【归纳提升】
【典型例题】
【例题1】 汽车刹车前速度为4 m/s,刹车获得加速度大小为0.4 m/s2,求:
(1)汽车刹车开始后第20 s末的速度;
(2)汽车刹车开始后20 s内滑行的距离s0;
(3)静止前2 s内汽车滑行的距离s。
答案:(1)0 (2)20 m (3)0.8 m
解析:(1)设汽车刹车停下来的时间为t0,根据v=v0+at0得t0=10 s
所以汽车刹车开始后第20 s末的速度为0。
【变式训练1】 一辆汽车正在平直的公路上以72 km/h的速度行驶,司机看见红色信号灯便立即踩下制动器,此后,汽车开始做匀减速直线运动。设汽车减速过程的加速度大小为5 m/s2,求:
(1)开始制动后,前2 s内汽车行驶的距离;
(2)开始制动后,前5 s内汽车行驶的距离。
答案:(1)30 m (2)40 m
【问题引领】
下图为一运动物体的位移x(或速度v)与时间t的函数关系图像。此图线在x-t或v-t中各表示的意义是什么
提示:图线在x-t中表示物体做与规定正方向相反的匀速直线运动,初位移为x0。图线在v-t中表示物体做匀减速直线运动,初速度为v0。
【归纳提升】
1.x-t图像:以时间为横坐标,以位移为纵坐标,描述位移随时间变化情况的图像叫位移—时间图像。
2.x-t图像的意义
3.几种常见的位移—时间图像
(1)静止物体的x-t图像是平行于时间轴的直线,如图中直线A。
(2)匀速直线运动的x-t图像是一条倾斜的直线,如图中直线B和C,其斜率表示速度。其中B沿正方向运动,C沿负方向运动。
(3)匀变速直线运动的x-t图像:由位移 可以看出,x是t的二次函数。当v0=0时,匀变速直线运动的x-t图像是顶点在坐标原点的一部分曲线,曲线上某点切线的斜率表示那一时刻的速度,图中切线斜率增大,质点的速度逐渐增大。
【典型例题】
【例题2】 图(a)是一个物体沿直线运动的x-t图像。求:
(a)
(b)
(1)第5 s末的速度大小;
(2)0~60 s内的总路程;
(3)在v-t坐标中作出0~60 s内物体的速度—时间图像。
答案:见解析
解析:(1)0~10 s内匀速运动的速度
即第5 s末的速度大小为2 m/s。
(2)0~10 s内的路程s1=20 m
10~40 s内的路程s2=0
40~60 s内的路程s3=20 m
所以0~60 s内的总路程s=s1+s2+s3=40 m。
(3)0~10 s内速度v1=2 m/s
10~40 s内速度为0
40~60 s内速度 ,
方向与原速度方向相反,速度—时间图像如图所示。
分析图像问题要注意
(1)分析图像问题时首先注意坐标轴所对应的物理量,确定是x-t图像还是v-t图像。
(2)不同图像对应斜率的含义不同,x-t图像的斜率表示物体速度的大小和方向,而v-t图像的斜率表示物体加速度的大小和方向。
【变式训练2】 (多选)下图是甲、乙、丙、丁、戊五个运动物体相对同一原点的位移—时间图像。下面有关说法正确的是( )
(a)
(b)
(c)
A.甲、乙运动的出发点相距x0 B.乙比甲早出发t1的时间
C.丙在0~2 s内,物体的位移大于2 m D.丁、戊两物体在25 s时相遇
答案:AD
解析:由图可知,乙从原点出发,甲从距原点x0处出发,则两物体的出发点相距x0,故A正确;甲在t=0时刻开始运动,而乙在t1时刻开始运动,则甲比乙早出发t1时间,故B错误;丙在0~2 s内,物体的位移为Δx=0-0=0,故C错误;丁、戊两物体在25 s时到达同位置而相遇,故D正确。
【问题引领】
只能用位移公式求匀变速直线运动的位移吗
提示:不。可以灵活运用各种不同的关系和方法求匀变速直线运动的位移。如用平均速度、运动图像、比例关系等。
【归纳提升】
1.平均速度
(1)结论:做匀变速直线运动的物体,在一段时间t内的平均速度等于这段时间内中间时刻的瞬时速度,还等于这段时间初末速度矢量和的一半。
(2)推导:设物体的初速度为v0,做匀变速直线运动的加速度为a,t末的速度为vt。
2.逐差相等
(1)结论:在任意两个连续相等的时间间隔T内,位移之差是一个常量,即Δx=xⅡ-xⅠ=aT2。
注意:则xⅠ=x1,xⅡ=x2-x1 ③
由①②③得Δx=xⅡ-xⅠ=aT2。
公式Δx=aT2的应用:一是用以判断物体是否做匀变速直线运动,二是用以求加速度。
【典型例题】
【例题3】 从车站开出的汽车,做匀加速直线运动,走了12 s后发现,还有乘客没上来,于是立即做匀减速直线运动至停车,共历时20 s,行进50 m,求其最大速度。
答案:5 m/s
解析:法一(基本公式法) 设最大速度为vmax,由题意得
【变式训练3】 如图所示,一小球(可视为质点)沿斜面匀加速下滑,依次经过A、B、C三点。已知xAB=18 m,xBC=30 m,小球经过AB和BC两段所用的时间均为2 s,则小球经过A、B、C三点时的速度大小分别是( )
A.12 m/s,13 m/s,14 m/s B.10 m/s,14 m/s,18 m/s
C.8 m/s,10 m/s,16 m/s D.6 m/s,12 m/s,18 m/s
答案:D
A.加速度大的物体位移大
B.初速度大的物体位移大
C.末速度大的物体位移大
D.以上说法都不对
答案:D
解析:由 知,x的大小与初速度、加速度、时间都有关,t一定时,x与两个量有关,不能简单地说初速度大或加速度大,位移一定大,A、B、C均错,D对。
2.(x-t图像)下列图像均能正确反映物体在直线上的运动,在t=2 s内物体位移最大的是( )
答案:B
解析:选项A、C、D中2 s内物体位移均为0,选项B中物体一直向正方向运动,B正确。
3.(x-t图像)(多选)下图为在同一直线上运动的A、B两质点的x-t图像,由图可知( )
A.t=0时,A在B的前面
B.B在t2时刻追上A,并在此后运动到A的前面
C.B开始运动的速度比A的小,t2时刻后才大于A的速度
D.A运动的速度始终比B的大
答案:AB
解析:t=0时,A在原点正方向x1位置处,B在原点处,A在B的前面,A对。t2时刻两图线相交,表示该时刻B追上A,并在此后运动到A的前面,B对。B开始运动的速度比A的小,t1时刻后A静止,B仍然运动,C、D错。
4.(刹车类问题)汽车以20 m/s的速度做匀速直线运动,刹车后的加速度大小为5 m/s2,那么开始刹车后2 s内与开始刹车后6 s内汽车通过的位移之比为
( )
A.1∶1 B.1∶3
C.3∶4 D.4∶3
答案:C
5.(匀变速直线运动基本公式的应用)一物体做初速度为零的匀加速直线运动,加速度为a=2 m/s2,求:
(1)第5 s末物体的速度多大
(2)前4 s的位移多大
(3)第4 s内的位移多大
答案:(1)10 m/s (2)16 m (3)7 m
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
