2023-2024学年冀教版九年级上学期数学26.1.2锐角三角函数 课件(共20张PPT)
文档属性
| 名称 | 2023-2024学年冀教版九年级上学期数学26.1.2锐角三角函数 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 308.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
冀教版
九年级上册
第二十六章 解直角三角形
26.1.2锐角三角函数
01. 类比正切,经历探究正弦、余弦概念的过程.
学习
目标
02. 能独立计算特殊角的正弦、余弦值,发展推理能力.
03. 能够根据直角三角形中的边角关系,进行简单的计算,提高计算能力和逻辑思维能力.
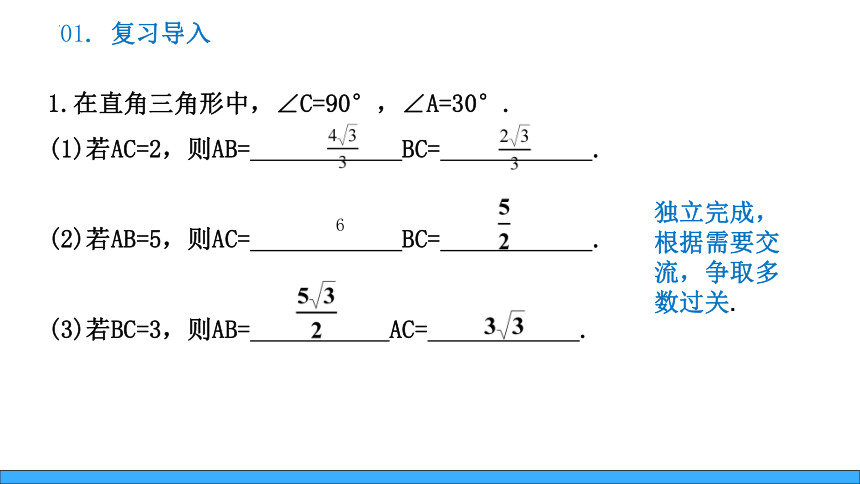
1.在直角三角形中,∠C=90°,∠A=30°.
(1)若AC=2,则AB= BC= .
(2)若AB=5,则AC= BC= .
(3)若BC=3,则AB= AC= .
01. 复习导入
6
独立完成,根据需要交流,争取多数过关.
01. 复习导入
2. 在直角三角形中,∠C=90°,∠A=45°.
(1)若AC=2,则AB= BC= .
(2)若AB=6,求AC= BC= .
2
独立完成,根据需要交流,争取多数过关.
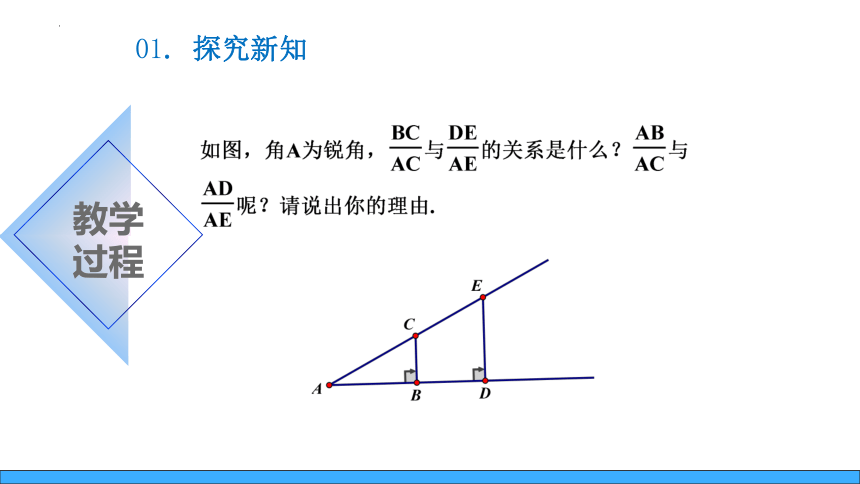
01. 探究新知
教学
过程
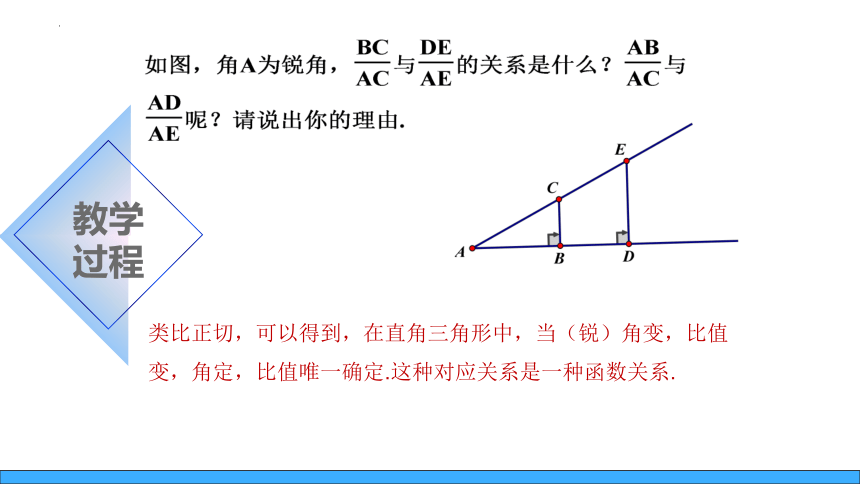
教学
过程
类比正切,可以得到,在直角三角形中,当(锐)角变,比值变,角定,比值唯一确定.这种对应关系是一种函数关系.
在Rt△ABC中,∠C=90°,∠A对边和斜边的比叫做∠A的正弦,记作sinA,即
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
我们把锐角A的正弦、余弦和正切统称为A的三角函数.
01. 概念建立
1.在锐角三角函数中,谁是自变量、谁是自变量的函数呢?
锐角是自变量,比值即正弦、余弦、正切是自变量的函数.
我们把锐角A的正弦、余弦和正切统称为A的三角函数.
01. 概念建立
2. 你能根据定义,分别求出正弦、余弦、正切的范围呢?
0<sinA<1 0<cosA<1 tanA>0
请利用特殊三角形三边关系以及三角函数定义,小组合作完成下面表格.
02. 特殊角三角函数探究
A 30° 45° 60°
sinA
cosA
tanA
例2 求下列各式的值:
(1)2sin30°+3tan30°-tan45°
(2)(sin45°) +tan60°sin60°
03. 运用新知
例3 如图,在Rt△ABC中,∠ACD=90°,AC=5,BC=12,CD⊥AB,垂足为D.
求sinB、cosB、tanB、sin∠ACD的值.
转化求
1.求下列各式的值:
(1)2cos60°+3tan30°
(2)sin 60°+tan60°cos30°
04. 课堂练习
04. 课堂练习
解:如图CosA=
∴AB=9
在直角三角形ABC中
有勾股定理可得BC=3
拓展提高
解:如图,过点A做AD垂直于BC于点D
∵AB=AC=5,BC=6
∴BD=4
在直角三角形ABD中,可得AD=4
∴
3.在等腰三角形ABC中,AB=AC=5,BC=6,求∠B的三个三角函数值.
4 如图,△ABC 的顶点是正方形网格的格点,则sin A 的值为( )
A. B.
C. D.
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α 的值是( )
A. B.
C. D.
C
5
B
课堂
小结
作业设计方案:
基础性作业(必做):课后习题A组1、2题.
拓展性作业(选做):课后习题B组任选1题.
感谢聆听
冀教版
九年级上册
第二十六章 解直角三角形
26.1.2锐角三角函数
01. 类比正切,经历探究正弦、余弦概念的过程.
学习
目标
02. 能独立计算特殊角的正弦、余弦值,发展推理能力.
03. 能够根据直角三角形中的边角关系,进行简单的计算,提高计算能力和逻辑思维能力.
1.在直角三角形中,∠C=90°,∠A=30°.
(1)若AC=2,则AB= BC= .
(2)若AB=5,则AC= BC= .
(3)若BC=3,则AB= AC= .
01. 复习导入
6
独立完成,根据需要交流,争取多数过关.
01. 复习导入
2. 在直角三角形中,∠C=90°,∠A=45°.
(1)若AC=2,则AB= BC= .
(2)若AB=6,求AC= BC= .
2
独立完成,根据需要交流,争取多数过关.
01. 探究新知
教学
过程
教学
过程
类比正切,可以得到,在直角三角形中,当(锐)角变,比值变,角定,比值唯一确定.这种对应关系是一种函数关系.
在Rt△ABC中,∠C=90°,∠A对边和斜边的比叫做∠A的正弦,记作sinA,即
∠A的邻边与斜边的比叫做∠A的余弦,记作cosA,即
我们把锐角A的正弦、余弦和正切统称为A的三角函数.
01. 概念建立
1.在锐角三角函数中,谁是自变量、谁是自变量的函数呢?
锐角是自变量,比值即正弦、余弦、正切是自变量的函数.
我们把锐角A的正弦、余弦和正切统称为A的三角函数.
01. 概念建立
2. 你能根据定义,分别求出正弦、余弦、正切的范围呢?
0<sinA<1 0<cosA<1 tanA>0
请利用特殊三角形三边关系以及三角函数定义,小组合作完成下面表格.
02. 特殊角三角函数探究
A 30° 45° 60°
sinA
cosA
tanA
例2 求下列各式的值:
(1)2sin30°+3tan30°-tan45°
(2)(sin45°) +tan60°sin60°
03. 运用新知
例3 如图,在Rt△ABC中,∠ACD=90°,AC=5,BC=12,CD⊥AB,垂足为D.
求sinB、cosB、tanB、sin∠ACD的值.
转化求
1.求下列各式的值:
(1)2cos60°+3tan30°
(2)sin 60°+tan60°cos30°
04. 课堂练习
04. 课堂练习
解:如图CosA=
∴AB=9
在直角三角形ABC中
有勾股定理可得BC=3
拓展提高
解:如图,过点A做AD垂直于BC于点D
∵AB=AC=5,BC=6
∴BD=4
在直角三角形ABD中,可得AD=4
∴
3.在等腰三角形ABC中,AB=AC=5,BC=6,求∠B的三个三角函数值.
4 如图,△ABC 的顶点是正方形网格的格点,则sin A 的值为( )
A. B.
C. D.
如图,在平面直角坐标系中,点A的坐标为(3,4),那么sin α 的值是( )
A. B.
C. D.
C
5
B
课堂
小结
作业设计方案:
基础性作业(必做):课后习题A组1、2题.
拓展性作业(选做):课后习题B组任选1题.
感谢聆听
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
