26.1.1锐角三角函数 课件(共19张PPT) 2023-2024学年冀教版九年级上学期数学
文档属性
| 名称 | 26.1.1锐角三角函数 课件(共19张PPT) 2023-2024学年冀教版九年级上学期数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 288.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第二十六章 解直角三角形
26.1.1锐角三角函数
冀教版
九年级上册
教学
目标
01. 经历从实际问题中抽象出数学模型
的过程,发展学生数学抽象能力.
02. 探索直角三角形中边角关系,经历正切概念建立的过程.
03. 探索30°、45°、60°正切值的过程,并能进行简单的计算.
01. 情景导入
教学
过程
如图26-1-1,轮船在 A 处时,灯塔 B 位于它的北偏东35°的方向上,轮船向东航行5 km 到达 C 处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?(结果保留两位小数)
事实上,本题就是在 Rt △ABC 中,已知 ∠C =90°, ∠BAC =55, AC =5 km ,求 BC 长度的问题,换句话说,在直角三角形中,已知一个锐角及它的邻边,求它对边的问题.
解决此问题,需要学习直角三角形边角关系.
01. 情景导入
教学
过程
如图26-1-1,轮船在 A 处时,灯塔 B 位于它的北偏东35°的方向上,轮船向东航行5 km 到达 C 处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?(结果保留两位小数)
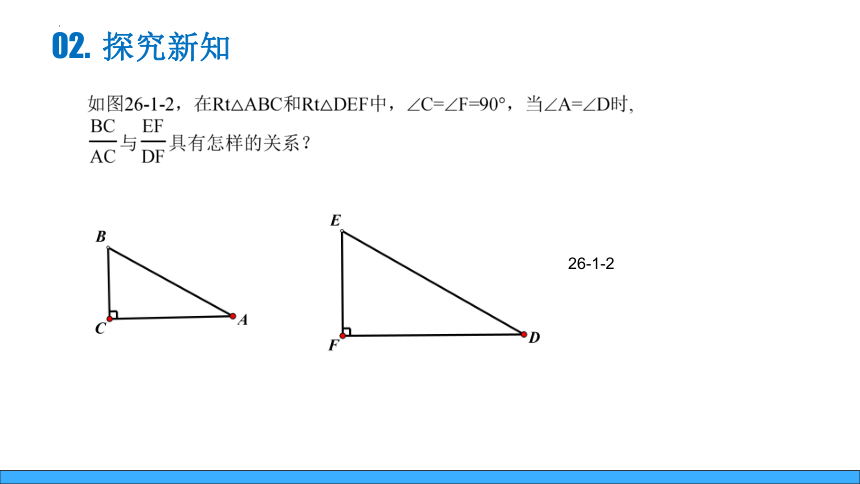
02. 探究新知
26-1-2
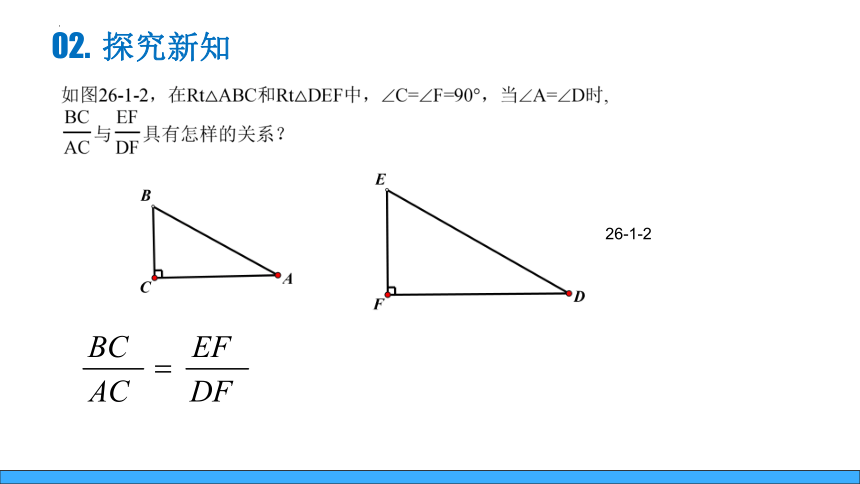
02. 探究新知
26-1-2
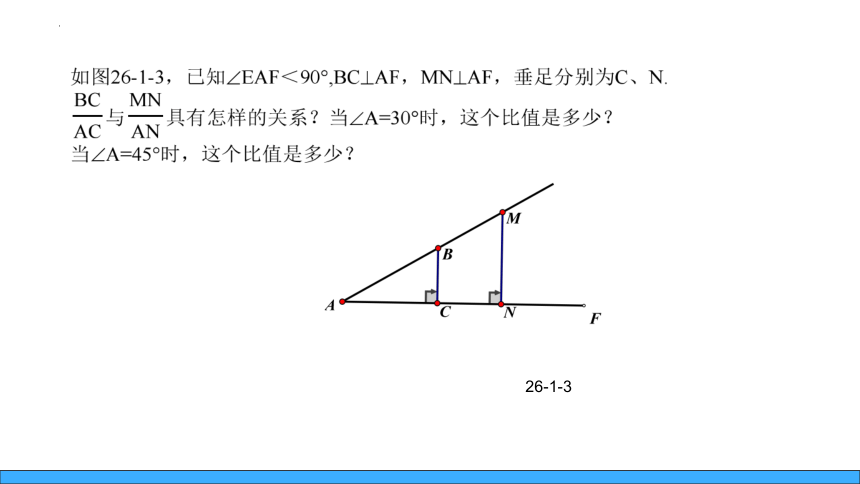
26-1-3
26-1-3
当∠A=30°时,这个比值为
当∠A=45°时,这个比值为1
26-1-3
你能从中得出怎样的认识?
在直角三角形中,当一个锐角确定时,它的两个直角边的比值随之确定。
02. 概念建立
在直角三角形ABC,∠C=90°,我们把∠A的对边与邻边的比值,叫做∠A的正切,记作tanA,即
∠B的对边、邻边分别是?
02. 概念建立
在直角三角形ABC,∠C=90°,我们把∠A的对边与邻边的比值,叫做∠A的正切,记作tanA,即
如上图,tanA= tanB= 它们的关系是什么?
03. 特殊角正切值探究
1.在Rt△ABC中,∠C=90°,∠A=30°则BC:AC:AB= .
2.在Rt△ABC中,∠C=90°,∠A=45°则BC:AC:AB= .
03. 特殊角正切值探究
3.请你根据特殊三角形三边关系以及正切的定义填空:tan30°= . tan45°= . tan60°= .
04. 课堂检测
1.求下列各式的值:
(1)tan60°× tan30° (2)2tan45° +3tan30°
2.在Rt△ABC中,∠C=90°,AB=9,BC=5,求tanB的值.
04. 课堂检测
2.在Rt△ABC中,∠C=90°,AB=9,BC=5,求tanB的值.
解:∵在Rt△ABC中,∠C=90°,AB=9,BC=5,
有勾股定理可得
AC=
∴tanB=
04. 课堂检测
3.在直角三角形中,斜边为8,一条直角边为 ,这条直角边
所对 锐角为A,求tanA的值
解:设如图AB=8,BC=
求tanA的值
在Rt△ABC中,∠C=90°有勾股定理可得
AC=
∴tanA=
∴
课堂
小结
作业设计方案:
基础性作业(必做):课后习题A组1、2题.
拓展性作业(选做):课后习题B组任选1题.
感谢聆听
第二十六章 解直角三角形
26.1.1锐角三角函数
冀教版
九年级上册
教学
目标
01. 经历从实际问题中抽象出数学模型
的过程,发展学生数学抽象能力.
02. 探索直角三角形中边角关系,经历正切概念建立的过程.
03. 探索30°、45°、60°正切值的过程,并能进行简单的计算.
01. 情景导入
教学
过程
如图26-1-1,轮船在 A 处时,灯塔 B 位于它的北偏东35°的方向上,轮船向东航行5 km 到达 C 处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?(结果保留两位小数)
事实上,本题就是在 Rt △ABC 中,已知 ∠C =90°, ∠BAC =55, AC =5 km ,求 BC 长度的问题,换句话说,在直角三角形中,已知一个锐角及它的邻边,求它对边的问题.
解决此问题,需要学习直角三角形边角关系.
01. 情景导入
教学
过程
如图26-1-1,轮船在 A 处时,灯塔 B 位于它的北偏东35°的方向上,轮船向东航行5 km 到达 C 处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?(结果保留两位小数)
02. 探究新知
26-1-2
02. 探究新知
26-1-2
26-1-3
26-1-3
当∠A=30°时,这个比值为
当∠A=45°时,这个比值为1
26-1-3
你能从中得出怎样的认识?
在直角三角形中,当一个锐角确定时,它的两个直角边的比值随之确定。
02. 概念建立
在直角三角形ABC,∠C=90°,我们把∠A的对边与邻边的比值,叫做∠A的正切,记作tanA,即
∠B的对边、邻边分别是?
02. 概念建立
在直角三角形ABC,∠C=90°,我们把∠A的对边与邻边的比值,叫做∠A的正切,记作tanA,即
如上图,tanA= tanB= 它们的关系是什么?
03. 特殊角正切值探究
1.在Rt△ABC中,∠C=90°,∠A=30°则BC:AC:AB= .
2.在Rt△ABC中,∠C=90°,∠A=45°则BC:AC:AB= .
03. 特殊角正切值探究
3.请你根据特殊三角形三边关系以及正切的定义填空:tan30°= . tan45°= . tan60°= .
04. 课堂检测
1.求下列各式的值:
(1)tan60°× tan30° (2)2tan45° +3tan30°
2.在Rt△ABC中,∠C=90°,AB=9,BC=5,求tanB的值.
04. 课堂检测
2.在Rt△ABC中,∠C=90°,AB=9,BC=5,求tanB的值.
解:∵在Rt△ABC中,∠C=90°,AB=9,BC=5,
有勾股定理可得
AC=
∴tanB=
04. 课堂检测
3.在直角三角形中,斜边为8,一条直角边为 ,这条直角边
所对 锐角为A,求tanA的值
解:设如图AB=8,BC=
求tanA的值
在Rt△ABC中,∠C=90°有勾股定理可得
AC=
∴tanA=
∴
课堂
小结
作业设计方案:
基础性作业(必做):课后习题A组1、2题.
拓展性作业(选做):课后习题B组任选1题.
感谢聆听
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
