25.6.1相似三角形的应用 课件(共20张PPT)冀教版九年级上学期数学
文档属性
| 名称 | 25.6.1相似三角形的应用 课件(共20张PPT)冀教版九年级上学期数学 |  | |
| 格式 | pptx | ||
| 文件大小 | 849.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 20:21:05 | ||
图片预览





文档简介
(共20张PPT)
第二十五章 图形的相似
25.6.1相似三角形的应用
冀教版
九年级上册
01
02
在解决问题过程中,进一步理解相似三角形的判定和性质.
学习
目标
能够利用相似三角形的知识,求出不能直接测量的物体的高或宽.
能够将实际问题转化为相似三角形的数学模型,提高分析问题、解决问题的能力.
03
01
复习巩固
教学
过程
1.相似三角形的判定方法有哪几种?2.相似三角形的性质有哪些?
02
探究新知
教学
过程
探究1 利用光照下的影子
对于学校里旗杆的高度,我们是无法直接进行测量的.但是我们可以根据相似三角形的知识,测出旗杆的高度.结合下面图形大家思考如何求出高度?
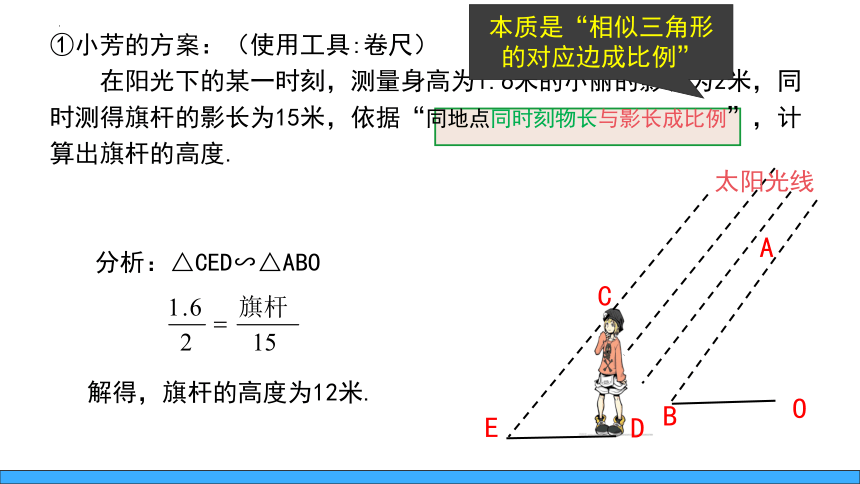
①小芳的方案:(使用工具:卷尺)
在阳光下的某一时刻,测量身高为1.6米的小丽的影长为2米,同时测得旗杆的影长为15米,依据“同地点同时刻物长与影长成比例”,计算出旗杆的高度.
解得,旗杆的高度为12米.
本质是“相似三角形的对应边成比例”
O
A
C
B
E
D
太阳光线
分析:△CED∽△ABO
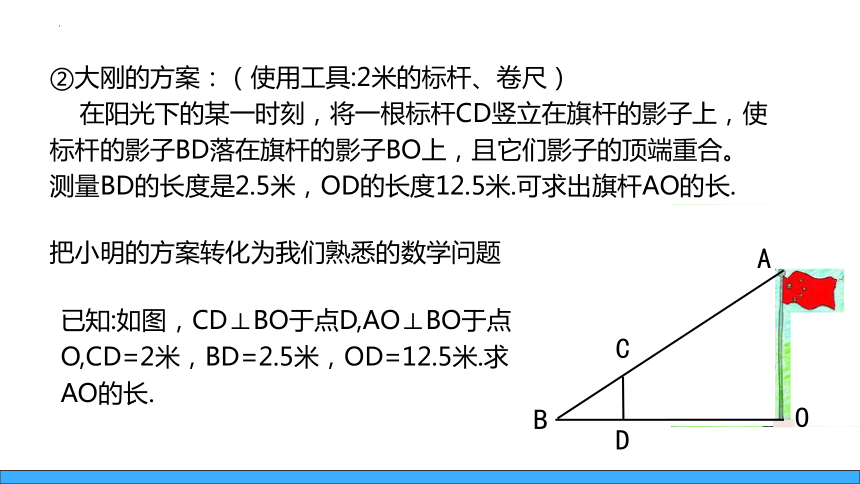
②大刚的方案:(使用工具:2米的标杆、卷尺)
在阳光下的某一时刻,将一根标杆CD竖立在旗杆的影子上,使标杆的影子BD落在旗杆的影子BO上,且它们影子的顶端重合。测量BD的长度是2.5米,OD的长度12.5米.可求出旗杆AO的长.
把小明的方案转化为我们熟悉的数学问题
已知:如图,CD⊥BO于点D,AO⊥BO于点O,CD=2米,BD=2.5米,OD=12.5米.求AO的长.
O
A
D
C
B
O
A
D
C
B
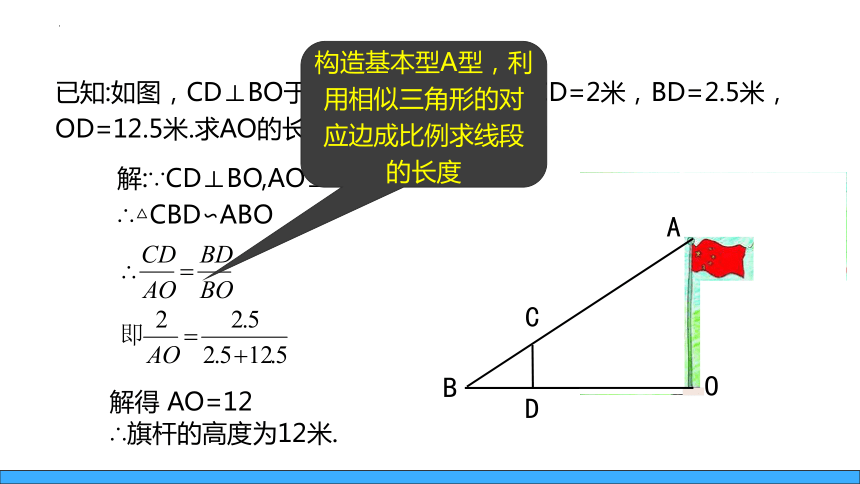
已知:如图,CD⊥BO于点D,AO⊥BO于点O,CD=2米,BD=2.5米,OD=12.5米.求AO的长.
解:∵CD⊥BO,AO⊥BO
∴△CBD∽ABO
解得 AO=12
∴旗杆的高度为12米.
构造基本型A型,利用相似三角形的对应边成比例求线段的长度
运用新知
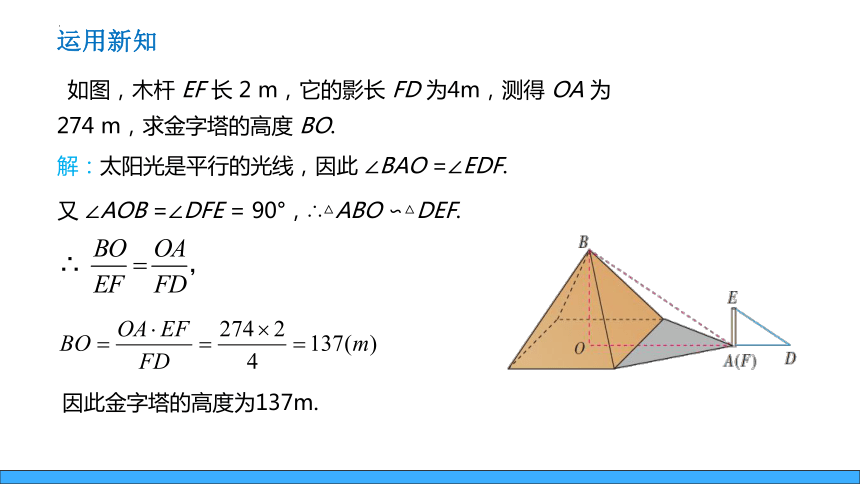
如图,木杆 EF 长 2 m,它的影长 FD 为4m,测得 OA 为 274 m,求金字塔的高度 BO.
解:太阳光是平行的光线,因此 ∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,∴△ABO ∽△DEF.
∴ ,
因此金字塔的高度为137m.
探究2 测量空心圆柱的内径(内径:内部的直径)
有些空心圆柱型的机械零件或容器的内径是不能直接测量的,往往用交叉卡钳进行测量.
A
B
D
C
O
将这个实际问题转化为一个数学问题
如图所示是一个容器,它的外径为a,内径AB未知。现用卡钳去测量,若 ,CD=b,求这个零件的内径为多少?
A
B
D
C
O
∠COD=∠AOB
∴△COD∽△AOB
解得,AB=mb.
∴这个容器的内径是mb.
已知:在△AOB和△COD中, ,CD=b,求AB的长。
A
A'
B
B'
O
将这个实际问题转化为一个数学问题
C
D
探究3 跨学科应用
如图,是“小孔成像”试验示意图.已知蜡烛与光屏之间的距离为 ,具有“小孔”的纸板放在什么位置时,蜡烛火焰的高度AB是它的像A'B'的高度的一半?
A
A'
B
B'
O
C
D
①AB与A'B'的关系是平行
②AB与A'B'的之间的距离是
从题中提取关键信息
③AB是A'B'的一半
探究3 跨学科应用
如图,是“小孔成像”试验示意图.已知蜡烛与光屏之间的距离为 ,具有“小孔”的纸板放在什么位置时,蜡烛火焰的高度AB是它的像A'B'的高度的一半?
A
A'
B
B'
O
C
D
解:过点O作OC⊥AB于点C,延长CO交A'B'于点D
则CD=
∵AB∥A'B'
∴△OAB∽△OA'B'
已知:AB∥A'B',AA'与BB'相交与点O,AB与A'B'之间的距离是 , ,求O到AB的距离.
(相似三角形的对应高的比等于相似比)
03
应用新知
1.小亮和小颖两人准备用测量影子的方法测算其楼高,两人商定用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距离CD=1.25 m,颖颖与楼之间的距离DN=30 m(点C,D,N在一条直线上),颖颖的身高BD=1.6 m,亮亮蹲地观测时眼睛到地面的距离AC=0.8 m.
请你根据以上测量数据帮助他们求出这幢住宅楼的高度.
∵AF∥CN,
∴∠AEB=∠AFM=90°,且∠BAE=∠MAF,
∴△ABE∽△AMF,∴MF(BE)=AF(AE),即MF(1.6-0.8)=1.25+30(1.25),
解得MF=20,∴MN=MF+FN=20+0.8=20.8(m).答:这幢住宅楼的高度为20.8 m.
解:过点A作CN的平行线交BD于点E,交MN于点F.由已知可得FN=ED=AC=0.8 m,
AE=CD=1.25 m,EF=DN=30 m.
2.如图,一位同学想利用树影测量树高AB,他在某一时刻测得高为1米的竹竿影长0.9米,但当他马上测量树影时,因树靠近一幢建筑物,影子不全留在地面上,有一部分影子在墙上CD处,他先测得留在墙上的影高CD为1.2米,又测得地面部分的影长BC为2.7米.则树高AB=_____.
B
A
D
C
4.2米
课堂
小结
知识总结
知识方法要点 关键总结 注意事项
利用相似三角形测高 根据 利用阳光下的影子测高 测量要尽量减少误差,取每种方法计算出的高度的平均 值,可使误差降到最小
方法规律总结
用相似三角形知识解决实际问题时的方法: ① 将实际问题转化为相似三角形问题; ② 构造出一对相似三角形; ③ 根据相似三角形的性质,建立比例式,求出相应的量
作业设计方案
测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.
基础性作业(必做):课后习题1、2题.
拓展性作业(分组实践):
作业设计方案
测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.
以小组为单位对教学楼和校园里大树进行目测与估算,再利用本节课所学知识,选择一种方法对教学楼和校园里大树进行一次较为准确的测算,并写出测量方案,以小组为单位完成一份实践报告
感谢聆听
第二十五章 图形的相似
25.6.1相似三角形的应用
冀教版
九年级上册
01
02
在解决问题过程中,进一步理解相似三角形的判定和性质.
学习
目标
能够利用相似三角形的知识,求出不能直接测量的物体的高或宽.
能够将实际问题转化为相似三角形的数学模型,提高分析问题、解决问题的能力.
03
01
复习巩固
教学
过程
1.相似三角形的判定方法有哪几种?2.相似三角形的性质有哪些?
02
探究新知
教学
过程
探究1 利用光照下的影子
对于学校里旗杆的高度,我们是无法直接进行测量的.但是我们可以根据相似三角形的知识,测出旗杆的高度.结合下面图形大家思考如何求出高度?
①小芳的方案:(使用工具:卷尺)
在阳光下的某一时刻,测量身高为1.6米的小丽的影长为2米,同时测得旗杆的影长为15米,依据“同地点同时刻物长与影长成比例”,计算出旗杆的高度.
解得,旗杆的高度为12米.
本质是“相似三角形的对应边成比例”
O
A
C
B
E
D
太阳光线
分析:△CED∽△ABO
②大刚的方案:(使用工具:2米的标杆、卷尺)
在阳光下的某一时刻,将一根标杆CD竖立在旗杆的影子上,使标杆的影子BD落在旗杆的影子BO上,且它们影子的顶端重合。测量BD的长度是2.5米,OD的长度12.5米.可求出旗杆AO的长.
把小明的方案转化为我们熟悉的数学问题
已知:如图,CD⊥BO于点D,AO⊥BO于点O,CD=2米,BD=2.5米,OD=12.5米.求AO的长.
O
A
D
C
B
O
A
D
C
B
已知:如图,CD⊥BO于点D,AO⊥BO于点O,CD=2米,BD=2.5米,OD=12.5米.求AO的长.
解:∵CD⊥BO,AO⊥BO
∴△CBD∽ABO
解得 AO=12
∴旗杆的高度为12米.
构造基本型A型,利用相似三角形的对应边成比例求线段的长度
运用新知
如图,木杆 EF 长 2 m,它的影长 FD 为4m,测得 OA 为 274 m,求金字塔的高度 BO.
解:太阳光是平行的光线,因此 ∠BAO =∠EDF.
又 ∠AOB =∠DFE = 90°,∴△ABO ∽△DEF.
∴ ,
因此金字塔的高度为137m.
探究2 测量空心圆柱的内径(内径:内部的直径)
有些空心圆柱型的机械零件或容器的内径是不能直接测量的,往往用交叉卡钳进行测量.
A
B
D
C
O
将这个实际问题转化为一个数学问题
如图所示是一个容器,它的外径为a,内径AB未知。现用卡钳去测量,若 ,CD=b,求这个零件的内径为多少?
A
B
D
C
O
∠COD=∠AOB
∴△COD∽△AOB
解得,AB=mb.
∴这个容器的内径是mb.
已知:在△AOB和△COD中, ,CD=b,求AB的长。
A
A'
B
B'
O
将这个实际问题转化为一个数学问题
C
D
探究3 跨学科应用
如图,是“小孔成像”试验示意图.已知蜡烛与光屏之间的距离为 ,具有“小孔”的纸板放在什么位置时,蜡烛火焰的高度AB是它的像A'B'的高度的一半?
A
A'
B
B'
O
C
D
①AB与A'B'的关系是平行
②AB与A'B'的之间的距离是
从题中提取关键信息
③AB是A'B'的一半
探究3 跨学科应用
如图,是“小孔成像”试验示意图.已知蜡烛与光屏之间的距离为 ,具有“小孔”的纸板放在什么位置时,蜡烛火焰的高度AB是它的像A'B'的高度的一半?
A
A'
B
B'
O
C
D
解:过点O作OC⊥AB于点C,延长CO交A'B'于点D
则CD=
∵AB∥A'B'
∴△OAB∽△OA'B'
已知:AB∥A'B',AA'与BB'相交与点O,AB与A'B'之间的距离是 , ,求O到AB的距离.
(相似三角形的对应高的比等于相似比)
03
应用新知
1.小亮和小颖两人准备用测量影子的方法测算其楼高,两人商定用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D,然后测出两人之间的距离CD=1.25 m,颖颖与楼之间的距离DN=30 m(点C,D,N在一条直线上),颖颖的身高BD=1.6 m,亮亮蹲地观测时眼睛到地面的距离AC=0.8 m.
请你根据以上测量数据帮助他们求出这幢住宅楼的高度.
∵AF∥CN,
∴∠AEB=∠AFM=90°,且∠BAE=∠MAF,
∴△ABE∽△AMF,∴MF(BE)=AF(AE),即MF(1.6-0.8)=1.25+30(1.25),
解得MF=20,∴MN=MF+FN=20+0.8=20.8(m).答:这幢住宅楼的高度为20.8 m.
解:过点A作CN的平行线交BD于点E,交MN于点F.由已知可得FN=ED=AC=0.8 m,
AE=CD=1.25 m,EF=DN=30 m.
2.如图,一位同学想利用树影测量树高AB,他在某一时刻测得高为1米的竹竿影长0.9米,但当他马上测量树影时,因树靠近一幢建筑物,影子不全留在地面上,有一部分影子在墙上CD处,他先测得留在墙上的影高CD为1.2米,又测得地面部分的影长BC为2.7米.则树高AB=_____.
B
A
D
C
4.2米
课堂
小结
知识总结
知识方法要点 关键总结 注意事项
利用相似三角形测高 根据 利用阳光下的影子测高 测量要尽量减少误差,取每种方法计算出的高度的平均 值,可使误差降到最小
方法规律总结
用相似三角形知识解决实际问题时的方法: ① 将实际问题转化为相似三角形问题; ② 构造出一对相似三角形; ③ 根据相似三角形的性质,建立比例式,求出相应的量
作业设计方案
测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.
基础性作业(必做):课后习题1、2题.
拓展性作业(分组实践):
作业设计方案
测量方法:测量不能到达顶部的物体的高度时,常常利用光线构造相似三角形(如同一时刻,物高与影长)来解决.常见的测量方式有四种,如图所示.
以小组为单位对教学楼和校园里大树进行目测与估算,再利用本节课所学知识,选择一种方法对教学楼和校园里大树进行一次较为准确的测算,并写出测量方案,以小组为单位完成一份实践报告
感谢聆听
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
