第3章 一元一次方程复习课件(共45张PPT) 人教版七年级数学上册
文档属性
| 名称 | 第3章 一元一次方程复习课件(共45张PPT) 人教版七年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 603.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 18:27:14 | ||
图片预览






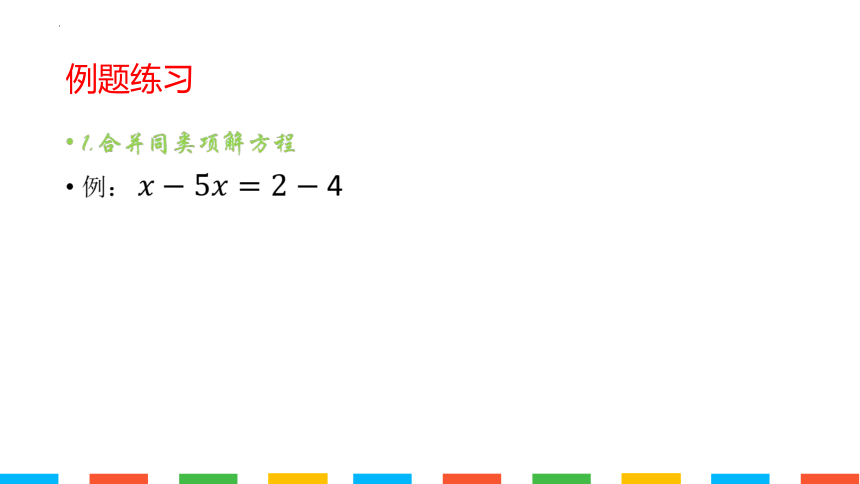

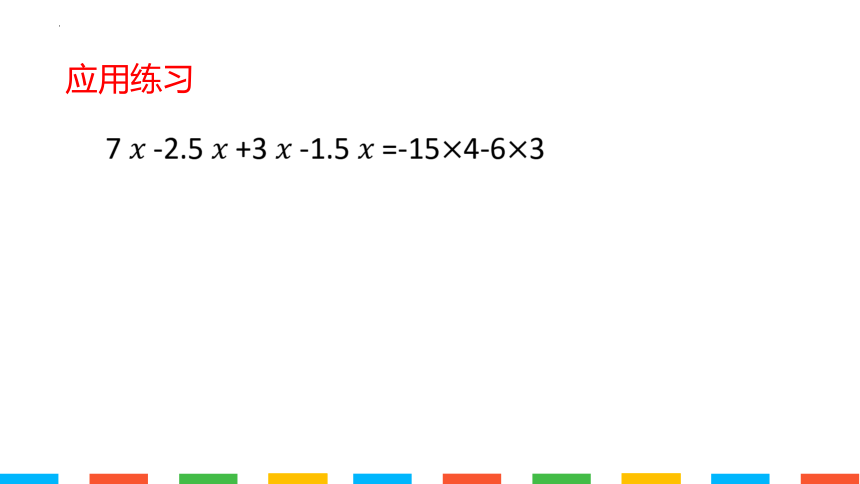


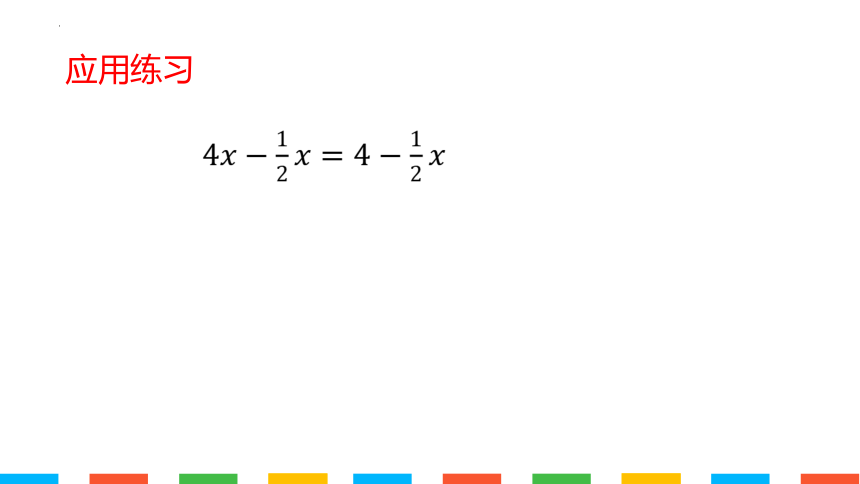
文档简介
(共45张PPT)
一元一次方程
课程目标
什么是一元一次方程
解方程:合并同类项与移项
去括号与去分母
用一元一次方程解决实际问题
知识讲解
一元一次方程
用一根长24的铁丝围成一个正方形,正方形的边长是多少?
方程就是含有未知数的等式,各方程中都只含有一个未知数,未知数的次数都是1,等号两边都是整式,这样的方程叫做一元一次方程。
解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解。
知识讲解
等式的性质
1.等式两边加(或减)同一个数(或式子),结果仍相等。
2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
知识讲解
利用等式的性质解方程
1. +7=26 2. -5 =20 3. -5=4
例题练习
1.合并同类项解方程
例: 4
例题练习
- 2= 5 - 3
应用练习
7 -2.5 +3 -1.5 =-154-63
应用练习
移项解一元一次方程
例
例题练习
应用练习
应用练习
应用练习
3b61
3.去括号解一元一次方程
例题练习
应用练习
应用练习
应用练习
4.去分母解一元一次方程
例题练习
应用练习
应用练习
应用练习
应用练习
应用练习
一元一次方程的应用
一元一次方程应用问题解题步骤:
审:审清题意,找出题中的数量关系,分析题中的已知量和未知量。
设:设未知数,用未知数表示其他未知量。
列:根据题中的相等关系,列出一元一次方程。
解:解所列出的一元一次方程。
验:检验所得的解是否符合题意。
答:写出答案(包括单位名称)。
知识讲解
1.打折销售问题
与打折销售有关的概念
①成本:即进价,商品进货时的价格;
②标价(原价):在商店出售时所标明的价格;
③实际售价:商品出手时的实际价格;
④利润:商品的纯收入,即实际售价高出成本;
⑤利润率:商品的利润与成本价的比值;
⑥打折:打几折后的价钱就是标价乘十分之几;
知识讲解
与打折销售有关的公式:
①利润=售价-成本价(进价);
②利润率=;
③售价=成本+利润=成本价×(1+利润率)
④售价=标价×打折数
知识讲解
一个书包的标价为元,按折出售仍可获利,该书包的进价为________元.
例题练习
应用练习
若一件商品按成本价提高后标价,又以折优惠卖出,结果仍可获利元,则这件商品的成本价为________元.
应用练习
小张的服装店在换季时积压了一批同一款式的服装,为了缓解资金压力,小张决定打折销售,若每件服装按标价的折出售,将亏元,而按标价的折出售,将赚元.则每件服装的标价是________元.
应用练习
某商店以固定进价一次性购进一种商品,月份按一定售价销售,销售额为元,为扩大销量,减少库存,月份在月份售价基础上打折销售,结果销售量增加件,销售额增加元.
(1)求该商店月份这种商品的售价是多少元?
应用练习
2.行程问题
相遇问题
知识讲解
同时出发(两段):
不同时出发(三段):
例题练习
甲、乙两站相距360千米,一列慢车从甲站开出,每小时行50千米,一列快车从乙站开出,每小时行79千米,两车同时开出,相向而行,多长时间相遇?
应用练习
两地相距1320千米,一列火车从甲地开出,每小时48千米;另一列火车从乙地开出,每小时行72千米,两列火车同时开出,相向而行,经几小时相遇?
应用练习
A、B两地相距60千米,甲、乙两人同时从A、B两地骑自行车出发,相向而行,甲每小时比乙多行2千米,经过2小时相遇,问甲、乙两人的速度分别是多少?
追及问题
同向而行:
同地不同时:慢车先行路程+慢车后行路程=快车路程
同时不同地:快车路程=慢车路程+相距距离
不同时不同地:
①快车先行路程+快车后行路程=慢车路程+相距距离
②慢车先行路程+慢车后行路程+相距距离=快车路程
知识讲解
例题讲解
A、B两地相距600千米,甲车以60km/h的速度从A地驶向B地,2h后,乙车以100km/h的速度沿着相同的道路从A地驶向B地,设乙车出发x小时后追上甲车,根据题意可列方程为( )
应用练习
小明、小亮两人练习赛跑,小明每秒跑4m,小亮每秒跑4.5m,小明先跑6m后小亮开始跑,设小亮跑了x秒后追上小明,依题意可列方程为___________。
应用练习
敌我两军相距25千米,敌军以每小时5千米的速度逃跑,我军同时以每小时8千米的速度去追,并在相距1千米处发生战斗,问战斗是在开始追去几小时后发生的?
应用练习
一队学生去郊外参加公益活动,以4千米/时的速度步行前往,学生出发1.5小时后,学校有紧急通知要传给学生,通讯员从学校出发,骑摩托车以28千米/时的速度沿原路追上去,通讯员要多少分钟才能追上学生的队伍?
应用练习
几名同学约好一起去动物园,到学校集合后,一部分同学以每小时5千米的速度步行,0.5小时后,另一部分同学骑自行车上学,20分钟后,他们同时到达动物园,骑自行车的同学的速度是多少?
流水行船
基本公式:
顺水速度=船速+水速
水速=顺水速度-船速
船速=顺水速度-水速
逆水速度=船速-水速
水速=船速-逆水速度
船速=(顺水速度+逆水速度)÷2
水速=(顺水速度—逆水速度)÷2
解题关键
顺流路程=逆流路程
顺水速度×顺水时间=逆水速度×逆水时间
例题练习
一艘船从甲码头到乙码头顺流而行,用了3小时,从乙码头返回甲码头逆流而上,多用了1.5小时,已知水流的速度是4km/h,设船在静水中的平均速度为xkm/h,可列方程为_______。
应用练习
一架飞机在两城之间飞行,顺风需要4小时,逆风需要4.5小时;测得风速为45千米/时,求两城之间的距离。
应用练习
一船由甲地开往乙地,顺水航行要4小时,逆水航行比顺水航行多用40分钟,已知船在静水中的速度为16千米/时,求水流速度。设水流速度为x千米/时,列方程为_______。
一元一次方程
课程目标
什么是一元一次方程
解方程:合并同类项与移项
去括号与去分母
用一元一次方程解决实际问题
知识讲解
一元一次方程
用一根长24的铁丝围成一个正方形,正方形的边长是多少?
方程就是含有未知数的等式,各方程中都只含有一个未知数,未知数的次数都是1,等号两边都是整式,这样的方程叫做一元一次方程。
解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解。
知识讲解
等式的性质
1.等式两边加(或减)同一个数(或式子),结果仍相等。
2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
知识讲解
利用等式的性质解方程
1. +7=26 2. -5 =20 3. -5=4
例题练习
1.合并同类项解方程
例: 4
例题练习
- 2= 5 - 3
应用练习
7 -2.5 +3 -1.5 =-154-63
应用练习
移项解一元一次方程
例
例题练习
应用练习
应用练习
应用练习
3b61
3.去括号解一元一次方程
例题练习
应用练习
应用练习
应用练习
4.去分母解一元一次方程
例题练习
应用练习
应用练习
应用练习
应用练习
应用练习
一元一次方程的应用
一元一次方程应用问题解题步骤:
审:审清题意,找出题中的数量关系,分析题中的已知量和未知量。
设:设未知数,用未知数表示其他未知量。
列:根据题中的相等关系,列出一元一次方程。
解:解所列出的一元一次方程。
验:检验所得的解是否符合题意。
答:写出答案(包括单位名称)。
知识讲解
1.打折销售问题
与打折销售有关的概念
①成本:即进价,商品进货时的价格;
②标价(原价):在商店出售时所标明的价格;
③实际售价:商品出手时的实际价格;
④利润:商品的纯收入,即实际售价高出成本;
⑤利润率:商品的利润与成本价的比值;
⑥打折:打几折后的价钱就是标价乘十分之几;
知识讲解
与打折销售有关的公式:
①利润=售价-成本价(进价);
②利润率=;
③售价=成本+利润=成本价×(1+利润率)
④售价=标价×打折数
知识讲解
一个书包的标价为元,按折出售仍可获利,该书包的进价为________元.
例题练习
应用练习
若一件商品按成本价提高后标价,又以折优惠卖出,结果仍可获利元,则这件商品的成本价为________元.
应用练习
小张的服装店在换季时积压了一批同一款式的服装,为了缓解资金压力,小张决定打折销售,若每件服装按标价的折出售,将亏元,而按标价的折出售,将赚元.则每件服装的标价是________元.
应用练习
某商店以固定进价一次性购进一种商品,月份按一定售价销售,销售额为元,为扩大销量,减少库存,月份在月份售价基础上打折销售,结果销售量增加件,销售额增加元.
(1)求该商店月份这种商品的售价是多少元?
应用练习
2.行程问题
相遇问题
知识讲解
同时出发(两段):
不同时出发(三段):
例题练习
甲、乙两站相距360千米,一列慢车从甲站开出,每小时行50千米,一列快车从乙站开出,每小时行79千米,两车同时开出,相向而行,多长时间相遇?
应用练习
两地相距1320千米,一列火车从甲地开出,每小时48千米;另一列火车从乙地开出,每小时行72千米,两列火车同时开出,相向而行,经几小时相遇?
应用练习
A、B两地相距60千米,甲、乙两人同时从A、B两地骑自行车出发,相向而行,甲每小时比乙多行2千米,经过2小时相遇,问甲、乙两人的速度分别是多少?
追及问题
同向而行:
同地不同时:慢车先行路程+慢车后行路程=快车路程
同时不同地:快车路程=慢车路程+相距距离
不同时不同地:
①快车先行路程+快车后行路程=慢车路程+相距距离
②慢车先行路程+慢车后行路程+相距距离=快车路程
知识讲解
例题讲解
A、B两地相距600千米,甲车以60km/h的速度从A地驶向B地,2h后,乙车以100km/h的速度沿着相同的道路从A地驶向B地,设乙车出发x小时后追上甲车,根据题意可列方程为( )
应用练习
小明、小亮两人练习赛跑,小明每秒跑4m,小亮每秒跑4.5m,小明先跑6m后小亮开始跑,设小亮跑了x秒后追上小明,依题意可列方程为___________。
应用练习
敌我两军相距25千米,敌军以每小时5千米的速度逃跑,我军同时以每小时8千米的速度去追,并在相距1千米处发生战斗,问战斗是在开始追去几小时后发生的?
应用练习
一队学生去郊外参加公益活动,以4千米/时的速度步行前往,学生出发1.5小时后,学校有紧急通知要传给学生,通讯员从学校出发,骑摩托车以28千米/时的速度沿原路追上去,通讯员要多少分钟才能追上学生的队伍?
应用练习
几名同学约好一起去动物园,到学校集合后,一部分同学以每小时5千米的速度步行,0.5小时后,另一部分同学骑自行车上学,20分钟后,他们同时到达动物园,骑自行车的同学的速度是多少?
流水行船
基本公式:
顺水速度=船速+水速
水速=顺水速度-船速
船速=顺水速度-水速
逆水速度=船速-水速
水速=船速-逆水速度
船速=(顺水速度+逆水速度)÷2
水速=(顺水速度—逆水速度)÷2
解题关键
顺流路程=逆流路程
顺水速度×顺水时间=逆水速度×逆水时间
例题练习
一艘船从甲码头到乙码头顺流而行,用了3小时,从乙码头返回甲码头逆流而上,多用了1.5小时,已知水流的速度是4km/h,设船在静水中的平均速度为xkm/h,可列方程为_______。
应用练习
一架飞机在两城之间飞行,顺风需要4小时,逆风需要4.5小时;测得风速为45千米/时,求两城之间的距离。
应用练习
一船由甲地开往乙地,顺水航行要4小时,逆水航行比顺水航行多用40分钟,已知船在静水中的速度为16千米/时,求水流速度。设水流速度为x千米/时,列方程为_______。
