数学北师大版 八年级下册第一章 三角形的证明:1.3《线段的垂直平分线》优秀教学课件 23张PPT
文档属性
| 名称 | 数学北师大版 八年级下册第一章 三角形的证明:1.3《线段的垂直平分线》优秀教学课件 23张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 932.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第一章 第三节
线段的垂直平分线
知识要点
知识点一
知识点二
知识点一 线段的垂直平分线的性质
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
拓展归纳
理解线段的垂直平分线性质的要点:
(1)这里的线段垂直平分线上的点是指该直线上任意一点.
(2)这里的距离是指线段垂直平分线上的点与线段两个端点间线段的长度.
知识点一
知识点二
知识要点
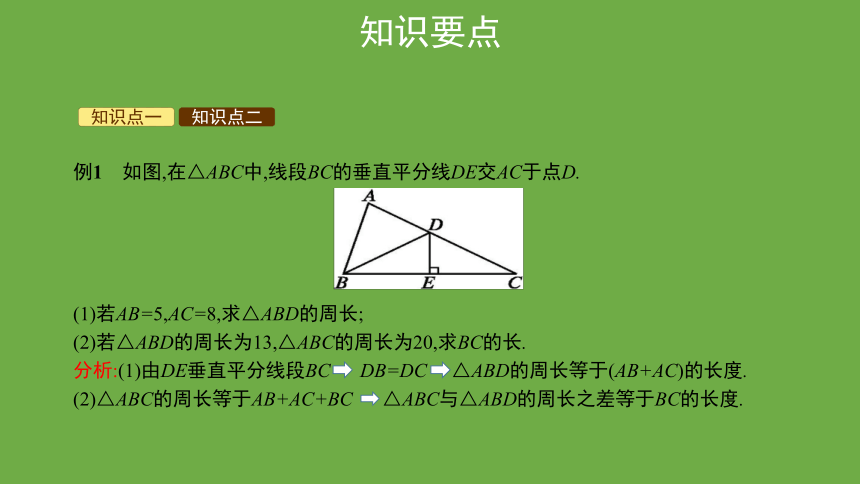
例1 如图,在△ABC中,线段BC的垂直平分线DE交AC于点D.
(1)若AB=5,AC=8,求△ABD的周长;
(2)若△ABD的周长为13,△ABC的周长为20,求BC的长.
分析:(1)由DE垂直平分线段BC DB=DC △ABD的周长等于(AB+AC)的长度.
(2)△ABC的周长等于AB+AC+BC △ABC与△ABD的周长之差等于BC的长度.
知识点一
知识点二
知识要点
解:(1)∵DE是BC的垂直平分线,
∴DB=DC(线段垂直平分线上的点到这条线段两个端点的距离相等).
∴△ABD的周长为AB+BD+AD=AB+CD+AD=AB+AC=13.
(2)由(1)知△ABD的周长等于(AB+AC)的长度.
∵△ABC的周长为(AB+AC+BC)的长度,
∴BC等于△ABC的周长与△ABD的周长之差,即BC=20-13=7.
知识要点
知识点一
知识点二
知识点二 线段的垂直平分线的判定
定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
拓展归纳
(1)判定一条直线是线段的垂直平分线必须说明该直线上有两个点到线段两个端点的距离相等.
(2)线段垂直平分线的判定与性质是题设与结论互换的两个命题.线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.
知识要点
知识点一
知识点二
例2 如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:AD垂直平分EF.
分析:要证AD垂直平分EF,即证A,D分别在EF的垂直平分线上,即证AE=AF,DE=DF.
证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又AD=AD,∴△AED≌△AFD(AAS).
∴DE=DF,AE=AF.
∴A,D在EF的垂直平分线上(线段垂直平分线的判定定理),即AD垂直平分EF.
知识要点
知识点一
知识点二
拓展延伸
拓展点一
拓展点二
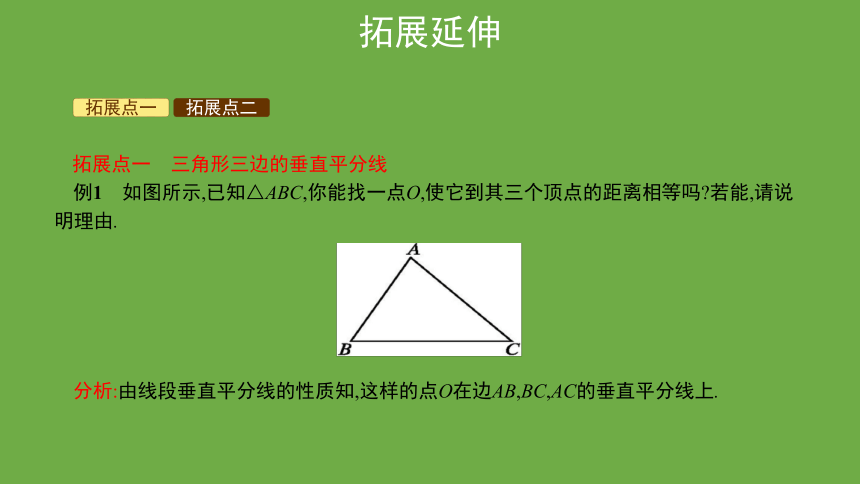
拓展点一 三角形三边的垂直平分线
例1 如图所示,已知△ABC,你能找一点O,使它到其三个顶点的距离相等吗 若能,请说明理由.
分析:由线段垂直平分线的性质知,这样的点O在边AB,BC,AC的垂直平分线上.
拓展点一
拓展点二
拓展延伸
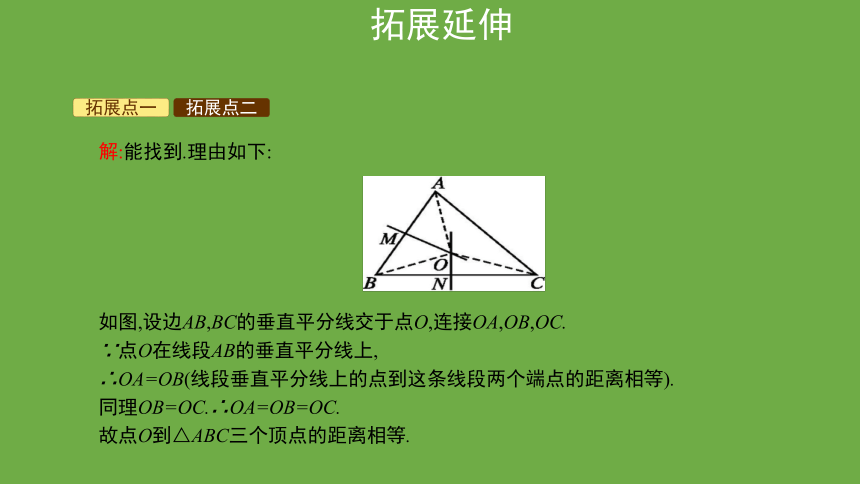
解:能找到.理由如下:
如图,设边AB,BC的垂直平分线交于点O,连接OA,OB,OC.
∵点O在线段AB的垂直平分线上,
∴OA=OB(线段垂直平分线上的点到这条线段两个端点的距离相等).
同理OB=OC.∴OA=OB=OC.
故点O到△ABC三个顶点的距离相等.
拓展点一
拓展点二
拓展延伸
拓展延伸
拓展点一
拓展点二
拓展点二 线段的垂直平分线的有关作图
例2 如图所示,A,B,C三个村庄的干部商议合建一处村民文化活动中心.为了使三个村的村民到该活动中心的距离相等,活动中心应建在什么地方 请用尺规作图的方法在图上找出建活动中心的位置.(不写作法,保留作图痕迹.)
分析:连接三点构成一个三角形,然后作出这个三角形的两边的垂直平分线,相交于一点,该点所在的位置就是所要建活动中心的位置.
拓展延伸
拓展点一
拓展点二
作法:如图所示.
(1)连接AB,BC;
(2)分别作AB,BC的垂直平分线交于点P.
点P所在的位置,即建活动中心的位置.
拓展延伸
拓展点一
拓展点二
思考探究
P22 想一想
答案逆命题:到一条线段两端点距离相等的点,在这条线段的垂直平分线上.这是个真命题.
证明思路,如:已知PA=PB,
(1)过点P作已知线段AB的垂线段PC,再证明点C平分AB;
(2)取AB的中点C,再证明PC⊥AB;
(3)作∠APB的平分线PC,证明PC⊥AB,且AC=BC.
下面给出第(1)种思路的完整证明过程,其他证明过程由同学们自己完成.
已知:如图所示,PA=PB.求证:点P在线段AB的垂直平分线上.
思考探究
证明过点P作PC⊥AB,C为垂足,则∠PCA=∠PCB=90°.
∵PC=PC,PA=PB,
∴Rt△PCA≌Rt△PCB(HL).
∴AC=BC(全等三角形的对应边相等).
∴点P在线段AB的垂直平分线上.
思考探究
P23 问题
答案还有其他证法.
证明∵AB=AC,OB=OC,AO=AO,
∴△AOB≌△AOC(SSS).
∴∠BAO=∠CAO,即AO平分∠BAC.
∴AO垂直平分BC(等腰三角形顶角的角平分线、底边上的中线及底边上的高线互相重合).
P23 随堂练习
证明∵AB是CD的垂直平分线,
∴EC=ED,FC=FD,
∴∠ECD=∠EDC,∠FCD=∠FDC.
∴∠ECD+∠FCD=∠EDC+∠FDC.
∴∠ECF=∠EDF.
习题检测
习题1.7
1.解∵AB=AC,
∵AB的垂直平分线是EF,
∴FA=FB.∴∠B=∠BAF=30°.
∴∠AFC=∠B+∠BAF=30°+30°=60°.
∴∠AFC=60°.
2.解所有顶点都在AB的垂直平分线上(垂足除外).
3.解∵DE垂直平分AB,∴AE=BE.
∵△BEC的周长为BC+BE+EC=50,
∴BC+EC+AE=50,即BC+AC=50.
∵AC=27,∴BC=50-27=23.
习题检测
4.作法:如图,(1)连接AB;
(2)作AB的垂直平分线交河岸于C点,则C点即为所求.
P24 议一议
答案(1)能;无数个;不全等.
(2)能.
P25 做一做
答案能.小明先作了PA=PB,然后作了线段AB的垂直平分线.
习题检测
P26 议一议
作法:1.以P为圆心,以任意长为半径作弧,交直线l于A,B两点.
2.分别以A,B为圆心,以PA的长为半径作弧,两弧交于一点Q.
3.作直线PQ,直线PQ垂直于l.
P26 随堂练习
相等的线段有:AO=BO,AE=BE,AD=DC,AF=FC.
C△AEF=AE+EF+FA=BE+EF+FC=BC=2.
∴△AEF的周长为2.
习题检测
习题1.8
1.已知:线段a.
求作:△ABC,使得AB=AC,BC=a,BC 边上的高AD= a.
作法:如图,(1)作射线BM,在BM上截取BC=a;
(2)作BC的垂直平分线l交BC于D点;
(3)截取AD= a;
(4)连接AB,AC,则△ABC即为所求.
这个等腰三角形是一个等腰直角三角形.
习题检测
2.解(1)如图,过B作AC的垂线,交AC于点O,则BO即为AC边上的高.
(2)延长CB,过A作CB延长线的垂线交延长线于F点.AF即为BC边上的高.
3.提示(1)(2)作△PQR的两边的垂直平分线,其交点即为体育中心G的位置.(3)旨在引发同学们对这一现实问题的进一步思考.实际上,对这类选址问题,从不同角度考虑会有不同的结论.
习题检测
4.解应选方案(3).
为方便起见,不妨设等边△ABC边长为a,
则对于方案(1)有AB+BC=2a;
再见
第一章 第三节
线段的垂直平分线
知识要点
知识点一
知识点二
知识点一 线段的垂直平分线的性质
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
拓展归纳
理解线段的垂直平分线性质的要点:
(1)这里的线段垂直平分线上的点是指该直线上任意一点.
(2)这里的距离是指线段垂直平分线上的点与线段两个端点间线段的长度.
知识点一
知识点二
知识要点
例1 如图,在△ABC中,线段BC的垂直平分线DE交AC于点D.
(1)若AB=5,AC=8,求△ABD的周长;
(2)若△ABD的周长为13,△ABC的周长为20,求BC的长.
分析:(1)由DE垂直平分线段BC DB=DC △ABD的周长等于(AB+AC)的长度.
(2)△ABC的周长等于AB+AC+BC △ABC与△ABD的周长之差等于BC的长度.
知识点一
知识点二
知识要点
解:(1)∵DE是BC的垂直平分线,
∴DB=DC(线段垂直平分线上的点到这条线段两个端点的距离相等).
∴△ABD的周长为AB+BD+AD=AB+CD+AD=AB+AC=13.
(2)由(1)知△ABD的周长等于(AB+AC)的长度.
∵△ABC的周长为(AB+AC+BC)的长度,
∴BC等于△ABC的周长与△ABD的周长之差,即BC=20-13=7.
知识要点
知识点一
知识点二
知识点二 线段的垂直平分线的判定
定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
拓展归纳
(1)判定一条直线是线段的垂直平分线必须说明该直线上有两个点到线段两个端点的距离相等.
(2)线段垂直平分线的判定与性质是题设与结论互换的两个命题.线段的垂直平分线可以看成与线段两个端点距离相等的所有点的集合.
知识要点
知识点一
知识点二
例2 如图所示,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:AD垂直平分EF.
分析:要证AD垂直平分EF,即证A,D分别在EF的垂直平分线上,即证AE=AF,DE=DF.
证明:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又AD=AD,∴△AED≌△AFD(AAS).
∴DE=DF,AE=AF.
∴A,D在EF的垂直平分线上(线段垂直平分线的判定定理),即AD垂直平分EF.
知识要点
知识点一
知识点二
拓展延伸
拓展点一
拓展点二
拓展点一 三角形三边的垂直平分线
例1 如图所示,已知△ABC,你能找一点O,使它到其三个顶点的距离相等吗 若能,请说明理由.
分析:由线段垂直平分线的性质知,这样的点O在边AB,BC,AC的垂直平分线上.
拓展点一
拓展点二
拓展延伸
解:能找到.理由如下:
如图,设边AB,BC的垂直平分线交于点O,连接OA,OB,OC.
∵点O在线段AB的垂直平分线上,
∴OA=OB(线段垂直平分线上的点到这条线段两个端点的距离相等).
同理OB=OC.∴OA=OB=OC.
故点O到△ABC三个顶点的距离相等.
拓展点一
拓展点二
拓展延伸
拓展延伸
拓展点一
拓展点二
拓展点二 线段的垂直平分线的有关作图
例2 如图所示,A,B,C三个村庄的干部商议合建一处村民文化活动中心.为了使三个村的村民到该活动中心的距离相等,活动中心应建在什么地方 请用尺规作图的方法在图上找出建活动中心的位置.(不写作法,保留作图痕迹.)
分析:连接三点构成一个三角形,然后作出这个三角形的两边的垂直平分线,相交于一点,该点所在的位置就是所要建活动中心的位置.
拓展延伸
拓展点一
拓展点二
作法:如图所示.
(1)连接AB,BC;
(2)分别作AB,BC的垂直平分线交于点P.
点P所在的位置,即建活动中心的位置.
拓展延伸
拓展点一
拓展点二
思考探究
P22 想一想
答案逆命题:到一条线段两端点距离相等的点,在这条线段的垂直平分线上.这是个真命题.
证明思路,如:已知PA=PB,
(1)过点P作已知线段AB的垂线段PC,再证明点C平分AB;
(2)取AB的中点C,再证明PC⊥AB;
(3)作∠APB的平分线PC,证明PC⊥AB,且AC=BC.
下面给出第(1)种思路的完整证明过程,其他证明过程由同学们自己完成.
已知:如图所示,PA=PB.求证:点P在线段AB的垂直平分线上.
思考探究
证明过点P作PC⊥AB,C为垂足,则∠PCA=∠PCB=90°.
∵PC=PC,PA=PB,
∴Rt△PCA≌Rt△PCB(HL).
∴AC=BC(全等三角形的对应边相等).
∴点P在线段AB的垂直平分线上.
思考探究
P23 问题
答案还有其他证法.
证明∵AB=AC,OB=OC,AO=AO,
∴△AOB≌△AOC(SSS).
∴∠BAO=∠CAO,即AO平分∠BAC.
∴AO垂直平分BC(等腰三角形顶角的角平分线、底边上的中线及底边上的高线互相重合).
P23 随堂练习
证明∵AB是CD的垂直平分线,
∴EC=ED,FC=FD,
∴∠ECD=∠EDC,∠FCD=∠FDC.
∴∠ECD+∠FCD=∠EDC+∠FDC.
∴∠ECF=∠EDF.
习题检测
习题1.7
1.解∵AB=AC,
∵AB的垂直平分线是EF,
∴FA=FB.∴∠B=∠BAF=30°.
∴∠AFC=∠B+∠BAF=30°+30°=60°.
∴∠AFC=60°.
2.解所有顶点都在AB的垂直平分线上(垂足除外).
3.解∵DE垂直平分AB,∴AE=BE.
∵△BEC的周长为BC+BE+EC=50,
∴BC+EC+AE=50,即BC+AC=50.
∵AC=27,∴BC=50-27=23.
习题检测
4.作法:如图,(1)连接AB;
(2)作AB的垂直平分线交河岸于C点,则C点即为所求.
P24 议一议
答案(1)能;无数个;不全等.
(2)能.
P25 做一做
答案能.小明先作了PA=PB,然后作了线段AB的垂直平分线.
习题检测
P26 议一议
作法:1.以P为圆心,以任意长为半径作弧,交直线l于A,B两点.
2.分别以A,B为圆心,以PA的长为半径作弧,两弧交于一点Q.
3.作直线PQ,直线PQ垂直于l.
P26 随堂练习
相等的线段有:AO=BO,AE=BE,AD=DC,AF=FC.
C△AEF=AE+EF+FA=BE+EF+FC=BC=2.
∴△AEF的周长为2.
习题检测
习题1.8
1.已知:线段a.
求作:△ABC,使得AB=AC,BC=a,BC 边上的高AD= a.
作法:如图,(1)作射线BM,在BM上截取BC=a;
(2)作BC的垂直平分线l交BC于D点;
(3)截取AD= a;
(4)连接AB,AC,则△ABC即为所求.
这个等腰三角形是一个等腰直角三角形.
习题检测
2.解(1)如图,过B作AC的垂线,交AC于点O,则BO即为AC边上的高.
(2)延长CB,过A作CB延长线的垂线交延长线于F点.AF即为BC边上的高.
3.提示(1)(2)作△PQR的两边的垂直平分线,其交点即为体育中心G的位置.(3)旨在引发同学们对这一现实问题的进一步思考.实际上,对这类选址问题,从不同角度考虑会有不同的结论.
习题检测
4.解应选方案(3).
为方便起见,不妨设等边△ABC边长为a,
则对于方案(1)有AB+BC=2a;
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
