数学北师大版 八年级下册 2.6《一元一次不等式组》优秀教学课件 14张PPT
文档属性
| 名称 | 数学北师大版 八年级下册 2.6《一元一次不等式组》优秀教学课件 14张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 07:10:08 | ||
图片预览




文档简介
(共14张PPT)
第二章 第六节
一元一次不等式组
新课导入
思考:
1、在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形
2 、如何解不等式组3<2-3x<8
新课讲解
例1、解不等式组
解:解不等式①,得x>-1
②
①
解不等式② 得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
新课讲解
练习:
新课讲解
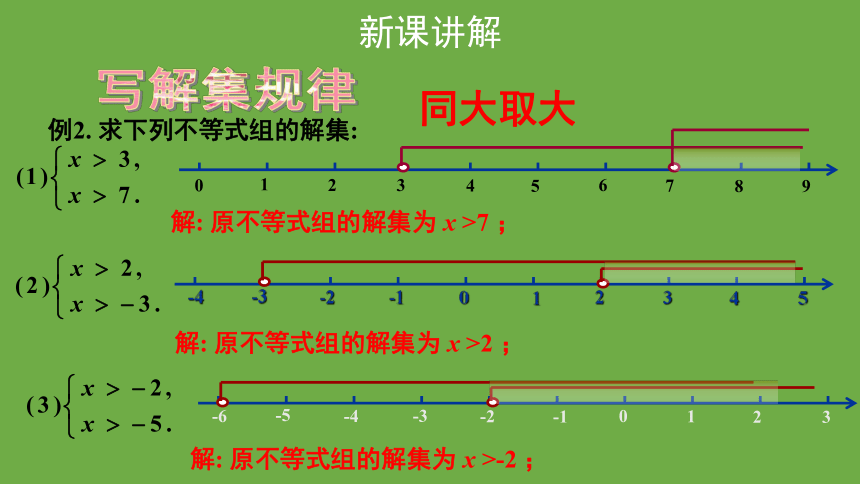
例2. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
同大取大
新课讲解
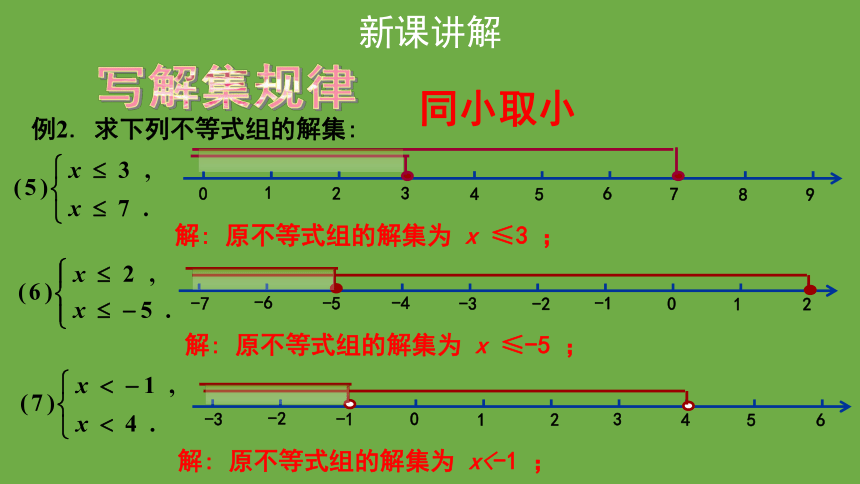
例2. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
写解集规律
同小取小
新课讲解
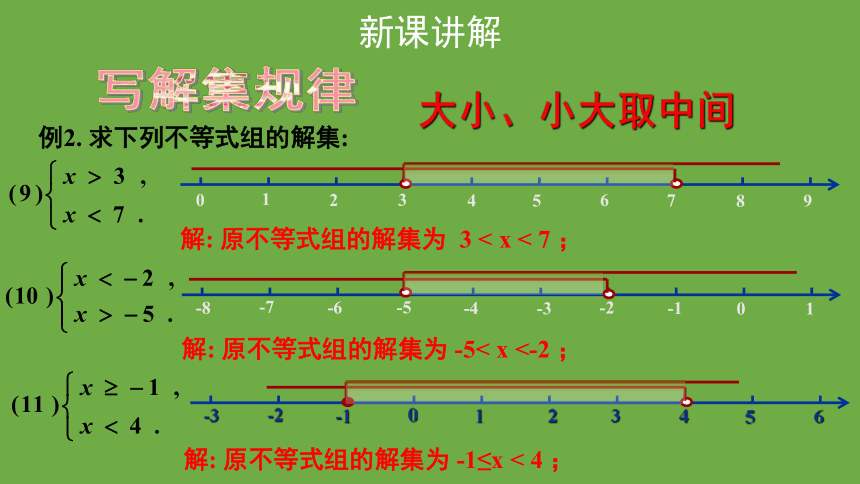
例2. 求下列不等式组的解集:
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
写解集规律
大小、小大取中间
新课讲解
例2. 求下列不等式组的解集:
解: 原不等式组无解 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组无解 ;
解: 原不等式组无解 ;
写解集规律
大大、小小解不了
新课讲解
同大取大
的解集是
当a>b时,
x>a
x>b
x>a
同小取小
的解集是
当a>b时,
x<a
x<b
x<b
大小小大取中间
的解集是
当a>b时,
x<a
x≥b
b ≤ x<a
大小等同取等值
x=a
的解集是
x≥a
x≤a
不等式组
大大小小则无解
的解集是
当a>b时,
x > a
x < b
无解
文字记忆
数学语言
图形
4.解集及记忆方法
a
b
a
b
a
b
a
a
b
新课讲解
例3 解不等式组
例4 当x取哪些整数时,不等式2(x+2)<x+5与3(x-2)+8>2x同时成立
例5 不等式组 的解集是x>a,则a的取值范围是 。
当堂检测
答案:-8解不等式
2、 解不等式 –5 < 2x +1 < 6
解: 原不等式就是不等式组
- 5 < 2x + 1
2x + 1 < 6
解这个不等式得:
- 3 < x < 2.5
所以,原不等式的解集为:- 3 < x < 2.5
同类练习:
1、是否存在实数x,使得 x + 3 < 5,且 x – 2 > 4
由x + 3 < 5 得 x < 2,
由 x – 2 > 4 得 x > 6
解:
所以,不存在实数x,使得 x + 3 < 5,且 x – 2 > 4
当堂检测
3、已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
解得: a=1 , b= - 2
4、当 x 取哪些整数时,不等式 2(x+2)<x+5 与3(x-2)+8>2x同时成立
答案: x= -1, x=0
课堂小结
1.由几个一元一次不等式组所组成的不等式组叫做一元一次不等式组
2.几个一元一次不等式的解集的公共部分, 叫做由它们所组成的一元一次不等式组的解集
3.求不等式组的解集的过程, 叫做 解不等式组
4.解简单一元一次不等式组的方法:
(1) 利用数轴找几个解集的公共部分:
(2) 利用规律: 同大取大;
同小取小;
大小、小大取中间;
大大、小小解不了(是空集)。
再见
第二章 第六节
一元一次不等式组
新课导入
思考:
1、在什么条件下,长度为3cm , 7cm , xcm的三条线段可以围成一个三角形
2 、如何解不等式组3<2-3x<8
新课讲解
例1、解不等式组
解:解不等式①,得x>-1
②
①
解不等式② 得
在数轴上表示它们的解集:
-3
-2
-1
0
4
2
1
3
5
解一元一次不等式组的步骤:
求出这个不等式组中各个不等式的解集
借助数轴求出这些不等式的解集的公共部分,即求出了这个不等式组的解集
新课讲解
练习:
新课讲解
例2. 求下列不等式组的解集:
解: 原不等式组的解集为 x >7 ;
解: 原不等式组的解集为 x >2 ;
写解集规律
0
7
6
5
4
2
1
3
8
9
-4
3
2
1
0
-2
-3
-1
4
5
解: 原不等式组的解集为 x >-2 ;
-6
1
0
-1
-2
-4
-5
-3
2
3
同大取大
新课讲解
例2. 求下列不等式组的解集:
解: 原不等式组的解集为 x ≤3 ;
解: 原不等式组的解集为 x ≤-5 ;
0
7
6
5
4
2
1
3
8
9
-7
0
-1
-2
-3
-5
-6
-4
1
2
解: 原不等式组的解集为 x<-1 ;
-3
4
3
2
1
-1
-2
0
5
6
写解集规律
同小取小
新课讲解
例2. 求下列不等式组的解集:
解: 原不等式组的解集为 3 < x < 7 ;
解: 原不等式组的解集为 -5< x <-2 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
解: 原不等式组的解集为 -1≤x < 4 ;
-3
4
3
2
1
-1
-2
0
5
6
写解集规律
大小、小大取中间
新课讲解
例2. 求下列不等式组的解集:
解: 原不等式组无解 ;
0
7
6
5
4
2
1
3
8
9
-8
-1
-2
-3
-4
-6
-7
-5
0
1
-3
4
3
2
1
-1
-2
0
5
6
解: 原不等式组无解 ;
解: 原不等式组无解 ;
写解集规律
大大、小小解不了
新课讲解
同大取大
的解集是
当a>b时,
x>a
x>b
x>a
同小取小
的解集是
当a>b时,
x<a
x<b
x<b
大小小大取中间
的解集是
当a>b时,
x<a
x≥b
b ≤ x<a
大小等同取等值
x=a
的解集是
x≥a
x≤a
不等式组
大大小小则无解
的解集是
当a>b时,
x > a
x < b
无解
文字记忆
数学语言
图形
4.解集及记忆方法
a
b
a
b
a
b
a
a
b
新课讲解
例3 解不等式组
例4 当x取哪些整数时,不等式2(x+2)<x+5与3(x-2)+8>2x同时成立
例5 不等式组 的解集是x>a,则a的取值范围是 。
当堂检测
答案:-8
2、 解不等式 –5 < 2x +1 < 6
解: 原不等式就是不等式组
- 5 < 2x + 1
2x + 1 < 6
解这个不等式得:
- 3 < x < 2.5
所以,原不等式的解集为:- 3 < x < 2.5
同类练习:
1、是否存在实数x,使得 x + 3 < 5,且 x – 2 > 4
由x + 3 < 5 得 x < 2,
由 x – 2 > 4 得 x > 6
解:
所以,不存在实数x,使得 x + 3 < 5,且 x – 2 > 4
当堂检测
3、已知不等式组 的解集为-1<x<1,
则(a+1)(b-1)的值为多少
2x—a<1
x—2b>3
解: 由不等式组得:
x <
x >3+2b
因为不等式组的解集为: -1< x < 1 ,
所以,
=1
3a+2b= -1
解得: a=1 , b= - 2
4、当 x 取哪些整数时,不等式 2(x+2)<x+5 与3(x-2)+8>2x同时成立
答案: x= -1, x=0
课堂小结
1.由几个一元一次不等式组所组成的不等式组叫做一元一次不等式组
2.几个一元一次不等式的解集的公共部分, 叫做由它们所组成的一元一次不等式组的解集
3.求不等式组的解集的过程, 叫做 解不等式组
4.解简单一元一次不等式组的方法:
(1) 利用数轴找几个解集的公共部分:
(2) 利用规律: 同大取大;
同小取小;
大小、小大取中间;
大大、小小解不了(是空集)。
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
