数学北师大版 八年级下册第一章 三角形的证明: 1.2《直角三角形》优秀教学课件 34张PPT
文档属性
| 名称 | 数学北师大版 八年级下册第一章 三角形的证明: 1.2《直角三角形》优秀教学课件 34张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 07:44:56 | ||
图片预览










文档简介
(共34张PPT)
第一章 第二节
直角三角形
知识要点
知识点一
知识点二
知识点三
知识点四
知识点一 直角三角形两锐角的关系
定理1:直角三角形的两个锐角互余.
定理2:有两个角互余的三角形是直角三角形.
拓展归纳 直角三角形的两锐角互余是三角形内角和等于180°的一个推论.当一个三角形有两个角互余(即两个角的和等于90°)时,第三个角是直角,此时,这个三角形是直角三角形.
例1 在△ABC中,∠A,∠B,∠C满足条件∠A∶∠B∶∠C=1∶2∶3.求证:△ABC是直角三角形.
分析:由三角形内角和等于180°,列方程求得最大角的度数.若最大角的度数等于90°,就可以确定这个三角形是直角三角形.
证明:∵∠A∶∠B∶∠C=1∶2∶3,且∠A+∠B+∠C=180°,∴∠A+∠B=∠C=90°.
∴△ABC是直角三角形.
知识要点
知识点一
知识点二
知识点三
知识点四
知识要点
知识点二 勾股定理及其逆定理
1.勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
2.勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
拓展归纳 勾股定理是以“一个三角形是直角三角形”为条件,进而得到这个直角三角形三边的数量关系“a2+b2=c2”;勾股定理的逆定理则是以“一个三角形的三边满足a2+b2=c2”为条件,进而得到这个三角形是直角三角形.
知识点一
知识点二
知识点三
知识点四
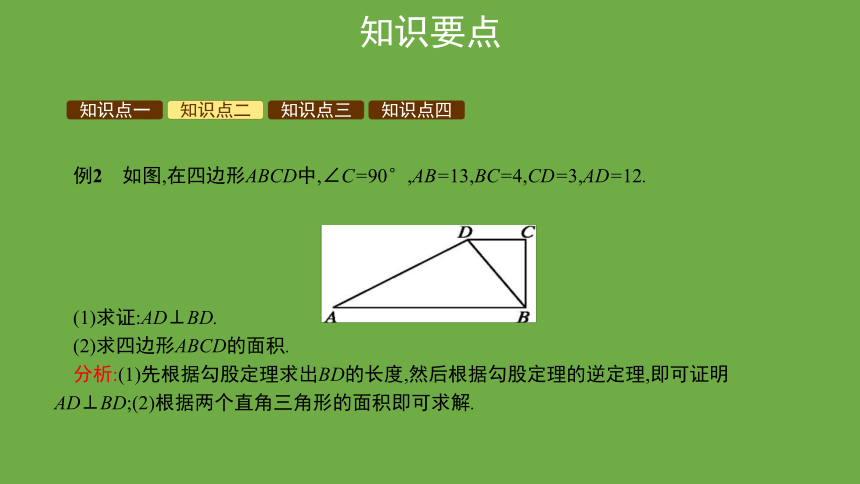
例2 如图,在四边形ABCD中,∠C=90°,AB=13,BC=4,CD=3,AD=12.
(1)求证:AD⊥BD.
(2)求四边形ABCD的面积.
分析:(1)先根据勾股定理求出BD的长度,然后根据勾股定理的逆定理,即可证明AD⊥BD;(2)根据两个直角三角形的面积即可求解.
知识要点
知识点一
知识点二
知识点三
知识点四
解:(1)在Rt△BCD中,由勾股定理得
在△ABD中,BD=5,AB=13,AD=12,
∵AD2+BD2=122+25=169=132=AB2,
即AD2+BD2=AB2,
∴由勾股定理的逆定理知△ABD是直角三角形,且∠ADB=90°.∴AD⊥BD.
(2)四边形ABCD的面积为
知识要点
知识点一
知识点二
知识点三
知识点四
知识要点
知识点一
知识点二
知识点三
知识点四
知识点三 互逆命题与互逆定理
1.互逆命题:在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
2.互逆定理:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
拓展归纳 (1)将一个命题的条件与结论互换,就得到这个命题的逆命题.相对于逆命题来说,原来的命题叫做原命题,原命题与逆命题是互逆的关系,因而是相对的,需要注意的是:原命题正确,逆命题不一定正确.
(2)命题都有逆命题,但定理不一定有逆定理.
知识要点
知识点一
知识点二
知识点三
知识点四
例3 (1)写出命题“如果a=b,那么a2=b2”的逆命题,并判断是不是真命题;
(2)写出定理“对顶角相等”的逆命题,并判断是不是原定理的逆定理.
分析:(1)该命题的条件与结论很清楚,只要将条件与结论互换即可得逆命题,逆命题的真假可通过举反例判断出.(2)此题的条件与结论都是略写的形式,要注意写出的命题必须是完整的,不能简单地说成“相等是对顶角”.
解:(1)逆命题是如果a2=b2,那么a=b,不是真命题.
(2)逆命题是如果两个角相等,那么这两个角是对顶角,这个命题是假命题,原以原定理没有逆定理.
知识要点
知识点一
知识点二
知识点三
知识点四
知识点四 直角三角形全等的判定
两个直角三角形全等除了应用一般三角形全等的判定方法外,还有特殊的判定定理.
定理:斜边和一条直角边分别相等的两个直角三角形全等.这一定理可以简述为“斜边、直角边”或“HL”.
拓展归纳 (1)“HL”是直角三角形所独有的判定三角形全等的定理,对于一般三角形不成立.判定两个直角三角形全等时,这两个直角三角形已经有一对直角相等的条件,只需找出另两个条件即可.而这两个条件中必须有一组边对应相等,与一般三角形全等的情形一样,只有三个角相等的两个直角三角形不一定全等(它们是相似的).
(2)直角三角形全等的判定,除了“HL”外,还可采用其他的判定方法,如“SAS”“ASA”“SSS”“AAS”等.
知识要点
知识点一
知识点二
知识点三
知识点四
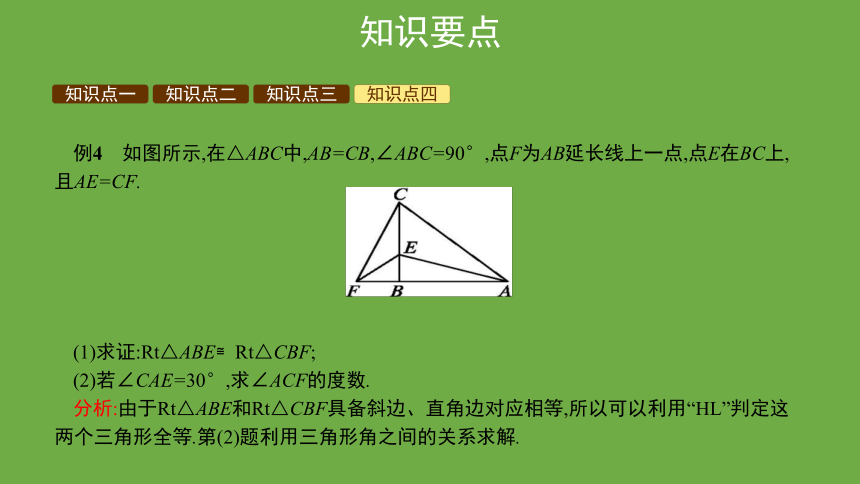
例4 如图所示,在△ABC中,AB=CB,∠ABC=90°,点F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
分析:由于Rt△ABE和Rt△CBF具备斜边、直角边对应相等,所以可以利用“HL”判定这两个三角形全等.第(2)题利用三角形角之间的关系求解.
知识要点
知识点一
知识点二
知识点三
知识点四
(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF,AB=BC,
∴Rt△ABE≌Rt△CBF(HL).
(2)解:∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
知识要点
知识点一
知识点二
知识点三
知识点四
知识要点
知识点一
知识点二
知识点三
知识点四
拓展延伸
拓展点一
拓展点二
拓展点一 利用勾股定理解决图形折叠问题
例1 如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8,折叠△ABC的一角,使点B与点A重合,展开得折痕DE,求BD的长.
分析:由折叠知△ADE≌△BDE得到AD=BD,在Rt△ACD中,由勾股定理求AD的长.
解:由折叠可知△ADE≌△BDE,AD=BD.
设BD=x,则AD=x,CD=8-x.
在Rt△ACD中,由勾股定理,得
AC2+CD2=AD2,即62+(8-x)2=x2,
拓展延伸
拓展点一
拓展点二
拓展延伸
拓展点二 添辅助线证直角三角形全等
例2 如图所示,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:CF=DF.
分析:通过添加辅助线,构造全等三角形,再通过证三角形全等得到线段相等.
拓展点一
拓展点二
拓展延伸
证明:如图,连接AC,AD,在△ABC和△AED中,
∵AB=AE,BC=ED,∠B=∠E,
∴△ABC≌△AED(SAS).
∴AC=AD.∵AF⊥DC,
∴∠AFC=∠AFD=90°.
在Rt△ACF和Rt△ADF中,
AC=AD,AF=AF,
∴Rt△AFC≌Rt△AFD(HL).
∴CF=DF.
拓展点一
拓展点二
拓展延伸
拓展点一
拓展点二
思考探究
P15 议一议
第一个定理的条件和结论分别是第二个定理的结论和条件.第三个定理的条件和结论分别是第四个定理的结论和条件.所列的三组命题每组中两个命题的条件和结论也有类似的关系.
P16 想一想
答案逆命题为:“如果两个有理数的平方相等,那么这两个有理数也相等”.
原命题是真命题,它的逆命题是假命题.
P16 随堂练习
1.解 在△ABC中,∠C=180°-∠A-∠B=180°-45°-45°=90°,
∴△ABC是等腰直角三角形.
∴AC=CB=3.
思考探究
2.证法1如图,
∵AD是BC边上的中线,
在△ABD中,∵AB=13 cm,AD=12 cm,BD=5 cm,
∴AB2=AD2+BD2.
∴△ABD为直角三角形.∴AD⊥BC.
∴AB=AC=13 cm.
思考探究
证法2∵AD是BC边上的中线,
在△ABD中,∵AB=13 cm,AD=12 cm,BD=5 cm,
∴AB2=AD2+BD2.
∴△ABD为直角三角形.
∴AD⊥BC.
∴∠ADB=∠ADC=90°.
∴△ADB≌△ADC(SAS).
∴AB=AC.
思考探究
3.解(1)多边形是四边形,假命题,而原命题是真命题.
(2)同旁内角互补,两直线平行,这对命题都是真命题.
(3)如果a=0,b=0,那么ab=0,原命题是假命题,其逆命题为真命题.
习题检测
习题1.5
1.解∵AB∥DC,
∴∠BAD+∠ADC=180°.
∴∠BAE+∠EAD+∠ADE+∠EDC=180°.
∴25°+∠EAD+∠ADE+65°=180°.
∴∠EAD+∠ADE=180°-25°-65°=90°.
∴∠AED=180°-(∠EAD+∠ADE)=180°-90°=90°.
∴AE⊥DE.
∴△AED是直角三角形.
2.解如图,在Rt△ABC中,
∵∠A=30°,
习题检测
习题检测
3.解由题意,△DEB为直角三角形.
∵∠BDE=30°,∴BD=2BE.
用勾股定理有BE2+ED2=BD2=(2BE)2,
∴BE2+302=4BE2,
解得BE=10 ≈17.32(m).
∴树高为BE+AD=17.32+1.52≈18.8(m).
答:大树高约18.8 m.
4.解没有.
∵452+602=5 625≠4 900=702,
∴这个三角形无直角.
∴当长60 m的线段为南北向时,无东西向的边.
习题检测
5.解如图(1),将棱柱展开,则此时A与C‘在一个平面内,
习题检测
P18问题
答案在上一节我们已经学过,两边分别相等且其中一组等边的对角分别相等的两个三角形不一定全等.
如果其中一组等边所对的角是直角,那么可以判定它们全等.
随堂练习
P20随堂练习
1.解(1)假命题.如图(1),在△ABC与△A'B'C'中,∠A=∠A'=90°,∠B=∠C=45°=∠B'=∠C',AB≠A'B',BC≠B'C',则Rt△ABC与Rt△A'B'C'不全等.
(2)真命题.满足AAS公理.
(3)真命题.满足SAS公理.
随堂练习
(4)真命题.
已知:如图(2),在Rt△ABC与Rt△A'B'C'中,AC=A'C',AD,A'D'分别是BC,B'C'边上的中线,且AD=A'D'.
求证:Rt△ABC≌Rt△A'B'C'.
证明:在Rt△ACD与Rt△A'C'D'中,
∵AC=A'C',AD=A'D',
∴Rt△ACD≌Rt△A'C'D'(HL).
∴CD=C'D'.
∵AD,A'D'分别是BC,B'C'边上的中线,
∴BC=B'C'.
又∵AC=A'C',∠C=∠C'=90°,
∴Rt△ABC≌△Rt△A'B'C'(SAS).
随堂练习
2.答:相等.
理由如下:∵AB=AC=12,
∴△ABC是等腰三角形.
又∵AO⊥BC,
∴BO=OC(三线合一),
∴两木桩离旗杆底部的距离相等.
随堂练习
习题1.6
1.证明∵D为BC的中点,∴BD=DC.
又∵DE=DF,
∴Rt△BDF≌Rt△CDE(HL).
∴∠B=∠C.∴AB=AC,
即△ABC为等腰三角形.
2.证明(1)∵AB=CD,BF=DE,
∴Rt△ABF≌Rt△CDE(HL).
∴AF=CE.
∴AF-EF=CE-EF,即AE=CF.
(2)∵Rt△ABF≌Rt△CDE,∴∠A=∠C.
∴AB∥CD.
随堂练习
3.证明∵MP⊥OM,NP⊥ON,
∴∠OMP=∠ONP=90°.
∴Rt△OMP≌Rt△ONP(HL).
∴∠MOP=∠NOP(全等三角形的对应边相等),
∴射线OP是∠AOB的平分线.
4.解(1)真命题.
情况一:两条直角边相等,加上直角,能满足SAS,故全等.
情况二:若是一条直角边和一条斜边相等,则满足HL定理,也能全等.
(2)真命题.
满足ASA或AAS定理.
随堂练习
5.(1)解AC=AE=BE,AD=BD,CD=DE= AD,
∠CAD=∠BAD=∠B=30°,∠ADC=∠ADE=∠BDE=60°,∠AED=∠BED=90°.
(2)证明由折叠知:∠AED=∠C=90°,CD=ED.
又∵AD=AD,∴△ACD≌△AED(HL).
(3)不能.
再见
第一章 第二节
直角三角形
知识要点
知识点一
知识点二
知识点三
知识点四
知识点一 直角三角形两锐角的关系
定理1:直角三角形的两个锐角互余.
定理2:有两个角互余的三角形是直角三角形.
拓展归纳 直角三角形的两锐角互余是三角形内角和等于180°的一个推论.当一个三角形有两个角互余(即两个角的和等于90°)时,第三个角是直角,此时,这个三角形是直角三角形.
例1 在△ABC中,∠A,∠B,∠C满足条件∠A∶∠B∶∠C=1∶2∶3.求证:△ABC是直角三角形.
分析:由三角形内角和等于180°,列方程求得最大角的度数.若最大角的度数等于90°,就可以确定这个三角形是直角三角形.
证明:∵∠A∶∠B∶∠C=1∶2∶3,且∠A+∠B+∠C=180°,∴∠A+∠B=∠C=90°.
∴△ABC是直角三角形.
知识要点
知识点一
知识点二
知识点三
知识点四
知识要点
知识点二 勾股定理及其逆定理
1.勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
2.勾股定理的逆定理:如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
拓展归纳 勾股定理是以“一个三角形是直角三角形”为条件,进而得到这个直角三角形三边的数量关系“a2+b2=c2”;勾股定理的逆定理则是以“一个三角形的三边满足a2+b2=c2”为条件,进而得到这个三角形是直角三角形.
知识点一
知识点二
知识点三
知识点四
例2 如图,在四边形ABCD中,∠C=90°,AB=13,BC=4,CD=3,AD=12.
(1)求证:AD⊥BD.
(2)求四边形ABCD的面积.
分析:(1)先根据勾股定理求出BD的长度,然后根据勾股定理的逆定理,即可证明AD⊥BD;(2)根据两个直角三角形的面积即可求解.
知识要点
知识点一
知识点二
知识点三
知识点四
解:(1)在Rt△BCD中,由勾股定理得
在△ABD中,BD=5,AB=13,AD=12,
∵AD2+BD2=122+25=169=132=AB2,
即AD2+BD2=AB2,
∴由勾股定理的逆定理知△ABD是直角三角形,且∠ADB=90°.∴AD⊥BD.
(2)四边形ABCD的面积为
知识要点
知识点一
知识点二
知识点三
知识点四
知识要点
知识点一
知识点二
知识点三
知识点四
知识点三 互逆命题与互逆定理
1.互逆命题:在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.
2.互逆定理:如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
拓展归纳 (1)将一个命题的条件与结论互换,就得到这个命题的逆命题.相对于逆命题来说,原来的命题叫做原命题,原命题与逆命题是互逆的关系,因而是相对的,需要注意的是:原命题正确,逆命题不一定正确.
(2)命题都有逆命题,但定理不一定有逆定理.
知识要点
知识点一
知识点二
知识点三
知识点四
例3 (1)写出命题“如果a=b,那么a2=b2”的逆命题,并判断是不是真命题;
(2)写出定理“对顶角相等”的逆命题,并判断是不是原定理的逆定理.
分析:(1)该命题的条件与结论很清楚,只要将条件与结论互换即可得逆命题,逆命题的真假可通过举反例判断出.(2)此题的条件与结论都是略写的形式,要注意写出的命题必须是完整的,不能简单地说成“相等是对顶角”.
解:(1)逆命题是如果a2=b2,那么a=b,不是真命题.
(2)逆命题是如果两个角相等,那么这两个角是对顶角,这个命题是假命题,原以原定理没有逆定理.
知识要点
知识点一
知识点二
知识点三
知识点四
知识点四 直角三角形全等的判定
两个直角三角形全等除了应用一般三角形全等的判定方法外,还有特殊的判定定理.
定理:斜边和一条直角边分别相等的两个直角三角形全等.这一定理可以简述为“斜边、直角边”或“HL”.
拓展归纳 (1)“HL”是直角三角形所独有的判定三角形全等的定理,对于一般三角形不成立.判定两个直角三角形全等时,这两个直角三角形已经有一对直角相等的条件,只需找出另两个条件即可.而这两个条件中必须有一组边对应相等,与一般三角形全等的情形一样,只有三个角相等的两个直角三角形不一定全等(它们是相似的).
(2)直角三角形全等的判定,除了“HL”外,还可采用其他的判定方法,如“SAS”“ASA”“SSS”“AAS”等.
知识要点
知识点一
知识点二
知识点三
知识点四
例4 如图所示,在△ABC中,AB=CB,∠ABC=90°,点F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
分析:由于Rt△ABE和Rt△CBF具备斜边、直角边对应相等,所以可以利用“HL”判定这两个三角形全等.第(2)题利用三角形角之间的关系求解.
知识要点
知识点一
知识点二
知识点三
知识点四
(1)证明:∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE和Rt△CBF中,
∵AE=CF,AB=BC,
∴Rt△ABE≌Rt△CBF(HL).
(2)解:∵AB=BC,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∵∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.
知识要点
知识点一
知识点二
知识点三
知识点四
知识要点
知识点一
知识点二
知识点三
知识点四
拓展延伸
拓展点一
拓展点二
拓展点一 利用勾股定理解决图形折叠问题
例1 如图,直角三角形纸片ABC,∠C=90°,AC=6,BC=8,折叠△ABC的一角,使点B与点A重合,展开得折痕DE,求BD的长.
分析:由折叠知△ADE≌△BDE得到AD=BD,在Rt△ACD中,由勾股定理求AD的长.
解:由折叠可知△ADE≌△BDE,AD=BD.
设BD=x,则AD=x,CD=8-x.
在Rt△ACD中,由勾股定理,得
AC2+CD2=AD2,即62+(8-x)2=x2,
拓展延伸
拓展点一
拓展点二
拓展延伸
拓展点二 添辅助线证直角三角形全等
例2 如图所示,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD,F为垂足,求证:CF=DF.
分析:通过添加辅助线,构造全等三角形,再通过证三角形全等得到线段相等.
拓展点一
拓展点二
拓展延伸
证明:如图,连接AC,AD,在△ABC和△AED中,
∵AB=AE,BC=ED,∠B=∠E,
∴△ABC≌△AED(SAS).
∴AC=AD.∵AF⊥DC,
∴∠AFC=∠AFD=90°.
在Rt△ACF和Rt△ADF中,
AC=AD,AF=AF,
∴Rt△AFC≌Rt△AFD(HL).
∴CF=DF.
拓展点一
拓展点二
拓展延伸
拓展点一
拓展点二
思考探究
P15 议一议
第一个定理的条件和结论分别是第二个定理的结论和条件.第三个定理的条件和结论分别是第四个定理的结论和条件.所列的三组命题每组中两个命题的条件和结论也有类似的关系.
P16 想一想
答案逆命题为:“如果两个有理数的平方相等,那么这两个有理数也相等”.
原命题是真命题,它的逆命题是假命题.
P16 随堂练习
1.解 在△ABC中,∠C=180°-∠A-∠B=180°-45°-45°=90°,
∴△ABC是等腰直角三角形.
∴AC=CB=3.
思考探究
2.证法1如图,
∵AD是BC边上的中线,
在△ABD中,∵AB=13 cm,AD=12 cm,BD=5 cm,
∴AB2=AD2+BD2.
∴△ABD为直角三角形.∴AD⊥BC.
∴AB=AC=13 cm.
思考探究
证法2∵AD是BC边上的中线,
在△ABD中,∵AB=13 cm,AD=12 cm,BD=5 cm,
∴AB2=AD2+BD2.
∴△ABD为直角三角形.
∴AD⊥BC.
∴∠ADB=∠ADC=90°.
∴△ADB≌△ADC(SAS).
∴AB=AC.
思考探究
3.解(1)多边形是四边形,假命题,而原命题是真命题.
(2)同旁内角互补,两直线平行,这对命题都是真命题.
(3)如果a=0,b=0,那么ab=0,原命题是假命题,其逆命题为真命题.
习题检测
习题1.5
1.解∵AB∥DC,
∴∠BAD+∠ADC=180°.
∴∠BAE+∠EAD+∠ADE+∠EDC=180°.
∴25°+∠EAD+∠ADE+65°=180°.
∴∠EAD+∠ADE=180°-25°-65°=90°.
∴∠AED=180°-(∠EAD+∠ADE)=180°-90°=90°.
∴AE⊥DE.
∴△AED是直角三角形.
2.解如图,在Rt△ABC中,
∵∠A=30°,
习题检测
习题检测
3.解由题意,△DEB为直角三角形.
∵∠BDE=30°,∴BD=2BE.
用勾股定理有BE2+ED2=BD2=(2BE)2,
∴BE2+302=4BE2,
解得BE=10 ≈17.32(m).
∴树高为BE+AD=17.32+1.52≈18.8(m).
答:大树高约18.8 m.
4.解没有.
∵452+602=5 625≠4 900=702,
∴这个三角形无直角.
∴当长60 m的线段为南北向时,无东西向的边.
习题检测
5.解如图(1),将棱柱展开,则此时A与C‘在一个平面内,
习题检测
P18问题
答案在上一节我们已经学过,两边分别相等且其中一组等边的对角分别相等的两个三角形不一定全等.
如果其中一组等边所对的角是直角,那么可以判定它们全等.
随堂练习
P20随堂练习
1.解(1)假命题.如图(1),在△ABC与△A'B'C'中,∠A=∠A'=90°,∠B=∠C=45°=∠B'=∠C',AB≠A'B',BC≠B'C',则Rt△ABC与Rt△A'B'C'不全等.
(2)真命题.满足AAS公理.
(3)真命题.满足SAS公理.
随堂练习
(4)真命题.
已知:如图(2),在Rt△ABC与Rt△A'B'C'中,AC=A'C',AD,A'D'分别是BC,B'C'边上的中线,且AD=A'D'.
求证:Rt△ABC≌Rt△A'B'C'.
证明:在Rt△ACD与Rt△A'C'D'中,
∵AC=A'C',AD=A'D',
∴Rt△ACD≌Rt△A'C'D'(HL).
∴CD=C'D'.
∵AD,A'D'分别是BC,B'C'边上的中线,
∴BC=B'C'.
又∵AC=A'C',∠C=∠C'=90°,
∴Rt△ABC≌△Rt△A'B'C'(SAS).
随堂练习
2.答:相等.
理由如下:∵AB=AC=12,
∴△ABC是等腰三角形.
又∵AO⊥BC,
∴BO=OC(三线合一),
∴两木桩离旗杆底部的距离相等.
随堂练习
习题1.6
1.证明∵D为BC的中点,∴BD=DC.
又∵DE=DF,
∴Rt△BDF≌Rt△CDE(HL).
∴∠B=∠C.∴AB=AC,
即△ABC为等腰三角形.
2.证明(1)∵AB=CD,BF=DE,
∴Rt△ABF≌Rt△CDE(HL).
∴AF=CE.
∴AF-EF=CE-EF,即AE=CF.
(2)∵Rt△ABF≌Rt△CDE,∴∠A=∠C.
∴AB∥CD.
随堂练习
3.证明∵MP⊥OM,NP⊥ON,
∴∠OMP=∠ONP=90°.
∴Rt△OMP≌Rt△ONP(HL).
∴∠MOP=∠NOP(全等三角形的对应边相等),
∴射线OP是∠AOB的平分线.
4.解(1)真命题.
情况一:两条直角边相等,加上直角,能满足SAS,故全等.
情况二:若是一条直角边和一条斜边相等,则满足HL定理,也能全等.
(2)真命题.
满足ASA或AAS定理.
随堂练习
5.(1)解AC=AE=BE,AD=BD,CD=DE= AD,
∠CAD=∠BAD=∠B=30°,∠ADC=∠ADE=∠BDE=60°,∠AED=∠BED=90°.
(2)证明由折叠知:∠AED=∠C=90°,CD=ED.
又∵AD=AD,∴△ACD≌△AED(HL).
(3)不能.
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
