1.4.1用空间向量研究直线、平面的位置关系(第1课时)课件(共27张PPT)
文档属性
| 名称 | 1.4.1用空间向量研究直线、平面的位置关系(第1课时)课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 840.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 17:41:58 | ||
图片预览




文档简介
(共27张PPT)
1.4.1
用空间向量研究直线、平面的位置关系
(第1课时)
人教A版(2019)选择性必修第一册
学习目标
1.能用向量表达空中的点、线和平面.
2.会求直线的方向向量和平面的法向量.
3.能用向量表达直线与直线、直线与平面、平面与平面的平行关系.
4.能用向量方法判断或证明直线、平面间的平行关系.
5.核心素养:数学抽象、直观想象、数学运算
一、问题导入
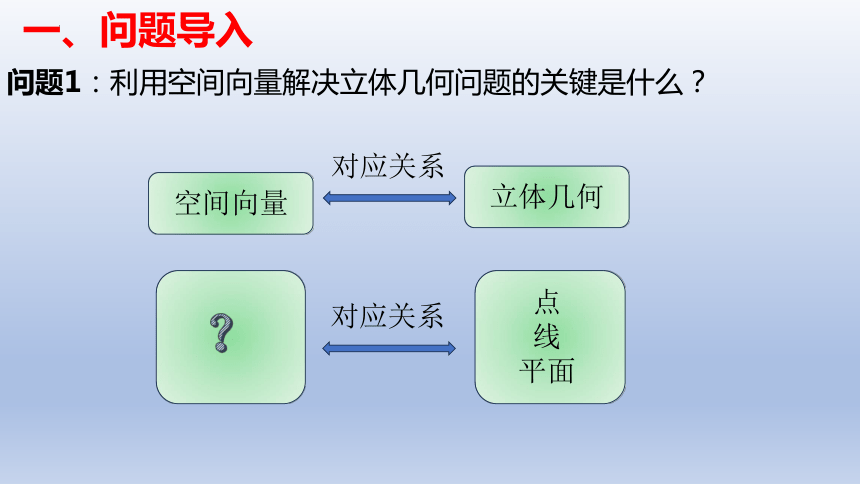
问题1:利用空间向量解决立体几何问题的关键是什么?
空间向量
立体几何
对应关系
对应关系
点
线
平面
?
二、新课讲授
1、空间中点、直线和平面的向量表示
问题1:如何用向量表示空间中的一个点P?
P
O
向量称为点P的位置向量
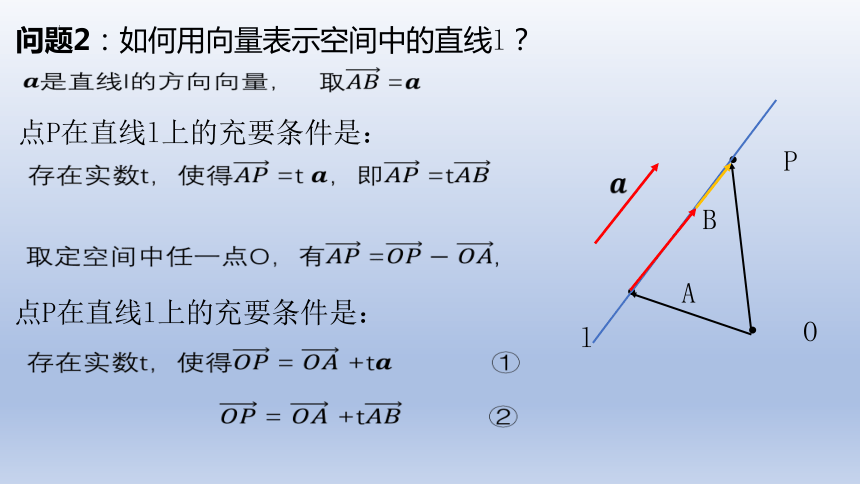
问题2:如何用向量表示空间中的直线l?
P
A
取=
B
l
是直线l的方向向量,
点P在直线l上的充要条件是:
存在实数t,使得=t 即=t
O
取定空间中任一点O,有= ,
点P在直线l上的充要条件是:
存在实数t,使得= +t ①
= +t ②
= +t
点A和方向向量不仅能确定直线l的位置,还可以表示出直线l上的任意一点
= +t ①
= +t ②
①式和②式都称为空间直线的向量表示式
空间任意直线由直线上一点A及直线的方向向量唯一确定
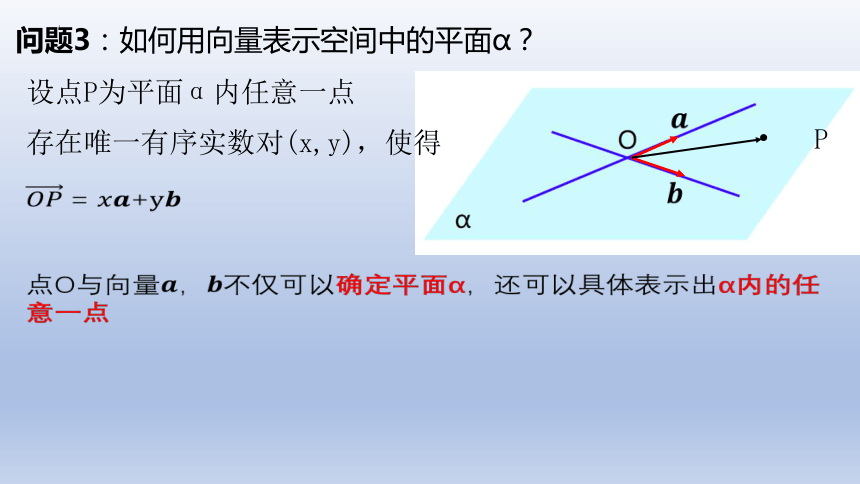
问题3:如何用向量表示空间中的平面α?
P
设点P为平面α内任意一点
存在唯一有序实数对(x,y),使得
= +
点O与向量不仅可以确定平面α,还可以具体表示出α内的任意一点
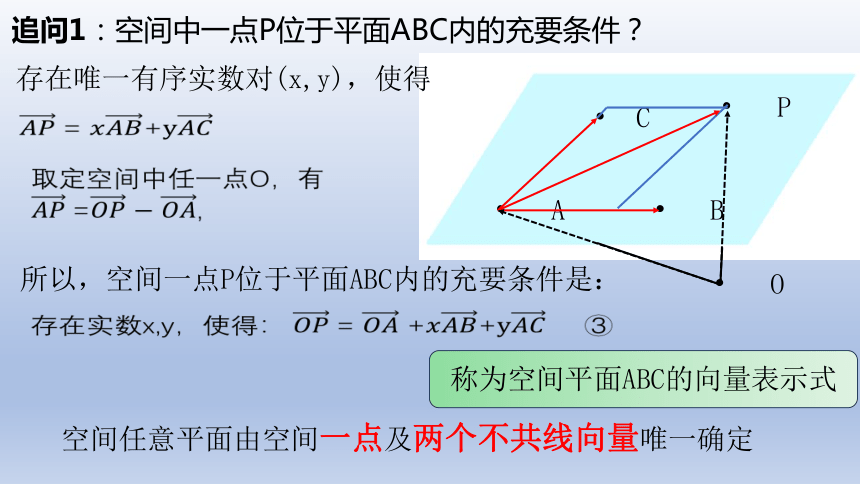
追问1:空间中一点P位于平面ABC内的充要条件?
A
B
C
P
存在唯一有序实数对(x,y),使得
= +
取定空间中任一点O,有
= ,
O
所以,空间一点P位于平面ABC内的充要条件是:
存在实数x,y,使得: = ++ ③
称为空间平面ABC的向量表示式
空间任意平面由空间一点及两个不共线向量唯一确定
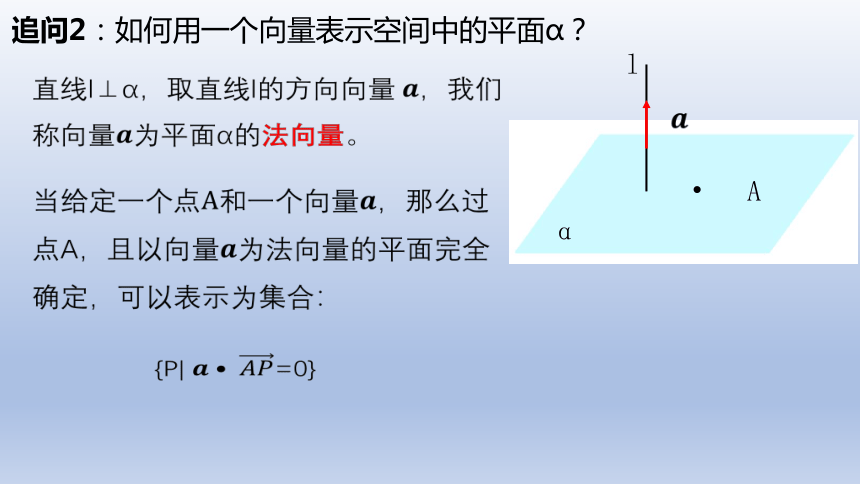
追问2:如何用一个向量表示空间中的平面α?
A
l
α
直线l⊥α,取直线l的方向向量 ,我们
称向量为平面α的法向量。
当,那么过点A,且以向量为法向量的平面完全确定,可以表示为集合:
{P| =0}
追问3:如果另有一条直线m⊥α,在直线m上任取向量, 与什么关系?
l
α
因为l⊥α, m⊥α ,
m
所以l∥ m
所以∥
所以R,使得=
所以{P| =0}={P|=0}={P|=0}
所以,平面α可以由平面内一点和任意法向量唯一确定
例1 如图所示,在长方体ABCD-A B C D 中,AB=4,BC=3,C C =2,M·是AB的中点.以D为原点,DA,DC,D D 所在直线分别为x轴、y轴,z轴,建立如图所示的空间直角坐标系.
(1)求直线CD的方向向量
(2)求平面BC C B 的法向量
(3)求平面MC A 的法向量
2、直线方向向量和平面法向量的求解
解:(1)根据题意可知
D(0,0,0),C(0,4,0)
所以直线CD的方向向量是
=(0,4,0)
追问1:直线CD还有其他的方向向量吗?
=(0,-4,0)
(0,1,0)
(0,a,0)(a≠0)
共线向量
(2)求平面BC C B 的法向量
解:(2)因为在长方体ABCD-A B C D 中,
所以DC⊥平面BC C B
所以平面BC C B 的一个法向量是
=(0,4,0)
追问2:平面BC C B 还有其他的法向量吗?
因为D C ⊥平面BC C B ,所以也是平面的法向量
=(0,4,0)
=(0,4,0)
=(0,4,0)
(0,1,0)
(0,a,0)(a≠0)
共线向量
(3)求平面MC A 的法向量
解:(3) AB=4,BC=3,C C =2,M·是AB的中点
所以M(3,2,0),C(0,4,0),A(3,0,2)
所以=(-3,2,0), =(0,-2,2)
设=(x,y,z)是平面MC A 的法向量,则
⊥ , ⊥
所以
所以
取z=3,则x=2,y=3
所以=(2,3,3)是平面MC A 的法向量
小结:(1)同一条直线的方向向量有无穷多个,它们互相平行.
(2)同一个平面的法向量有无穷多个,它们互相平行.
(3)直线方向向量和平面法向量的求法:
向量的名称 图示 求法
①找到l⊥α;
②l的方向向量即为平面的法向量
①取两点;②定向量
①设面α的法向量;②求面α内的不共线向量;③列方程组;④解方程组,得出结论
平面的法向量
直线的方向向量
A
B
n
小结:求平面法向量的步骤
(1)设平面=(x,y,z).
(2)找出=(x,y,z), =(x,y,z).
(3)根据法向量的定义建立关于x,y,z 方程组
所以
(4)解方程组,取其中一组解,即得平面法向量.
3、空间中直线、平面的平行
问题4:由直线与直线的平行关系,可以得到这两条直线的方向向量有什么关系呢?
设, 分别是直线, 的方向向量,
∥ ∥
λ∈R,
问题5:由直线与平面的平行关系,可以得到直线的方向向量与平面的法向量有什么关系呢?
设是直线的方向向量,
是平面α的法向量,
⊥
=0
问题5:由平面与平面的平行关系,可以得到着两个平面的法向量有什么关系呢?
设, 分别是平面α,β的法向量,
∥ β ∥
λ∈R,使得
三、巩固新知
例2 “平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,a β, b β,a∩b=P,a∥ , b∥ .
求证: ∥β
n
u
v
Q
证明:设平面,直线a,b的方向向量分别为
因为a∥ , b∥ ,所以⊥, ⊥
即 =0, =0
又因为a β, b β,a∩b=P,
所以对任意点Q∈β, x,y∈R,
使得= +
从而= +=0,即
所以平面β的法向量,故 ∥β
向量运算
例3 如图,在长方体ABCD-A B C D 中,AB=4,BC=3,C C =2.在线段B C上是否存在点P,使得A P∥平面AC D ?
解:以D为原点,DA,DC,D D 所在直线分别为x轴,y轴,z轴,
建立如图所示的空间直角坐标系Dxyz。
可得,A(3,0,0),C(0,4,0), D (0,0,2)。
所以 = (-3,4,0) , = (-3,0,2) 。
设=(x,y,z)是平面AC D 的法向量,则
= 0, = 0,即
所以
所以
取z=6,则x=4,y=3
于是=(4,3,6)是平面AC D 的法向量
又有于, A (3,0,2),C(0,4,0), B (3,4,2)。
所以 = (0,4,0) , = (-3,0,-2) 。
设点P满足=λ (0≤ λ ≤1),则
= (-3λ,0,-2λ) (0≤ λ ≤1),
所以 = += (-3λ,4,-2λ)
令 =0,得-12λ+12-12λ=0
解得λ=
所以这样的点P存在
当= ,即P为B C中点时, A P∥平面AC D
小结:用向量法解决立体几何问题的步骤
(1)建系.
(2)设点.
(3)表示相关向量
(4)进行向量运算.
(5)把向量运算的结果“翻译”为几何结论.
线面的位置关系 向量的位置关系 向量的运算 向量运算的坐标表示
∥
∥ β
∥
⊥
λ∈R,使得
= =
=0
其中,=(x,y,z), = (, , ), , 是直线l的方向向量; = (, ,), = (, ,), 分别是平面α,β的法向量
+ =0
∥
λ∈R,使得
= =
四、课堂小结
1.能用向量表达空中的点、线和平面.
2. 直线的方向向量和平面的法向量的求解.
3.线线、线面、面面平行关系向量表达.
4. 直线、平面间平行关系的向量法证明.
五、作业布置
课本P29:练习 第2、3题
将几何对象(点、线、面)向量化
用向量方法解决立体几何问题的基础
1.4.1
用空间向量研究直线、平面的位置关系
(第1课时)
人教A版(2019)选择性必修第一册
学习目标
1.能用向量表达空中的点、线和平面.
2.会求直线的方向向量和平面的法向量.
3.能用向量表达直线与直线、直线与平面、平面与平面的平行关系.
4.能用向量方法判断或证明直线、平面间的平行关系.
5.核心素养:数学抽象、直观想象、数学运算
一、问题导入
问题1:利用空间向量解决立体几何问题的关键是什么?
空间向量
立体几何
对应关系
对应关系
点
线
平面
?
二、新课讲授
1、空间中点、直线和平面的向量表示
问题1:如何用向量表示空间中的一个点P?
P
O
向量称为点P的位置向量
问题2:如何用向量表示空间中的直线l?
P
A
取=
B
l
是直线l的方向向量,
点P在直线l上的充要条件是:
存在实数t,使得=t 即=t
O
取定空间中任一点O,有= ,
点P在直线l上的充要条件是:
存在实数t,使得= +t ①
= +t ②
= +t
点A和方向向量不仅能确定直线l的位置,还可以表示出直线l上的任意一点
= +t ①
= +t ②
①式和②式都称为空间直线的向量表示式
空间任意直线由直线上一点A及直线的方向向量唯一确定
问题3:如何用向量表示空间中的平面α?
P
设点P为平面α内任意一点
存在唯一有序实数对(x,y),使得
= +
点O与向量不仅可以确定平面α,还可以具体表示出α内的任意一点
追问1:空间中一点P位于平面ABC内的充要条件?
A
B
C
P
存在唯一有序实数对(x,y),使得
= +
取定空间中任一点O,有
= ,
O
所以,空间一点P位于平面ABC内的充要条件是:
存在实数x,y,使得: = ++ ③
称为空间平面ABC的向量表示式
空间任意平面由空间一点及两个不共线向量唯一确定
追问2:如何用一个向量表示空间中的平面α?
A
l
α
直线l⊥α,取直线l的方向向量 ,我们
称向量为平面α的法向量。
当,那么过点A,且以向量为法向量的平面完全确定,可以表示为集合:
{P| =0}
追问3:如果另有一条直线m⊥α,在直线m上任取向量, 与什么关系?
l
α
因为l⊥α, m⊥α ,
m
所以l∥ m
所以∥
所以R,使得=
所以{P| =0}={P|=0}={P|=0}
所以,平面α可以由平面内一点和任意法向量唯一确定
例1 如图所示,在长方体ABCD-A B C D 中,AB=4,BC=3,C C =2,M·是AB的中点.以D为原点,DA,DC,D D 所在直线分别为x轴、y轴,z轴,建立如图所示的空间直角坐标系.
(1)求直线CD的方向向量
(2)求平面BC C B 的法向量
(3)求平面MC A 的法向量
2、直线方向向量和平面法向量的求解
解:(1)根据题意可知
D(0,0,0),C(0,4,0)
所以直线CD的方向向量是
=(0,4,0)
追问1:直线CD还有其他的方向向量吗?
=(0,-4,0)
(0,1,0)
(0,a,0)(a≠0)
共线向量
(2)求平面BC C B 的法向量
解:(2)因为在长方体ABCD-A B C D 中,
所以DC⊥平面BC C B
所以平面BC C B 的一个法向量是
=(0,4,0)
追问2:平面BC C B 还有其他的法向量吗?
因为D C ⊥平面BC C B ,所以也是平面的法向量
=(0,4,0)
=(0,4,0)
=(0,4,0)
(0,1,0)
(0,a,0)(a≠0)
共线向量
(3)求平面MC A 的法向量
解:(3) AB=4,BC=3,C C =2,M·是AB的中点
所以M(3,2,0),C(0,4,0),A(3,0,2)
所以=(-3,2,0), =(0,-2,2)
设=(x,y,z)是平面MC A 的法向量,则
⊥ , ⊥
所以
所以
取z=3,则x=2,y=3
所以=(2,3,3)是平面MC A 的法向量
小结:(1)同一条直线的方向向量有无穷多个,它们互相平行.
(2)同一个平面的法向量有无穷多个,它们互相平行.
(3)直线方向向量和平面法向量的求法:
向量的名称 图示 求法
①找到l⊥α;
②l的方向向量即为平面的法向量
①取两点;②定向量
①设面α的法向量;②求面α内的不共线向量;③列方程组;④解方程组,得出结论
平面的法向量
直线的方向向量
A
B
n
小结:求平面法向量的步骤
(1)设平面=(x,y,z).
(2)找出=(x,y,z), =(x,y,z).
(3)根据法向量的定义建立关于x,y,z 方程组
所以
(4)解方程组,取其中一组解,即得平面法向量.
3、空间中直线、平面的平行
问题4:由直线与直线的平行关系,可以得到这两条直线的方向向量有什么关系呢?
设, 分别是直线, 的方向向量,
∥ ∥
λ∈R,
问题5:由直线与平面的平行关系,可以得到直线的方向向量与平面的法向量有什么关系呢?
设是直线的方向向量,
是平面α的法向量,
⊥
=0
问题5:由平面与平面的平行关系,可以得到着两个平面的法向量有什么关系呢?
设, 分别是平面α,β的法向量,
∥ β ∥
λ∈R,使得
三、巩固新知
例2 “平面与平面平行的判定定理”:若一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
已知:如图,a β, b β,a∩b=P,a∥ , b∥ .
求证: ∥β
n
u
v
Q
证明:设平面,直线a,b的方向向量分别为
因为a∥ , b∥ ,所以⊥, ⊥
即 =0, =0
又因为a β, b β,a∩b=P,
所以对任意点Q∈β, x,y∈R,
使得= +
从而= +=0,即
所以平面β的法向量,故 ∥β
向量运算
例3 如图,在长方体ABCD-A B C D 中,AB=4,BC=3,C C =2.在线段B C上是否存在点P,使得A P∥平面AC D ?
解:以D为原点,DA,DC,D D 所在直线分别为x轴,y轴,z轴,
建立如图所示的空间直角坐标系Dxyz。
可得,A(3,0,0),C(0,4,0), D (0,0,2)。
所以 = (-3,4,0) , = (-3,0,2) 。
设=(x,y,z)是平面AC D 的法向量,则
= 0, = 0,即
所以
所以
取z=6,则x=4,y=3
于是=(4,3,6)是平面AC D 的法向量
又有于, A (3,0,2),C(0,4,0), B (3,4,2)。
所以 = (0,4,0) , = (-3,0,-2) 。
设点P满足=λ (0≤ λ ≤1),则
= (-3λ,0,-2λ) (0≤ λ ≤1),
所以 = += (-3λ,4,-2λ)
令 =0,得-12λ+12-12λ=0
解得λ=
所以这样的点P存在
当= ,即P为B C中点时, A P∥平面AC D
小结:用向量法解决立体几何问题的步骤
(1)建系.
(2)设点.
(3)表示相关向量
(4)进行向量运算.
(5)把向量运算的结果“翻译”为几何结论.
线面的位置关系 向量的位置关系 向量的运算 向量运算的坐标表示
∥
∥ β
∥
⊥
λ∈R,使得
= =
=0
其中,=(x,y,z), = (, , ), , 是直线l的方向向量; = (, ,), = (, ,), 分别是平面α,β的法向量
+ =0
∥
λ∈R,使得
= =
四、课堂小结
1.能用向量表达空中的点、线和平面.
2. 直线的方向向量和平面的法向量的求解.
3.线线、线面、面面平行关系向量表达.
4. 直线、平面间平行关系的向量法证明.
五、作业布置
课本P29:练习 第2、3题
将几何对象(点、线、面)向量化
用向量方法解决立体几何问题的基础
