12.1函数 同步练习 2022-2023学年沪科版数学八年级上册(无答案)
文档属性
| 名称 | 12.1函数 同步练习 2022-2023学年沪科版数学八年级上册(无答案) | 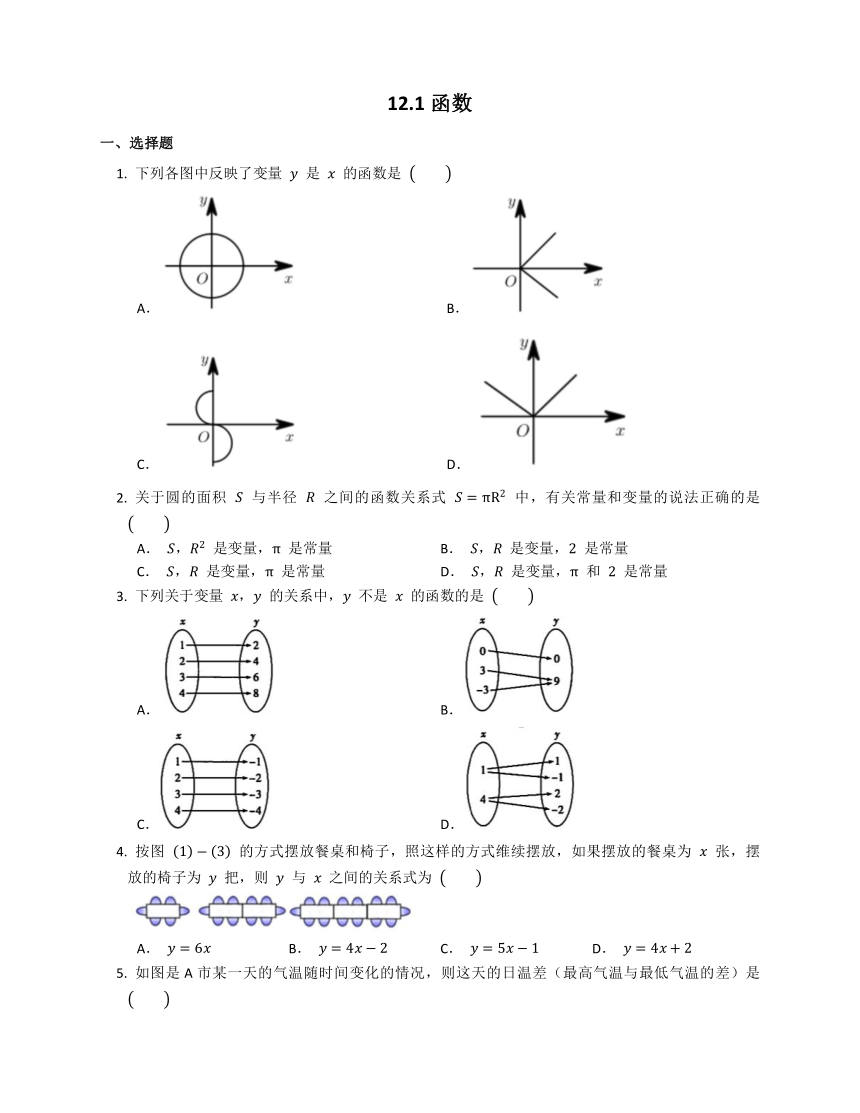 | |
| 格式 | docx | ||
| 文件大小 | 275.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 18:59:07 | ||
图片预览

文档简介
12.1函数
一、选择题
下列各图中反映了变量 是 的函数是
A. B.
C. D.
关于圆的面积 与半径 之间的函数关系式 中,有关常量和变量的说法正确的是
A. , 是变量, 是常量 B. , 是变量, 是常量
C. , 是变量, 是常量 D. , 是变量, 和 是常量
下列关于变量 , 的关系中, 不是 的函数的是
A. B.
C. D.
按图 的方式摆放餐桌和椅子,照这样的方式维续摆放,如果摆放的餐桌为 张,摆放的椅子为 把,则 与 之间的关系式为
A. B. C. D.
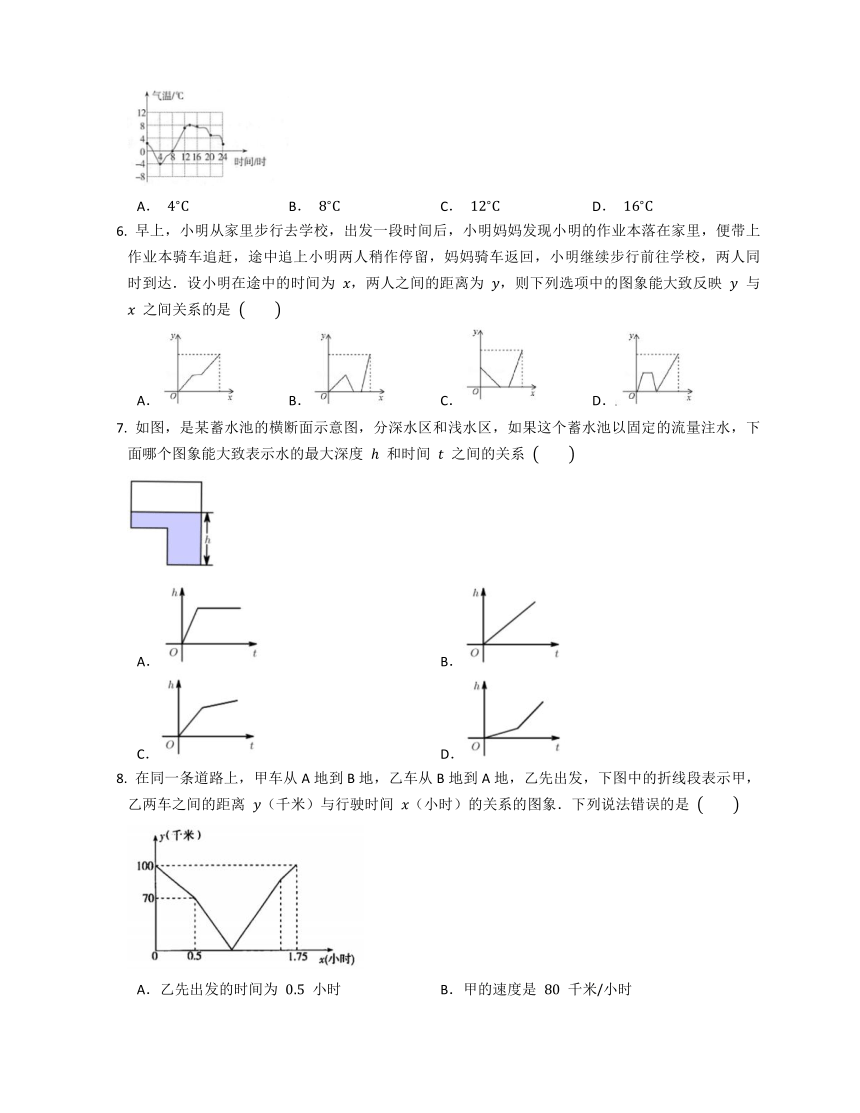
如图是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是
A. B. C. D.
早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途中的时间为 ,两人之间的距离为 ,则下列选项中的图象能大致反映 与 之间关系的是
A. B. C. D.
如图,是某蓄水池的横断面示意图,分深水区和浅水区,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度 和时间 之间的关系
A. B.
C. D.
在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,下图中的折线段表示甲,乙两车之间的距离 (千米)与行驶时间 (小时)的关系的图象.下列说法错误的是
A.乙先出发的时间为 小时 B.甲的速度是 千米/小时
C.甲出发 小时后两车相遇 D.甲到B地比乙到A地早 小时
二、填空题
在 中,底边 的长为 ,边 上的高为 ,面积为 .当面积 一定时, ,在 ,, 中, 是变量, 是常量.
在体积为 的圆柱中,底面积 关于高 的关系式是 ,其中常量是 ,变量是 .
已知函数 ,当自变量 时, ;当函数值 时, .
如图是某人体检时的心电图,其中横坐标 表示时间,纵坐标 表示心脏部位的生物电流,它们是两个变量.在心电图中, (填“是”或“不是”) 的函数.
同一温度的华氏度数 与摄氏度数 之间的函数表达式是 .若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 .
为迎接省运会的召开,市里组织了一个梯形鲜花队参加开幕式,要求共站 排,第一排 人,后面每一排都比前一排多站一人,则每排人数 与该排排数 之间的函数关系式为 .
三、解答题
在平直的路面上,某型号汽车紧急刹车后仍将滑行 ,一般用公式 来计算,其中 表示刹车前汽车的速度(单位:).
(1) 在上述公式中,哪些量是变量,哪些量是常量?
(2) 计算当 分别为 ,, 时,相应的滑行距离 是多少米?
长方形的长是 ,宽是 ,周长是 ,面积是 .
(1) 写出 和 之间的函数解析式;
(2) 写出 与 之间的函数解析式;
(3) 指出自变量 的取值范围.
一个三角形的底边长 ,高 可以任意伸缩.
(1) 写出面积 随 变化的关系式,并指出其中常量与变量.
(2) 分别求出当高 时,对应的面积 的值.
心理学家发现,学生对概念的接受能力 与提出概念所用的时间 (单位:)之间有如下关系:(其中 )
(1) 上表中反映了哪两个变量之间的关系? 是否是 的函数?
(2) 当提出概念所用时间是 时,学生对概念的接受能力是多少?
(3) 根据表格中的数据,你认为提出概念所用的时间为多少时,学生的接受能力最强?
已知有两个人分别骑自行车和摩托车沿着相同的路线从甲地到乙地,下图反映的是这两个人在行驶过程中时间和路程的关系,请根据图象回答下列问题:
(1) 甲地与乙地相距多少千米?两个人分别用了几小时才到达乙地?谁先到达乙地?先到者早到多长时间?
(2) 分别描述在这个过程中自行车和摩托车的行驶状态;
(3) 求摩托车行驶的平均速度.
一、选择题
下列各图中反映了变量 是 的函数是
A. B.
C. D.
关于圆的面积 与半径 之间的函数关系式 中,有关常量和变量的说法正确的是
A. , 是变量, 是常量 B. , 是变量, 是常量
C. , 是变量, 是常量 D. , 是变量, 和 是常量
下列关于变量 , 的关系中, 不是 的函数的是
A. B.
C. D.
按图 的方式摆放餐桌和椅子,照这样的方式维续摆放,如果摆放的餐桌为 张,摆放的椅子为 把,则 与 之间的关系式为
A. B. C. D.
如图是A市某一天的气温随时间变化的情况,则这天的日温差(最高气温与最低气温的差)是
A. B. C. D.
早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途中的时间为 ,两人之间的距离为 ,则下列选项中的图象能大致反映 与 之间关系的是
A. B. C. D.
如图,是某蓄水池的横断面示意图,分深水区和浅水区,如果这个蓄水池以固定的流量注水,下面哪个图象能大致表示水的最大深度 和时间 之间的关系
A. B.
C. D.
在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,下图中的折线段表示甲,乙两车之间的距离 (千米)与行驶时间 (小时)的关系的图象.下列说法错误的是
A.乙先出发的时间为 小时 B.甲的速度是 千米/小时
C.甲出发 小时后两车相遇 D.甲到B地比乙到A地早 小时
二、填空题
在 中,底边 的长为 ,边 上的高为 ,面积为 .当面积 一定时, ,在 ,, 中, 是变量, 是常量.
在体积为 的圆柱中,底面积 关于高 的关系式是 ,其中常量是 ,变量是 .
已知函数 ,当自变量 时, ;当函数值 时, .
如图是某人体检时的心电图,其中横坐标 表示时间,纵坐标 表示心脏部位的生物电流,它们是两个变量.在心电图中, (填“是”或“不是”) 的函数.
同一温度的华氏度数 与摄氏度数 之间的函数表达式是 .若某一温度的摄氏度数值与华氏度数值恰好相等,则此温度的摄氏度数为 .
为迎接省运会的召开,市里组织了一个梯形鲜花队参加开幕式,要求共站 排,第一排 人,后面每一排都比前一排多站一人,则每排人数 与该排排数 之间的函数关系式为 .
三、解答题
在平直的路面上,某型号汽车紧急刹车后仍将滑行 ,一般用公式 来计算,其中 表示刹车前汽车的速度(单位:).
(1) 在上述公式中,哪些量是变量,哪些量是常量?
(2) 计算当 分别为 ,, 时,相应的滑行距离 是多少米?
长方形的长是 ,宽是 ,周长是 ,面积是 .
(1) 写出 和 之间的函数解析式;
(2) 写出 与 之间的函数解析式;
(3) 指出自变量 的取值范围.
一个三角形的底边长 ,高 可以任意伸缩.
(1) 写出面积 随 变化的关系式,并指出其中常量与变量.
(2) 分别求出当高 时,对应的面积 的值.
心理学家发现,学生对概念的接受能力 与提出概念所用的时间 (单位:)之间有如下关系:(其中 )
(1) 上表中反映了哪两个变量之间的关系? 是否是 的函数?
(2) 当提出概念所用时间是 时,学生对概念的接受能力是多少?
(3) 根据表格中的数据,你认为提出概念所用的时间为多少时,学生的接受能力最强?
已知有两个人分别骑自行车和摩托车沿着相同的路线从甲地到乙地,下图反映的是这两个人在行驶过程中时间和路程的关系,请根据图象回答下列问题:
(1) 甲地与乙地相距多少千米?两个人分别用了几小时才到达乙地?谁先到达乙地?先到者早到多长时间?
(2) 分别描述在这个过程中自行车和摩托车的行驶状态;
(3) 求摩托车行驶的平均速度.
