第二十四章 圆 单元复习题 2022-2023学年人教版九年级数学上册(含解析)
文档属性
| 名称 | 第二十四章 圆 单元复习题 2022-2023学年人教版九年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 733.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 19:01:58 | ||
图片预览




文档简介
人教版九年级数学上册第二十四章 圆 单元复习题
一、选择题
1.已知⊙O的直径长为4,点A,B在⊙O上,则AB的长不可能是( )
A.2 B.3 C.4 D.8
2.如图,在中半径与弦垂直于点,且,,则的长是( )
A.1.5 B.2 C.3 D.4
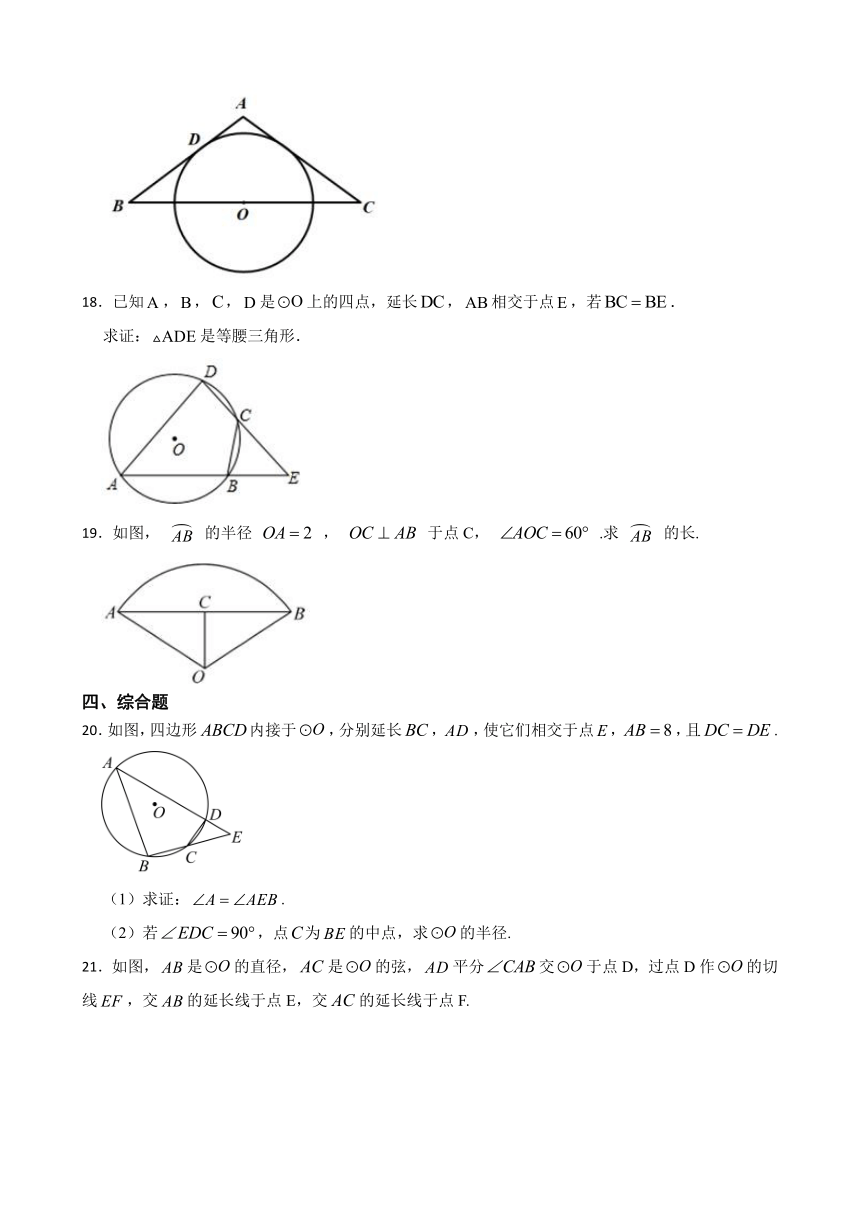
3.下列说法中,正确的是( )
A.长度相等的弧是等弧
B.圆的每一条直径都是它的对称轴
C.直径如果平分弦就一定垂直弦
D.直径所对的弧是半圆
4.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100° C.110° D.120°
5.已知⊙O的半径是5,点P在⊙O内,则OP的长可能是( )
A.4 B.5 C.5.5 D.6
6.如图,为的直径,与相切于点,交的延长线于点,且.若,则半径长为( )
A.2 B.3 C. D.
7.如图,是的直径,弦于点E,连接,若,,则弦的长是( )
A. B. C. D.
8.如图,半径为5的圆O中,弦BC、ED所对的圆心角分别是∠BOC、∠EOD,已知DE=6,∠BOC+∠EOD=180°,则弦BC的弦心距等于( )
A.3 B. C.4 D.
9.如图,一个蜂巢巢房的横截而为正六边形,若对角线的长约为,则正六边形的边长为( )
A. B. C. D.
10.如果一个扇形的圆心角扩大为原来的2倍,半径扩大为原来的3倍,那么这个扇形的面积将扩大为原来的倍数是( )
A.18 B.12 C.6 D.4
二、填空题
11.已知中最长的弦为12厘米,则此圆半径为 厘米.
12.如图,为的直径,点C在上,点Р在线段上运动(不与O,B重合),若,设为,则的取值范围是 .
13.如图,A,B、C三点都在上,,过点A作的切线与的延长线交于点P,则的度数是 .
14.如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为 .
三、解答题
15.如图,已知四边形内接于.求证:.
16.如图,的直径,是的弦,,垂足为M,,求的长.
17.ΔABC为等腰三角形,O为底边BC的中点,腰AB与O相切于点D.
求证:AC是O的切线.
18.已知,,,是上的四点,延长,相交于点,若.
求证:是等腰三角形.
19.如图, 的半径 , 于点C, .求 的长.
四、综合题
20.如图,四边形内接于,分别延长,,使它们相交于点,,且.
(1)求证:.
(2)若,点为的中点,求的半径.
21.如图,是的直径,是的弦,平分交于点D,过点D作的切线,交的延长线于点E,交的延长线于点F.
(1)求证:;
(2)若,求的长.
22.如图,四边形内接于,,是的直径,连接.
(1)求的度数;
(2)若直径为4,求的长.
23.如图,△ABC内接于☉O,∠A=60°,BE⊥AC于点E,延长线交☉O于点P。
(1)如图①,若△ABC是等边三角形,求证:OE=PE;
(2)如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,
①求证:HE=PE
②若BC=3,求点H运动轨迹的长度。
答案解析部分
1.【答案】D
【解析】【解答】解:因为圆中最长的弦为直径,所以0<AB≤4.
观察选项,只有选项D符合题意.
故答案为:D.
【分析】连接圆上任意两点间的线段就是圆的弦,过圆心的弦就是该圆的直径,而圆中最长的弦是直径,据此即可判断得出答案.
2.【答案】C
【解析】【解答】解:∵半径OC与弦AB垂直于点D,,
∴,,
∵,
∴.
故答案为:C.
【分析】根据垂径定理得AD=4,在Rt△OAD中,利用勾股定理算出OD即可.
3.【答案】D
【解析】【解答】解:A、在同圆或等圆中,长度相等的弧是等弧,故A不符合题意;
B、圆的每一条直径所在的直线都是它的对称轴,故B不符合题意;
C、直径平分弦(弦不是直径)就一定垂直于弦,故C不符合题意;
D、直径所对的弧是半圆,故D符合题意.
故答案为:D.
【分析】根据等弧的定义、圆的对称轴、垂径定理、半圆的定义,逐项进行判断,即可得出答案.
4.【答案】C
【解析】【解答】解:∵ AB是⊙O的直径 ,
∴∠ADB=90°,
又∵∠ABD=20°,
∴∠A=90°-∠ABD=70°,
∴∠BCD=180°-∠A=180°-70°=110°.
故答案为:C.
【分析】根据直径所对的圆周角是直角得∠ADB=90°,然后根据直角三角形两锐角互余得∠A的度数,最后根据圆内接四边形的对角互补可求出∠BCD的度数.
5.【答案】A
【解析】【解答】解:设圆的半径为r,点到圆心的距离为d,则r=5,OP=d,
∵ 点P在⊙O内 ,
∴r>d,即OP<5,
所以A选项满足条件.
故答案为:A.
【分析】设圆的半径为r,点到圆心的距离为d,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,据此判断即可得出答案.
6.【答案】B
【解析】【解答】解: 如图,连接,
∵与相切于点,
∴,
∴,
∵,
∴,
∵,
∴,
∵为的直径,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴半径长为3.
故答案为:B.
【分析】连接OC,先证出,再结合可得,求出,再利用含30°角的直角三角形的性质可得,最后求出半径的长即可。
7.【答案】D
【解析】【解答】解:∵
∴
∵
∴
∵
∴
∴.
故答案为:D.
【分析】先求出OB的长,再利用勾股定理求出DE的长,由垂径定理可得CE=DE,根据CD=DE-CE即可求解.
8.【答案】A
【解析】【解答】解:作OH⊥BC于H,延长CO交圆O于点F,连接BF,如图,
∵∠BOC+∠EOD=180°,
而∠BOC+∠BOF=180°,
∴∠DOE=∠BOF,
∴弧DE=弧BF,
∴DE=BF=6,
∵OH⊥BC,
∴CH=BH,
而CO=OF,
∴OH为△CBF的中位线,
∴OH=BF=3.
故答案为:A.
【分析】作OH⊥BC于H,延长CO交圆O于点F,连接BF,先用等角的补角相等得∠DOE=∠BOF,再利用圆心角、弧、弦的关系得到DE=BF=6,由OH⊥BC,根据垂径定理得CH=BH,易得OH为△CBF的中位线,然后根据三角形中位线性质得到OH的长.
9.【答案】C
【解析】【解答】解:如图:连接交于点O,
∵六边形是正六边形,的长约为,
∴,
∵对角线的长约为
∴和约为,
∴约为,
故答案为:C.
【分析】连接BE、CF、BE与CF交于点O,根据正六边形的性质可得∠AOF=60°,OA=OD=OF,推出△AOF为等边三角形,根据AD的值可得OA=OD=5mm,据此解答.
10.【答案】A
【解析】【解答】解:设原扇形的圆心角度数为,半径为,
则:,
圆心角扩大为原来的2倍,半径扩大为原来的3倍后,面积变为:,
∴这个扇形的面积将扩大为原来的18倍;
故答案为:A.
【分析】利用扇形面积公式求解即可。
11.【答案】6
【解析】【解答】解:中最长的弦为12厘米,
的直径为12厘米,
的半径为6厘米.
故答案为:6.
【分析】根据最长的弦是直径可得答案。
12.【答案】
【解析】【解答】解:当点P位于O点时,
,
则,此时的值最小;
当点P位于B点时,根据直径所对的角是可得,此时的值最大;
由于点Р不与O,B重合,
于是.
故答案为:.
【分析】当点P位于O点时,OA=OC,由等腰三角形的性质可得∠CAB=α=30°;当点P位于B点时,根据直径所对的角是90°可得α=∠ACB=90°,据此不难得到α的范围.
13.【答案】20°
【解析】【解答】连接
∵
∴
∵过点A作的切线与的延长线交于点P
∴
∴
故答案为:20°
【分析】连接OA,根据圆周角的性质可得,再根据,利用三角形的内角和求出∠APO的度数即可。
14.【答案】1
【解析】【解答】解:如图,连接AC、BD、OF,
,
已知⊙O的半径是1,
则OF=1,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴OI= ,CI= ,
∴ ,
BD=2,
故GH=1.
【分析】已知⊙O的半径是1,则OF=1,根据AO是∠EAF的平分线,求出∠COF=60°,在Rt△OIF中,求出FI的值是多少;然后判断出OI、CI的关系,再根据GH∥BD,求出GH的值是多少,再用EF的值比上GH的值,求出EF:GH的值是多少即可求GH.
15.【答案】证明:如图,连接,
∵,
∴,
∴.
【解析】【分析】连接OD、OB,由圆周角定理可得∠C=∠BOD,∠A=(360°-∠BOD),据此证明.
16.【答案】解:如图:连接,
的直径,
,
,
,
在中,,
,
的直径为,,
,
故的长为8.
【解析】【分析】连接OA,先利用勾股定理求出AM的长,再利用垂径定理可得。
17.【答案】证明:过点O作OE⊥AC于点E,连结OD,OA,
∵AB与O相切于点D,
∴AB⊥OD,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是O的半径,
∵AC经过O的半径OE的外端点且垂直于OE,
∴AC是O的切线。
【解析】【分析】过点O作OE⊥AC于点E,连结OD,OA,再证明OE=OD,可得OE是O的半径,再结合AC⊥OE,即可得到AC是O的切线。
18.【答案】证明:,,,是上的四点,
,
,
,
,
,即是等腰三角形.
【解析】【分析】根据圆内接四边形的性质可得∠A=∠BCE,由等腰三角形的性质可得∠E=∠BCE,推出∠A=∠E,则DA=DE,据此证明.
19.【答案】解:∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴ 的长为:=.
【解析】【分析】首先由垂径定理结合已知条件可得∠AOB=120°,然后根据弧长公式:计算即可.
20.【答案】(1)证明:∵四边形内接于,
∴,
∵,
∴,
∵
∴,
∴
(2)解:如图,连接
∵,
∴是的直径,
∴,
∵
∴
∵,
∴,
∵点为的中点,
∴,
在中,,
∴的半径为
【解析】【分析】(1)根据圆内接四边形的性质可得∠A+∠BCD=180°,由邻补角的性质可得∠BCD+∠DCE=180°,则∠A=∠DCE,由等腰三角形的性质可得∠E=∠DCE,据此证明;
(2)连接AC,则AC为直径,由圆周角定理可得∠ABC=90°,根据∠A=∠AEB可得AB=BE=8,由中点的概念可得BC的值,然后利用勾股定理进行计算即可.
21.【答案】(1)证明:连接,
∵平分,
∴,
∵,
∴,
∴,
∴,
∵为的切线,
∴,
∴.
(2)解:连结,
∵,
∴为等边三角形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
【解析】【分析】(1)连接OD,根据角平分线的概念可得∠CAD=∠OAD,根据等腰三角形的性质可得∠OAD=∠ODA,则∠CAD=∠ODA,推出OD∥AF,根据切线的性质可得OD⊥EF,据此证明;
(2)连接OC,则△AOC为等边三角形,∠CAE=60°,由平行线的性质可得∠DOE=∠CAE=60°,则∠E=90°-∠DOE=30°,根据含30°角的直角三角形的性质可得OE=2OD=4,然后根据BE=OE-OB进行计算.
22.【答案】(1)解:∵四边形内接于,
∴,
∵,
∴;
(2)解:连接,
由圆周角定理得:,
∵是的直径,
∴,
∴,
∴
∴.
【解析】【分析】(1)利用圆内接四边形的性质可得,再结合,求出即可;
(2)连接BE,先求出,利用含30°角的直角三角形的性质求出,最后利用勾股定理求出BD的长即可。
23.【答案】(1)证明:如图所示,连接OC,PC,
∵△ABC是等边三角形,
∴∠BAC=60°
∴∠BPC=∠BAC=60° ,
∵圆O是△ABC的外接圆,
∴圆O是△ABCC三边的垂直平分线的交点,
∴∠BAC是等边三角形,BE⊥AC,
∴BE 在线段AC的垂直平分线上,
∴O在线段BP上,
∴ ,
∴ 是等边三角形,
∵ ,
∴
(2)解:①如图所示,连接PC,
同理可得 ,
∵
∴
∴ =30°,
又 ∵ ,
∴ ,
∴ ,
∴ 是等边三角形,
∴ HE=PE ;
②由①得 ,
∴
∵
∴H是在以 B C为弦,圆周角 的圆上运动,
如图所示,劣弧 即为H的运动轨迹,过点 作 于 ,
∴
∵
∴
∴
∴
∴
∵ ,
∴ ,
∴
∴.
【解析】【分析】(1)连接OC,PC,证出△OPC是等边三角形,再根据等边三角形的性质即可得出OE=PE;
(2)①连接PC,证出△CPH是等边三角形,再根据等边三角形的性质即可得出OHE=PE;
②根据题意得出H是在以BC为弦,圆周角的圆上运动,从而得出劣弧 即为H的运动轨迹,利用弧长公式求出的长度,即可得出答案.
一、选择题
1.已知⊙O的直径长为4,点A,B在⊙O上,则AB的长不可能是( )
A.2 B.3 C.4 D.8
2.如图,在中半径与弦垂直于点,且,,则的长是( )
A.1.5 B.2 C.3 D.4
3.下列说法中,正确的是( )
A.长度相等的弧是等弧
B.圆的每一条直径都是它的对称轴
C.直径如果平分弦就一定垂直弦
D.直径所对的弧是半圆
4.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD=20°,则∠BCD的度数是( )
A.90° B.100° C.110° D.120°
5.已知⊙O的半径是5,点P在⊙O内,则OP的长可能是( )
A.4 B.5 C.5.5 D.6
6.如图,为的直径,与相切于点,交的延长线于点,且.若,则半径长为( )
A.2 B.3 C. D.
7.如图,是的直径,弦于点E,连接,若,,则弦的长是( )
A. B. C. D.
8.如图,半径为5的圆O中,弦BC、ED所对的圆心角分别是∠BOC、∠EOD,已知DE=6,∠BOC+∠EOD=180°,则弦BC的弦心距等于( )
A.3 B. C.4 D.
9.如图,一个蜂巢巢房的横截而为正六边形,若对角线的长约为,则正六边形的边长为( )
A. B. C. D.
10.如果一个扇形的圆心角扩大为原来的2倍,半径扩大为原来的3倍,那么这个扇形的面积将扩大为原来的倍数是( )
A.18 B.12 C.6 D.4
二、填空题
11.已知中最长的弦为12厘米,则此圆半径为 厘米.
12.如图,为的直径,点C在上,点Р在线段上运动(不与O,B重合),若,设为,则的取值范围是 .
13.如图,A,B、C三点都在上,,过点A作的切线与的延长线交于点P,则的度数是 .
14.如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为 .
三、解答题
15.如图,已知四边形内接于.求证:.
16.如图,的直径,是的弦,,垂足为M,,求的长.
17.ΔABC为等腰三角形,O为底边BC的中点,腰AB与O相切于点D.
求证:AC是O的切线.
18.已知,,,是上的四点,延长,相交于点,若.
求证:是等腰三角形.
19.如图, 的半径 , 于点C, .求 的长.
四、综合题
20.如图,四边形内接于,分别延长,,使它们相交于点,,且.
(1)求证:.
(2)若,点为的中点,求的半径.
21.如图,是的直径,是的弦,平分交于点D,过点D作的切线,交的延长线于点E,交的延长线于点F.
(1)求证:;
(2)若,求的长.
22.如图,四边形内接于,,是的直径,连接.
(1)求的度数;
(2)若直径为4,求的长.
23.如图,△ABC内接于☉O,∠A=60°,BE⊥AC于点E,延长线交☉O于点P。
(1)如图①,若△ABC是等边三角形,求证:OE=PE;
(2)如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,
①求证:HE=PE
②若BC=3,求点H运动轨迹的长度。
答案解析部分
1.【答案】D
【解析】【解答】解:因为圆中最长的弦为直径,所以0<AB≤4.
观察选项,只有选项D符合题意.
故答案为:D.
【分析】连接圆上任意两点间的线段就是圆的弦,过圆心的弦就是该圆的直径,而圆中最长的弦是直径,据此即可判断得出答案.
2.【答案】C
【解析】【解答】解:∵半径OC与弦AB垂直于点D,,
∴,,
∵,
∴.
故答案为:C.
【分析】根据垂径定理得AD=4,在Rt△OAD中,利用勾股定理算出OD即可.
3.【答案】D
【解析】【解答】解:A、在同圆或等圆中,长度相等的弧是等弧,故A不符合题意;
B、圆的每一条直径所在的直线都是它的对称轴,故B不符合题意;
C、直径平分弦(弦不是直径)就一定垂直于弦,故C不符合题意;
D、直径所对的弧是半圆,故D符合题意.
故答案为:D.
【分析】根据等弧的定义、圆的对称轴、垂径定理、半圆的定义,逐项进行判断,即可得出答案.
4.【答案】C
【解析】【解答】解:∵ AB是⊙O的直径 ,
∴∠ADB=90°,
又∵∠ABD=20°,
∴∠A=90°-∠ABD=70°,
∴∠BCD=180°-∠A=180°-70°=110°.
故答案为:C.
【分析】根据直径所对的圆周角是直角得∠ADB=90°,然后根据直角三角形两锐角互余得∠A的度数,最后根据圆内接四边形的对角互补可求出∠BCD的度数.
5.【答案】A
【解析】【解答】解:设圆的半径为r,点到圆心的距离为d,则r=5,OP=d,
∵ 点P在⊙O内 ,
∴r>d,即OP<5,
所以A选项满足条件.
故答案为:A.
【分析】设圆的半径为r,点到圆心的距离为d,当d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内,据此判断即可得出答案.
6.【答案】B
【解析】【解答】解: 如图,连接,
∵与相切于点,
∴,
∴,
∵,
∴,
∵,
∴,
∵为的直径,
∴,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴半径长为3.
故答案为:B.
【分析】连接OC,先证出,再结合可得,求出,再利用含30°角的直角三角形的性质可得,最后求出半径的长即可。
7.【答案】D
【解析】【解答】解:∵
∴
∵
∴
∵
∴
∴.
故答案为:D.
【分析】先求出OB的长,再利用勾股定理求出DE的长,由垂径定理可得CE=DE,根据CD=DE-CE即可求解.
8.【答案】A
【解析】【解答】解:作OH⊥BC于H,延长CO交圆O于点F,连接BF,如图,
∵∠BOC+∠EOD=180°,
而∠BOC+∠BOF=180°,
∴∠DOE=∠BOF,
∴弧DE=弧BF,
∴DE=BF=6,
∵OH⊥BC,
∴CH=BH,
而CO=OF,
∴OH为△CBF的中位线,
∴OH=BF=3.
故答案为:A.
【分析】作OH⊥BC于H,延长CO交圆O于点F,连接BF,先用等角的补角相等得∠DOE=∠BOF,再利用圆心角、弧、弦的关系得到DE=BF=6,由OH⊥BC,根据垂径定理得CH=BH,易得OH为△CBF的中位线,然后根据三角形中位线性质得到OH的长.
9.【答案】C
【解析】【解答】解:如图:连接交于点O,
∵六边形是正六边形,的长约为,
∴,
∵对角线的长约为
∴和约为,
∴约为,
故答案为:C.
【分析】连接BE、CF、BE与CF交于点O,根据正六边形的性质可得∠AOF=60°,OA=OD=OF,推出△AOF为等边三角形,根据AD的值可得OA=OD=5mm,据此解答.
10.【答案】A
【解析】【解答】解:设原扇形的圆心角度数为,半径为,
则:,
圆心角扩大为原来的2倍,半径扩大为原来的3倍后,面积变为:,
∴这个扇形的面积将扩大为原来的18倍;
故答案为:A.
【分析】利用扇形面积公式求解即可。
11.【答案】6
【解析】【解答】解:中最长的弦为12厘米,
的直径为12厘米,
的半径为6厘米.
故答案为:6.
【分析】根据最长的弦是直径可得答案。
12.【答案】
【解析】【解答】解:当点P位于O点时,
,
则,此时的值最小;
当点P位于B点时,根据直径所对的角是可得,此时的值最大;
由于点Р不与O,B重合,
于是.
故答案为:.
【分析】当点P位于O点时,OA=OC,由等腰三角形的性质可得∠CAB=α=30°;当点P位于B点时,根据直径所对的角是90°可得α=∠ACB=90°,据此不难得到α的范围.
13.【答案】20°
【解析】【解答】连接
∵
∴
∵过点A作的切线与的延长线交于点P
∴
∴
故答案为:20°
【分析】连接OA,根据圆周角的性质可得,再根据,利用三角形的内角和求出∠APO的度数即可。
14.【答案】1
【解析】【解答】解:如图,连接AC、BD、OF,
,
已知⊙O的半径是1,
则OF=1,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴OI= ,CI= ,
∴ ,
BD=2,
故GH=1.
【分析】已知⊙O的半径是1,则OF=1,根据AO是∠EAF的平分线,求出∠COF=60°,在Rt△OIF中,求出FI的值是多少;然后判断出OI、CI的关系,再根据GH∥BD,求出GH的值是多少,再用EF的值比上GH的值,求出EF:GH的值是多少即可求GH.
15.【答案】证明:如图,连接,
∵,
∴,
∴.
【解析】【分析】连接OD、OB,由圆周角定理可得∠C=∠BOD,∠A=(360°-∠BOD),据此证明.
16.【答案】解:如图:连接,
的直径,
,
,
,
在中,,
,
的直径为,,
,
故的长为8.
【解析】【分析】连接OA,先利用勾股定理求出AM的长,再利用垂径定理可得。
17.【答案】证明:过点O作OE⊥AC于点E,连结OD,OA,
∵AB与O相切于点D,
∴AB⊥OD,
∵△ABC为等腰三角形,O是底边BC的中点,
∴AO是∠BAC的平分线,
∴OE=OD,即OE是O的半径,
∵AC经过O的半径OE的外端点且垂直于OE,
∴AC是O的切线。
【解析】【分析】过点O作OE⊥AC于点E,连结OD,OA,再证明OE=OD,可得OE是O的半径,再结合AC⊥OE,即可得到AC是O的切线。
18.【答案】证明:,,,是上的四点,
,
,
,
,
,即是等腰三角形.
【解析】【分析】根据圆内接四边形的性质可得∠A=∠BCE,由等腰三角形的性质可得∠E=∠BCE,推出∠A=∠E,则DA=DE,据此证明.
19.【答案】解:∵OC⊥AB,∠AOC=60°,
∴∠AOB=120°.
∵OA=2,
∴ 的长为:=.
【解析】【分析】首先由垂径定理结合已知条件可得∠AOB=120°,然后根据弧长公式:计算即可.
20.【答案】(1)证明:∵四边形内接于,
∴,
∵,
∴,
∵
∴,
∴
(2)解:如图,连接
∵,
∴是的直径,
∴,
∵
∴
∵,
∴,
∵点为的中点,
∴,
在中,,
∴的半径为
【解析】【分析】(1)根据圆内接四边形的性质可得∠A+∠BCD=180°,由邻补角的性质可得∠BCD+∠DCE=180°,则∠A=∠DCE,由等腰三角形的性质可得∠E=∠DCE,据此证明;
(2)连接AC,则AC为直径,由圆周角定理可得∠ABC=90°,根据∠A=∠AEB可得AB=BE=8,由中点的概念可得BC的值,然后利用勾股定理进行计算即可.
21.【答案】(1)证明:连接,
∵平分,
∴,
∵,
∴,
∴,
∴,
∵为的切线,
∴,
∴.
(2)解:连结,
∵,
∴为等边三角形,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴.
【解析】【分析】(1)连接OD,根据角平分线的概念可得∠CAD=∠OAD,根据等腰三角形的性质可得∠OAD=∠ODA,则∠CAD=∠ODA,推出OD∥AF,根据切线的性质可得OD⊥EF,据此证明;
(2)连接OC,则△AOC为等边三角形,∠CAE=60°,由平行线的性质可得∠DOE=∠CAE=60°,则∠E=90°-∠DOE=30°,根据含30°角的直角三角形的性质可得OE=2OD=4,然后根据BE=OE-OB进行计算.
22.【答案】(1)解:∵四边形内接于,
∴,
∵,
∴;
(2)解:连接,
由圆周角定理得:,
∵是的直径,
∴,
∴,
∴
∴.
【解析】【分析】(1)利用圆内接四边形的性质可得,再结合,求出即可;
(2)连接BE,先求出,利用含30°角的直角三角形的性质求出,最后利用勾股定理求出BD的长即可。
23.【答案】(1)证明:如图所示,连接OC,PC,
∵△ABC是等边三角形,
∴∠BAC=60°
∴∠BPC=∠BAC=60° ,
∵圆O是△ABC的外接圆,
∴圆O是△ABCC三边的垂直平分线的交点,
∴∠BAC是等边三角形,BE⊥AC,
∴BE 在线段AC的垂直平分线上,
∴O在线段BP上,
∴ ,
∴ 是等边三角形,
∵ ,
∴
(2)解:①如图所示,连接PC,
同理可得 ,
∵
∴
∴ =30°,
又 ∵ ,
∴ ,
∴ ,
∴ 是等边三角形,
∴ HE=PE ;
②由①得 ,
∴
∵
∴H是在以 B C为弦,圆周角 的圆上运动,
如图所示,劣弧 即为H的运动轨迹,过点 作 于 ,
∴
∵
∴
∴
∴
∴
∵ ,
∴ ,
∴
∴.
【解析】【分析】(1)连接OC,PC,证出△OPC是等边三角形,再根据等边三角形的性质即可得出OE=PE;
(2)①连接PC,证出△CPH是等边三角形,再根据等边三角形的性质即可得出OHE=PE;
②根据题意得出H是在以BC为弦,圆周角的圆上运动,从而得出劣弧 即为H的运动轨迹,利用弧长公式求出的长度,即可得出答案.
同课章节目录
