弦.弦心距.圆心角的关系[下学期]
图片预览







文档简介
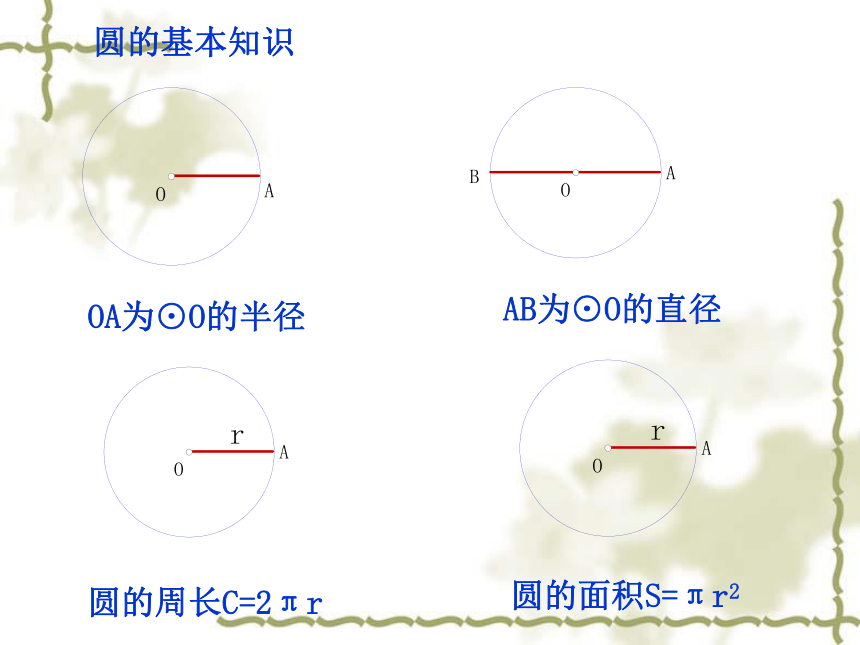
课件49张PPT。圆OA为⊙O的半径AB为⊙O的直径圆的周长C=2πr圆的面积S=πr2圆的基本知识操作:
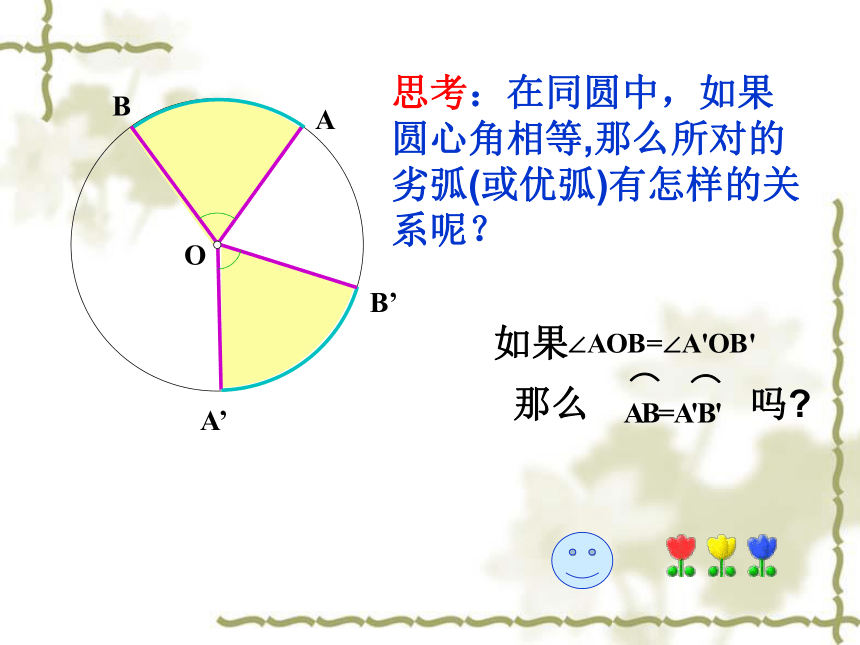
让一个圆绕圆心旋转任意角度, 都能和原来图形重合吗?O 一个圆绕着它的圆心旋转任意一个角度,都能与原来图形重合OOA’B’AB思考:在同圆中,如果圆心角相等,那么所对的劣弧(或优弧)有怎样的关系呢?如果那么 吗?所对的劣弧(或优弧)相等,所对的弦相等,所对的弦的弦心距相等。我们把能够重合的两个圆称为等圆,那么在等圆中,上述结论成立吗?圆的性质:
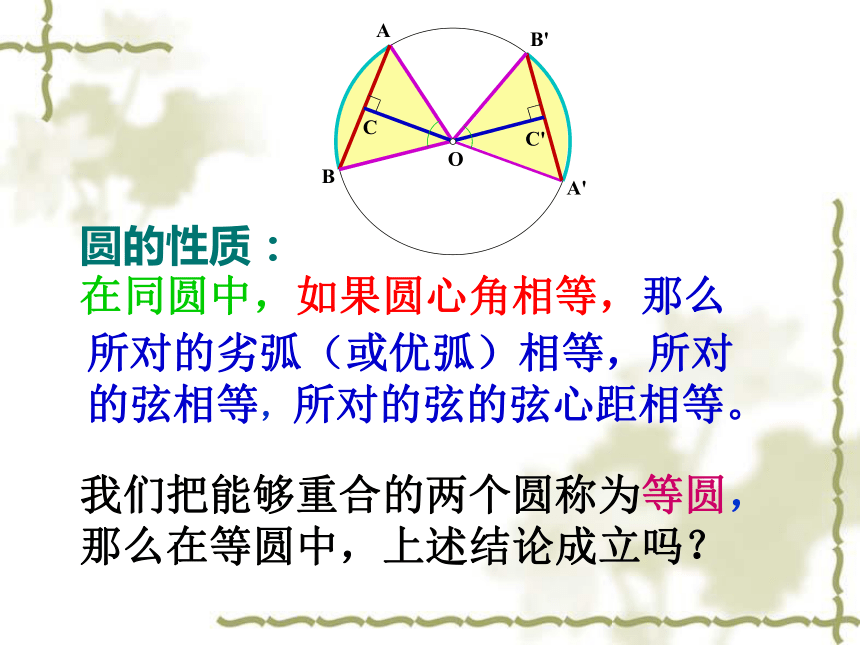
在同圆中,如果圆心角相等,那么圆的性质:
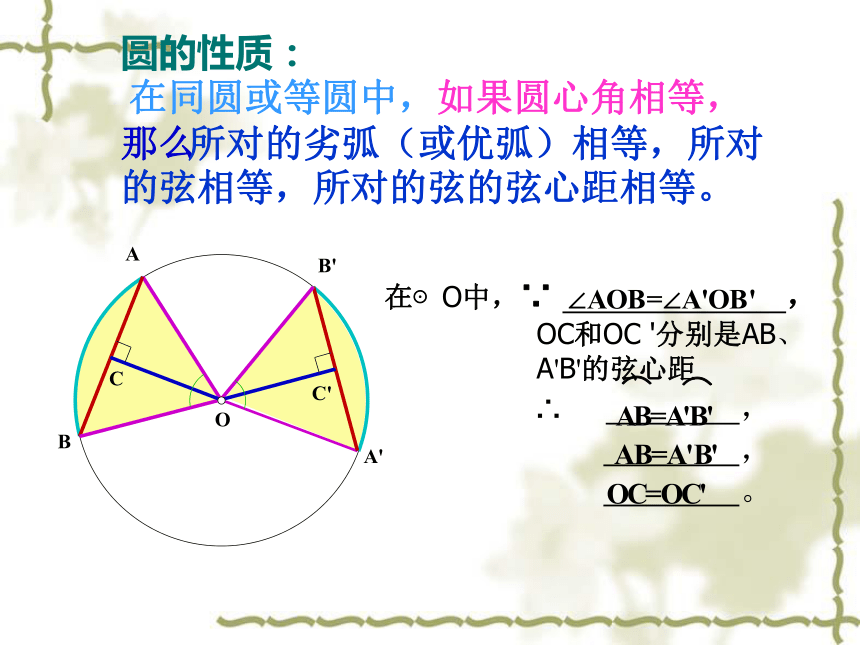
在同圆或等圆中,如果圆心角相等,那么 ∴ ,
,
。
在⊙O中,∵ ,
OC和OC '分别是AB、
A'B'的弦心距
所对的劣弧(或优弧)相等,所对的弦相等,所对的弦的弦心距相等。
在同圆或等圆中,
(1) 如果已知两条劣弧(或优弧)相等,你能得出
什么结论呢?
(2) 如果已知两条弦相等,你能得出什么结论呢?
(3) 如果已知两条弦心距相等,你能得出什么结论
呢?讨 论 圆心角、弧、 弦、弦心距 之间的关系(1)在同圆或等圆中,如果圆心角相等,那么所对的劣弧(或优弧)相等,所对的弦相等,所对的弦心距相等。
(2)在同圆或等圆中,如果弧相等,那么所对的圆心角相等,所对的弦相等,弦的弦心距相等。
(3)在同圆或等圆中,如果弦相等, 那么所对的劣弧(或优弧)相等,所对的圆心角相等,所对的弦心距相等。
(4)在同圆或等圆中,如果弦心距相等,那么所对的弦相等,弦所对的劣弧(或优弧)相等,所对的圆心角相等。
在同圆或等圆中(圆心角、弧、弦、弦心距)
条件 结论
1、圆心角相等 弧、 弦、弦心距相等
2、弧相等 圆心角、 弦、弦心距相等
3、弦相等 圆心角、 弧、 弦心距相等
4、弦心距相等 圆心角 、 弧、 弦相等
在同圆或等圆中,如果两个圆心角、两条弧、 两条弦或两条弦的弦心距这四组量中有一组量相等,那么它们所对应的其余三组量也分别相等。(一推三)
注意:前提在同圆或等圆中判断题(1)因为∠AOB= ∠A’OB’,
所以AB=A’B’
(2)在⊙O和⊙O’中,OC和OC’是AB和A’B’的弦心距
如果AB= A’ B’,
那么OC=O’C’(╳)(╳)巩固应用OA'AB'B在同圆或等圆中,
如果 弧相等,
那么 所对的圆心角相等,所对的
弦相等,弦的弦心距相等。
∴ ,
,
。
在⊙O中∵ ,
⌒⌒ AB=A'B'
OC和OC'分别是AB、
A'B'的弦心距(已知)
AB=A'B' ∠AOB= ∠A'OB' OC=OC'
那么 所对的劣弧(或优弧)相
等, 所对的圆心角相等,所
对的弦心距相等。
ABOCA'B'C' ∴ ,
,
。
在⊙O中,∵ ,
⌒⌒AB=A'B'AB=A'B’,
OC和OC'分别是AB、A'B'的弦心距(已知)
∠AOB= ∠A'OB'OC=OC'在同圆或等圆中,
如果 弦相等,
那么 所对的弦相等,弦所对的劣
弧(或优弧)相等,所对的
圆心角相等。
ABOCA'B'C' ∴ ,
,
。
在⊙O中,∵ ,
⌒⌒AB=A'B'
OC和OC'分别是AB、A'B'的弦心距(已知)
∠AOB= ∠A'OB'OC=OC'在同圆或等圆中,
如果 弦心距相等,AB=A'B',例1 如图,⊙O中,AB=CD,OE、OF分别是AB、CD的弦心距。(2)OE和OF相等吗?为什么?例题精选⌒⌒解:
(1)∵AB=CD(已知),
∴AB=CD(同圆中,如果弧相等,那么所对的弦相等)。
⌒⌒(2)∵AB=CD,OE、OF分别是AB、CD的弦心距(已知)
∴OE=OF(同圆中,如果弧相等,那么所对的弦心距相等)。⌒⌒(3)如果已知改为AC=BD,能得到以
上结论吗?⌒⌒(1)∠B与∠C相等吗?为什么?(2) OD和OE是AB、BC的弦心距,若OD=OE,请问△ABC是什么
三角形?∠A、∠B、∠C为多少度?为什么?解 ∵OD=OE(已知)
∴AB=BC(同圆中,如果弦心距相等,那么所对的弦相等)。
又∵AB=AC(已证)
∴AB=AC=BC(等量代换)
∴△ABC是等边三角形(三条边都相等的三角形是等边三角形)。
∴∠A=∠B=∠C=60度(等边三角形的每个内角都等于60度)。⌒⌒oEDCBA如图,AB,CD是⊙O的两条弦,OE,OF为AB、CD的弦心距。你能添加什么条件,使得∠AOB=∠COD?
BAOECDF∵ OE = OF, OE,OF为AB、CD的弦心距(已知)
∴ ∠AOB=∠COD(同圆中,如果弦心距相等,
那么所对的圆心角相等)∵ AB = CD(已知)
∴ ∠AOB=∠COD(同圆中,如果弦相等,
那么所对的圆心角相等)
∵ AB = CD(已知)
∴ ∠AOB=∠COD(同圆中,如果弧相等,
那么所对的圆心角相等)⌒⌒抢答解 ∵OC=OD( ),
∴ ( )。 ∵ (已知)
∴∠D=∠3( ),
∠C=∠1( )。∵∠2=∠1( ),
∴∠2=∠1=∠BOD(等量代换)。⌒⌒⌒同圆的半径相等等边对等角CD∥AB两直线平行,内错角相等两直线平行,内错角相等对顶角相等∠C=∠D 同圆中,如果圆心角相等 ,那么所对的劣弧(或优弧)相等思考与提高 折折剪剪:你能利用今天所学的知识将一个圆面用剪刀剪成一个边长相等的八边形吗?思考:在同圆中,如果圆心角扩大2倍,那么所对的弧,所对的弦怎样变化呢?
ABCO12小结
1.这节课学习了哪些具体内容?
(1)弦、弦心距、半圆、优弧、劣弧、等圆的概念
(2)圆的性质:在同圆或等圆中,如果两个圆心角、
两条劣弧(或优弧)、两条弦或两条弦的弦心距,
这四组量中有一组量相等,那么它们所对应的其
余三组量也分别相等。下课啦!谢谢各位老师的光临!作业:1. 课本第80页练习1和3
2. A册习题16.2
一、教材分析 在学习本节课前,学生已经掌握了圆的一些基本知识和旋转的有关概念。这节课有关圆的性质是今后进一步学习圆的必不可少的基础。二、教学目标 1.理解弦、弦心距、半圆、优弧、劣弧、等圆的概念;
2.掌握在同圆或等圆中,圆心角、弧、 弦、弦心距之
间的关系,并初步学会运用这些关系解决有关问题;
3.通过操作和多媒体演示,培养学生观察、分析、归
纳的能力,向学生渗透旋转变换的思想及由特殊到一
般的认识规律 。 三、教学重点和难点 重点:在同圆或等圆中,圆心角、弧、弦、
弦心距之间的关系;
难点:推出在同圆或等圆中圆心角、弧
弦、弦心距之间的关系。
四、教学准备 用硬纸板做两个圆,大头针,尺,多媒体课件,电脑五、教学过程设计 (一)、创设情景,引入新课
1、复习旧知:圆的半径、直径、周长公式、面积公式等知识。
2.操作:让⊙O绕圆心旋转任意角度,观察发现什么结论。
结论:圆不论绕圆心旋转多少度,都能够和原来的图形重合。(用flash)
3、用旋转的角度复习圆心角概念(半径绕圆心旋转),引出弧(半圆、优弧、劣弧)(动点A绕圆心旋转)、弦、弦心距的概念。(用几何画板,这是对有关概念的动态认识)
把圆心角,弧、弦、弦心距的概念和圆的旋转联系起来。使概念形象化,孕伏了“轨迹”的思想。
这节课我们就来研究在同圆或等圆中圆心角及所对的弧、弦、弦的弦心距之间的关系(引出课题)
(二)、大胆猜想,发现性质 1、在⊙O中,再画圆心角∠A′OB′,使∠AOB=∠A′OB′
再作出它们所对的弦AB,A′B′和弦的弦心距OM,OM′
猜想,其余三组量∠AOB=∠A′OB′所对的弧、弦、弦心
距的大小关系如何?为什么?(用几何画板,教师边演示,边
启发学生得出结论)
简单的猜想和多媒体演示得出圆的性质,使学生产
生学习的兴趣和自信心。直观,易懂,激发学生积
极思考。
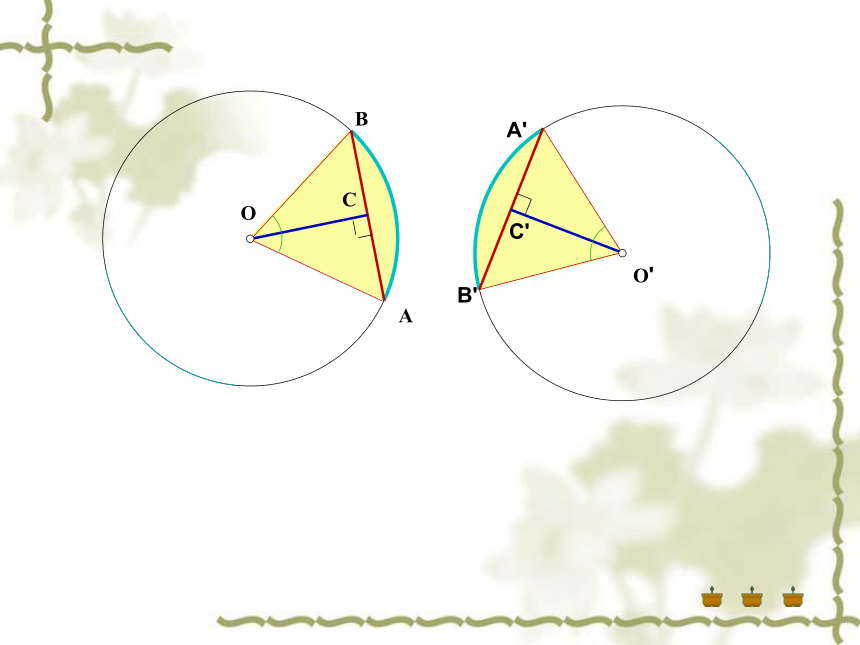
2、在等圆中呢?(用两圆叠合)
3、圆的性质:在同圆或等圆中,如果圆心角相等,那么所对的劣弧(或优弧)相等,所对的弦相等,所对的弦的弦心距相等。
性质的条件和结论分别是什么?并用符号语言表示。
在教学中,重点突破第一条性质。通过第一条性质的突破,使学生提高观察分析、归纳能力。以学生为主体,从而突破本节课的难点。
4、思考,在同圆或等圆中,把圆心角相等与三个结论中的任何一个交换位置,可以得到三个新的结论,这三个结论正确吗?简单说明为什么。判断题(1)因为∠AOB= ∠A’OB’,
所以AB=A’B’
(2)在⊙O和⊙O’中,OC和OC’是AB和A’B’的弦心距
如果∠AOB= ∠A’OB’,
那么OC=O’C’(╳)(╳)(三)、巩固应用、变式练习强调前提在同圆或等圆中.提问中差学生,调动学习积极性,培养学习兴趣,增强自信心。例1 如图,⊙O中,AB=CD,OE、OF分别是AB、CD的弦心距。(2)OE和OF相等吗?为什么?⌒⌒(四)、例题精选DBCoAEF这题以口答形式,使学生对新知灵活应用,利用所学知识进行简单说理。(1)∠B与∠C相等吗?为什么?(2) OD和OE是AB、BC的弦心距,若OD=OE,请问△ABC是什么三角形?∠A、∠B、∠C为多少度?为什么?⌒⌒oEDCBA这题让学生书写 。
巩固并熟悉新知,并能简单说理。 抢答题
AB,CD是⊙O的两条弦,OE,OF为AB、CD的弦心距。你能添加什么条件,使得∠AOB=∠COD?
通过开放性提问,熟悉圆的性质中条件和结论的准确应用。(1)∵ (已知)
∴∠AOB=∠COD(同圆中,如果弧相等,那么所对的圆
心角相等)
(2)∵ AB=CD(已知)
∴∠AOB=∠COD(同圆中,如果弦相等,那么所对的圆
心角相等)
(3)∵OE=OF, OE,OF为AB、CD的弦心距(已知)
∴ ∠AOB=∠COD(同圆中,如果弦心距相等,那么所
对的圆心角相等)⌒⌒⌒这题用填空形式。能应用圆的性质简单说理 。五、思考与提高 折折剪剪:你能利用今天所学的知识将一个圆面用剪刀剪成一个边长相等的八边形吗?八等分后折成的扇形用剪刀把它剪成三角形,则展开后是什么图形?为什么?
通过生活中的实际问题,让学生操作,激发学生学习数学的积极性,对所学知识巩固、提高。
2、思考:在同圆中,如果圆心角扩大2倍,那么所对的弧,所对的弦怎样变化呢?
ABCO12
(六)师生共同小结
(1)弦、弦心距、半圆、优弧、劣弧、等圆的概念
(2)在同圆或等圆中,如果两个圆心角、两条劣弧(或优
弧)、两条弦或两条弦的弦心距,这四组量中有一组
量相等,那么它们所对应的其余三组量也分别相等。
(3)注意前提条件 “在同圆或等圆中”
(七)布置作业
1. 课本第80页练习1和3
2. A册习题16.2 六、教学说明教学形式:多媒体辅助教学
教材结构设计:引入问题—探索分析—归纳—结论—应用
让一个圆绕圆心旋转任意角度, 都能和原来图形重合吗?O 一个圆绕着它的圆心旋转任意一个角度,都能与原来图形重合OOA’B’AB思考:在同圆中,如果圆心角相等,那么所对的劣弧(或优弧)有怎样的关系呢?如果那么 吗?所对的劣弧(或优弧)相等,所对的弦相等,所对的弦的弦心距相等。我们把能够重合的两个圆称为等圆,那么在等圆中,上述结论成立吗?圆的性质:
在同圆中,如果圆心角相等,那么圆的性质:
在同圆或等圆中,如果圆心角相等,那么 ∴ ,
,
。
在⊙O中,∵ ,
OC和OC '分别是AB、
A'B'的弦心距
所对的劣弧(或优弧)相等,所对的弦相等,所对的弦的弦心距相等。
在同圆或等圆中,
(1) 如果已知两条劣弧(或优弧)相等,你能得出
什么结论呢?
(2) 如果已知两条弦相等,你能得出什么结论呢?
(3) 如果已知两条弦心距相等,你能得出什么结论
呢?讨 论 圆心角、弧、 弦、弦心距 之间的关系(1)在同圆或等圆中,如果圆心角相等,那么所对的劣弧(或优弧)相等,所对的弦相等,所对的弦心距相等。
(2)在同圆或等圆中,如果弧相等,那么所对的圆心角相等,所对的弦相等,弦的弦心距相等。
(3)在同圆或等圆中,如果弦相等, 那么所对的劣弧(或优弧)相等,所对的圆心角相等,所对的弦心距相等。
(4)在同圆或等圆中,如果弦心距相等,那么所对的弦相等,弦所对的劣弧(或优弧)相等,所对的圆心角相等。
在同圆或等圆中(圆心角、弧、弦、弦心距)
条件 结论
1、圆心角相等 弧、 弦、弦心距相等
2、弧相等 圆心角、 弦、弦心距相等
3、弦相等 圆心角、 弧、 弦心距相等
4、弦心距相等 圆心角 、 弧、 弦相等
在同圆或等圆中,如果两个圆心角、两条弧、 两条弦或两条弦的弦心距这四组量中有一组量相等,那么它们所对应的其余三组量也分别相等。(一推三)
注意:前提在同圆或等圆中判断题(1)因为∠AOB= ∠A’OB’,
所以AB=A’B’
(2)在⊙O和⊙O’中,OC和OC’是AB和A’B’的弦心距
如果AB= A’ B’,
那么OC=O’C’(╳)(╳)巩固应用OA'AB'B在同圆或等圆中,
如果 弧相等,
那么 所对的圆心角相等,所对的
弦相等,弦的弦心距相等。
∴ ,
,
。
在⊙O中∵ ,
⌒⌒ AB=A'B'
OC和OC'分别是AB、
A'B'的弦心距(已知)
AB=A'B' ∠AOB= ∠A'OB' OC=OC'
那么 所对的劣弧(或优弧)相
等, 所对的圆心角相等,所
对的弦心距相等。
ABOCA'B'C' ∴ ,
,
。
在⊙O中,∵ ,
⌒⌒AB=A'B'AB=A'B’,
OC和OC'分别是AB、A'B'的弦心距(已知)
∠AOB= ∠A'OB'OC=OC'在同圆或等圆中,
如果 弦相等,
那么 所对的弦相等,弦所对的劣
弧(或优弧)相等,所对的
圆心角相等。
ABOCA'B'C' ∴ ,
,
。
在⊙O中,∵ ,
⌒⌒AB=A'B'
OC和OC'分别是AB、A'B'的弦心距(已知)
∠AOB= ∠A'OB'OC=OC'在同圆或等圆中,
如果 弦心距相等,AB=A'B',例1 如图,⊙O中,AB=CD,OE、OF分别是AB、CD的弦心距。(2)OE和OF相等吗?为什么?例题精选⌒⌒解:
(1)∵AB=CD(已知),
∴AB=CD(同圆中,如果弧相等,那么所对的弦相等)。
⌒⌒(2)∵AB=CD,OE、OF分别是AB、CD的弦心距(已知)
∴OE=OF(同圆中,如果弧相等,那么所对的弦心距相等)。⌒⌒(3)如果已知改为AC=BD,能得到以
上结论吗?⌒⌒(1)∠B与∠C相等吗?为什么?(2) OD和OE是AB、BC的弦心距,若OD=OE,请问△ABC是什么
三角形?∠A、∠B、∠C为多少度?为什么?解 ∵OD=OE(已知)
∴AB=BC(同圆中,如果弦心距相等,那么所对的弦相等)。
又∵AB=AC(已证)
∴AB=AC=BC(等量代换)
∴△ABC是等边三角形(三条边都相等的三角形是等边三角形)。
∴∠A=∠B=∠C=60度(等边三角形的每个内角都等于60度)。⌒⌒oEDCBA如图,AB,CD是⊙O的两条弦,OE,OF为AB、CD的弦心距。你能添加什么条件,使得∠AOB=∠COD?
BAOECDF∵ OE = OF, OE,OF为AB、CD的弦心距(已知)
∴ ∠AOB=∠COD(同圆中,如果弦心距相等,
那么所对的圆心角相等)∵ AB = CD(已知)
∴ ∠AOB=∠COD(同圆中,如果弦相等,
那么所对的圆心角相等)
∵ AB = CD(已知)
∴ ∠AOB=∠COD(同圆中,如果弧相等,
那么所对的圆心角相等)⌒⌒抢答解 ∵OC=OD( ),
∴ ( )。 ∵ (已知)
∴∠D=∠3( ),
∠C=∠1( )。∵∠2=∠1( ),
∴∠2=∠1=∠BOD(等量代换)。⌒⌒⌒同圆的半径相等等边对等角CD∥AB两直线平行,内错角相等两直线平行,内错角相等对顶角相等∠C=∠D 同圆中,如果圆心角相等 ,那么所对的劣弧(或优弧)相等思考与提高 折折剪剪:你能利用今天所学的知识将一个圆面用剪刀剪成一个边长相等的八边形吗?思考:在同圆中,如果圆心角扩大2倍,那么所对的弧,所对的弦怎样变化呢?
ABCO12小结
1.这节课学习了哪些具体内容?
(1)弦、弦心距、半圆、优弧、劣弧、等圆的概念
(2)圆的性质:在同圆或等圆中,如果两个圆心角、
两条劣弧(或优弧)、两条弦或两条弦的弦心距,
这四组量中有一组量相等,那么它们所对应的其
余三组量也分别相等。下课啦!谢谢各位老师的光临!作业:1. 课本第80页练习1和3
2. A册习题16.2
一、教材分析 在学习本节课前,学生已经掌握了圆的一些基本知识和旋转的有关概念。这节课有关圆的性质是今后进一步学习圆的必不可少的基础。二、教学目标 1.理解弦、弦心距、半圆、优弧、劣弧、等圆的概念;
2.掌握在同圆或等圆中,圆心角、弧、 弦、弦心距之
间的关系,并初步学会运用这些关系解决有关问题;
3.通过操作和多媒体演示,培养学生观察、分析、归
纳的能力,向学生渗透旋转变换的思想及由特殊到一
般的认识规律 。 三、教学重点和难点 重点:在同圆或等圆中,圆心角、弧、弦、
弦心距之间的关系;
难点:推出在同圆或等圆中圆心角、弧
弦、弦心距之间的关系。
四、教学准备 用硬纸板做两个圆,大头针,尺,多媒体课件,电脑五、教学过程设计 (一)、创设情景,引入新课
1、复习旧知:圆的半径、直径、周长公式、面积公式等知识。
2.操作:让⊙O绕圆心旋转任意角度,观察发现什么结论。
结论:圆不论绕圆心旋转多少度,都能够和原来的图形重合。(用flash)
3、用旋转的角度复习圆心角概念(半径绕圆心旋转),引出弧(半圆、优弧、劣弧)(动点A绕圆心旋转)、弦、弦心距的概念。(用几何画板,这是对有关概念的动态认识)
把圆心角,弧、弦、弦心距的概念和圆的旋转联系起来。使概念形象化,孕伏了“轨迹”的思想。
这节课我们就来研究在同圆或等圆中圆心角及所对的弧、弦、弦的弦心距之间的关系(引出课题)
(二)、大胆猜想,发现性质 1、在⊙O中,再画圆心角∠A′OB′,使∠AOB=∠A′OB′
再作出它们所对的弦AB,A′B′和弦的弦心距OM,OM′
猜想,其余三组量∠AOB=∠A′OB′所对的弧、弦、弦心
距的大小关系如何?为什么?(用几何画板,教师边演示,边
启发学生得出结论)
简单的猜想和多媒体演示得出圆的性质,使学生产
生学习的兴趣和自信心。直观,易懂,激发学生积
极思考。
2、在等圆中呢?(用两圆叠合)
3、圆的性质:在同圆或等圆中,如果圆心角相等,那么所对的劣弧(或优弧)相等,所对的弦相等,所对的弦的弦心距相等。
性质的条件和结论分别是什么?并用符号语言表示。
在教学中,重点突破第一条性质。通过第一条性质的突破,使学生提高观察分析、归纳能力。以学生为主体,从而突破本节课的难点。
4、思考,在同圆或等圆中,把圆心角相等与三个结论中的任何一个交换位置,可以得到三个新的结论,这三个结论正确吗?简单说明为什么。判断题(1)因为∠AOB= ∠A’OB’,
所以AB=A’B’
(2)在⊙O和⊙O’中,OC和OC’是AB和A’B’的弦心距
如果∠AOB= ∠A’OB’,
那么OC=O’C’(╳)(╳)(三)、巩固应用、变式练习强调前提在同圆或等圆中.提问中差学生,调动学习积极性,培养学习兴趣,增强自信心。例1 如图,⊙O中,AB=CD,OE、OF分别是AB、CD的弦心距。(2)OE和OF相等吗?为什么?⌒⌒(四)、例题精选DBCoAEF这题以口答形式,使学生对新知灵活应用,利用所学知识进行简单说理。(1)∠B与∠C相等吗?为什么?(2) OD和OE是AB、BC的弦心距,若OD=OE,请问△ABC是什么三角形?∠A、∠B、∠C为多少度?为什么?⌒⌒oEDCBA这题让学生书写 。
巩固并熟悉新知,并能简单说理。 抢答题
AB,CD是⊙O的两条弦,OE,OF为AB、CD的弦心距。你能添加什么条件,使得∠AOB=∠COD?
通过开放性提问,熟悉圆的性质中条件和结论的准确应用。(1)∵ (已知)
∴∠AOB=∠COD(同圆中,如果弧相等,那么所对的圆
心角相等)
(2)∵ AB=CD(已知)
∴∠AOB=∠COD(同圆中,如果弦相等,那么所对的圆
心角相等)
(3)∵OE=OF, OE,OF为AB、CD的弦心距(已知)
∴ ∠AOB=∠COD(同圆中,如果弦心距相等,那么所
对的圆心角相等)⌒⌒⌒这题用填空形式。能应用圆的性质简单说理 。五、思考与提高 折折剪剪:你能利用今天所学的知识将一个圆面用剪刀剪成一个边长相等的八边形吗?八等分后折成的扇形用剪刀把它剪成三角形,则展开后是什么图形?为什么?
通过生活中的实际问题,让学生操作,激发学生学习数学的积极性,对所学知识巩固、提高。
2、思考:在同圆中,如果圆心角扩大2倍,那么所对的弧,所对的弦怎样变化呢?
ABCO12
(六)师生共同小结
(1)弦、弦心距、半圆、优弧、劣弧、等圆的概念
(2)在同圆或等圆中,如果两个圆心角、两条劣弧(或优
弧)、两条弦或两条弦的弦心距,这四组量中有一组
量相等,那么它们所对应的其余三组量也分别相等。
(3)注意前提条件 “在同圆或等圆中”
(七)布置作业
1. 课本第80页练习1和3
2. A册习题16.2 六、教学说明教学形式:多媒体辅助教学
教材结构设计:引入问题—探索分析—归纳—结论—应用
