函数[下学期]

第三单元 函数
第11课 函数的基本概念（含直角坐标系）
1．函数是研究( )
A．常量之间的对应关系的 B．常量与变量之间的对应关系的
C．变量与常量之间对应关系的 Ｄ．变量之间的对应关系的
2.点M（-3，-5）向上平移7个单位到点M1的坐标为( )
A.(-3,2) B.(-2,-12) C.(4,-5 ) D.(-10,-5)
3.点M在y轴的左侧，到x轴、y轴的距离分别是3和5，则点M的坐标是（　　）
A.(-5,3) B .(-5，-3)
C．(5，3)或（-5，3） D.-5，3)或（-5，-3）
4．△DEF是由△ABC平移得到的，点A（－1，－4）的对应点为D（1，－1），则点B（1，1）的对应点E、点C（－1，4）的对应点F的坐标分别为（ ）
A．（2，2），（3，4） B．（3，4），(1，7)
C．（－2，2），（1，7） D．（3，4），（2，－2）
5．已知M（1,-2），N(-3,-2)则直线MN与x轴，y轴的位置关系分别为（　　）
A.相交，相交 B.平行，平行
C.垂直相交，平行 D.平行，垂直相交
6．点A（m，n）满足0，则点A在（ ）上
A．原点 B．坐标轴 C．x轴 D．y轴
7．在匀速运动公式中,表示速度,表示时间,表示在时间内所走的路程,则变量是________,常量是_______.
8．函数中自变量x的取值范围是___________.
9．拖拉机开始工作时，油箱中有油40升，如果每小时耗油5升，如图是拖拉机工作时，油箱中的余油量Q（升）与工作时间 （小时）的函数关系图像,那么图中 应是______.
10．王华和线强同学在合作电学实验时，记录下电流I（安培）与电阻R（欧）有如下对应关系.观察下表：
R …… 2 4 8 10 16 ……
I …… 16 8 4 3.2 2 ……
你认为I与R间的函数关系式为________；当电阻R＝5欧时，电流I＝____安培.
11．在某公用电话亭打电话时，需付电话费y（元）与通话时间 x（分钟）之间的函数关系用图象表示如图.小明打了2分钟需付费______元；小莉打了8分钟需付费_______元.
(第9题图) (第11题图)
12．线段AB中，点A（-2，3）, 点B（1，3），现把线段AB平移到A’B’，使A’（0，2），B’（3，2），则直线AB、A’B’间的距离为
13．以0为原点,正东、正北方向为x轴、y轴正方向建立平面直角坐标系,一个机器人从原点O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2,再向正西方向走9米到达A3,再向正南方向走12米到达A4,再向正东方向走15米到达A5,按此规律走下去，当机器人走到A6时, A6的坐标是_____________
14．在某城市中，体育场在火车站以西4000m再往北2000m处，华侨宾馆在火车站以西3000m再往南2000m处，百佳超市在火车站以南3000m再往东2000m处，请建立适当的平面直角坐标系，分别写出各地的坐标。
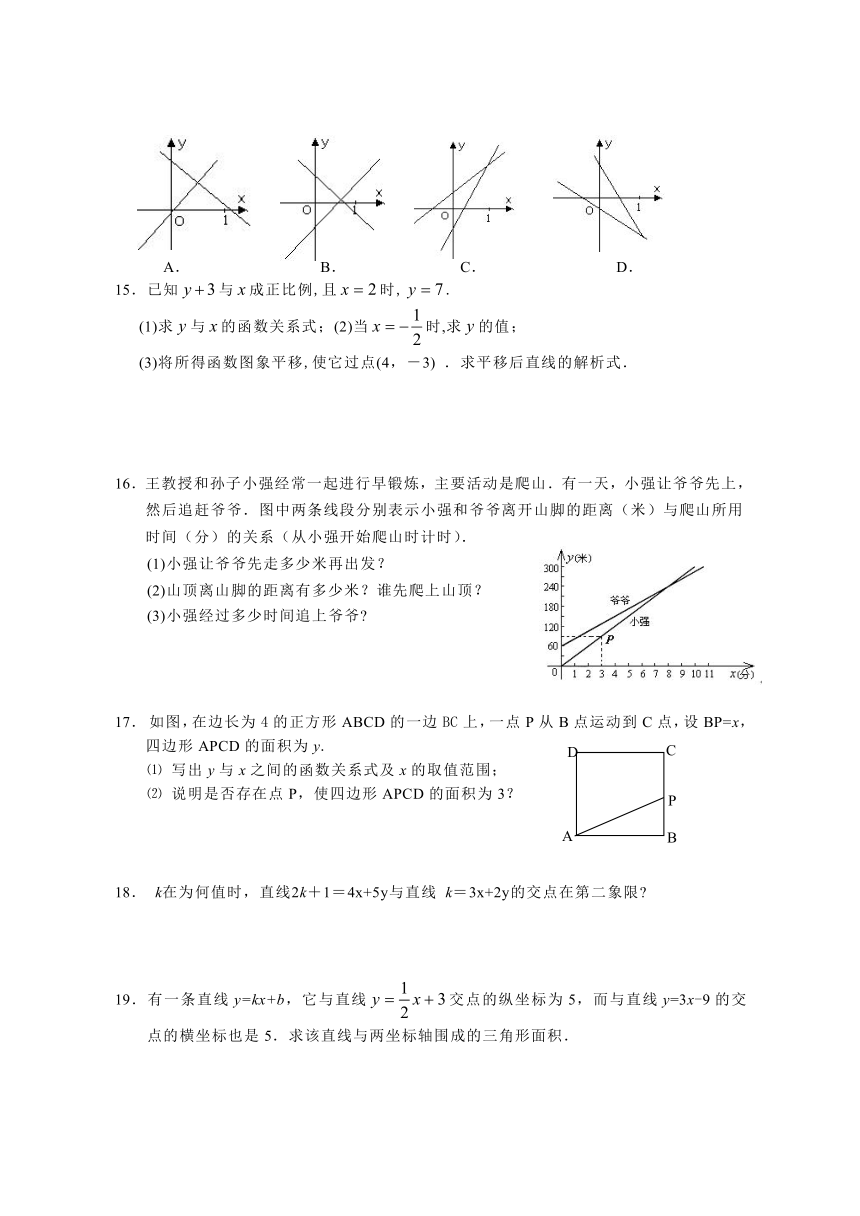
15．一天上午8时，小华去县城购物，到下午14时返回家，结合图象回答：
(1)小华何时第一次休息？
(2)小华离家最远的距离时多少？
(3)返回时平均速度是多少？
(4)请你描述一下小华购物的情况.
第12课 一次函数
1．一次函数的图象经过点（－2，3）与（1 ，－1），它的解析式是___ _____．
2．将直线y＝3x向上平移5个单位，得到直线 ；将直线y＝-x-5向下平移5个单位，得到直线 .
3．平行四边形相邻的两边长为x、y，周长是50，则y与x的函数关系式是__________．
4．出租车收费按路程计算，3km内（包括3km）收费10元；超过3km每增加1km加收１元，则路程x≥3km时，车费y（元）与x (km)之间的函数关系式是________________．
5．已知点P（3a +1，a + 3）是第二象限内坐标为整数的点，则整数a的值是_______．
6．若直线和直线的交点坐标为(),则____________．
7．下列函数中，与y＝x表示同一个函数的是 （ ）
Ａ．y＝ Ｂ． Ｃ．y＝()2 Ｄ．y＝
8．下列关系式中，不是函数关系的是 （ ）
Ａ．y=(x<0) Ｂ．y=±(x>0) Ｃ．y=(x>0) Ｄ．y=－(x>0)
9．若m＜0, n＞0, 则一次函数y=mx+n的图象不经过 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
10．已知函数y＝2x+1，当自变量增加m时，相应的函数值增加 （ ）
Ａ．2 m+1 Ｂ．2 m Ｃ．m Ｄ．2m－1
11．汽车由Ａ地驶往相距360km的B地，它的平均速度是60km/h，则汽车距Ｂ地路程s(km)与行驶时间t(h)的函数关系式及自变量t的取值范围是（ ）
Ａ．S=360－60t (0≤t≤6) Ｂ．S=360－60t (t>0)
Ｃ．S=60t (0≤t≤6) Ｄ．S=60t (t<6)
12．已知函数，当时，y的取值范围是 （ ）
A． B． C． D．
13．小平的父亲散步，从家中走20分钟到一个离家900米的报亭看10分钟的报纸后，用15分钟返回家中，下列图形中表示小平父亲离家的时间与距离之间的关系是（ ）
A． B． C． D．
14．当时，函数y=ax+b与在同一坐标系中的图象大致是（ ）
A． B． C． D．
15．已知与成正比例,且时,.
(1)求与的函数关系式；(2)当时,求的值；
(3)将所得函数图象平移,使它过点(4，－3) ．求平移后直线的解析式．
16．王教授和孙子小强经常一起进行早锻炼，主要活动是爬山．有一天，小强让爷爷先上，然后追赶爷爷．图中两条线段分别表示小强和爷爷离开山脚的距离（米）与爬山所用时间（分）的关系（从小强开始爬山时计时）．
(1)小强让爷爷先走多少米再出发？
(2)山顶离山脚的距离有多少米？谁先爬上山顶？
(3)小强经过多少时间追上爷爷
17． 如图，在边长为4的正方形ABCD的一边BC上，一点P从B点运动到C点，设BP=x，四边形APCD的面积为y.
⑴ 写出y与x之间的函数关系式及x的取值范围；
⑵ 说明是否存在点P，使四边形APCD的面积为3？
18． k在为何值时，直线2k＋1＝4x+5y与直线 k＝3x+2y的交点在第二象限
19．有一条直线y=kx+b，它与直线交点的纵坐标为5，而与直线y=3x-9的交点的横坐标也是5．求该直线与两坐标轴围成的三角形面积．
第13课 反比例函数
1．若反比例函数y=的图像经过点A(－2，3) ，那么m= ．
2．△ABC的面积为6，BC边的长度为x，BC边上的高为y，则y与x之间的函数关系式为 ．
3．如图所示，点A在反比例函数y=图像上，
且AB⊥x轴，垂足为B，若S△AOB=6，
则k= ．
4．若y－3与x+5成反比例，且x=3时y=5，那么当y=7时，x= ．
5．已知反比例函数y=(2k-5)xk2-10的图像在所在像限内，y随x的增大而减小，则k= ．
6．反比例函数y=（x>0）在平面直角坐标系中，绕着坐标原点O逆时针旋转90°后，所得到的图像解析式是（注明自变量的取值范围） ．
7．如图所示，A、C是函数y=图像上任意两点，
过A作x轴垂线，垂足为B，过C点作y轴的垂线，
垂足为D，且Rt△AOB，Rt△OCD的面积分别记为
S1和S2，则S1　　　　　S2 (比较大小关系)
8．下面哪个点在反比例函数y=的图像上（ ）．
A．（3，1） B．（-3，1） C．（3，） D．（，3）
9．已知一次函数y=-x+4与反比例函数y=在同一平面直角坐标系内的图像没有交点，则k的取值范围是（ ）
A．k > 0 B．k < 0 C．k > - 4 D．k > 4
10．直线y=x+4与双曲线y=的交点为A、B，O为坐标原点，求△AOB面积．
11．如图所示，在平面直角坐标系中，射线OM与反比
例函数的图像相交于点A，且∠MOx=45°，OA=3，
求：（1）点A的坐标；
（2）此反比例函数的解析式．
12．已知反比例函数y=和一次函数y=ax+b的图像的一个交点A的坐标为（-3，4）且一次函数的图像与x轴的交点到原点的距离为5，求反比例函数和一次函数的解析式．
13．已知：y=y1 – y2 ，y1与x成正比例，y2与x2成反比例，且当x=1时y= －2；x= －1时y=－6，求y与x之间的函数关系式．
14．设x1、x2是关于x的一元二次方程kx2+2(k－3)x+k－3 = 0的两个不相等实数根（k为非负整数），一次函数y=(k －2)x+m与反比例函数y =的图像都经过点（x1，x2），
试求：（1）k的值；
（2）一次函数与反比例函数的解析式．
15．已知反比例函数y=(k<0)的图像经过点A（－，m），过点A作AB⊥x轴于点B，且S△AOB =．
（1）求k和m的值；
（2）若一次函数y=ax+1的图像经过点A，并且与x轴相交于
点C,求∠ACO的度数和∣AO∣：∣AC∣的值．
第14课 二次函数
1．抛物线y=x2+5x- 6与x轴的交点坐标为 ，与y轴的交点坐标为 ．
2．若抛物线y=(m - 1)xm2- m的开口向上，则m的值为 ．
3．将二次函数y =3x2+6x+12 化为y=a(x- h)2+k 的形式则y= ．顶点坐标 ，对称轴 ，当x 时函数值y随x的增大而减小．
4．抛物线y=ax2+bx+c与抛物线y=x2- 3x-4关于x轴对称，则abc = ．
5．抛物线y =2x2 – 3x – 1的图像在x轴上截得的线段的长为 ．
6．抛物线y=ax2+bx+c与x轴有两个交点，一个交点为（2，0），对称轴直线x = 4，则另个一交点坐标为 ．
7．已知二次函数y = ax2-bx+c的图像如图所示，
则点P（a, ）在 （ ）
A．第一像限 B．第二像限
C．第三像限 D．第四像限
8．在同一直角坐标系中，如图所示直线y= ax+b和抛物线y= ax2+bx的图像只可能是（ ）
9．二次函数y = x2的图像向上平移2个单位再向右平移3个单位，得到新图像的二次函数解析式为（ ）
A．y = (x+2)2 – 3 B．y =(x+2)2 + 3
C．y = (x - 2)2+3 D．y=(x-2)2 – 3
10．下列哪两条抛物线关于x轴对称（ ）
A．y =－x2 +2x +5 与 y =－x2+2x－5 B．y = －x2 +2x +5 与 y =-x2 － 2x +5
C．y =－x2 +2x +5 与 y =－x2 －2x－5 D．y = －x2 +2x +5 与 y =x2 －2x －5
11．已知抛物线和直线L在同一直角坐标系中的图像如图所示，
抛物线的对称轴为直线x = －1 ，P1(x1 , y1 )、P2(x2 , y2 )是抛物
线上的点，P3(x3, y3 )是直线L上的点，且 －1则y1、y2、y3的大小关系是（ ）
A．y1C．y312．二次函数y=ax2+bx+c的图像如图所示，则下列 y
不等式成立的个数是（ ）
①abc <0 ② a+b+c <0 ③a+c > b ④ a <
A．1 B．2 C．3 D．4 -1 o 1 x
13．根据下列条件求二次函数的解析式；
（1）二次函数图像经过点（0，3）、（－2 ，－5）、（1，4）； （第12题图）
（2）二次函数图像经过点（4，1），且顶点为（3，－1）；
（3）二次函数图像经过点（0，0）、（12，0），且顶点到x轴的距离为3；
14．已知二次函数y = ax2+bx-5的图像的对称轴为直线x=3，图像与y轴交于点B，设x1、
x2是方程ax2+bx – 5 = 0的两根，且x12 +x22 =26，求：
（1）二次函数的解析式和顶点A的坐标；
（2）原点O到直线AB的距离．
15．已知抛物线y = ax2+bx+c（a≠0）与x轴交于不同的两点A和B（4，0），与y轴交于点C（0，8），其对称轴为x =1；
（1）求此抛物线的解析式；
（2）过A、B、C三点作⊙O′与y轴的负半轴交于点D，求经过原点O且与直线AD垂直（垂足为E）的直线OE的方程．
第15课 函数的应用(1)
1．如右图，是某生物实验室的温度自动描点记录仪所录绘该室2004年4月8日的气温随时间变化的图象. 请你结合下表观察图象记录中的7个点，大致估计表中缺失的数据并补写出来：________.
　
2．南通市与庄河两地之间的距离是160千米，若汽车以平均每小时80千米的速度从南通开往庄河，则汽车距庄河的路程s（千米）与行驶的速度t（小时）之间的函数关系式为_________________．
3．我们学习过反比例函数． 例如，当矩形面积S一定时，长a是宽b的反比例函数，其函数关系式可以写为（S为常数，S≠0）．
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例，并写出它的函数关系式．
实例：_________________________________________________；
函数关系式：___________________________________________．
4．点在双曲线上，则k=______________．
5．已知抛物线与x轴有两个交点，那么一元二次方程的根的情况是______________________．
6．已知二次函数的图象开口向上，且与y轴的正半轴相交，请你写出一个满足条件的二次函数的解析式：_____________________．
7．某闭合电路中，电源的电压为定值，电流I（A）与电阻R（Ω）成反比例．右图表示的是该电路中电流I与电阻R之间的图象，则用电阻R表示电流I的函数解析式为（ ）
A． B．
C． D．
8．抛物线的对称轴是直线（ ）
A． B． C． D．
9．强在劳动技术课中要制作一个周长为80cm的等腰三角形，请你写出底边长y（cm）与一腰长x（cm）的函数关系式，并求出自变量x的取值范围．
10．某农民带了若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售， 售出土豆千克数与他手持有的钱数（含备用零钱）的关系如右图所示，结合图象回答下列问题：
（1）农民自带的零钱是多少？
（2）降价前他每千克土豆出售的价格是多少？
（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？
11．环岛高速公路上，一辆轿车和一辆货车沿相同路线从A地到B地，所经过的路程y（千米）与时间x（小时）的函数关系如图所示，试根据图象回答下列问题：
（1）货车比轿车早出发__________小时，轿车追上货车时行驶了__________千米，A地到B地的距离为_________千米．
（2）轿车追上货车需要多小时？
（3）轿车比货车早到多少时间？
.
第16课 函数的应用(2)
1．在平面直角坐标系中，直线（k，b为常数k≠0，b>0）可以看成是将直线　沿y轴向上平行移动b个单位得到的，那么将直线沿x轴向右平行移动m个单位（m>0得到的直线方程是____________．
2．若一次函数的图象经过第一、二、四象限，则m的取值范围是________．
3．近视眼镜的度数y（度）与镜片焦距x（米）成反比例． 已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数y与镜片焦距x之间的函数关系式是____________．
4．有一个二次函数的图象，三位同学分别说出它的一些特点：
甲：对称轴是直线；
乙：与x轴两个交点的横坐标都是整数；
丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3．
请你写出满足上述全部特点的一个二次函数解析式：　　　　　　　　　　　　　　　
5．两条直线与在同一坐标系中的图象可能是下图中的（ ）


6．如果反比例函数的图象经过点，那么下列各点在此函数图象上的是（ ）
A． B． C． D．
7．南通市某中学环保兴趣小组对南胡清除淤泥工程进行调查，并从《南通晚报》上收集到下列数据：
南胡面积（单位：米2） 淤泥平均厚度（单位：米） 每天清淤泥量（米3）
160万 0.7 0.6万
根据上表解答下列问题：
（1）请你按体积=面积×高来估算，南胡的淤泥量大约有多少万立方米？
（2）设清除淤泥x天后，剩余的淤泥量为y（万米3），求y与x的函数关系（不要求写出自变量x的取值范围）．
（3）为了使南胡的生物链不遭到破坏，仍需保留一定量的淤泥. 若需保留的淤泥量约为22万米3，求清除淤泥所需天数．
8．某地举办乒乓球比赛的费用y（元）包括两部分：一部分是租用比赛场地等固定不变的费用b（元），另一部分与参加比赛的人数x（人）成正比例. 当x=20时，y=1600；
当x=30时，y=2000．
（1）求y与x之间的函数关系式；
（2）如果有50名运动员参加比赛，且全部费用由运动员分摊，那么没2名运动员需要支付多少元？
9．在压力不变的情况下，某物承受的压强P（Pa）是它的受力面积S（m2）的反比例函数，其图象如右图所示：
（1）求P与S之间的函数关系式；
（2）求当S=0.5m2时物体所受的压强P．
10．卢浦大桥拱形可以近似地看作抛物线的一部分，在大桥截面1:11000的比例图上去，跨度AB=5cm，拱高OC=0.9cm，线段DE表示大桥拱内桥长，DE∥AB，如图（1）， 在比例图上，以直线AB为x轴，抛物线的对称轴为y轴，以1cm作为数轴的单位长度，建立平面直角坐标系，如图（2），
（1）求出图（2）上以这一部分抛物线为图象的函数解析式，写出函数定义域；
（2）如果DE与AB的距离OM=0.45cm，求卢浦大桥拱内实际桥长（备用数据：≈1.4，计算结果精确到1米）．


第三单元 函数检测卷
（总分100分，时间60分钟）
一．填空题（本题共6小题，每小题3分，共18分．）
1．如果反比例函数的图象位于第二、第四象限内，那么满足条件的正整数k可能的值是 ．
2．若一次函数y=ax+1―a中，y随x的增大而增大，且它的图像与y轴交于正半轴，则
|a―1|+= ．
3．请写出一个开口向上，与y轴交点纵坐标为-1，且经过点(1，3)的抛物线的解析式 ．
4．一次函数的图象经过点P和Q，则 的值为____________．
5．矩形AOCB的两边OC、OA分别位于轴、轴上，点B的坐标为B（），D是AB边上的一点.将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图像上，那么该函数的解析式是_______．
6．如图，△P1OA1、△P2OA2是等腰直角三角形,点、在函数的图象上，斜边、都在轴上,则点的坐标是________________．
二．选择题（每题3分，共33分）
7．若代数式在实数范围内有意义，则x的取值范围为( )
A．x>0 B．x≥0 C．x≠0 D．x≥0且x≠1
8．反比例函数的图象位于（ ）
A．第一、三象限 B．第二、四象限 C．第一、四象限 D．第二、三象限
9．如图，一次函数的图像经过A、B两点，则解集是 （ ）
A． B． C． D．
10．抛物线y=3(x-1)+1的顶点坐标是（ ）
A．（1，1） B．（-1，1） C．（-1，-1） D．（1，-1）
11．直线与轴、轴所围成的三角形的面积为（ ）
A．3 B．6 C． D．
12．小亮早晨从家骑车到学校，先上坡后下坡，行程情况如图所示．若
返回时上坡、下坡的速度仍保持不变，那么小明从学校骑车回家 用的时间是（ ）
A．37.2分钟 B．48分钟 C．30分钟 D．33分钟
13．已知y是x的一次函数，下表中列出了部分对应值，则m等于（ ）
x －1 0 1
y 1 m －1
A．－1 B．0 C． D．2
14．下列四个函数中，y随x增大而减小的是( )
A．y=2x B．y=―2x+5 C．y=― D．y=―x2+2x―1
15． 在同一平面直角坐标系中，一次函数和二次函数的图象可能为（ ）
16．根据下列表格中二次函数的自变量与函数值的对应值，判断方程（为常数）的一个解的范围是（　　）　
6.17 6.18 6.19 6.20
A． B．
C． D．
三．解答题
17.( 6分)如图，直线经过点A（－3，1）、B（0，－ 2），将该直线向右平移2个单位得 到直．
（1）在图（7）中画出直线的图象；
（2）求直线的解析式．
18． (7分)已知函数
（1） 求函数的最小值；
（2） 在给定坐标系中，画出函数的图象；
（3） 设函数图象与x轴的交点为A（x1，0）、B（x2，0），求的值．
19． (8分)如图，一次函数的图象与反比例函数图象交于A（－2，1）、B（1，n）两点．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．
20． (8分) 为了鼓励市民节约用水，自来水公司特制定了新的用水收费标准，每用水量，x(吨)与应付水费(元)的函数关系如图．
(1)求出当月用水量不超过5吨时，y与x之间的函数关系式；
(2)某居民某月用水量为8吨，求应付的水费是多少
21． (10分)某企业信息部进行市场调研发现：
信息一：如果单独投资A种产品，则所获利润yA(万元)与投资金额x(万元)之间存在正比例函数关系：yA=kx，并且当投资5万元时，可获利润2万元；
信息二：如果单独投资B种产品，则所获利润yB(万元)与投资金额x(万元)之间存在二次函数关系：yB=ax2＋bx，并且当投资2万元时，可获利润2.4万元；当投资4万元，可获利润3.2万元．
(1)请分别求出上述的正比例函数表达式与二次函数表达式；
(2)如果企业同时对A、B两种产品共投资10万元，请你设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少．
22．(10分)某校的围墙上端由一段段相同的凹曲拱形栅栏组成，如图所示，其拱形图形为抛物线的一部分，栅栏的跨径AB间，按相同的间距0.2米用5根立柱加固，拱高OC为0.6米．
（1） 以O为原点，OC所在的直线为y轴建立平面直角坐标系，请根据以上的数据，求出抛物线
y=ax2的解析式；
（2）计算一段栅栏所需立柱的总长度．（精确到0.1米）
数与代数综合测试（一）
（时间100分　满分100分）
一．填空题：（每小题2分，共20分）
1.用代数式表示：a的相反数的平方与b的绝对值的和是__________．
2.用科学计数法表示：(1)－0.0000015=_________；(2)125000000=___________．　　　
3.计算：=_________．
4.分解因式：=__________________．
5.已知函数，当x=1时，y=_________．
6.把抛物线向左平移2个单位，再向下平移1个单位，得到的解析式是_______．
7.不等式3x－4≥4＋2（x－2）的最小整数解是__________．
8.函数y=的自变量x的取值范围是___________．
9.当a____________时，关于x的方程（a－2）x2+（－2a+1）x+a=0有两实数根．
10.样本2，4，1，2，1的平均数为_____，方差为_____．
二.选择题：（每小题2分，共20分）
11.下列各式中，一定正确的是 （ ）
A.x+2x=x2 B.x2÷x=x C. (1+x)2=1+x2 D. (xy)2=xy2.
12.二次函数y=ax2+bx+c中，b2=4ac且x=0时y=-4,则 （ ）
A.y最大值=-4 B.y最小值=-4 C. y最大值=-3　 D. y最小值=-3　
13.下列说法正确的是 （ ）
A.负数和零没有平方根　　 B. -2002的倒数是2002
C.0.5是分数　　　　　　　 D.0和1的相反数是它本身
14.设(x＋y)(x＋2＋y)－15＝0，则x＋y的值是 　　　　（ ）
　　A.－5或3　 B.-3或5　 C.3 　 D.5
15.二次函数y＝x＋x＋a－2的图象与x轴只有一个交点，则a的值为（ ）
A.2 B.－2 C. D.4
16.在同一直角坐标系中，函数y=3x与y=图象大致是 （ ）
17.如果分式的值为零，那么x等于（　　　）
A.－1　　B.1　　C.－2或1　　D.1或2
18.某餐厅共有7名员工，所有员工的工资情况如下所示：
人员 经理 厨师 会计 服务员
人数 1 2 1 3
工资数 2800 600 520 340
则餐厅所有员工工资的众数、中位数是　　（　　　）
A.340　　520　　 B.520　　340
C.340　　560　　 D.560　　34020
19．生物学指出：生态系统中，每输入一个营养级的能量，大约只有10%的能量能够流动到下一个营养级，在M1→M2→M3→M4→M5→M6 这条生物链中（Mn表示第n个营养级，n=1,2,...,6）,要使M6获得10千焦的能量，那么需要M1提供的能量约为（　　）
A.104千焦　　　B.105千焦　　　C.106千焦　　　D.107千焦　
20.下列函数中，自变量x的取值范围为x≤1的是 　　　（ ）
　 A.y=x-1 B.y= C.y= D.y=
三．计算题：（每小题4分，共16分）
21.（–1）-1 +－（－）0 －3·tan300
22.
23.()-1-sin300-()0
24.化简求值：.其中a=+1,b=-1
四.解方程：（6分）
25.
五.（本题6分）
26.解不等式组：
　　　　
　　　　
六.（每小题10分，共20分）
27.已知一次函数y＝kx＋b图象不经过第四象限，而过点(1,3)，又知系数k是方程3x2 －5x－2＝0的一个根，求这一次函数的解析式.
　
28.若二次函数y＝ax2 ＋bx＋c中，c＝3，图象的顶点坐标为(2,-1)，求二次函数的解析式．
七.（本题12分）
x 3 5 9 11
y 18 14 6 2
29 .某商场经营一批进价为2元一件的小商品，在市场营销中发现下商品的日销售单价x元与日销售量y件之间有如下关系：
(1)在所给的直角坐标系①中
①根据表中提供的数据描出实数对(x, y)的对应点；
②猜测并确定日销售量y件与日销售单价x元之间的函数关系式，并画出图像。
(2)设经营此商品的日销售利润(不考虑其他因素)为P元，根据日销售规律：
①试求日销售利润P元与日销售单价x元之间的函数关系式，并求出日销售单价x为多少时，才能获得最大日销售利润。试问日销售利润P是否存在最小值？若有，试求出，若无，请说明理由。
②在给定的直角坐标系(图2)中，画出日销售利润P元与日销售单价x元之间的函数图像的简图。观察图像，写出x与P的取值范围。
数与代数综合检测（二）
（总分100分，时间60分钟）
一．填空题（每题2分，共20分）
1．计算 2 一的结果是（ ）
A . 1 B. －1 C ．一 7 D ． 5
2．近几年安徽省教育事业加快发展，据 2005 年末统计的数据显示，仅普通初中在校生就约有334 万人，334 万人用科学记数法表示为（　　　　）
A ． 3 . 34 106人 B ． 33 .4 10 5人
C．334 104 人 D ． 0 . 334 107 人
3．计算（-ab）的结果正确的是（　　　　）
A． B． C．- D．-
４．方程的根是（　　　　　　）
A．－3 B．0 C．2 D．3
5．数据7、9、8、10、6、10、8、9、7、10的众数是（　　）
A．7 B．8 C．9 D．10
6．在一个暗箱里,装有3个红球、5个黄璋和7个绿球，它们除颜色外都相同,搅拌均匀后，从中任意摸出一个球是红球的概率是( )
A. B. C. D.
7．有两块面积相同的小麦试验田，分别收获小麦9000kg和15000kg．已知第一块试验田每公顷的产量比第二块少3000kg，若设第一块试验田每公顷的产量为xkg，根据题意，可得方程（　　）
A．　　B．　　C． D．
8．如果两点P1(1，y1)和P2(2，y2)在反比例函数的图象上，那么（　　　　）
A．y2＜y1＜0 B．y1＜y2＜0 C．y2＞y1＞0 D．y1＞y2＞0
9． Rt△ABC中，斜边AB=4，∠B=60 ，将△ABC绕点B旋转60 ，顶点C运动的路线长是
A． B． C． D．
10．已知函数y＝x－5，令x＝、1、、2、、3、、4、、5，可得函数图象上的十个点．在这十个点中随机取两个点P（x1，y1）、Q（x2，y2），则P、Q两点在同一反比例函数图象上的概率是（　　）
A． B． C． D．
三、解答题（每题2分，共12分）
11．当x＝＿＿＿＿时，分式没有意义．
12．如图是地球表面积统计图的一部分，扇形A表示地球陆地面积，则此扇形的圆心角为＿＿＿度．
13．化简(＋)÷的结果是＿＿＿．
14．如图，∠C＝∠E＝90°，AC＝3，BC＝4，AE＝2，则AD＝＿＿＿．
15．如图，矩形纸片ABCD，AB＝2，∠ADB＝30°，沿对角线BD折叠使△ABD和△EBD落在同一平面内，则A、E两点间的距离为＿＿．
16．定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n＋5；②当n为偶数时，结果为（其中k是使为奇数的正整数），并且运算重复进行．
例如，取n＝26，则：
若n＝449，则第449次“F运算”的结果是＿＿＿＿＿．
三、解答题
17.(本题8分)
(1)计算：. （2）解方程： .
18． 已知一次函数y=x+m与反比例函数的图象在第一象限的交点为P(x0，2).
(1) 求x0及m的值；
(2) 求一次函数的图象与两坐标轴的交点坐标.
19．　　　　　　
根据对话的内容，试求出饼干和牛奶的标价各是多少元？
20．某区从2300名参加初中毕业升学统一考试数学试测的学生
中随机抽取200名学生的试卷，成绩从低到高按59～89、90
～119、120～134、135～150分成四组进行统计（最低成绩
为59分，且分数均为整数），整理后绘出如图所示的各分数
段频数分布直方图的一部分．已知前三个小组从左到右的频
率依次为0．25、0．30、0．35．
⑴第四组的频数为　　　　　　，并将频数分布直方图 补充完整；
⑵若90分及其以上成绩为及格，则此次测试中数学成绩及格以上（含及格）的人数约为　　　　　　　　．
21． 某乒乓球训练馆准备购买n副某种品牌的乒乓球拍，每副球拍配k(k≥3)个乒乓球. 已知A、B两家超市都有这个品牌的乒乓球拍和乒乓球出售，且每副球拍的标价都为20元，每个乒乓球的标价都为1元 . 现两家超市正在促销，A超市所有商品均打九折(按原价的90%付费)销售，而B超市买1副乒乓球拍送3个乒乓球 . 若仅考虑购买球拍和乒乓球的费用，请解答下列问题：
(1) 如果只在某一家超市购买所需球拍和乒乓球，那么去A超市还是B超市买更合算？
(2) 当k=12时，请设计最省钱的购买方案.
22.（12分)．近期，海峡两岸关系的气氛大为改善．大陆相关部门于2006年9月1日起对原产台湾地区的15种水果实施进口零关税措施，扩大了台湾水果在大陆的销售．某经销商销售了台湾水果凤梨，根据以往销售经验，每天的售价与销售量之间有如下关系：
每千克售价（元） 38 37 36 35 … 20
每天销量（千克） 50 52 54 56 … 86
设当单价从38元/千克下调了元时，销售量为千克；
（1）写出与间的函数关系式；
（2）如果凤梨的进价是20元/千克，某天的销售价定为30元/千克，问这天的销售利润是多少？
（3）目前两岸还未直接通航，运输要绕行，需耗时一周（七天），凤梨最长的保存期为一个月（30天），若每天售价不低于30元/千克，问一次进货最多只能是多少千克？
23．（ 12分)．如图，在平面直角坐标系中，点A、B分别在x轴、y轴上，线段OA、OB的长(0A(1)求点C的坐标；
(2)求直线AD的解析式；
(3)P是直线AD上的点，在平面内是否存在点Q，使以0、A、P、Q为顶点的四边形是菱形 若存在，请直接写出点Q的坐标；若不存在，请说明理由．
第三单元 函数
第11课 函数的基本概念（含直角坐标系）答案
1. D 2.A 3.D 4.B 5.D 6. B 7.s和 t；v 8.x≥13
9. 8 10.I=32∕R 11. 0.7,2.2 12. -1 13.（9，12）
14.以火车站为原点，以正东、正北方向为X轴、Y轴的正方向，建立平面直角坐标系，火车站
（0，0） 体育场（-400，200） 华侨宾馆（-300，-200） 百佳超市（200，-300）
15. （1）上午9点；（2）30千米；（3）15千米/小时；（4）略
第12课 一次函数答案
1.y=-3/4x+1/3 2.y=3x+5,y=-x-10 3.y=25-x(015.y=5x-3, (2)-5.5 ,(3)y=5x-23
16.(1)60米， (2)300米, 小强 (3)8分钟
17.(1)y=16-2x(0≤x≤4) (2)不存在.(当y=3时,16-x=3即x=6.5不在0≤x≤4之间) 18.0得不等式组,解之可得) 19.y=x+1,0.5
第13课反比例函数答案
1.－6 2. y = 3.　12 4. －1 5.　 3 6.y = －(x<0) 7. =
8. A 　9. D 10. S△AOB=12 11. (1)A (3,3) (2) y=
12. 反比例函数解析式y=－ ；一次函数解析式y=2x+10或y =－x+
13.y=2x－ 14. (1)k =1 (2)一次函数解析式y=－x+4 ；反比例函数解析式y=－
15. (1)k=－2；m=2 (2)∠ACO=30°；∣AO∣:∣AC∣ =: 4
第14课二次函数答案
1. (－6, 0 ) ；(1 , 0) ；(0 , －6) 2. 2 　3.y =3(x+1)2+9；(－1 ,9) ；
直线x=－1；x<－1 4.－12 5. 6. (6 , 0 )　 7.B 8.D
9.C 10.D 11.D 12.B
13. (1)y= －x2+2x+3； (2)y=2(x－3)2 －1 ；(3)y=－(x－6)2+3或y= (x－6)2 – 3
14.（1）y= － x2 +6x – 5 ,A(3,4) ； (2)原点O到直线AB的距离为
15.（1）y = -x2+2x+8 ； (2)y OE = 2x
第15课函数的应用（1）答案
1．在19.9~22之间（不包括19.9和22）均可
2．(0≤t≤2)
3．当路程s一定时，速度v是时间t的反比例函数；（s是常数，s≠0）
4．6 5．
6．或或或
7．C 8．D
9．解：.
∵，∴. ∴自变量x的取值范围是.
10．解：（1）农民自带的零钱是5元.
（2）（元）.
答：降价前他每千克土豆卖0.5元.
（3）（千克）.
答：他一共带了45千克土豆.
11．.解：（1）1，150，300.
（2）根据图象提供的信息，可知点M为ON的中点，MK∥NE，
∴. ∴，即轿车追上货车需1.5小时.
（3）根据图象提供的信息，可知M为CD的中点，且MK∥DF，
∴K是CF的中点. ∴CF=3. ∴.
　　　 ∴，即轿车比货车早到1小时.
第16课 函数的应用(2)答案
1． 2． 3．
4．（1）图象都是抛物线；（2）开口向上；（3）都有最低点（或最小值）
5．A 6．B
7．解：（1）160×0.7=112（万米3）；
（2）；
（3）当时，. 解得（天）
答：需要150天.
8．解：（1）；（2）每名运动员需支付56元.
9．解：（1）设，∵点（0.1，1000）在这个函数的图象上，
∴. ∴k=100.
∴p与S的函数关系式为.
（2）当S=0.5m2时，（Pa）.
10．解：（1）由于顶点在y轴上，所以设这部分抛物线为图象的函数的解析式为.
因为点或在抛物线上，所以，得.
因此所求函数解析式为（≤x≤）.
（2）因为点D、E的纵坐标为，所以，得.
所以点D的坐标为，点E的坐标为.
所以.
因此卢浦大桥拱内实际桥长为（米）
第三单元 函数检测卷答案
1． 选择题
1．D 　 2．B 　 3．C 　 4．A 5．A 6．A
7．A 8．B 9．C 10．A 11．C 12．C
二．填空题
13．1,2 14．1 15．答案不唯一符合条件即可 16．25 17．y=-12/x 　18．（,0）
三．解答题
19．（1）略 　（2）y=-x 20．（1）-3 （2）略 （3）14
21．解：(1)过点A作AD⊥x轴，垂足为D
则OD=OA cos60°=2×=1，
∴点A的坐标为(1，)
（2）设直线AB的解析式为y=kx+b，
则有
∴直线AB的解析式为
令x=0,得，∴
22．（1），y=－x－1 （2）x<－2或023．解：(1)当0≤x≤5时，设y=kx，
由x=5时，y=5
得5=5k ∴k=1
∴0≤x≤5时，y=x
(2)当x≥5时，设y=k1x+6
由图象可知
5=5k1+b
l2.5=10k1+b
k1=1.5
b= -2.5
∴ 当x≥5时，y=1.5x-2.5
当x=8时，y=1.5×8—2.5=9.5(元)
24．（1）yA=0.4X , yB=-0.2X2+1.6X （2）投资A种产品7万元，B种产品3万元，这样投资可以获得最大利润5.8万元.
25. 解：（1） 由已知：OC=0.6，AC=0.6， 得点A的坐标为（0.6，0.6），
代入y=ax2，得a=， ∴抛物线的解析式为y=x2.
（2）点D1，D2的横坐标分别为0.2，0.4，
代入y=x2，得点D1，D2的纵坐标分别为：y1=×0.22≈0.07，y2=×0.42≈0.27，
∴立柱C1D1=0.6－0.07=0.53，C2D2=0.6－0.27=0.33，
由于抛物线关于y轴对称，栅栏所需立柱的总长度为：
2（C1D1+ C2D2）+OC=2（0.53+0.33）+0.6≈2.3米.
26．解：（1））
（2）销售价定位30元/千克时
）
∴ 这天销售利润是660元
（3）设一次进货最多千克
∴一次进货最多不能超过1518千克
27.解：(1)OA=6，OB=12 点C是线段AB的中点，OC=AC
作CE⊥x轴于点E．
∴ OE=OA=3，CE=OB=6．
∴ 点C的坐标为(3，6)
(2)作DF⊥x轴于点F
△OFD∽△OEC，=，于是可求得OF=2，DF=4．
∴ 点D的坐标为(2，4) 设直线AD的解析式为y=kx+b．
把A(6，0)，D(2，4)代人得 解得
∴ 直线AD的解析式为y=-x+6
Q1(-3，3) Q2(3，-3)
Q3(3，-3)
Q4(6，6)
数与代数综合检测卷(一)答案
1.a2+│b│； 2.－1.5×10-6，1.25×108 3.x7 ； 4.（a+1）（a－1）；
5.　1； 6.y=x2－1； 7.　4； 8.x≥3且x≠4； 9.a≥－且a≠2；
10.　 2，1.2； 11.B 12.C 13.C 14.A
15.A 16.D 17.A 18.A 19.C 20.C
21.－1； 22.16x2ny4+7yn+2, 23.， 24.， 25.x1=-2;x2=1,
26.-129. (1) ①略②y=-2x+14；(2) ①p=-2(x-7)2+50,当x=7时，p有最大值为50元；②画图略，2≤x≤12；0≤p≤50.
数与代数综合检测卷（二）答案
1．B； 2.A； 3.C； 4．D； 5．D； 7．C； 8．B； 9．D； 10．B；
11．3；　12．144；　　13． 14．； 　15．2； 16．8;
17. （１） (2)x＝3 ； 18.(1) ,(2) ； 19.（1）20；图略；（2）1725．
20．20、解：设饼干的标价每盒x元，牛奶的标价为每袋y元，
则 　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
由②得y=9.2－0.9x ④　　
把④代入①，得x+9.2－0.9x＞10
∴ x ＞8　
由③得8＜x＜10
∵x是整数 ∴x=9　　
将 x=9代入④，得 y=9.2－0.9×9=1.1　　
答 ：饼干一盒标价9元，一袋牛奶标价1.1元．
21． (1) 由题意，去A超市购买n副球拍和kn个乒乓球的费用为0.9(20n+kn)元，去B超市购买n副球拍和kn个乒乓球的费用为[20n+ n(k－3)]元，
由0.9(20n+kn)< 20n+ n (k－3)，解得 k>10；
由0.9(20n+kn)= 20n+n (k－3)，解得 k=10；
由0.9(20n+kn)> 20n+n (k－3)，解得 k<10.
∴ 当k>10时，去A超市购买更合算；当k=10时，去A、B两家超市购买都一样；当3≤k<10时，去B超市购买更合算.
(2) 当k=12时，购买n副球拍应配12n个乒乓球.
若只在A超市购买，则费用为0.9(20n+12n)=28.8n(元)
若只在B超市购买，则费用为20n+(12n-3n)=29n(元)
若在B超市购买n副球拍，然后再在A超市购买不足的乒乓球，
则费用为20n+0.9×(12-3)n=28.1n(元)
显然，28.1n<28.8n <29n.
∴ 最省钱的购买方案为：在B超市购买n副球拍同时获得送的3n个乒乓球，然后在A超市按九折购买9n个乒乓球.
22．解：（1））
（2）销售价定位30元/千克时
）
∴ 这天销售利润是660元
（3）设一次进货最多千克
∴一次进货最多不能超过1518千克
23.解：(1)OA=6，OB=12 点C是线段AB的中点，OC=AC
作CE⊥x轴于点E．
∴ OE=OA=3，CE=OB=6．
∴ 点C的坐标为(3，6)
(2)作DF⊥x轴于点F
△OFD∽△OEC，=，于是可求得OF=2，DF=4．
∴ 点D的坐标为(2，4) 设直线AD的解析式为y=kx+b．
把A(6，0)，D(2，4)代人得 解得
∴ 直线AD的解析式为y=-x+6
Q1(-3，3) Q2(3，-3)
Q3(3，-3)
Q4(6，6)
A
B
C
D
P
时刻t（时） 0 4 8 12 16 20 24
温度T（℃） 16 18.1 19.9 22 19 17.2
第5题图
（第6题）
第9题图
第12题图
O
x
y
O
x
y
O
x
y
O
x
y
A
B
C
D
O
A
B
x
y
x
O
y
x
O
y
x
O
y
x
O
y
A
B
C
D
O
x(元)
y(件)
·
·
·
·
·
·
·
·
·
-2
·
·
·
·
·
·
2
·
2
-2
·
·
·
·
·
O
x(元)
y(件)
·
·
·
·
·
·
·
·
·
-6
·
·
·
·
·
·
6
·
6
-6
·
·
·
·
·
40%
12题
14题
15题
26
13
44
11
第一次
F②
第二次
F①
第三次
F②
…
小朋友，本来你用10元钱买一盒饼干是够的，但要再买一袋牛奶就不够了！今天是儿童节，我给你买的饼干打9折，两样东西请拿好！还有找你的8角钱．
一盒饼干的标价可是整数元哦！
阿姨，我买一盒饼干和一袋牛奶（递上10元钱）
0
3
4
0.7
1
y(元)
x(分)

A
B
O
x
y
O
A
第7题图
y
O
D
C
x
A
B
第6题图
y
M
x
O
第3题图
第11题图
O
y
x
B
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
C
D
O
O
O
O
y
y
y
y
x
x
x
x
O
O
-1
y
L
x
第15题图
① ② ③
PAGE