人教版七年级数学下册第七章平面直角坐标系单元复习题 (含解析)
文档属性
| 名称 | 人教版七年级数学下册第七章平面直角坐标系单元复习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 458.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 10:56:39 | ||
图片预览


文档简介
人教版七年级数学下册第七章平面直角坐标系 单元复习题
一、选择题
1.会议室2排3号记作(2,3),那么3排2号记作( )
A.(3,2) B.(2,3) C.(-3,-2) D.(-2,-3)
2.平面直角坐标系中,点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.根据下列表述,能确定位置的是( )
A.某电影院2排 B.大桥南路
C.北偏东 D.东经,北纬
4.已知点A(a﹣1,3)点B(﹣3,a+1),且直线AB∥y轴,则a的值为( )
A.1 B.﹣1 C.2 D.﹣2
5.如图,小明从点O出发,先向西走400m,再向南走300m到达点M,如果点M的位置用(﹣4,﹣3)表示,那么(1,2)表示的位置是( )
A.点A B.点B C.点C D.点D
6.如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(﹣3,﹣3)
C.(﹣6,4) D.(2,﹣5)
7.点P在第四象限,点P到x轴的距离是5,到y轴的距离是2,那么点P的坐标为( )
A. B. C. D.
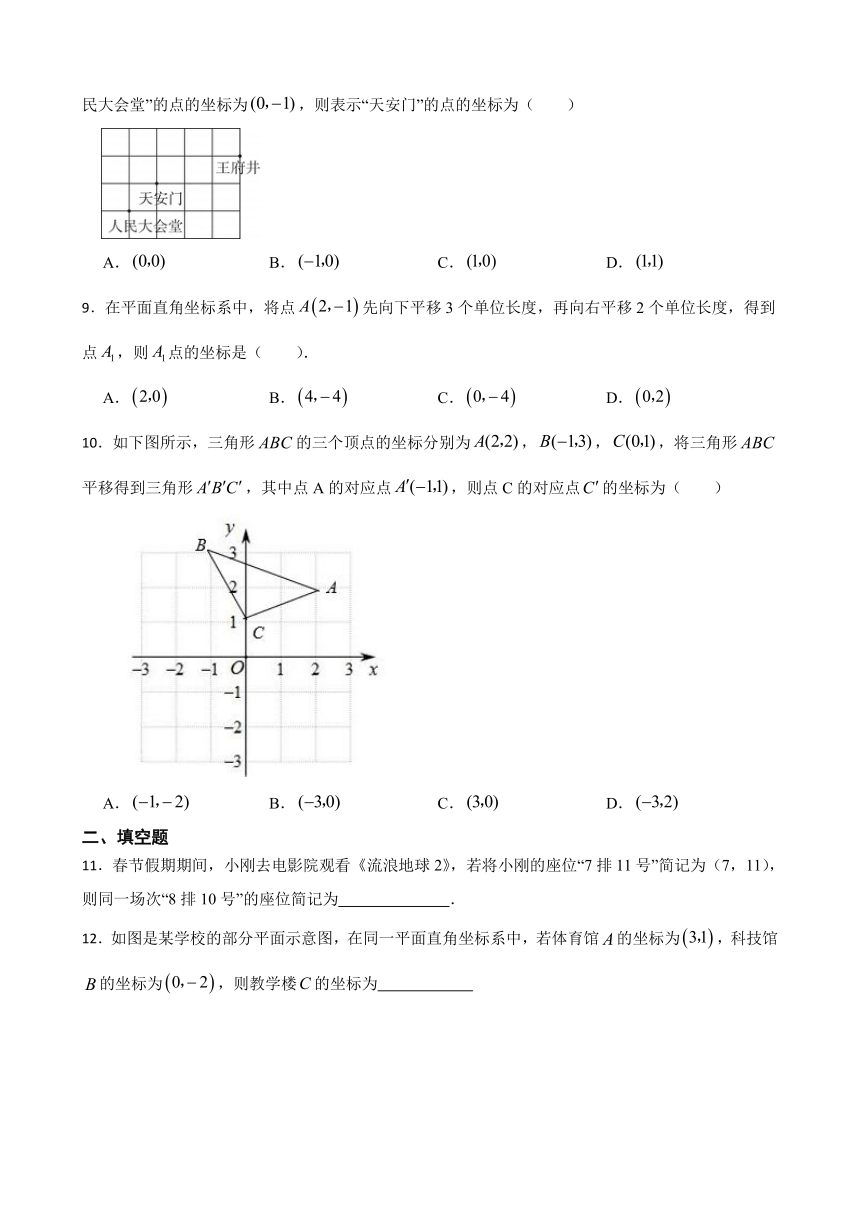
8.如图是天安门广场周围的景点分布示意图的一部分,若表示“王府井”的点的坐标为,表示“人民大会堂”的点的坐标为,则表示“天安门”的点的坐标为( )
A. B. C. D.
9.在平面直角坐标系中,将点先向下平移3个单位长度,再向右平移2个单位长度,得到点,则点的坐标是( ).
A. B. C. D.
10.如下图所示,三角形的三个顶点的坐标分别为,,,将三角形平移得到三角形,其中点A的对应点,则点C的对应点的坐标为( )
A. B. C. D.
二、填空题
11.春节假期期间,小刚去电影院观看《流浪地球2》,若将小刚的座位“7排11号”简记为(7,11),则同一场次“8排10号”的座位简记为 .
12.如图是某学校的部分平面示意图,在同一平面直角坐标系中,若体育馆的坐标为,科技馆的坐标为,则教学楼的坐标为
13.已知点到x轴的距离是 ,到y轴的距离是 .
14.将点向右平移2个单位长度,再向下平移3个单位长度得到点,则= .
三、解答题
15.已知平面直角坐标系内的点P(3-a,2a+9)到两个坐标轴的距离相等,求点P的坐标.
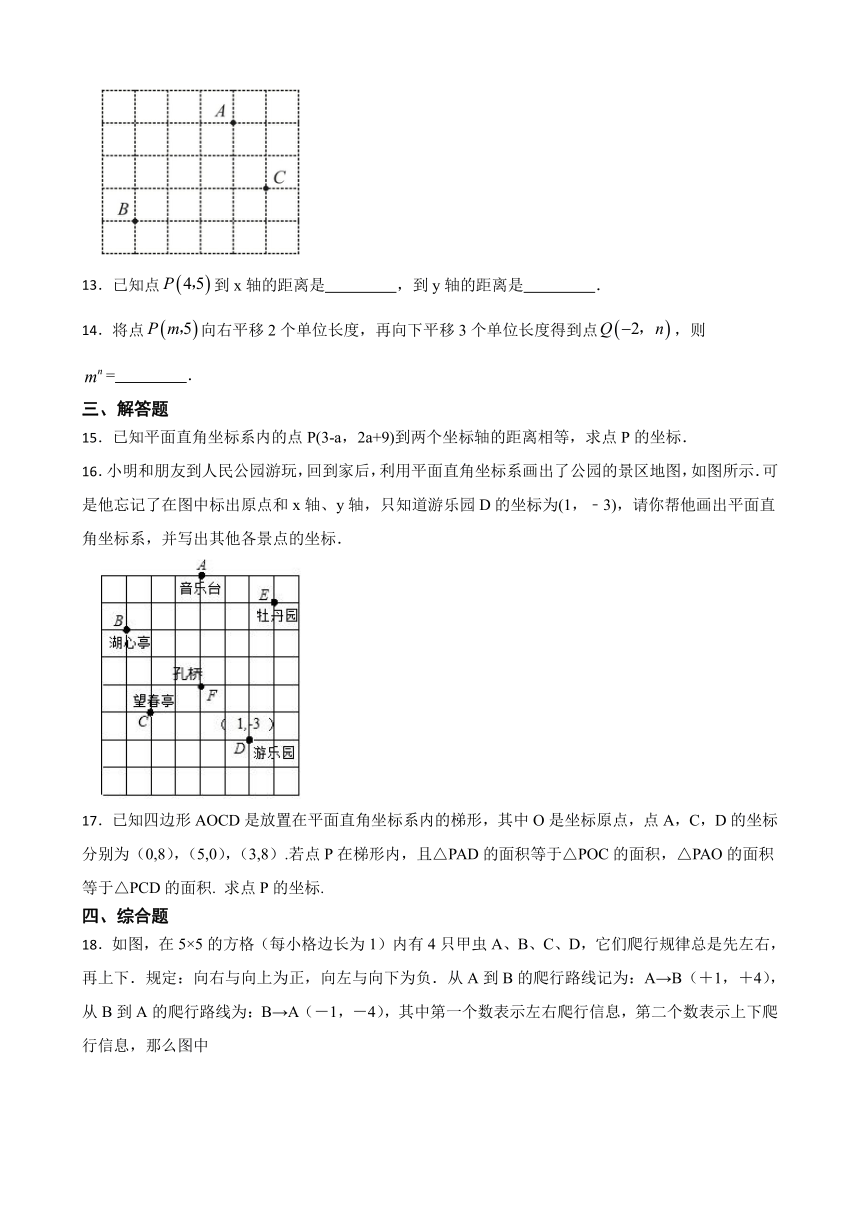
16.小明和朋友到人民公园游玩,回到家后,利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(1,﹣3),请你帮他画出平面直角坐标系,并写出其他各景点的坐标.
17.已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积. 求点P的坐标.
四、综合题
18.如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息,那么图中
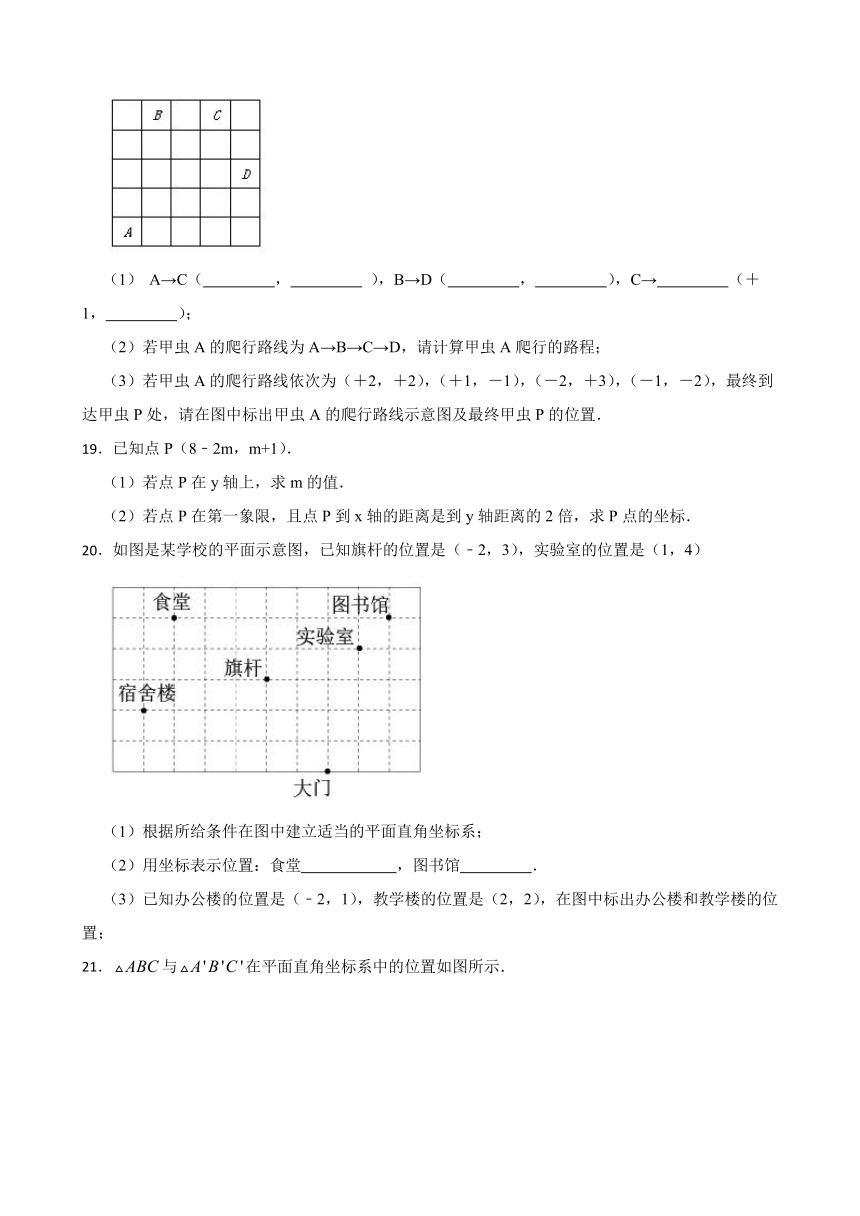
(1) A→C( , ),B→D( , ),C→ (+1, );
(2)若甲虫A的爬行路线为A→B→C→D,请计算甲虫A爬行的路程;
(3)若甲虫A的爬行路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),最终到达甲虫P处,请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置.
19.已知点P(8﹣2m,m+1).
(1)若点P在y轴上,求m的值.
(2)若点P在第一象限,且点P到x轴的距离是到y轴距离的2倍,求P点的坐标.
20.如图是某学校的平面示意图,已知旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(1)根据所给条件在图中建立适当的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 .
(3)已知办公楼的位置是(﹣2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
21.与在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ,A' ;
(2)若点是内部一点,则内部的对应点的坐标为 ;
(3)是由经过怎样的平移得到的?
答案解析部分
1.【答案】A
【解析】【解答】因为会议室2排3号记作(2,3),所以3排2号可以记作(3,2)。
故答案为:A
【分析】根据题干中的记数方法及规则求解即可。
2.【答案】D
【解析】【解答】解:∵8>0,-3<0,
∴点在 第四象限,
故答案为:D.
【分析】根据题意先求出8>0,-3<0,再判断象限即可。
3.【答案】D
【解析】【解答】解: A:某电影院2排,不能确定具体位置,不符合题意;
B:大桥南路,不能确定具体位置,不符合题意;
C:北偏东,不能确定具体位置,不符合题意;
D:东经,北纬,能确定具体位置,符合题意;
故答案为:D.
【分析】根据坐标的定义,确定位置需要两个数据,再对每个选项一一判断即可。
4.【答案】D
【解析】【解答】解:∵ 点A(a﹣1,3)点B(﹣3,a+1),且直线AB∥y轴,
∴a-1=-3,
∴a=-2.
故答案为:D.
【分析】根据平行于y轴的直线上所有点的横坐标相同可列出关于字母a的方程,求解即可.
5.【答案】B
【解析】【解答】解:∵点M的位置用( 4, 3)表示,实际意义为从点O出发,先向西走400m,再向南走300m,也就是网格中一个小正方形边长为100m,
∴(1,2)表示的位置实际意义为先向东走100m,再向北走200m,对应的是点B,
故答案为:B.
【分析】根据有序数对的表示方法求解即可。
6.【答案】D
【解析】【解答】解:由数轴可得:小手盖住的点位于第四象限,则(2,-5)可能为小手盖住的点.
故答案为:D.
【分析】由数轴可得:小手盖住的点位于第四象限,然后根据第四象限内的点:横坐标为正,纵坐标为负进行判断.
7.【答案】D
【解析】【解答】解:∵点P到x轴的距离是5,到y轴的距离是2,
∴点P横坐标的绝对值为2,纵坐标的绝对值为5,
∵点P在第四象限,
∴点P坐标为,
故答案为:D
【分析】先根据“点P到x轴的距离是5,到y轴的距离是2”即可得到点P横坐标的绝对值为2,纵坐标的绝对值为5,再根据象限内点坐标的特征即可求解。
8.【答案】C
【解析】【解答】解:建立如图所示坐标系,可得“天安门”的坐标为(1,0).
故答案为:C.
【分析】根据:王府井、“人民大会堂”的位置建立直角坐标系,结合“天安门”的位置可得相应的坐标.
9.【答案】B
【解析】【解答】点A向下平移3个单位后为(2,-1-3),即(2,-4),再将其向右平移2个单位后为(2+2,-4),即(4,-4),所以点的坐标为,
故答案为:B.
【分析】利用点坐标平移的特征:左减右加,上加下减求解即可。
10.【答案】B
【解析】【解答】∵,且平移后点A的对应点,
∴△ABC先向左平移3个单位,再向下平移1个单位,
∵C(0,1),
∴C'(0-3,1-1),即得(-3,0)
故答案为:B.
【分析】由平移后点A的对应点坐标,可确定△ABC的平移方向和距离,根据点的坐标平移规律:左减右加,上加下减进行解答即可.
11.【答案】(8,10)
【解析】【解答】解:∵将小刚的座位“7排11号”简记为(7,11),
∴同一场次“8排10号”的座位简记为 (8,10),
故答案为:(8,10).
【分析】根据 将小刚的座位“7排11号”简记为(7,11),求解即可。
12.【答案】
【解析】【解答】解:∵,,
∴建立如下图所示的坐标系,
根据坐标系可得:.
故答案为:.
【分析】将点B向上平移2个单位长度后的对应点为原点建立直角坐标系,进而根据点c的位置可得点C的坐标.
13.【答案】5;4
【解析】【解答】∵点P的坐标为(4,5),
∴点P到x轴的距离为5,点P到y轴的距离为4,
故答案为:5,4。
【分析】利用点坐标的定义求解即可。
14.【答案】16
【解析】【解答】解:点先向右平移2个单位长度,再向下平移3个单位长度后得到点,
∴,解得:,
∴.
故答案为:16.
【分析】利用点坐标平移的特征:左减右加,上加下减可得,求出,再将m、n的值代入计算即可。
15.【答案】解∵点P(3-a ,2a+9)到两个坐标轴的距离相等,
∴3-a=2a+9或3-a+2a+9=0,
解得a=-2或a=-12.
当a=-2时,3-a=5,2a+9=5,
此时,点P的坐标为(5,5);
当a=-12时,3-a=15,2a+9=-15,
此时,点P的坐标为(15,-15).
综上所述,点P的坐标为(5,5)或(15,-15).
【解析】【分析】先求出 3-a=2a+9或3-a+2a+9=0, 再求出 a=-2或a=-12 ,最后分类讨论,求点的坐标即可。
16.【答案】解:如图所示:A(﹣1,3),B(﹣4,1),C(﹣3,﹣2),E(2,2),F(﹣1,1).
【解析】【分析】根据点D的坐标建立平面直角坐标系,再根据平面直角坐标系直接求解即可。
17.【答案】解:如图,过点P作PE⊥y轴于点E.
因为:点A,C,D的坐标分别为(0,8),(5,0),(3,8),△PAD的面积等于△POC的面积,
所以: ×3AE= ×5OE,即3(8-OE)=5OE,
解得:OE=3
所以:△PAD的面积=△POC的面积= ×3×5=7.5,
△PAO的面积=△PCD的面积=[﹙3﹢5﹚×8÷2-2×7.5]÷2=8.5,
则 ×8PE=8.5,即PE= ,
所以:点P的坐标是( ,3).
【解析】【分析】根据题意画出图形,过点P作PE⊥y轴于点E,利用△PAD的面积等于△POC的面积,得出EO的长,进而得出PE的长,即可得出P点坐标.
18.【答案】(1)+3;+4;+3;-2;D;-2
(2)解:据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);则该甲虫走过的路线长为1+4+2+0+1+2=10.
答:甲虫A爬行的路程为10;
(3)
【解析】【分析】(1)根据第一个数表示左右方向,第二个数表示上下方向结合图形写出即可;
(2)根据行走路线列出算式计算即可得解;
(3)根据方格和标记方法作出线路图即可得解。
19.【答案】(1)解:∵点P(8﹣2m,m+1),点P在y轴上,
∴8﹣2m=0,
解得:m=4;
(2)解:由题意可得:m+1=2(8﹣2m),
解得:m=3,
则8﹣2m=2,m+1=4,
故P(2,4).
【解析】【分析】(1)根据题意先求出 8﹣2m=0, 再求解即可;
(2)根据题意先求出 m+1=2(8﹣2m), 再求出m=3,最后代入计算求解即可。
20.【答案】(1)解:如图,以大门为坐标原点建立坐标系,
则满足旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(2)(-5,5);(2,5)
(3)解:根据办公楼的位置是(﹣2,1),教学楼的位置是(2,2),描点如图所示
【解析】【分析】(1)根据“旗杆”和“实验室”的坐标直接建立平面直角坐标系即可;
(2)根据平面直角坐标系直接写出“食堂”和“图书馆”的坐标即可;
(3)在平面直角坐标系中直接写出“办公楼”和“教学楼”的位置即可。
21.【答案】(1)(1,3);(-3,1)
(2)
(3)解:∵点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为(x-4,y-2),
∴△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C'.
【解析】【解答】解:(1)由题意可得:A(1,3),A'(-3,1),
故答案为:(1,3),(-3,1);
(2)根据题意可得:△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C',
∴点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为(x-4,y-2);
故答案为:(x-4,y-2);
【分析】(1)根据两点在平面直角坐标系中的位置读出其坐标即可;
(2)由A与A'的坐标,得出平移规律:△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C',进而根据图形的平移与点的坐标的规律:左减右加,上加下减,可得点P'的坐标;
(3)根据(2)找到的规律即可得到答案.
一、选择题
1.会议室2排3号记作(2,3),那么3排2号记作( )
A.(3,2) B.(2,3) C.(-3,-2) D.(-2,-3)
2.平面直角坐标系中,点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.根据下列表述,能确定位置的是( )
A.某电影院2排 B.大桥南路
C.北偏东 D.东经,北纬
4.已知点A(a﹣1,3)点B(﹣3,a+1),且直线AB∥y轴,则a的值为( )
A.1 B.﹣1 C.2 D.﹣2
5.如图,小明从点O出发,先向西走400m,再向南走300m到达点M,如果点M的位置用(﹣4,﹣3)表示,那么(1,2)表示的位置是( )
A.点A B.点B C.点C D.点D
6.如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(﹣3,﹣3)
C.(﹣6,4) D.(2,﹣5)
7.点P在第四象限,点P到x轴的距离是5,到y轴的距离是2,那么点P的坐标为( )
A. B. C. D.
8.如图是天安门广场周围的景点分布示意图的一部分,若表示“王府井”的点的坐标为,表示“人民大会堂”的点的坐标为,则表示“天安门”的点的坐标为( )
A. B. C. D.
9.在平面直角坐标系中,将点先向下平移3个单位长度,再向右平移2个单位长度,得到点,则点的坐标是( ).
A. B. C. D.
10.如下图所示,三角形的三个顶点的坐标分别为,,,将三角形平移得到三角形,其中点A的对应点,则点C的对应点的坐标为( )
A. B. C. D.
二、填空题
11.春节假期期间,小刚去电影院观看《流浪地球2》,若将小刚的座位“7排11号”简记为(7,11),则同一场次“8排10号”的座位简记为 .
12.如图是某学校的部分平面示意图,在同一平面直角坐标系中,若体育馆的坐标为,科技馆的坐标为,则教学楼的坐标为
13.已知点到x轴的距离是 ,到y轴的距离是 .
14.将点向右平移2个单位长度,再向下平移3个单位长度得到点,则= .
三、解答题
15.已知平面直角坐标系内的点P(3-a,2a+9)到两个坐标轴的距离相等,求点P的坐标.
16.小明和朋友到人民公园游玩,回到家后,利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(1,﹣3),请你帮他画出平面直角坐标系,并写出其他各景点的坐标.
17.已知四边形AOCD是放置在平面直角坐标系内的梯形,其中O是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且△PAD的面积等于△POC的面积,△PAO的面积等于△PCD的面积. 求点P的坐标.
四、综合题
18.如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息,那么图中
(1) A→C( , ),B→D( , ),C→ (+1, );
(2)若甲虫A的爬行路线为A→B→C→D,请计算甲虫A爬行的路程;
(3)若甲虫A的爬行路线依次为(+2,+2),(+1,-1),(-2,+3),(-1,-2),最终到达甲虫P处,请在图中标出甲虫A的爬行路线示意图及最终甲虫P的位置.
19.已知点P(8﹣2m,m+1).
(1)若点P在y轴上,求m的值.
(2)若点P在第一象限,且点P到x轴的距离是到y轴距离的2倍,求P点的坐标.
20.如图是某学校的平面示意图,已知旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(1)根据所给条件在图中建立适当的平面直角坐标系;
(2)用坐标表示位置:食堂 ,图书馆 .
(3)已知办公楼的位置是(﹣2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
21.与在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ,A' ;
(2)若点是内部一点,则内部的对应点的坐标为 ;
(3)是由经过怎样的平移得到的?
答案解析部分
1.【答案】A
【解析】【解答】因为会议室2排3号记作(2,3),所以3排2号可以记作(3,2)。
故答案为:A
【分析】根据题干中的记数方法及规则求解即可。
2.【答案】D
【解析】【解答】解:∵8>0,-3<0,
∴点在 第四象限,
故答案为:D.
【分析】根据题意先求出8>0,-3<0,再判断象限即可。
3.【答案】D
【解析】【解答】解: A:某电影院2排,不能确定具体位置,不符合题意;
B:大桥南路,不能确定具体位置,不符合题意;
C:北偏东,不能确定具体位置,不符合题意;
D:东经,北纬,能确定具体位置,符合题意;
故答案为:D.
【分析】根据坐标的定义,确定位置需要两个数据,再对每个选项一一判断即可。
4.【答案】D
【解析】【解答】解:∵ 点A(a﹣1,3)点B(﹣3,a+1),且直线AB∥y轴,
∴a-1=-3,
∴a=-2.
故答案为:D.
【分析】根据平行于y轴的直线上所有点的横坐标相同可列出关于字母a的方程,求解即可.
5.【答案】B
【解析】【解答】解:∵点M的位置用( 4, 3)表示,实际意义为从点O出发,先向西走400m,再向南走300m,也就是网格中一个小正方形边长为100m,
∴(1,2)表示的位置实际意义为先向东走100m,再向北走200m,对应的是点B,
故答案为:B.
【分析】根据有序数对的表示方法求解即可。
6.【答案】D
【解析】【解答】解:由数轴可得:小手盖住的点位于第四象限,则(2,-5)可能为小手盖住的点.
故答案为:D.
【分析】由数轴可得:小手盖住的点位于第四象限,然后根据第四象限内的点:横坐标为正,纵坐标为负进行判断.
7.【答案】D
【解析】【解答】解:∵点P到x轴的距离是5,到y轴的距离是2,
∴点P横坐标的绝对值为2,纵坐标的绝对值为5,
∵点P在第四象限,
∴点P坐标为,
故答案为:D
【分析】先根据“点P到x轴的距离是5,到y轴的距离是2”即可得到点P横坐标的绝对值为2,纵坐标的绝对值为5,再根据象限内点坐标的特征即可求解。
8.【答案】C
【解析】【解答】解:建立如图所示坐标系,可得“天安门”的坐标为(1,0).
故答案为:C.
【分析】根据:王府井、“人民大会堂”的位置建立直角坐标系,结合“天安门”的位置可得相应的坐标.
9.【答案】B
【解析】【解答】点A向下平移3个单位后为(2,-1-3),即(2,-4),再将其向右平移2个单位后为(2+2,-4),即(4,-4),所以点的坐标为,
故答案为:B.
【分析】利用点坐标平移的特征:左减右加,上加下减求解即可。
10.【答案】B
【解析】【解答】∵,且平移后点A的对应点,
∴△ABC先向左平移3个单位,再向下平移1个单位,
∵C(0,1),
∴C'(0-3,1-1),即得(-3,0)
故答案为:B.
【分析】由平移后点A的对应点坐标,可确定△ABC的平移方向和距离,根据点的坐标平移规律:左减右加,上加下减进行解答即可.
11.【答案】(8,10)
【解析】【解答】解:∵将小刚的座位“7排11号”简记为(7,11),
∴同一场次“8排10号”的座位简记为 (8,10),
故答案为:(8,10).
【分析】根据 将小刚的座位“7排11号”简记为(7,11),求解即可。
12.【答案】
【解析】【解答】解:∵,,
∴建立如下图所示的坐标系,
根据坐标系可得:.
故答案为:.
【分析】将点B向上平移2个单位长度后的对应点为原点建立直角坐标系,进而根据点c的位置可得点C的坐标.
13.【答案】5;4
【解析】【解答】∵点P的坐标为(4,5),
∴点P到x轴的距离为5,点P到y轴的距离为4,
故答案为:5,4。
【分析】利用点坐标的定义求解即可。
14.【答案】16
【解析】【解答】解:点先向右平移2个单位长度,再向下平移3个单位长度后得到点,
∴,解得:,
∴.
故答案为:16.
【分析】利用点坐标平移的特征:左减右加,上加下减可得,求出,再将m、n的值代入计算即可。
15.【答案】解∵点P(3-a ,2a+9)到两个坐标轴的距离相等,
∴3-a=2a+9或3-a+2a+9=0,
解得a=-2或a=-12.
当a=-2时,3-a=5,2a+9=5,
此时,点P的坐标为(5,5);
当a=-12时,3-a=15,2a+9=-15,
此时,点P的坐标为(15,-15).
综上所述,点P的坐标为(5,5)或(15,-15).
【解析】【分析】先求出 3-a=2a+9或3-a+2a+9=0, 再求出 a=-2或a=-12 ,最后分类讨论,求点的坐标即可。
16.【答案】解:如图所示:A(﹣1,3),B(﹣4,1),C(﹣3,﹣2),E(2,2),F(﹣1,1).
【解析】【分析】根据点D的坐标建立平面直角坐标系,再根据平面直角坐标系直接求解即可。
17.【答案】解:如图,过点P作PE⊥y轴于点E.
因为:点A,C,D的坐标分别为(0,8),(5,0),(3,8),△PAD的面积等于△POC的面积,
所以: ×3AE= ×5OE,即3(8-OE)=5OE,
解得:OE=3
所以:△PAD的面积=△POC的面积= ×3×5=7.5,
△PAO的面积=△PCD的面积=[﹙3﹢5﹚×8÷2-2×7.5]÷2=8.5,
则 ×8PE=8.5,即PE= ,
所以:点P的坐标是( ,3).
【解析】【分析】根据题意画出图形,过点P作PE⊥y轴于点E,利用△PAD的面积等于△POC的面积,得出EO的长,进而得出PE的长,即可得出P点坐标.
18.【答案】(1)+3;+4;+3;-2;D;-2
(2)解:据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);则该甲虫走过的路线长为1+4+2+0+1+2=10.
答:甲虫A爬行的路程为10;
(3)
【解析】【分析】(1)根据第一个数表示左右方向,第二个数表示上下方向结合图形写出即可;
(2)根据行走路线列出算式计算即可得解;
(3)根据方格和标记方法作出线路图即可得解。
19.【答案】(1)解:∵点P(8﹣2m,m+1),点P在y轴上,
∴8﹣2m=0,
解得:m=4;
(2)解:由题意可得:m+1=2(8﹣2m),
解得:m=3,
则8﹣2m=2,m+1=4,
故P(2,4).
【解析】【分析】(1)根据题意先求出 8﹣2m=0, 再求解即可;
(2)根据题意先求出 m+1=2(8﹣2m), 再求出m=3,最后代入计算求解即可。
20.【答案】(1)解:如图,以大门为坐标原点建立坐标系,
则满足旗杆的位置是(﹣2,3),实验室的位置是(1,4)
(2)(-5,5);(2,5)
(3)解:根据办公楼的位置是(﹣2,1),教学楼的位置是(2,2),描点如图所示
【解析】【分析】(1)根据“旗杆”和“实验室”的坐标直接建立平面直角坐标系即可;
(2)根据平面直角坐标系直接写出“食堂”和“图书馆”的坐标即可;
(3)在平面直角坐标系中直接写出“办公楼”和“教学楼”的位置即可。
21.【答案】(1)(1,3);(-3,1)
(2)
(3)解:∵点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为(x-4,y-2),
∴△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C'.
【解析】【解答】解:(1)由题意可得:A(1,3),A'(-3,1),
故答案为:(1,3),(-3,1);
(2)根据题意可得:△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C',
∴点P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为(x-4,y-2);
故答案为:(x-4,y-2);
【分析】(1)根据两点在平面直角坐标系中的位置读出其坐标即可;
(2)由A与A'的坐标,得出平移规律:△ABC向左平移4个单位,再向下平移2个单位得到△A'B'C',进而根据图形的平移与点的坐标的规律:左减右加,上加下减,可得点P'的坐标;
(3)根据(2)找到的规律即可得到答案.
