23.3解直角三角形复习课导学案
图片预览

文档简介
解直角三角形复习课学案
【学习目标】
1、探索直角三角形中锐角三角函数值与三边之间的关系.掌握三角函数定义
2、掌握30°、45°、60°等特殊角的三角函数值,并会进行有关特殊角的三角函数值的计算.
3、能综合运用直角三角形的勾股定理与边角关系解决实际问题,提高数学建模能力.
【重点】合理构造直角三角形、解直角三角形实际应用;
【难点】如何读懂题意对实际应用题进行建立方程解题;
一、生活问题:
(09·滨州)某楼梯侧面视图如图,其中A ( http: / / www.21cnjy.com )B=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应 。
二、知识点梳理:
3.解直角三角形的依据
(1)由直角三角形中已知 个元素求出另外 个元素的过程叫解直角三角形
三边关系:
(2)直角三角形中的边角关系 两锐角关系:
角与边的关系:sinA=
cosA=
tanA=
4. 锐角三角函数的特殊关系
锐角三角函数的恒正性:锐角三角函数值都是正实数,
即 0<sinA<1,0<cosA<1.
(2)余角关系:若A+B=90,
则 sinB= ,cosB= ,tanB= ,cotB= .
(3)平方关系:
(4)、倒数关系:tanA·cotA=1.或
(5)商式关系:
5、在解直角三角形及应用时经常接触到的一些概念
(1)仰角和俯角 (2)方位角 (3)斜坡的坡度
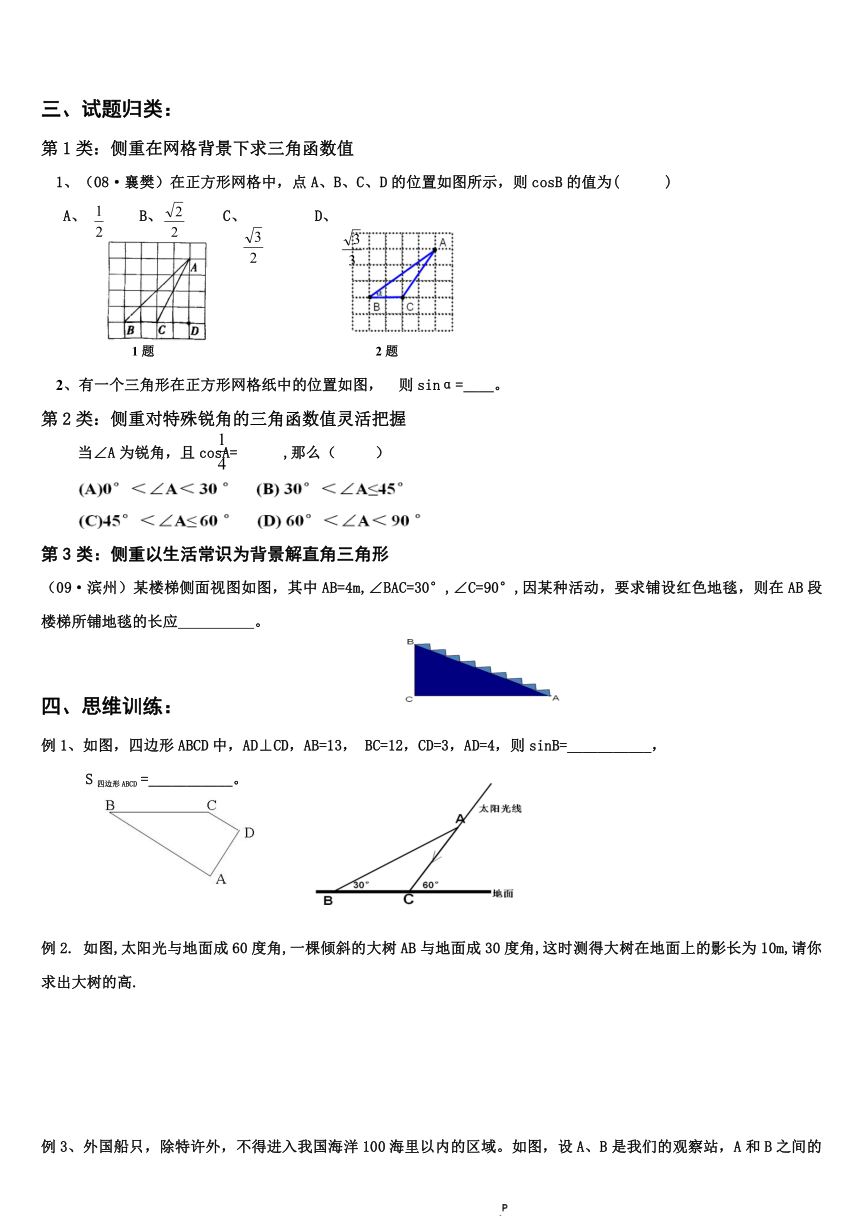
三、试题归类:
第1类:侧重在网格背景下求三角函数值
1、(08·襄樊)在正方形网格中,点A、B、C、D的位置如图所示,则cosB的值为( )
A、 B、 C、 D、
1题 2题
2、有一个三角形在正方形网格纸中的位置如图, 则sinα=____。
第2类:侧重对特殊锐角的三角函数值灵活把握
当∠A为锐角,且cosA= ,那么( )
第3类:侧重以生活常识为背景解直角三角形
(09·滨州)某楼梯侧面视图如图,其中AB ( http: / / www.21cnjy.com )=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应 。
四、思维训练:
例1、如图,四边形ABCD中,AD⊥CD,AB=13, BC=12,CD=3,AD=4,则sinB=___________,
S四边形ABCD =___________。
例2. 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
例3、外国船只,除特许外,不得进入我国海洋 ( http: / / www.21cnjy.com )100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在P点,在A点测得∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告,令其退出我国海域.
五、讨论交流:
1. 如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求△ABC的面积。
2、一渔船上的渔民在A处看 ( http: / / www.21cnjy.com )见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离 ?
【自我评价】
本节课满意度: ☆☆☆☆☆ ☆☆☆☆ ☆☆☆
六、中考练兵:
一、选择题(本题共5个小题,每小题只有一个选项符合要求,请将正确答案的标号填在括号中.)
1. (2008年庆阳市)正方形网格中,如图放置,则=( )
A. B. C. D.
第3题 第4题
2. (2008年江苏宿迁)已知为锐角,且,则等于( )
A. B. C. D.
3. (2008 山东 聊城)如图,在 ( http: / / www.21cnjy.com )平地上种植树时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.5的山坡上种植树,也要求株距为4m,那么相邻两树间的坡面距离约为( )
A.4.5m B.4.6m C.6m D.8m
4. (2009年浙江省)如图,把一块直角三角板的直角顶点放在直尺的一边上,
如果∠1=32o,那么∠2的度数是( )
A.32o B.58o C.68o D.60o
5. (2008年杭州市)在直角坐标系中,点在第一象限内,且与轴的正半轴的夹角为,则的值是( )
A. B. C.8 D.2
二、填空题(本题共3个小题,请将答案填在横线上.)
6.(2009年枣庄)17.如图,在菱形ABCD中,DE⊥AB于E,DE=6cm, 则菱形ABCD的面积是__________.
7.(茂名市2009年)如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的处目测得点 与甲、乙楼顶刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是 米.
8.( 浙江省2009年) “赵爽 ( http: / / www.21cnjy.com )弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于 .
9. (2011 甘肃兰州)某水库 ( http: / / www.21cnjy.com )大坝的横截面是梯形,坝内斜坡的坡度i=1:3,坝外斜坡的坡度i=1:1,则两个坡角的和为 .
三、解答题(本题共3个小题,解答应写出必要的问题说明或演算步骤.)
10. (2009张家界)计算:.
11.(2009年辽宁朝阳)一艘小船从码头出发,沿北偏东方向航行,航行一段时间到达小岛处后,又沿着北偏西方向航行了10海里到达处,这时从码头测得小船在码头北偏东的方向上,求此时小船与码头之间的距离(,结果保留整数).
.
12. (2008遵义)我市某乡镇学校教学楼 ( http: / / www.21cnjy.com )后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=600,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过450时,可确保山体不滑坡,改造时保持坡脚A 不动,从坡顶B 沿BC削进到E 处,问BE至少是多少米(结果保留根号)?
正弦:sinA=
余弦:cosA=
正切:tanA=
1锐角三角函数的意义
30° 45° 60°
sinα
cosα
tanα
2.特殊角的三角函数值
2
1
A
B
O
第1题
D
C
B
E
A
第6图
乙
C
B
A
甲
10米
?米
20米
α
B
A
C
53°
23°
22°
北
北
(第11题图)
【学习目标】
1、探索直角三角形中锐角三角函数值与三边之间的关系.掌握三角函数定义
2、掌握30°、45°、60°等特殊角的三角函数值,并会进行有关特殊角的三角函数值的计算.
3、能综合运用直角三角形的勾股定理与边角关系解决实际问题,提高数学建模能力.
【重点】合理构造直角三角形、解直角三角形实际应用;
【难点】如何读懂题意对实际应用题进行建立方程解题;
一、生活问题:
(09·滨州)某楼梯侧面视图如图,其中A ( http: / / www.21cnjy.com )B=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应 。
二、知识点梳理:
3.解直角三角形的依据
(1)由直角三角形中已知 个元素求出另外 个元素的过程叫解直角三角形
三边关系:
(2)直角三角形中的边角关系 两锐角关系:
角与边的关系:sinA=
cosA=
tanA=
4. 锐角三角函数的特殊关系
锐角三角函数的恒正性:锐角三角函数值都是正实数,
即 0<sinA<1,0<cosA<1.
(2)余角关系:若A+B=90,
则 sinB= ,cosB= ,tanB= ,cotB= .
(3)平方关系:
(4)、倒数关系:tanA·cotA=1.或
(5)商式关系:
5、在解直角三角形及应用时经常接触到的一些概念
(1)仰角和俯角 (2)方位角 (3)斜坡的坡度
三、试题归类:
第1类:侧重在网格背景下求三角函数值
1、(08·襄樊)在正方形网格中,点A、B、C、D的位置如图所示,则cosB的值为( )
A、 B、 C、 D、
1题 2题
2、有一个三角形在正方形网格纸中的位置如图, 则sinα=____。
第2类:侧重对特殊锐角的三角函数值灵活把握
当∠A为锐角,且cosA= ,那么( )
第3类:侧重以生活常识为背景解直角三角形
(09·滨州)某楼梯侧面视图如图,其中AB ( http: / / www.21cnjy.com )=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应 。
四、思维训练:
例1、如图,四边形ABCD中,AD⊥CD,AB=13, BC=12,CD=3,AD=4,则sinB=___________,
S四边形ABCD =___________。
例2. 如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
例3、外国船只,除特许外,不得进入我国海洋 ( http: / / www.21cnjy.com )100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在P点,在A点测得∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告,令其退出我国海域.
五、讨论交流:
1. 如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求△ABC的面积。
2、一渔船上的渔民在A处看 ( http: / / www.21cnjy.com )见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离 ?
【自我评价】
本节课满意度: ☆☆☆☆☆ ☆☆☆☆ ☆☆☆
六、中考练兵:
一、选择题(本题共5个小题,每小题只有一个选项符合要求,请将正确答案的标号填在括号中.)
1. (2008年庆阳市)正方形网格中,如图放置,则=( )
A. B. C. D.
第3题 第4题
2. (2008年江苏宿迁)已知为锐角,且,则等于( )
A. B. C. D.
3. (2008 山东 聊城)如图,在 ( http: / / www.21cnjy.com )平地上种植树时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.5的山坡上种植树,也要求株距为4m,那么相邻两树间的坡面距离约为( )
A.4.5m B.4.6m C.6m D.8m
4. (2009年浙江省)如图,把一块直角三角板的直角顶点放在直尺的一边上,
如果∠1=32o,那么∠2的度数是( )
A.32o B.58o C.68o D.60o
5. (2008年杭州市)在直角坐标系中,点在第一象限内,且与轴的正半轴的夹角为,则的值是( )
A. B. C.8 D.2
二、填空题(本题共3个小题,请将答案填在横线上.)
6.(2009年枣庄)17.如图,在菱形ABCD中,DE⊥AB于E,DE=6cm, 则菱形ABCD的面积是__________.
7.(茂名市2009年)如图,甲、乙两楼相距20米,甲楼高20米,小明站在距甲楼10米的处目测得点 与甲、乙楼顶刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是 米.
8.( 浙江省2009年) “赵爽 ( http: / / www.21cnjy.com )弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,则tanα的值等于 .
9. (2011 甘肃兰州)某水库 ( http: / / www.21cnjy.com )大坝的横截面是梯形,坝内斜坡的坡度i=1:3,坝外斜坡的坡度i=1:1,则两个坡角的和为 .
三、解答题(本题共3个小题,解答应写出必要的问题说明或演算步骤.)
10. (2009张家界)计算:.
11.(2009年辽宁朝阳)一艘小船从码头出发,沿北偏东方向航行,航行一段时间到达小岛处后,又沿着北偏西方向航行了10海里到达处,这时从码头测得小船在码头北偏东的方向上,求此时小船与码头之间的距离(,结果保留整数).
.
12. (2008遵义)我市某乡镇学校教学楼 ( http: / / www.21cnjy.com )后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=600,为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过450时,可确保山体不滑坡,改造时保持坡脚A 不动,从坡顶B 沿BC削进到E 处,问BE至少是多少米(结果保留根号)?
正弦:sinA=
余弦:cosA=
正切:tanA=
1锐角三角函数的意义
30° 45° 60°
sinα
cosα
tanα
2.特殊角的三角函数值
2
1
A
B
O
第1题
D
C
B
E
A
第6图
乙
C
B
A
甲
10米
?米
20米
α
B
A
C
53°
23°
22°
北
北
(第11题图)
