高中数学人教A版(2019)高一必修一5.1任意角和弧度制 学案(无答案)
文档属性
| 名称 | 高中数学人教A版(2019)高一必修一5.1任意角和弧度制 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 520.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 12:09:51 | ||
图片预览



文档简介
5.1 任意角和弧度制
●任意角
1.角的概念及其表示
角可以看成一条 绕着它的端点 所成的 .如图,
(1)始边:射线的 位置OA;
终边:射线的 位置OB;
顶点:射线的端点O.
(2)记法:图中的角α可记为“角α”或“∠α”或“∠AOB”.
2.任意角:我们把角的概念推广到了任意角,包括正角、负角和零角.
正角:一条射线绕其端点按 方向旋转形成的角
负角:一条射线绕其端点按 方向旋转形成的角
零角:一条射线 做任何旋转形成的角
3.角的相等
如果角α和角β的旋转方向相同且旋转量相等,那么就称 .
4.角的加法
设α,β是任意两个角,把角α的终边旋转角β,这时终边所对应的角是
.
5.相反角:把射线OA绕端点O按不同方向旋转相同的量所成的两个角
叫做互为 ,角α的相反角记为 ,α-β=α+ .
例题1:如图,射线OA先绕端点O逆时针方向旋转60°到OB处,再按顺时针方向旋转820°至OC处,则β= .
变式练习:
1、图①②中从OA旋转到OB,OB1,OB2时所成的角度α,β,γ分别是 , , .
6.象限角:
(1)我们通常在直角坐标系内讨论角,为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的 在第几象限,就说这个角是 限角.
(2)如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
注意:(1)锐角是第一象限角,钝角是第二象限角,直角的终边在坐标轴上,它不属于任何一个象限;
(2)每一个象限都有正角和负角,无法比较哪一个象限角的大小.
例题2: (多选)下列结论正确的有
A.-75°是第一象限角 B.225°是第三象限角
C.475°是第二象限角 D.-315°是第四象限角
变式练习: (多选)下列叙述不正确的是
A.三角形的内角是第一象限角或第二象限角
B.钝角是第二象限角
C.第二象限角比第一象限角大
D.小于180°的角是钝角、直角或锐角
6.终边相同的角
思考:给定一个角,它的终边是否唯一?若两角的终边相同,那么这两个角相等吗?
结论:给定一个角,它的终边 ;两角终边相同,这两个角 相等,比如30°角的终边和390°角的终边相同,它们正好相差了360°.
因此:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
例题3: 在与2 110°角终边相同的角中,求满足下列条件的角β.
(1)最大的负角;
(2)最小的正角;
(3)在360°~720°范围内的角.
归纳:终边相同的角的表示
(1)终边相同的角都可以表示成α+k·360°(k∈Z)的形式.
(2)终边相同的角相差360°的整数倍.
变式训练3:(1)写出终边在直线y=-x上的角的集合.
(2)与-2 024°角终边相同的最小正角是( )
A.136° B.132° C.58° D.42°
(3)若角2α与240°角的终边相同,则α等于( )
A.120°+k·360°,k∈Z
B.120°+k·180°,k∈Z
C.240°+k·360°,k∈Z
D.240°+k·180°,k∈Z
7.终边相同的角
思考 你能否表示出终边落在各个象限的角的集合?
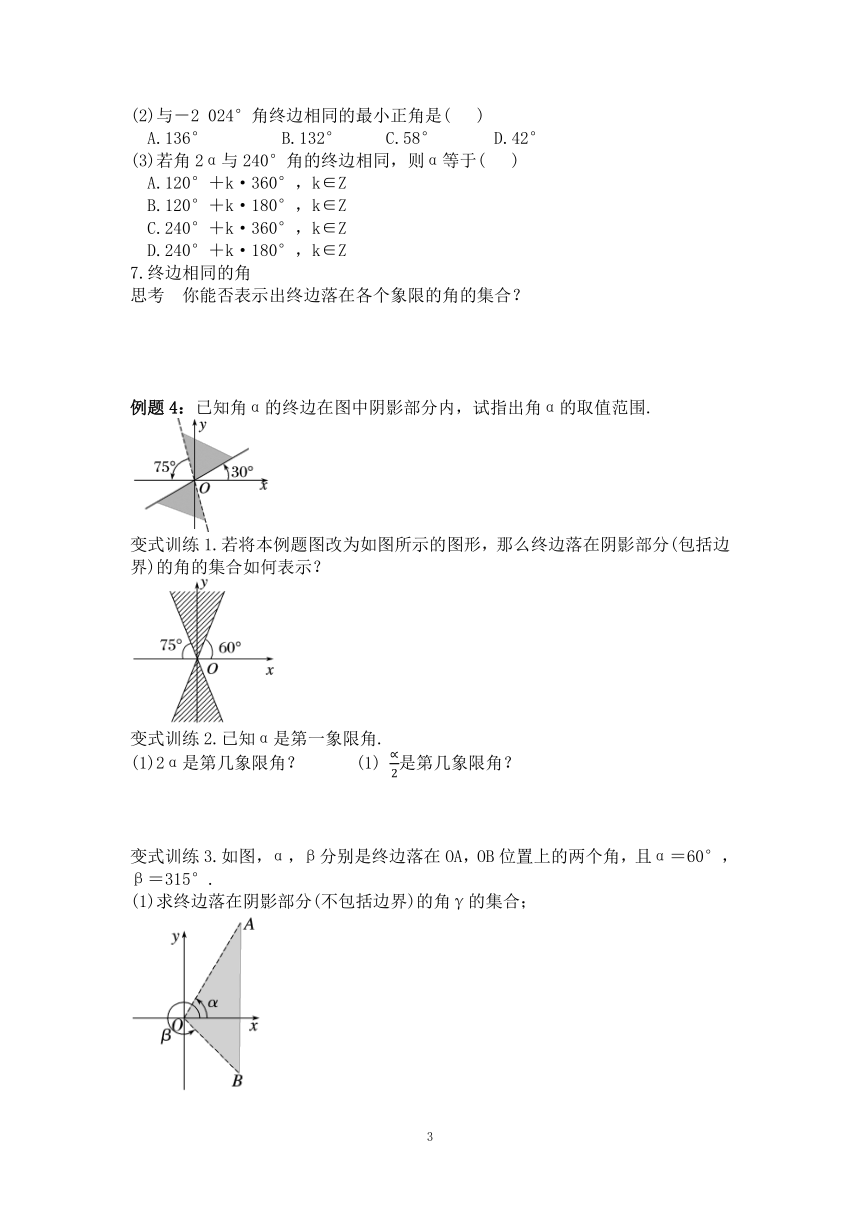
例题4:已知角α的终边在图中阴影部分内,试指出角α的取值范围.
变式训练1.若将本例题图改为如图所示的图形,那么终边落在阴影部分(包括边界)的角的集合如何表示?
变式训练2.已知α是第一象限角.
(1)2α是第几象限角? (1) 是第几象限角?
变式训练3.如图,α,β分别是终边落在OA,OB位置上的两个角,且α=60°,β=315°.
(1)求终边落在阴影部分(不包括边界)的角γ的集合;
(2)求终边落在阴影部分(不包括边界),且在0°~360°范围内的角θ的集合.
小结:1.知识清单:
(1)正角、负角、零角的概念.
(2)终边相同的角的表示.
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°的角的区别,终边相同角的表示中漏掉k∈Z.
当堂测试
1.已知集合A={第二象限角},B={钝角},C={小于180°的角},则A,B,C关系正确的是( )
A.B=A∩C B.A∪C=B
C.B∪C=C D.A=B=C
2.若α=45°+k·180°,k∈Z,则α的终边在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
3.亲爱的考生,我们数学考试完整的时间是2小时,则从考试开始到结束,钟表的分针转过的角度为 .
4.如图所示.终边落在阴影部分(包括边界)的角α的集合为 .
5.已知.
(1)写出与角终边相同的角的集合,并求出在内与角终边相同的角;
(2)若角与角终边相同,判断角是第几象限的角.
●弧度制
弧度制的概念
(1)思考:我们上节课所学习的角度制能否与实数建立一一对应的关系?
(2)度量角的两种制度
(3)弧度数的计算
注意:一定大小的圆心角α所对应的弧长和半径的比值是唯一确定的,与半径大小无关.
例题1:下列命题中,假命题是
A.“度”与“弧度”是度量角的两种不同的度量单位
B.1°的角是周角的,1 rad的角是周角的
C.1 rad的角比1°的角要大
D.用角度制和弧度制度量角,都与圆的半径有关
变式训练1.下列各命题中,真命题是
A.1弧度就是1°的圆心角所对的弧
B.1弧度是长度等于半径的弧
C.1弧度是1°的弧与1°的角之和
D.1弧度是长度等于半径长的弧所对的圆心角的大小
2.角度制与弧度制的互换
(1)思考:根据公式|α|=,你能得出圆周角的弧度数吗?
(2)弧度与角度的换算
.一些特殊角的度数与弧度数的对应关系
注意:(1)弧度单位rad可以省略;(2)在同一个题目中,弧度与角度不能混用
例题2:把下列角度化成弧度,弧度化成角度:
(1)37°30′; (2)-216°; (3)2 (4)
注意:角度与弧度换算技巧
在进行角度与弧度的换算时,抓住关系式π rad=180°是关键,由它可以得到:度数× =弧度数,弧度数× =度数.一般情况下,省略弧度单位rad.
变式训练:将下列角度与弧度进行互化:
(2)- (3)10° (4)-855°
3.利用弧度表示角
例题:将-1 125°角写成α+2kπ(k∈Z)的形式,其中0≤α<2π,并判断它是第几象限角?
变式:若在本例的条件下,在[-4π,4π]范围内找出与α终边相同的角的集合.
注意:用弧度制表示终边相同的角的两个关注点
(1)用弧度制表示终边相同的角α+2kπ(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍.
(2)注意同一题目中角度制与弧度制不能混用.
变式训练:(1)用弧度制表示所有与75°角终边相同的角的集合是
(2)将手表的分针拨快10分钟,则分针在旋转过程中形成的角的弧度数是
4.弧度制下扇形的弧长与面积公式
思考:(1)我们初中所学扇形的弧长和面积公式是什么?
(2)扇形的弧长与面积公式(R是扇形所在圆的半径,n°为扇形的圆心角)
例题:已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数.
变式训练:已知一扇形的周长为4,当它的半径与圆心角取何值时,扇形的面积最大?最大值是多少?
解题策略:(1)记公式:面积公式:S=lR=αR2,弧长公式:l=αR(其中l是扇形的弧长,R是扇形的半径,α是扇形圆心角的弧度数,0<α<2π).
涉及扇形的半径、周长、弧长、圆心角、面积等的计算问题,关键是分析题目中已知哪些量、要求哪些量,然后灵活运用弧长公式、扇形的面积公式直接求解或列方程(组)求解.变式训练 已知扇形的圆心角是α,半径为r,弧长为l.
变式训练:(1)若α=135°,r=10,求扇形的弧长l;
(2)若扇形AOB的周长为22,当扇形的圆心角α为多少弧度时,这个扇形的面积最大,并求出此时扇形的面积S的最大值.
小结:
1.知识清单:
(1)弧度制的概念.
(2)弧度与角度的相互转化.
(3)掌握特殊角的度数与弧度数的对应关系.
(4)扇形的弧长与面积的计算.
2.方法归纳:由特殊到一般、数学运算.
3.常见误区:弧度与角度易混用.
当堂测试
1.下列说法正确的是( )
A.1弧度的圆心角所对的弧长等于半径
B.大圆中1弧度的圆心角比小圆中1弧度的圆心角大
C.所有圆心角为1弧度的角所对的弧长都相等
D.用弧度表示的角都是正角
2.-660°等于( )
3.时钟的分针在1点到3点20分这段时间里转过的弧度为( )
4.已知一个扇形的弧长等于其所在圆半径的2倍,则该扇形圆心角的弧度数为 ,若该扇形的半径为1,则该扇形的面积为 .
5.已知角都是锐角,且角的终边与°角的终边相同,角的终边与670°角的终边相同,则______,______.
●任意角
1.角的概念及其表示
角可以看成一条 绕着它的端点 所成的 .如图,
(1)始边:射线的 位置OA;
终边:射线的 位置OB;
顶点:射线的端点O.
(2)记法:图中的角α可记为“角α”或“∠α”或“∠AOB”.
2.任意角:我们把角的概念推广到了任意角,包括正角、负角和零角.
正角:一条射线绕其端点按 方向旋转形成的角
负角:一条射线绕其端点按 方向旋转形成的角
零角:一条射线 做任何旋转形成的角
3.角的相等
如果角α和角β的旋转方向相同且旋转量相等,那么就称 .
4.角的加法
设α,β是任意两个角,把角α的终边旋转角β,这时终边所对应的角是
.
5.相反角:把射线OA绕端点O按不同方向旋转相同的量所成的两个角
叫做互为 ,角α的相反角记为 ,α-β=α+ .
例题1:如图,射线OA先绕端点O逆时针方向旋转60°到OB处,再按顺时针方向旋转820°至OC处,则β= .
变式练习:
1、图①②中从OA旋转到OB,OB1,OB2时所成的角度α,β,γ分别是 , , .
6.象限角:
(1)我们通常在直角坐标系内讨论角,为了方便,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,那么,角的 在第几象限,就说这个角是 限角.
(2)如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
注意:(1)锐角是第一象限角,钝角是第二象限角,直角的终边在坐标轴上,它不属于任何一个象限;
(2)每一个象限都有正角和负角,无法比较哪一个象限角的大小.
例题2: (多选)下列结论正确的有
A.-75°是第一象限角 B.225°是第三象限角
C.475°是第二象限角 D.-315°是第四象限角
变式练习: (多选)下列叙述不正确的是
A.三角形的内角是第一象限角或第二象限角
B.钝角是第二象限角
C.第二象限角比第一象限角大
D.小于180°的角是钝角、直角或锐角
6.终边相同的角
思考:给定一个角,它的终边是否唯一?若两角的终边相同,那么这两个角相等吗?
结论:给定一个角,它的终边 ;两角终边相同,这两个角 相等,比如30°角的终边和390°角的终边相同,它们正好相差了360°.
因此:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
例题3: 在与2 110°角终边相同的角中,求满足下列条件的角β.
(1)最大的负角;
(2)最小的正角;
(3)在360°~720°范围内的角.
归纳:终边相同的角的表示
(1)终边相同的角都可以表示成α+k·360°(k∈Z)的形式.
(2)终边相同的角相差360°的整数倍.
变式训练3:(1)写出终边在直线y=-x上的角的集合.
(2)与-2 024°角终边相同的最小正角是( )
A.136° B.132° C.58° D.42°
(3)若角2α与240°角的终边相同,则α等于( )
A.120°+k·360°,k∈Z
B.120°+k·180°,k∈Z
C.240°+k·360°,k∈Z
D.240°+k·180°,k∈Z
7.终边相同的角
思考 你能否表示出终边落在各个象限的角的集合?
例题4:已知角α的终边在图中阴影部分内,试指出角α的取值范围.
变式训练1.若将本例题图改为如图所示的图形,那么终边落在阴影部分(包括边界)的角的集合如何表示?
变式训练2.已知α是第一象限角.
(1)2α是第几象限角? (1) 是第几象限角?
变式训练3.如图,α,β分别是终边落在OA,OB位置上的两个角,且α=60°,β=315°.
(1)求终边落在阴影部分(不包括边界)的角γ的集合;
(2)求终边落在阴影部分(不包括边界),且在0°~360°范围内的角θ的集合.
小结:1.知识清单:
(1)正角、负角、零角的概念.
(2)终边相同的角的表示.
(3)象限角、区域角的表示.
2.方法归纳:数形结合、分类讨论.
3.常见误区:锐角与小于90°的角的区别,终边相同角的表示中漏掉k∈Z.
当堂测试
1.已知集合A={第二象限角},B={钝角},C={小于180°的角},则A,B,C关系正确的是( )
A.B=A∩C B.A∪C=B
C.B∪C=C D.A=B=C
2.若α=45°+k·180°,k∈Z,则α的终边在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
3.亲爱的考生,我们数学考试完整的时间是2小时,则从考试开始到结束,钟表的分针转过的角度为 .
4.如图所示.终边落在阴影部分(包括边界)的角α的集合为 .
5.已知.
(1)写出与角终边相同的角的集合,并求出在内与角终边相同的角;
(2)若角与角终边相同,判断角是第几象限的角.
●弧度制
弧度制的概念
(1)思考:我们上节课所学习的角度制能否与实数建立一一对应的关系?
(2)度量角的两种制度
(3)弧度数的计算
注意:一定大小的圆心角α所对应的弧长和半径的比值是唯一确定的,与半径大小无关.
例题1:下列命题中,假命题是
A.“度”与“弧度”是度量角的两种不同的度量单位
B.1°的角是周角的,1 rad的角是周角的
C.1 rad的角比1°的角要大
D.用角度制和弧度制度量角,都与圆的半径有关
变式训练1.下列各命题中,真命题是
A.1弧度就是1°的圆心角所对的弧
B.1弧度是长度等于半径的弧
C.1弧度是1°的弧与1°的角之和
D.1弧度是长度等于半径长的弧所对的圆心角的大小
2.角度制与弧度制的互换
(1)思考:根据公式|α|=,你能得出圆周角的弧度数吗?
(2)弧度与角度的换算
.一些特殊角的度数与弧度数的对应关系
注意:(1)弧度单位rad可以省略;(2)在同一个题目中,弧度与角度不能混用
例题2:把下列角度化成弧度,弧度化成角度:
(1)37°30′; (2)-216°; (3)2 (4)
注意:角度与弧度换算技巧
在进行角度与弧度的换算时,抓住关系式π rad=180°是关键,由它可以得到:度数× =弧度数,弧度数× =度数.一般情况下,省略弧度单位rad.
变式训练:将下列角度与弧度进行互化:
(2)- (3)10° (4)-855°
3.利用弧度表示角
例题:将-1 125°角写成α+2kπ(k∈Z)的形式,其中0≤α<2π,并判断它是第几象限角?
变式:若在本例的条件下,在[-4π,4π]范围内找出与α终边相同的角的集合.
注意:用弧度制表示终边相同的角的两个关注点
(1)用弧度制表示终边相同的角α+2kπ(k∈Z)时,其中2kπ是π的偶数倍,而不是整数倍.
(2)注意同一题目中角度制与弧度制不能混用.
变式训练:(1)用弧度制表示所有与75°角终边相同的角的集合是
(2)将手表的分针拨快10分钟,则分针在旋转过程中形成的角的弧度数是
4.弧度制下扇形的弧长与面积公式
思考:(1)我们初中所学扇形的弧长和面积公式是什么?
(2)扇形的弧长与面积公式(R是扇形所在圆的半径,n°为扇形的圆心角)
例题:已知扇形的周长为10 cm,面积为4 cm2,求扇形圆心角的弧度数.
变式训练:已知一扇形的周长为4,当它的半径与圆心角取何值时,扇形的面积最大?最大值是多少?
解题策略:(1)记公式:面积公式:S=lR=αR2,弧长公式:l=αR(其中l是扇形的弧长,R是扇形的半径,α是扇形圆心角的弧度数,0<α<2π).
涉及扇形的半径、周长、弧长、圆心角、面积等的计算问题,关键是分析题目中已知哪些量、要求哪些量,然后灵活运用弧长公式、扇形的面积公式直接求解或列方程(组)求解.变式训练 已知扇形的圆心角是α,半径为r,弧长为l.
变式训练:(1)若α=135°,r=10,求扇形的弧长l;
(2)若扇形AOB的周长为22,当扇形的圆心角α为多少弧度时,这个扇形的面积最大,并求出此时扇形的面积S的最大值.
小结:
1.知识清单:
(1)弧度制的概念.
(2)弧度与角度的相互转化.
(3)掌握特殊角的度数与弧度数的对应关系.
(4)扇形的弧长与面积的计算.
2.方法归纳:由特殊到一般、数学运算.
3.常见误区:弧度与角度易混用.
当堂测试
1.下列说法正确的是( )
A.1弧度的圆心角所对的弧长等于半径
B.大圆中1弧度的圆心角比小圆中1弧度的圆心角大
C.所有圆心角为1弧度的角所对的弧长都相等
D.用弧度表示的角都是正角
2.-660°等于( )
3.时钟的分针在1点到3点20分这段时间里转过的弧度为( )
4.已知一个扇形的弧长等于其所在圆半径的2倍,则该扇形圆心角的弧度数为 ,若该扇形的半径为1,则该扇形的面积为 .
5.已知角都是锐角,且角的终边与°角的终边相同,角的终边与670°角的终边相同,则______,______.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
