北师大版八年级上册 《数据的离散程度》教学课件第1课时(共29张PPT)
文档属性
| 名称 | 北师大版八年级上册 《数据的离散程度》教学课件第1课时(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 368.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 11:27:09 | ||
图片预览








文档简介
(共29张PPT)
6.4 数据的离散程度
第 1 课时
第六章 数据的分析
1.经历用方差刻画数据离散程度的过程,发展数据分析观念.
2.了解刻画数据离散程度的三个量——极差、方差和标准差,能借助计算器求出相应的数值,并在具体问题情景中加以应用.
学习目标
为了提高农副产品的国际竞争力,一些行业协会对农副产品的规格进行了划分,某外贸公司要出口一批规格为75 g的鸡腿.现有2个厂家提供货源,它们的价格相同,鸡腿的品质也相近.
质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿,它们的质量(单位:g)如下:
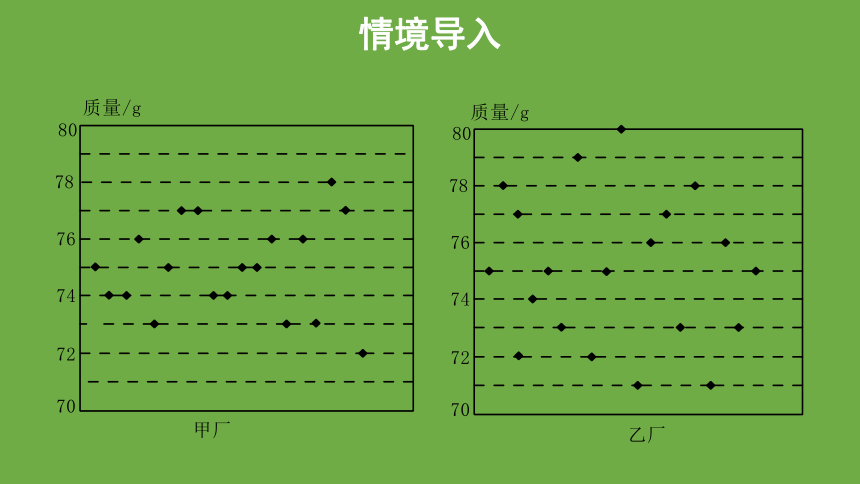
情境导入
甲厂:75 74 74 76 73 76 75 77 77 74 74 75 75 76 73 76 73 78 77 72
乙厂:75 78 72 77 74 75 73 79 72 75 80 71 76 77 73 78 71 76 73 75
把这些数据表示成下图:
情境导入
情境导入
(1)你能从图中估计出甲、乙两厂被抽取鸡腿的平均质量是多少?
(2)求甲、乙两厂被抽取鸡腿的平均质量,并在图中画出表示平均质量的直线.
(3)从甲厂抽取的这20只鸡腿质量的最大值是多少?最小值又是多少?它们相差几克?从乙厂抽取的这20只鸡腿质量的最大值又是多少?最小值呢?它们相差几克?
情境导入
75 g左右
都是75 g
甲厂:78 g,72 g,6 g;乙厂:80 g,71 g,9 g。
(4)如果只考虑鸡腿的规格,你认为外贸公司应购买哪家公司的鸡腿?说明你的理由.
极差是指一组数据中最大数据与最小数据的差.它是刻画数据离散程度的一个统计量.
情境导入
一般情况下,外贸公司应购买甲厂的鸡腿。
做一做:如果丙厂也参与了竞争,从该厂抽样调查了20只鸡腿,它们的质量数据如下图:
(1)丙厂这20只鸡腿质量的平均数和极差分别是多少?
(2)如何刻画丙厂这20只鸡腿的质量与其平均数的差距?分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距.
探究新知
平均数为75.1 g,极差为79-72=7 g.
可分别用这20只鸡腿的质量与其平均数的差的绝对值刻画.
(3)在甲、丙两厂中,你认为哪个厂的鸡腿质量更符合要求?为什么?
数学上,数据的离散程度还可以用方差或标准差刻画,方差是各个数据与平均数之差的平方的平均数,即:
探究新知
一般认为,甲厂的鸡腿质量更符合要求。这可以从统计图直观看出,也可以用上面所说的差距的和来说明。
注:
是这一组数据x1,x2,…,xn的平均数,s2是方差,而标准差就是方差的算术平方根.一般说来,一组数据的极差、方差、标准差越小,这组数据就越稳定.
说明:标准差的单位与已知数据的单位相同,使用时应当标明单位;方差的单位是已知单位的平方,使用时可以不标明单位.
探究新知
例 计算从甲厂抽取的20只鸡腿质量的方差.
解:甲厂20只鸡腿的平均质量:
甲厂20只鸡腿质量的方差:
探究新知
请自主探索用计算器求下列一组数据的标准差:
98 99 101 102 100 96 104 99 101 100
使用计算器探索求一组数据的标准差的具体操作步骤.(以CZ1206为例):
1.进入统计计算状态,按2ndf STAT ;
2.输入数据 然后按DATA ,显示的结果是输入数据的累计个数;
3.按 σ 即可直接得出结果.
自主探究
做一做:
1.分别计算从甲、丙两厂抽取的20只鸡腿质量的方差.
2.根据计算结果,你认为哪家的产品更符合规格要?
通过用计算器能计算出甲、丙两厂抽取的20只鸡腿的方差,得出方差较小的甲厂的产品更符合要求.
自主探究
例 据《生活报》报道,我省
有关部门要求各中小学要把
“每天锻炼一小时”写入课表.
为了响应这一号召,某校围绕着
“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
典例精讲
4
羽毛球
8
跳绳
10
足球
18
篮球
其他
最喜欢的体育活动项目的人数/人
最喜欢的体育活动项目
(1)该校对多少名学生
进行了抽样调查?
(2)本次抽样调查中,
5项人数的极差是多少?
典例精讲
解析:(1)由图1知4+8+10+18+10=50(名)
所以该校对50名学生进行了抽样调查.
(2)本次调查中,喜欢篮球活动的人数最多有 18人,喜欢羽毛球的人数最少有4人,所以极差是18-4=14(人).
典例精讲
课堂练习
1.刘翔在出征北京奥运会前刻苦进行110米跨栏训练,教练对他20次的训练成绩进行统计分析,判断他的成绩是否稳定,则教练需要知道刘翔这20次成绩的 ( )
A.众数 B.平均数 C.频数 D.方差
2.已知数据1,2,2,4,6,这组数据的方差是多少?
可先求出这组数据的平均数为
__,再根据方差计算公式
求出方差为____
D
3
3.2
3.数据0,1,2,4,3的 标准差为_____
4.某超市销售甲、乙两种饮料,七天的销售量如下表所示:
日期 15日 16日 17日 18日 19日 20日 21日
甲种饮料 48 57 62 60 59 45 46
乙种饮料 49 48 50 47 47 45 46
请你判断甲、乙 两种饮料哪一种销售比较稳定?
课堂练习
4.解:
因为
所以销售比价稳定的是甲种饮料
课堂练习
5.甲乙两支仪仗队队员的身高(单位:cm)如下:
甲队:178,177,179,179,178,178,177,178,177,179
乙队:178,177,179,176,178,180,180,178,176,178
哪支仪仗队更为整齐?你是怎么判断的?
课堂练习
课堂练习
分析:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为 ,则方差
它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
解:甲队的平均身高是:
(179×3+177×3+178×4)÷10=178(cm);
乙队的平均身高是:
(179+178×4+180×2+176×2+177)÷10=178(cm);
课堂练习
课堂练习
甲仪仗队更为整齐,理由如下:
S甲2= ×[3(177-178)2+4(178-178)2+3(179-178)2]=0.6;
S乙2= ×[2(176-178)2+(177-178)2+4(178-178)2+(179-178)2+2(180-178)2]=1.8;
∵0.6<1.8,
∴甲仪仗队更为整齐.
6. 甲乙二人参加某体育训练,近期5次测试成绩得分情况如下图所示:
分别求出两人得分的平均数与方差.
课堂练习
解析:此题数据较简单,由图容易看出:甲的五次成绩分别为:10分,13分,12分,14分,16分,乙的五次成绩依次为:13分,14分,12分,12分,14分. 容易求得二人平均成绩都是13分, ,
.从折线的走势就可看出甲的方差比乙的方差大.
课堂练习
7.为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早、中、晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志.数据汇总如下:
课堂练习
部分时段车流量情况调查表
时间 负责组别 车流总量 每分钟车流量
早晨上学 6:30~7:00 ①② 2747 92
中午放学 11:20~11:50 ③④ 1449 48
下午放学 5:00~5:30 ⑤⑥ 3669 122
回答下列问题:
(1)请你写出2条交通法规;
(2)早晨、中午、晚上三个时段每分钟车流量的极差是 ,这三个时段的车流总量的中位数是 ;
(3)观察表中的数据及统计图,写出你发现的一个现象并分析其原因;
(4)通过分析写一条合理化建议.
74
2747
课堂练习
通过本节课学习:
你知道了什么?
你发现了什么?
你学会了什么?
你想以后怎么样?
课堂小结
再见
6.4 数据的离散程度
第 1 课时
第六章 数据的分析
1.经历用方差刻画数据离散程度的过程,发展数据分析观念.
2.了解刻画数据离散程度的三个量——极差、方差和标准差,能借助计算器求出相应的数值,并在具体问题情景中加以应用.
学习目标
为了提高农副产品的国际竞争力,一些行业协会对农副产品的规格进行了划分,某外贸公司要出口一批规格为75 g的鸡腿.现有2个厂家提供货源,它们的价格相同,鸡腿的品质也相近.
质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿,它们的质量(单位:g)如下:
情境导入
甲厂:75 74 74 76 73 76 75 77 77 74 74 75 75 76 73 76 73 78 77 72
乙厂:75 78 72 77 74 75 73 79 72 75 80 71 76 77 73 78 71 76 73 75
把这些数据表示成下图:
情境导入
情境导入
(1)你能从图中估计出甲、乙两厂被抽取鸡腿的平均质量是多少?
(2)求甲、乙两厂被抽取鸡腿的平均质量,并在图中画出表示平均质量的直线.
(3)从甲厂抽取的这20只鸡腿质量的最大值是多少?最小值又是多少?它们相差几克?从乙厂抽取的这20只鸡腿质量的最大值又是多少?最小值呢?它们相差几克?
情境导入
75 g左右
都是75 g
甲厂:78 g,72 g,6 g;乙厂:80 g,71 g,9 g。
(4)如果只考虑鸡腿的规格,你认为外贸公司应购买哪家公司的鸡腿?说明你的理由.
极差是指一组数据中最大数据与最小数据的差.它是刻画数据离散程度的一个统计量.
情境导入
一般情况下,外贸公司应购买甲厂的鸡腿。
做一做:如果丙厂也参与了竞争,从该厂抽样调查了20只鸡腿,它们的质量数据如下图:
(1)丙厂这20只鸡腿质量的平均数和极差分别是多少?
(2)如何刻画丙厂这20只鸡腿的质量与其平均数的差距?分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距.
探究新知
平均数为75.1 g,极差为79-72=7 g.
可分别用这20只鸡腿的质量与其平均数的差的绝对值刻画.
(3)在甲、丙两厂中,你认为哪个厂的鸡腿质量更符合要求?为什么?
数学上,数据的离散程度还可以用方差或标准差刻画,方差是各个数据与平均数之差的平方的平均数,即:
探究新知
一般认为,甲厂的鸡腿质量更符合要求。这可以从统计图直观看出,也可以用上面所说的差距的和来说明。
注:
是这一组数据x1,x2,…,xn的平均数,s2是方差,而标准差就是方差的算术平方根.一般说来,一组数据的极差、方差、标准差越小,这组数据就越稳定.
说明:标准差的单位与已知数据的单位相同,使用时应当标明单位;方差的单位是已知单位的平方,使用时可以不标明单位.
探究新知
例 计算从甲厂抽取的20只鸡腿质量的方差.
解:甲厂20只鸡腿的平均质量:
甲厂20只鸡腿质量的方差:
探究新知
请自主探索用计算器求下列一组数据的标准差:
98 99 101 102 100 96 104 99 101 100
使用计算器探索求一组数据的标准差的具体操作步骤.(以CZ1206为例):
1.进入统计计算状态,按2ndf STAT ;
2.输入数据 然后按DATA ,显示的结果是输入数据的累计个数;
3.按 σ 即可直接得出结果.
自主探究
做一做:
1.分别计算从甲、丙两厂抽取的20只鸡腿质量的方差.
2.根据计算结果,你认为哪家的产品更符合规格要?
通过用计算器能计算出甲、丙两厂抽取的20只鸡腿的方差,得出方差较小的甲厂的产品更符合要求.
自主探究
例 据《生活报》报道,我省
有关部门要求各中小学要把
“每天锻炼一小时”写入课表.
为了响应这一号召,某校围绕着
“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
典例精讲
4
羽毛球
8
跳绳
10
足球
18
篮球
其他
最喜欢的体育活动项目的人数/人
最喜欢的体育活动项目
(1)该校对多少名学生
进行了抽样调查?
(2)本次抽样调查中,
5项人数的极差是多少?
典例精讲
解析:(1)由图1知4+8+10+18+10=50(名)
所以该校对50名学生进行了抽样调查.
(2)本次调查中,喜欢篮球活动的人数最多有 18人,喜欢羽毛球的人数最少有4人,所以极差是18-4=14(人).
典例精讲
课堂练习
1.刘翔在出征北京奥运会前刻苦进行110米跨栏训练,教练对他20次的训练成绩进行统计分析,判断他的成绩是否稳定,则教练需要知道刘翔这20次成绩的 ( )
A.众数 B.平均数 C.频数 D.方差
2.已知数据1,2,2,4,6,这组数据的方差是多少?
可先求出这组数据的平均数为
__,再根据方差计算公式
求出方差为____
D
3
3.2
3.数据0,1,2,4,3的 标准差为_____
4.某超市销售甲、乙两种饮料,七天的销售量如下表所示:
日期 15日 16日 17日 18日 19日 20日 21日
甲种饮料 48 57 62 60 59 45 46
乙种饮料 49 48 50 47 47 45 46
请你判断甲、乙 两种饮料哪一种销售比较稳定?
课堂练习
4.解:
因为
所以销售比价稳定的是甲种饮料
课堂练习
5.甲乙两支仪仗队队员的身高(单位:cm)如下:
甲队:178,177,179,179,178,178,177,178,177,179
乙队:178,177,179,176,178,180,180,178,176,178
哪支仪仗队更为整齐?你是怎么判断的?
课堂练习
课堂练习
分析:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为 ,则方差
它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
解:甲队的平均身高是:
(179×3+177×3+178×4)÷10=178(cm);
乙队的平均身高是:
(179+178×4+180×2+176×2+177)÷10=178(cm);
课堂练习
课堂练习
甲仪仗队更为整齐,理由如下:
S甲2= ×[3(177-178)2+4(178-178)2+3(179-178)2]=0.6;
S乙2= ×[2(176-178)2+(177-178)2+4(178-178)2+(179-178)2+2(180-178)2]=1.8;
∵0.6<1.8,
∴甲仪仗队更为整齐.
6. 甲乙二人参加某体育训练,近期5次测试成绩得分情况如下图所示:
分别求出两人得分的平均数与方差.
课堂练习
解析:此题数据较简单,由图容易看出:甲的五次成绩分别为:10分,13分,12分,14分,16分,乙的五次成绩依次为:13分,14分,12分,12分,14分. 容易求得二人平均成绩都是13分, ,
.从折线的走势就可看出甲的方差比乙的方差大.
课堂练习
7.为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早、中、晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志.数据汇总如下:
课堂练习
部分时段车流量情况调查表
时间 负责组别 车流总量 每分钟车流量
早晨上学 6:30~7:00 ①② 2747 92
中午放学 11:20~11:50 ③④ 1449 48
下午放学 5:00~5:30 ⑤⑥ 3669 122
回答下列问题:
(1)请你写出2条交通法规;
(2)早晨、中午、晚上三个时段每分钟车流量的极差是 ,这三个时段的车流总量的中位数是 ;
(3)观察表中的数据及统计图,写出你发现的一个现象并分析其原因;
(4)通过分析写一条合理化建议.
74
2747
课堂练习
通过本节课学习:
你知道了什么?
你发现了什么?
你学会了什么?
你想以后怎么样?
课堂小结
再见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
