2023-2024学年人教版九年级数学上册22.1.3(第1课时)二次函数y=ax2+k的图象和性质 课件(共21张PPT)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册22.1.3(第1课时)二次函数y=ax2+k的图象和性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 504.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第二十二章 二 次 函 数
二次函数y=ax2+k的图象和性质
教学目标:
【知识与技能】
1.能画出二次函数y=ax2+k的图象;
2.掌握二次函数y=ax2与y=ax2+k图象之间的联系;
3.掌握二次函数y=ax2+k的图象及其性质.
【过程与方法】
通过画二次函数y=2x2+1与y=2x2-1的图象,感受它们与y=2x2的联系,并由此得到y=ax2与y=ax2+k的图象及性质的联系和区别.
【情感态度与价值观】
在通过类比的方法获取二次函数y=ax2+k的图象及其性质过程中,进一步增强学生的数形结合意识,体会通过探究获得知识的乐趣.
教学重点:
1.二次函数y=ax2与y=ax2+k的图象之间的联系;
2.二次函数y=ax2+k的图象及其性质.
教学难点:
二次函数y=ax2+k的性质的基本应用.
1. 二次函数y=3x2的对称轴是______,顶点是_________,且当x=0时,函数y有最____值是______.
2. 抛物线y=-4x2在对称轴的右侧部分是______的(填“上升”或“下降”).
y轴
(0,0)
小
0
下降
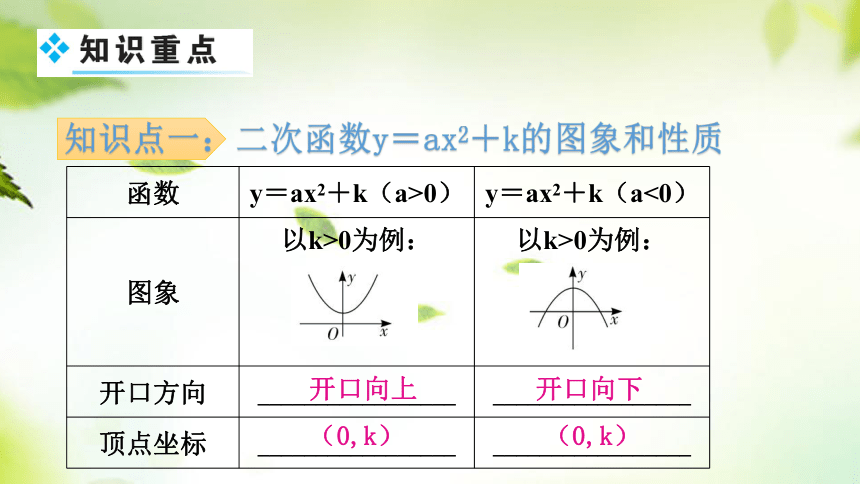
知识点一:二次函数y=ax2+k的图象和性质
函数 y=ax2+k(a>0) y=ax2+k(a<0)
图象 以k>0为例: 以k>0为例:
开口方向 _________________ _________________
顶点坐标 _________________ _________________
开口向上
开口向下
(0,k)
(0,k)
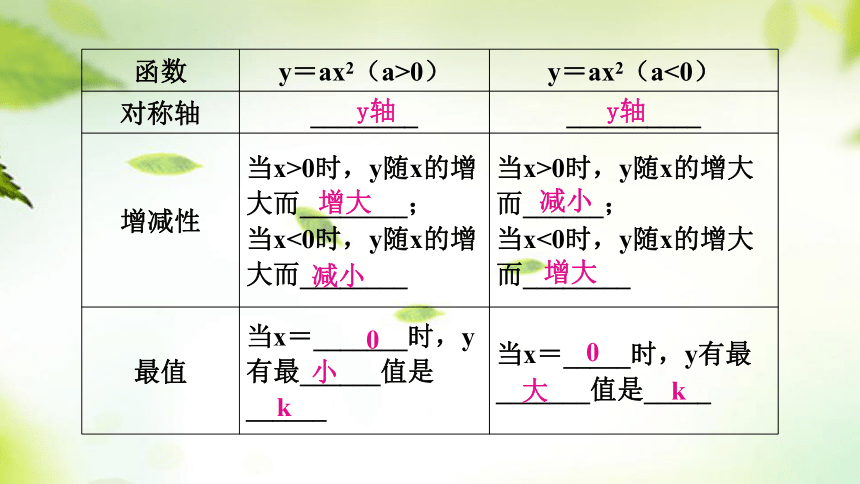
函数 y=ax2(a>0) y=ax2(a<0)
对称轴 ________ __________
增减性 当x>0时,y随x的增大而________; 当x<0时,y随x的增大而________ 当x>0时,y随x的增大而______;
当x<0时,y随x的增大而________
最值 当x=_______时,y有最______值是______ 当x=_____时,y有最_______值是_____
y轴
y轴
增大
减小
减小
增大
0
小
k
0
大
k
3. 函数y=3x2-5的开口向______,对称轴为直线x=______,顶点坐标为_________.
上
0
(0,-5)
4. 已知二次函数y=x2-5.
(1)当x<0时,y随x的增大而______;
(2)当x>0时,y随x的增大而______;
(3)当x=0时,y有最______值是______.
减小
增大
小
-5
图象形状相同,只是位置不同:当k>0时,由抛物线y=ax2向______平移______个单位长度得到y=ax2+k;当k<0时,由抛物线y=ax2向______平移______个单位长度得到y=ax2+k.
知识点二:二次函数y=ax2+k与y=ax2的关系
上
k
下
|k|
5. 将抛物线y=-x2向上平移1个单位长度得到抛物线__________________;将抛物线y=2x2向下平移9个单位长度得到抛物线______________.
y=-x2+1
y=2x2-9
【例1】抛物线y=-x2-1的图象大致是( )
思路点拨:由解析式中的a判断开口方向,k判断顶点坐标即可.
B
6. 抛物线y=x2+1的图象大致是( )
C
【例2】二次函数y=3x2-3的图象开口向_____,顶点坐标为__________,对称轴为______. 当x>0时,y随x的增大而______;当x<0时,y随x的增大而______. 因为a=3>0,所以y有最___值,当x=____时,y的最____值是______.
思路点拨:先由解析式知开口方向和顶点坐标,后画出草图,利用数形结合的方法分析解决问题,或根据二次函数y=ax2+k的图象性质直接作答.
上
(0,-3)
y轴
增大
减小
小
0
小
-3
7. 二次函数 y=-x2+7的图象是一条______线,它开口向____,对称轴是______,顶点坐标是_________.在对称轴左侧,y随x的增大而______;在对称轴右侧,y随x的增大而______;当x=______时,y的最______值是______.
抛物
下
y轴
(0,7)
增大
减小
0
大
7
【例3】(RJ九上P32例2改编)把y=-x2的图象向上平移2个单位长度.
(1)求新图象的解析式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后所得函数的最值,并求出x的对应值.
思路点拨:(1)根据平移规律“上加下减”写出平移后的抛物线解析式;
(2)根据抛物线解析式列函数对应值表,并作函数图象;
(3)结合函数图象回答问题.
(2)画图略.
解:(1)把y=-x2的图象向上平移2个单位长度后得到抛物线的解析式为y=-x2+2.
∴它的顶点坐标是(0,2),对称轴是直线x=0,
即y轴.
(3)由图象,得当x=0时,y最大值=2.
8. 如图22-13-1是抛物线y=x2在平面直角坐标系中的图象.
(1)将y=x2的图象向上平移2个
单位长度,画出平移后的图象;
(2)写出新图象的解析式、顶点坐标;
(3)求平移后所得函数的最值.
解:(1)画图略.
(2)由图象可知,新图象的解析式为y=x2+2,顶点坐标为(0,2).
(3)当x=0时,平移所得新函数有最小值,最小值为2.
本课小结:
师生共同回顾所学知识,如y=ax2+k的图象特征,函数的增减性等,并对可能出现的困难、疑问给予整理,进行辨析.
教学反思:
本课时教学重点在于培养学生的比较能力,旨在希望学生通过对比发现函数图象的性质,从而进一步增强学生的数形结合意识,体会通过探究获得知识的乐趣.
谢 谢
第二十二章 二 次 函 数
二次函数y=ax2+k的图象和性质
教学目标:
【知识与技能】
1.能画出二次函数y=ax2+k的图象;
2.掌握二次函数y=ax2与y=ax2+k图象之间的联系;
3.掌握二次函数y=ax2+k的图象及其性质.
【过程与方法】
通过画二次函数y=2x2+1与y=2x2-1的图象,感受它们与y=2x2的联系,并由此得到y=ax2与y=ax2+k的图象及性质的联系和区别.
【情感态度与价值观】
在通过类比的方法获取二次函数y=ax2+k的图象及其性质过程中,进一步增强学生的数形结合意识,体会通过探究获得知识的乐趣.
教学重点:
1.二次函数y=ax2与y=ax2+k的图象之间的联系;
2.二次函数y=ax2+k的图象及其性质.
教学难点:
二次函数y=ax2+k的性质的基本应用.
1. 二次函数y=3x2的对称轴是______,顶点是_________,且当x=0时,函数y有最____值是______.
2. 抛物线y=-4x2在对称轴的右侧部分是______的(填“上升”或“下降”).
y轴
(0,0)
小
0
下降
知识点一:二次函数y=ax2+k的图象和性质
函数 y=ax2+k(a>0) y=ax2+k(a<0)
图象 以k>0为例: 以k>0为例:
开口方向 _________________ _________________
顶点坐标 _________________ _________________
开口向上
开口向下
(0,k)
(0,k)
函数 y=ax2(a>0) y=ax2(a<0)
对称轴 ________ __________
增减性 当x>0时,y随x的增大而________; 当x<0时,y随x的增大而________ 当x>0时,y随x的增大而______;
当x<0时,y随x的增大而________
最值 当x=_______时,y有最______值是______ 当x=_____时,y有最_______值是_____
y轴
y轴
增大
减小
减小
增大
0
小
k
0
大
k
3. 函数y=3x2-5的开口向______,对称轴为直线x=______,顶点坐标为_________.
上
0
(0,-5)
4. 已知二次函数y=x2-5.
(1)当x<0时,y随x的增大而______;
(2)当x>0时,y随x的增大而______;
(3)当x=0时,y有最______值是______.
减小
增大
小
-5
图象形状相同,只是位置不同:当k>0时,由抛物线y=ax2向______平移______个单位长度得到y=ax2+k;当k<0时,由抛物线y=ax2向______平移______个单位长度得到y=ax2+k.
知识点二:二次函数y=ax2+k与y=ax2的关系
上
k
下
|k|
5. 将抛物线y=-x2向上平移1个单位长度得到抛物线__________________;将抛物线y=2x2向下平移9个单位长度得到抛物线______________.
y=-x2+1
y=2x2-9
【例1】抛物线y=-x2-1的图象大致是( )
思路点拨:由解析式中的a判断开口方向,k判断顶点坐标即可.
B
6. 抛物线y=x2+1的图象大致是( )
C
【例2】二次函数y=3x2-3的图象开口向_____,顶点坐标为__________,对称轴为______. 当x>0时,y随x的增大而______;当x<0时,y随x的增大而______. 因为a=3>0,所以y有最___值,当x=____时,y的最____值是______.
思路点拨:先由解析式知开口方向和顶点坐标,后画出草图,利用数形结合的方法分析解决问题,或根据二次函数y=ax2+k的图象性质直接作答.
上
(0,-3)
y轴
增大
减小
小
0
小
-3
7. 二次函数 y=-x2+7的图象是一条______线,它开口向____,对称轴是______,顶点坐标是_________.在对称轴左侧,y随x的增大而______;在对称轴右侧,y随x的增大而______;当x=______时,y的最______值是______.
抛物
下
y轴
(0,7)
增大
减小
0
大
7
【例3】(RJ九上P32例2改编)把y=-x2的图象向上平移2个单位长度.
(1)求新图象的解析式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后所得函数的最值,并求出x的对应值.
思路点拨:(1)根据平移规律“上加下减”写出平移后的抛物线解析式;
(2)根据抛物线解析式列函数对应值表,并作函数图象;
(3)结合函数图象回答问题.
(2)画图略.
解:(1)把y=-x2的图象向上平移2个单位长度后得到抛物线的解析式为y=-x2+2.
∴它的顶点坐标是(0,2),对称轴是直线x=0,
即y轴.
(3)由图象,得当x=0时,y最大值=2.
8. 如图22-13-1是抛物线y=x2在平面直角坐标系中的图象.
(1)将y=x2的图象向上平移2个
单位长度,画出平移后的图象;
(2)写出新图象的解析式、顶点坐标;
(3)求平移后所得函数的最值.
解:(1)画图略.
(2)由图象可知,新图象的解析式为y=x2+2,顶点坐标为(0,2).
(3)当x=0时,平移所得新函数有最小值,最小值为2.
本课小结:
师生共同回顾所学知识,如y=ax2+k的图象特征,函数的增减性等,并对可能出现的困难、疑问给予整理,进行辨析.
教学反思:
本课时教学重点在于培养学生的比较能力,旨在希望学生通过对比发现函数图象的性质,从而进一步增强学生的数形结合意识,体会通过探究获得知识的乐趣.
谢 谢
同课章节目录
