贵州省铜仁市2022-2023学年高二下学期7月期末质量监测试数学试题(Word版含答案)
文档属性
| 名称 | 贵州省铜仁市2022-2023学年高二下学期7月期末质量监测试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 750.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 13:31:13 | ||
图片预览



文档简介
铜仁市2022-2023学年高二下学期7月期末质量监测试
数 学
本试卷共4页,22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
2.答案全部填写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第I部分 选择题(共60分)
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.复数对应的点在复平面内的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.函数的图象与函数的图象关于轴对称,则( )
A. B. C.4 D.
4.音程由两个音组成,是和声的最小单位.有的音听起来和谐而有的则不和谐,这和音与音之间的波形(正弦型)有关.比如,1(do)到i(高音do)可以构成纯八度音程,听感上十分和谐,这是因为两者波形的周期比为,两个声波在1个(2个)周期后就立即重合,并有规律的进行下去.再比如1(do)到5(sol)可以构成纯五度音程,两者周期比为3:2,两个声波在2个(3个)周期后就立即重合,听感上也很和谐.也就是说,两个音波形的周期比例越简单,听感越和谐.已知在一个调性中,1(do)的波形符合函数(为振幅,为时间),在音与音之间振幅相同的情况下,与1(do)构成纯八度音程的i(高音do)、纯五度音程的5(sol)的波形函数分别为( )
A.; B.;
C.; D.;
5.已知双曲线的渐近线方程为,则的值为( )
A.9 B. C.3 D.
6.点在圆:上运动,点,当直线的斜率最大时,直线方程是( )
A. B.
C. D.
7.已知是腰长为2的等腰直角斜边上的动点,则的取值范围是( )
A. B. C. D.
8.已知函数,若存在,使得,则实数的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下图是国家卫健委给出的全国某种流行病通报中,甲、乙两个省2月份从2月7日到2月13日一周新增该种流行病确诊人数的折线图:( )
A.甲省方差比乙省方差大 B.甲省平均数比乙省平均数大
C.甲省中位数比乙省中位数大 D.甲省的极差比乙省极差大
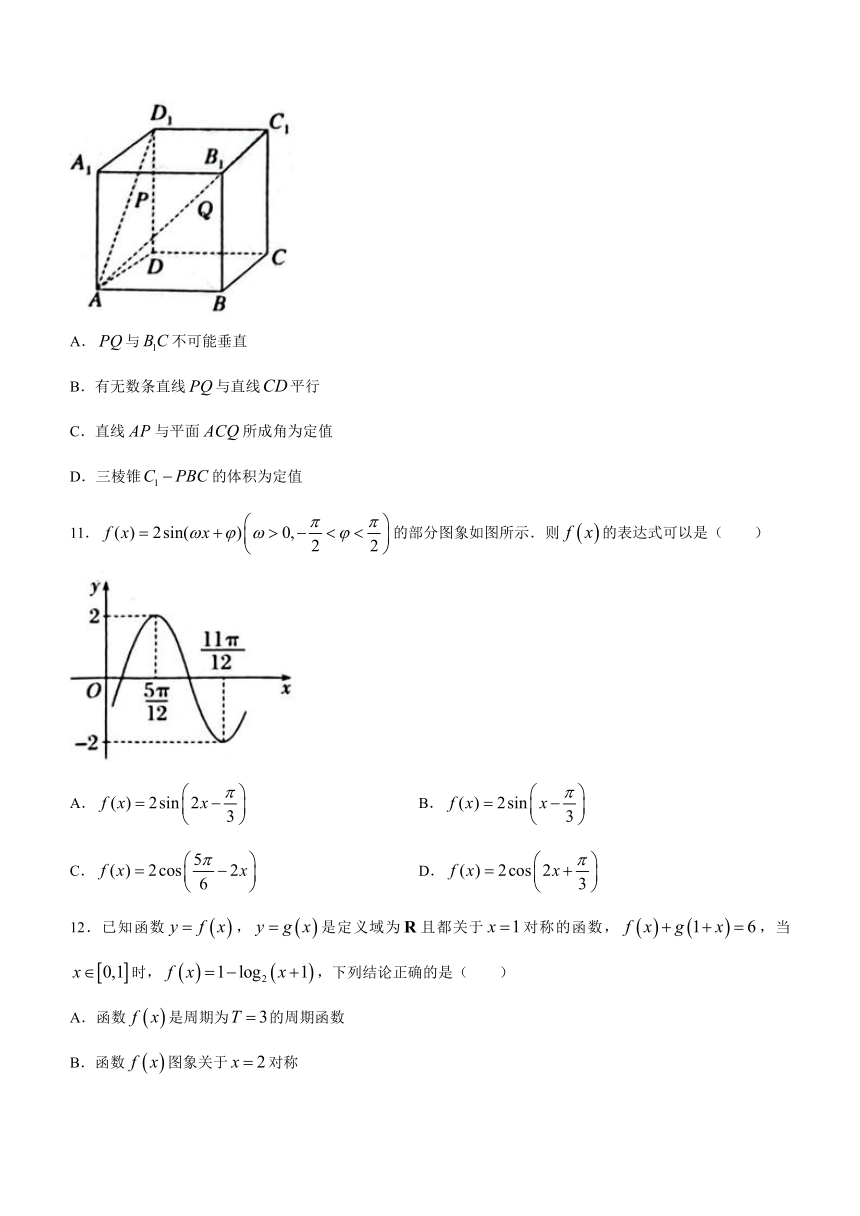
10.在正方体中,棱长为1,已知点,分别是线段,上的动点(不含端点).下列结论正确的选项是( )
A.与不可能垂直
B.有无数条直线与直线平行
C.直线与平面所成角为定值
D.三棱锥的体积为定值
11.的部分图象如图所示.则的表达式可以是( )
A. B.
C. D.
12.已知函数,是定义域为且都关于对称的函数,,当时,,下列结论正确的是( )
A.函数是周期为的周期函数
B.函数图象关于对称
C.
D.的图象与的图象有8个交点
第II部分 非选择题(共90分)
三、填空题:本大题共4小题,每小题5分,满分20分.
13.准线方程为的抛物线的标准方程是________________.
14.在的展开式中,项的系数为________.(用数字作答)
15.请举出一个各项均为正数且公差不为0的等差数列,使得它的前项和满足:数列也是等差数列,则________.
16.粽子是端午节期间不可缺少的传统美食,铜仁的粽子不仅馅料丰富多样,形状也是五花八门,有竹筒形、长方体形、圆锥形等,但最常见的还是“四角粽子”,其外形近似于正三棱锥.因为将粽子包成这样形状,既可以节约原料,又不失饱满,而且十分美观.如图,假设一个粽子的外形是正三棱锥,其侧棱和底面边长分别是8cm和6cm,是顶点在底面上的射影.若是底面内的动点,且直线与底面所成角的正切值为,则动点的轨迹长为________.
四、解答题:本大题共6小题,满分70分.解答应写出文字说明、演算步骤或证明.
17.(本小题满分10分)
在中,,,.
(1)求;
(2)若为的中点,求的长.
18.(本小题满分12分)
来自微碧江的报道:2023年6月17日,铜仁市碧江区第二届房地产交易展示会在三江公园隆重开幕.据了解,本次房交会以政府搭台、企业让利、政策支持、百姓受益为办展宗旨,聚集了碧江区17家房开企业、18个楼盘参展,2080套房源、25万平方米供群众选购,9大银行和公积金中心在现场助阵和提供咨询服务.本次房交会从6月17日持续到6月22日,期间每天都安排有精彩演出、免费美食、互动游戏、露天电影和游江龙舟五类活动.
(1)甲、乙两名市民参加了不同类的活动,且每人只参加一类活动.已知甲参加了免费美食的活动,求乙参加游江龙舟活动的概率是多少
(2)已知来自某小区的市民参加互动游戏的概率是,设来自该小区的2名市民参加互动游戏的人数为,求的分布列与期望.
19.(本小题满分12分)
已知数列满足,.
(1)求证:数列是等比数列;
(2)求数列的通项公式及它的前项和.
20.(本小题满分12分)
如图,在三棱柱中,底面是等边三角形,.
(1)证明:;
(2)若平面平面,且,求直线与平面所成角的正弦值.
21.(本小题满分12分)
已知椭圆:的离心率为,且过点.
(1)求的方程;
(2)直线:与椭圆分别相交于,两点,且,点不在直线上:
(I)试证明直线过一定点,并求出此定点;
(II)从点作垂足为,点,写出的最小值(结论不要求证明).
22.(本小题满分12分)
已知函数.
(1)当时,
(I)求处的切线方程;
(II)判断的单调性,并给出证明;
(2)若恒成立,求的取值范围.
铜仁市2022-2023学年高二下学期7月期末质量监测试
数学答案
第一部分(选择题 共60分)
一、选择题(12小题,共60分)
1 2 3 4 5 6 7 8 9 10 11 12
C A D A A C C B ACD BCD AC BC
第二部分(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,满分20分.)
13.
14.
15.(答案不唯一)
16.
三、解答题(本大题共6小题,满分70分.解答应写出文字说明、演算步骤或证明.)
17.解:(1)在中,由正弦定理,
得:;
(2) 由(1)得,,在中,由余弦定理得:
,可得:.
18.解:(1)在甲参加了免费美食活动的条件下,记“乙参加游江龙舟活动的这一事件”为,则.
(2)可取0,1,2,
;;.
0 1 2
19.解:(1)证明: ,,
又a1+1=3,所以数列{an+n}是以3为首项,3为公比的等比数列.
(2)设,,由(1)得:,可得:,可得:
20.解:(1)证明:设为AB的中点,连接,由题意得:,,
,所以平面,可得.
(2) 因为平面平面,由平面垂直性质得:,
所以两两垂直,建立如图所示的坐标系,
,
则,,
,设平面的法向量为,
则,设直线与平面所成角为,
则.
21. 解:(1),,得,的方程:.
(2)(ⅰ)设,,,
由根与系数的关系得:,,,由, =0
得:,代入整理得:,分解得:,点不在直线上
所以,可得,直线过定点.
()的最小值为.
22.解:(1)当a=1时,f(x)=x2-x sin x+1,可得:f′(x)=2x-sin x-xcos x.
(ⅰ)f(π)=π2+1,f′(π)=3π,可得:y=3πx-2π2+1.
(ⅱ)f′(x)=2x-sin x-x cos x=x-sin x+x(1-cos x),
设m(x)=x-sin x(x>0) m′(x)=1-cos x≥0,m(x)单调递增,m(x)>m(0)=0 x>sin x可得:f′(x)>0,f(x)单调递增.
(2)设g(x)=f(x)-1=ax2-a(xsin x+cos x)+cos x+a-1,由题意恒成立.
①当时,=不恒成立,不合题意;
②当时, 设,,,,,设
r(x)=h′(x),,单调递增,由零点存在定理得,在上,,在上单调递减,g(x)③当时, ,
可得:,所以,.
注:第一问亦可将函数分开进行讨论,确定单调性.
数 学
本试卷共4页,22题。全卷满分150分。考试用时120分钟。
注意事项:
1.答题前,考生务必将自己的姓名、准考证号填写在本试卷相应的位置。
2.答案全部填写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第I部分 选择题(共60分)
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.复数对应的点在复平面内的( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.函数的图象与函数的图象关于轴对称,则( )
A. B. C.4 D.
4.音程由两个音组成,是和声的最小单位.有的音听起来和谐而有的则不和谐,这和音与音之间的波形(正弦型)有关.比如,1(do)到i(高音do)可以构成纯八度音程,听感上十分和谐,这是因为两者波形的周期比为,两个声波在1个(2个)周期后就立即重合,并有规律的进行下去.再比如1(do)到5(sol)可以构成纯五度音程,两者周期比为3:2,两个声波在2个(3个)周期后就立即重合,听感上也很和谐.也就是说,两个音波形的周期比例越简单,听感越和谐.已知在一个调性中,1(do)的波形符合函数(为振幅,为时间),在音与音之间振幅相同的情况下,与1(do)构成纯八度音程的i(高音do)、纯五度音程的5(sol)的波形函数分别为( )
A.; B.;
C.; D.;
5.已知双曲线的渐近线方程为,则的值为( )
A.9 B. C.3 D.
6.点在圆:上运动,点,当直线的斜率最大时,直线方程是( )
A. B.
C. D.
7.已知是腰长为2的等腰直角斜边上的动点,则的取值范围是( )
A. B. C. D.
8.已知函数,若存在,使得,则实数的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下图是国家卫健委给出的全国某种流行病通报中,甲、乙两个省2月份从2月7日到2月13日一周新增该种流行病确诊人数的折线图:( )
A.甲省方差比乙省方差大 B.甲省平均数比乙省平均数大
C.甲省中位数比乙省中位数大 D.甲省的极差比乙省极差大
10.在正方体中,棱长为1,已知点,分别是线段,上的动点(不含端点).下列结论正确的选项是( )
A.与不可能垂直
B.有无数条直线与直线平行
C.直线与平面所成角为定值
D.三棱锥的体积为定值
11.的部分图象如图所示.则的表达式可以是( )
A. B.
C. D.
12.已知函数,是定义域为且都关于对称的函数,,当时,,下列结论正确的是( )
A.函数是周期为的周期函数
B.函数图象关于对称
C.
D.的图象与的图象有8个交点
第II部分 非选择题(共90分)
三、填空题:本大题共4小题,每小题5分,满分20分.
13.准线方程为的抛物线的标准方程是________________.
14.在的展开式中,项的系数为________.(用数字作答)
15.请举出一个各项均为正数且公差不为0的等差数列,使得它的前项和满足:数列也是等差数列,则________.
16.粽子是端午节期间不可缺少的传统美食,铜仁的粽子不仅馅料丰富多样,形状也是五花八门,有竹筒形、长方体形、圆锥形等,但最常见的还是“四角粽子”,其外形近似于正三棱锥.因为将粽子包成这样形状,既可以节约原料,又不失饱满,而且十分美观.如图,假设一个粽子的外形是正三棱锥,其侧棱和底面边长分别是8cm和6cm,是顶点在底面上的射影.若是底面内的动点,且直线与底面所成角的正切值为,则动点的轨迹长为________.
四、解答题:本大题共6小题,满分70分.解答应写出文字说明、演算步骤或证明.
17.(本小题满分10分)
在中,,,.
(1)求;
(2)若为的中点,求的长.
18.(本小题满分12分)
来自微碧江的报道:2023年6月17日,铜仁市碧江区第二届房地产交易展示会在三江公园隆重开幕.据了解,本次房交会以政府搭台、企业让利、政策支持、百姓受益为办展宗旨,聚集了碧江区17家房开企业、18个楼盘参展,2080套房源、25万平方米供群众选购,9大银行和公积金中心在现场助阵和提供咨询服务.本次房交会从6月17日持续到6月22日,期间每天都安排有精彩演出、免费美食、互动游戏、露天电影和游江龙舟五类活动.
(1)甲、乙两名市民参加了不同类的活动,且每人只参加一类活动.已知甲参加了免费美食的活动,求乙参加游江龙舟活动的概率是多少
(2)已知来自某小区的市民参加互动游戏的概率是,设来自该小区的2名市民参加互动游戏的人数为,求的分布列与期望.
19.(本小题满分12分)
已知数列满足,.
(1)求证:数列是等比数列;
(2)求数列的通项公式及它的前项和.
20.(本小题满分12分)
如图,在三棱柱中,底面是等边三角形,.
(1)证明:;
(2)若平面平面,且,求直线与平面所成角的正弦值.
21.(本小题满分12分)
已知椭圆:的离心率为,且过点.
(1)求的方程;
(2)直线:与椭圆分别相交于,两点,且,点不在直线上:
(I)试证明直线过一定点,并求出此定点;
(II)从点作垂足为,点,写出的最小值(结论不要求证明).
22.(本小题满分12分)
已知函数.
(1)当时,
(I)求处的切线方程;
(II)判断的单调性,并给出证明;
(2)若恒成立,求的取值范围.
铜仁市2022-2023学年高二下学期7月期末质量监测试
数学答案
第一部分(选择题 共60分)
一、选择题(12小题,共60分)
1 2 3 4 5 6 7 8 9 10 11 12
C A D A A C C B ACD BCD AC BC
第二部分(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,满分20分.)
13.
14.
15.(答案不唯一)
16.
三、解答题(本大题共6小题,满分70分.解答应写出文字说明、演算步骤或证明.)
17.解:(1)在中,由正弦定理,
得:;
(2) 由(1)得,,在中,由余弦定理得:
,可得:.
18.解:(1)在甲参加了免费美食活动的条件下,记“乙参加游江龙舟活动的这一事件”为,则.
(2)可取0,1,2,
;;.
0 1 2
19.解:(1)证明: ,,
又a1+1=3,所以数列{an+n}是以3为首项,3为公比的等比数列.
(2)设,,由(1)得:,可得:,可得:
20.解:(1)证明:设为AB的中点,连接,由题意得:,,
,所以平面,可得.
(2) 因为平面平面,由平面垂直性质得:,
所以两两垂直,建立如图所示的坐标系,
,
则,,
,设平面的法向量为,
则,设直线与平面所成角为,
则.
21. 解:(1),,得,的方程:.
(2)(ⅰ)设,,,
由根与系数的关系得:,,,由, =0
得:,代入整理得:,分解得:,点不在直线上
所以,可得,直线过定点.
()的最小值为.
22.解:(1)当a=1时,f(x)=x2-x sin x+1,可得:f′(x)=2x-sin x-xcos x.
(ⅰ)f(π)=π2+1,f′(π)=3π,可得:y=3πx-2π2+1.
(ⅱ)f′(x)=2x-sin x-x cos x=x-sin x+x(1-cos x),
设m(x)=x-sin x(x>0) m′(x)=1-cos x≥0,m(x)单调递增,m(x)>m(0)=0 x>sin x可得:f′(x)>0,f(x)单调递增.
(2)设g(x)=f(x)-1=ax2-a(xsin x+cos x)+cos x+a-1,由题意恒成立.
①当时,=不恒成立,不合题意;
②当时, 设,,,,,设
r(x)=h′(x),,单调递增,由零点存在定理得,在上,,在上单调递减,g(x)
可得:,所以,.
注:第一问亦可将函数分开进行讨论,确定单调性.
同课章节目录
