九年级数学上册试题 第22章《相似形》单元测试-沪科版(含答案)
文档属性
| 名称 | 九年级数学上册试题 第22章《相似形》单元测试-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 987.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 20:38:25 | ||
图片预览




文档简介
第22章《相似形》单元测试
一、选择题(本大题共10小题,每小题3分,共30分).
1.观察下列图形中,是相似图形的一组是
A. B.
C. D.
2.在一幅比例尺是的地图上,量得上海到杭州的距离是.那么上海到杭州的实际距离是
A. B. C. D.
3.下面四组线段中,成比例的是
A.,,, B.,,,
C.,,, D.,,,
4.如图,在中,,且,则的值为
A. B. C. D.
5.如图,在中,,,若的周长为,则的周长是
A. B. C. D.
6.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么较短线段的长度为
A. B. C. D.
7.如图,在平行四边形中,点是上一点,,连接交于点,延长交的延长线于点,则的值为
A. B. C. D.
8.在中,点、分别在边、的延长线上,下列比例式中能判定的为
A. B. C. D.
9.如图,在中,点在边上,,,联结,与相交于点,则下列结论一定正确的是
A. B. C. D.
10.如图,已知在中,点、点是边上的两点,联结、,且,如果,那么下列等式错误的是
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知两个三角形是相似形,其中一个三角形的两个角分别为、,则另一个三角形的最大内角的度数为 .
12.若线段,,则线段,的比例中项为 .
13.一把剪刀如图所示,,,当手握的地方张开时,剪刀的尖端,两点的距离为 .
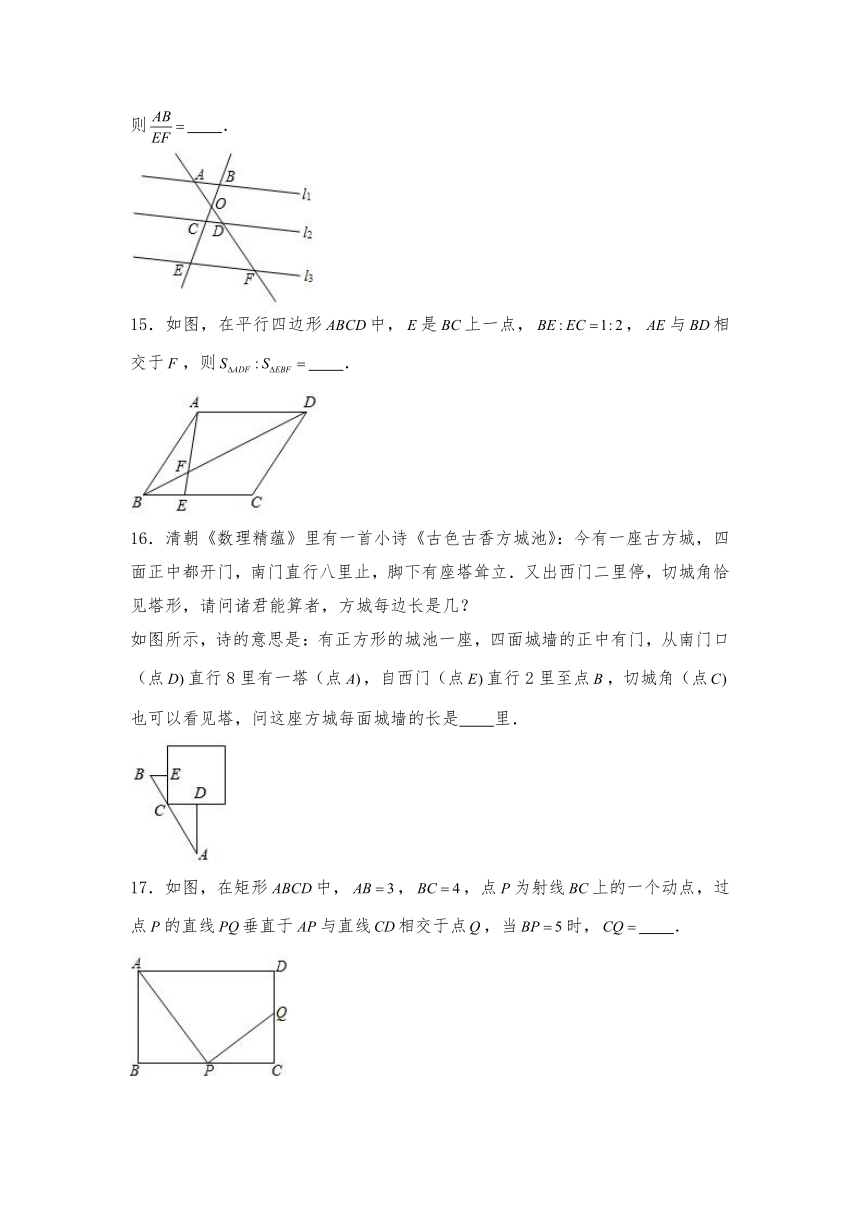
14.如图,直线,直线分别交,,于点,,,直线分别交,,于点,,,两直线,相交于点.若,,则 .
15.如图,在平行四边形中,是上一点,,与相交于,则 .
16.清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?
如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点直行8里有一塔(点,自西门(点直行2里至点,切城角(点也可以看见塔,问这座方城每面城墙的长是 里.
17.如图,在矩形中,,,点为射线上的一个动点,过点的直线垂直于与直线相交于点,当时, .
18.如图,在矩形中,,,点是上的动点(不与端点重合),在矩形内找点,使得,且满足,则线段的最小值是 .
三、解答题(本大题共8小题,共66分.)
19.已知线段是,的比例中项,,,求的长.
20.(1)化简:;
(2)如图,,直线,与,,分别相交于点,,和点,,.若,,,求的长.
21.如图,已知,,,,.
(1)求的长;
(2)求的长.
22.如图,是的边的中点,,,与相交于,求证:是的中点.
23.如图,点、是的边上的两点,满足,联结,过点作,交边于,联结.
(1)求证:;
(2)的面积为3,的面积为2,求的面积.
24.如图,已知在中,,平分,交边于点,是边上一点,且,过点作,分别交、于点、,联结.
(1)求证:四边形是菱形;
(2)求证:.
25.已知:如图,在中,,垂足为点,,点为边上一点,且,联结并延长,交边于点.
(1)求证:;
(2)过点作的平行线交的延长线于点,联结.如果,求证:四边形是矩形.
26.如图,已知在中,,平分,交边于点,是边上一点,且,过点作,分别交、于点、,联结.
(1)求证:四边形是菱形;
(2)求证:;
(3)若,,联结,求的值.
答案
一、选择题
..........
二.填空题
11.. 12.6. 13.6. 14.. 15.9.
16.8. 17.. 18.2.
三.解答题
19.线段是,的比例中项,
,
,
,
,,
.
20.(1)原式
;
(2),
,即,
解得.
21.(1),
,即,
解得,,
则;
(2),
,即,
解得,.
22.证明:是的边的中点,
,
,
,
,
,
,
,即是的中点.
23.(1)证明:,
,
,
,
,
;
(2)解:,的面积为3,的面积为2,
,,
,
即,
解得:的面积.
24.(1)证明:
平分,
.
,,
.
.
同理可得.
,.
,
.
.
.
.
四边形是菱形.
(2)证明:由(1)得,
.
四边形是菱形,
.
.
.
,
.
,
即.
25.(1)证明:,
,
在和中,
,
,
,
又,
,
,
即;
(2)证明:,
,
由(1)知,
,
又,
,
,
,
,,
,
,
又,
四边形是平行四边形,
,
四边形是矩形(有一个角是直角的平行四边形是矩形).
26.(1)证明:如图,
平分,
,
,,
,
,
同理可得,
,,
,
,
,
,
,
四边形是菱形.
(2)证明:由(1)得,
,
四边形是菱形,
,
,
,
,
,
,即.
(3)由(2)得,,,
,
,
,
,
,
,
,
,
,
,
,
,
,,,
,
点是的黄金分割点,
,
,
,
,
,
.
一、选择题(本大题共10小题,每小题3分,共30分).
1.观察下列图形中,是相似图形的一组是
A. B.
C. D.
2.在一幅比例尺是的地图上,量得上海到杭州的距离是.那么上海到杭州的实际距离是
A. B. C. D.
3.下面四组线段中,成比例的是
A.,,, B.,,,
C.,,, D.,,,
4.如图,在中,,且,则的值为
A. B. C. D.
5.如图,在中,,,若的周长为,则的周长是
A. B. C. D.
6.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,为的黄金分割点,如果的长度为,那么较短线段的长度为
A. B. C. D.
7.如图,在平行四边形中,点是上一点,,连接交于点,延长交的延长线于点,则的值为
A. B. C. D.
8.在中,点、分别在边、的延长线上,下列比例式中能判定的为
A. B. C. D.
9.如图,在中,点在边上,,,联结,与相交于点,则下列结论一定正确的是
A. B. C. D.
10.如图,已知在中,点、点是边上的两点,联结、,且,如果,那么下列等式错误的是
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知两个三角形是相似形,其中一个三角形的两个角分别为、,则另一个三角形的最大内角的度数为 .
12.若线段,,则线段,的比例中项为 .
13.一把剪刀如图所示,,,当手握的地方张开时,剪刀的尖端,两点的距离为 .
14.如图,直线,直线分别交,,于点,,,直线分别交,,于点,,,两直线,相交于点.若,,则 .
15.如图,在平行四边形中,是上一点,,与相交于,则 .
16.清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?
如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点直行8里有一塔(点,自西门(点直行2里至点,切城角(点也可以看见塔,问这座方城每面城墙的长是 里.
17.如图,在矩形中,,,点为射线上的一个动点,过点的直线垂直于与直线相交于点,当时, .
18.如图,在矩形中,,,点是上的动点(不与端点重合),在矩形内找点,使得,且满足,则线段的最小值是 .
三、解答题(本大题共8小题,共66分.)
19.已知线段是,的比例中项,,,求的长.
20.(1)化简:;
(2)如图,,直线,与,,分别相交于点,,和点,,.若,,,求的长.
21.如图,已知,,,,.
(1)求的长;
(2)求的长.
22.如图,是的边的中点,,,与相交于,求证:是的中点.
23.如图,点、是的边上的两点,满足,联结,过点作,交边于,联结.
(1)求证:;
(2)的面积为3,的面积为2,求的面积.
24.如图,已知在中,,平分,交边于点,是边上一点,且,过点作,分别交、于点、,联结.
(1)求证:四边形是菱形;
(2)求证:.
25.已知:如图,在中,,垂足为点,,点为边上一点,且,联结并延长,交边于点.
(1)求证:;
(2)过点作的平行线交的延长线于点,联结.如果,求证:四边形是矩形.
26.如图,已知在中,,平分,交边于点,是边上一点,且,过点作,分别交、于点、,联结.
(1)求证:四边形是菱形;
(2)求证:;
(3)若,,联结,求的值.
答案
一、选择题
..........
二.填空题
11.. 12.6. 13.6. 14.. 15.9.
16.8. 17.. 18.2.
三.解答题
19.线段是,的比例中项,
,
,
,
,,
.
20.(1)原式
;
(2),
,即,
解得.
21.(1),
,即,
解得,,
则;
(2),
,即,
解得,.
22.证明:是的边的中点,
,
,
,
,
,
,
,即是的中点.
23.(1)证明:,
,
,
,
,
;
(2)解:,的面积为3,的面积为2,
,,
,
即,
解得:的面积.
24.(1)证明:
平分,
.
,,
.
.
同理可得.
,.
,
.
.
.
.
四边形是菱形.
(2)证明:由(1)得,
.
四边形是菱形,
.
.
.
,
.
,
即.
25.(1)证明:,
,
在和中,
,
,
,
又,
,
,
即;
(2)证明:,
,
由(1)知,
,
又,
,
,
,
,,
,
,
又,
四边形是平行四边形,
,
四边形是矩形(有一个角是直角的平行四边形是矩形).
26.(1)证明:如图,
平分,
,
,,
,
,
同理可得,
,,
,
,
,
,
,
四边形是菱形.
(2)证明:由(1)得,
,
四边形是菱形,
,
,
,
,
,
,即.
(3)由(2)得,,,
,
,
,
,
,
,
,
,
,
,
,
,
,,,
,
点是的黄金分割点,
,
,
,
,
,
.
