九年级数学上册试题 21.4二次函数的应用:抛物型问题 -沪科版(含答案)
文档属性
| 名称 | 九年级数学上册试题 21.4二次函数的应用:抛物型问题 -沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 271.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 22:28:37 | ||
图片预览



文档简介
21.4二次函数的应用:抛物型问题
一、选择题
1.在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为yx2x,由此可知小宇此次实心球训练的成绩为( )
A.米 B.8米 C.10米 D.2米
2.以固定的初速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量为( )
A.﹣4.9和v0 B.v0和t C.t D.h
3.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+3,则下列结论错误的是( )
A.柱子OA的高度为3m
B.喷出的水流距柱子1m处达到最大高度
C.喷出的水流距水平面的最大高度是3m
D.水池的半径至少要3m才能使喷出的水流不至于落在池外
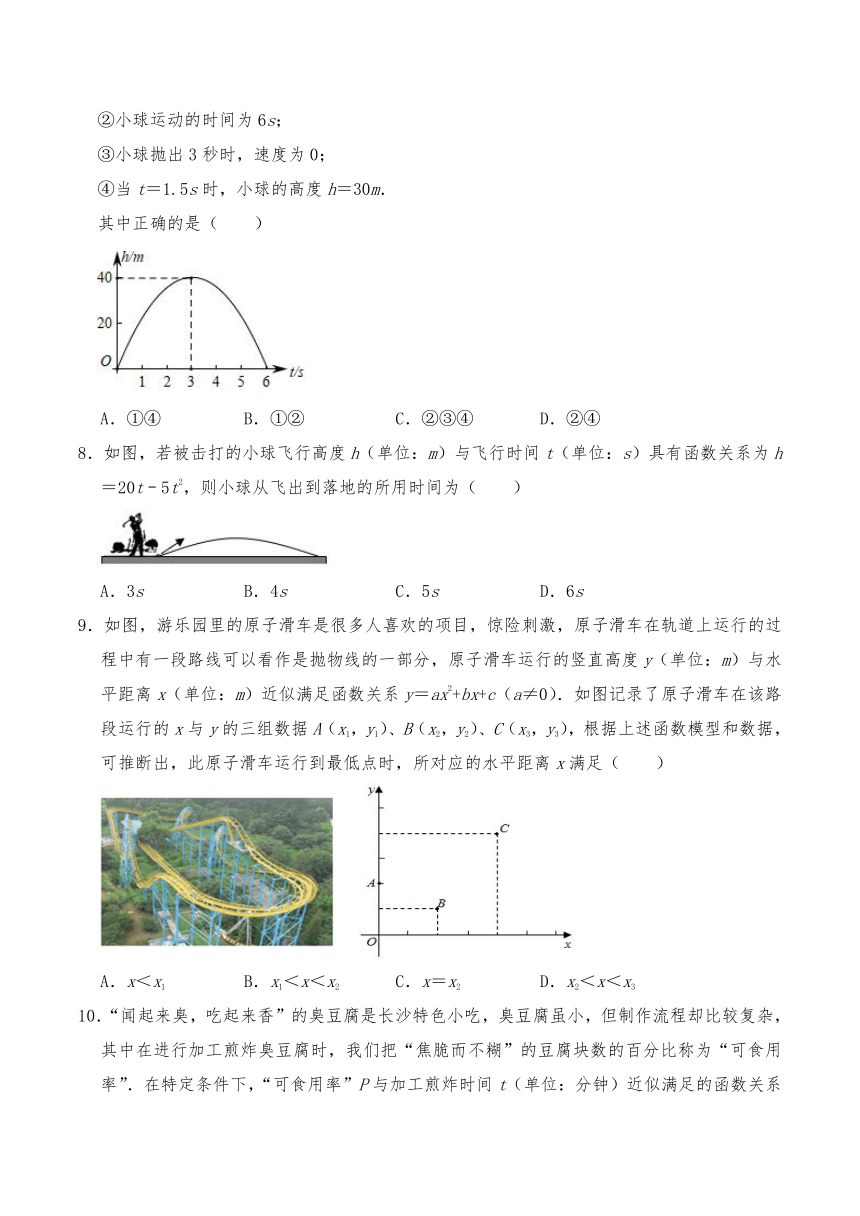
4.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球抛出3秒时达到最高点;②小球从抛出到落地经过的路程是80m;③小球的高度h=20时,t=1s或5s.④小球抛出2秒后的高度是35m.其中正确的有( )
A.①② B.②③ C.①③④ D.①②③
5.对于向上抛出的物体,在没有空气阻力的条件下,满足这样的关系式:h=vtgt2,其中h是上升高度,v是初始速度,g为重力加速度(g≈10m/s2),t为抛出后的时间.若v=20m/s,则下列说法正确的是( )
A.当h=20m时,对应两个不同的时刻点
B.当h=25 m时,对应一个时刻点
C.当h=15m时,对应两个不同的时刻点
D.h取任意值,均对应两个不同的时刻点
6.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),下列结论错误的是( )
A.图象具有对称性,对称轴是直线x=1
B.当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大
C.当x=﹣1或x=3时,函数最小值是0
D.当x=1时,函数的最大值是4
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
8.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为h=20t﹣5t2,则小球从飞出到落地的所用时间为( )
A.3s B.4s C.5s D.6s
9.如图,游乐园里的原子滑车是很多人喜欢的项目,惊险刺激,原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,原子滑车运行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了原子滑车在该路段运行的x与y的三组数据A(x1,y1)、B(x2,y2)、C(x3,y3),根据上述函数模型和数据,可推断出,此原子滑车运行到最低点时,所对应的水平距离x满足( )
A.x<x1 B.x1<x<x2 C.x=x2 D.x2<x<x3
10.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
二、填空题
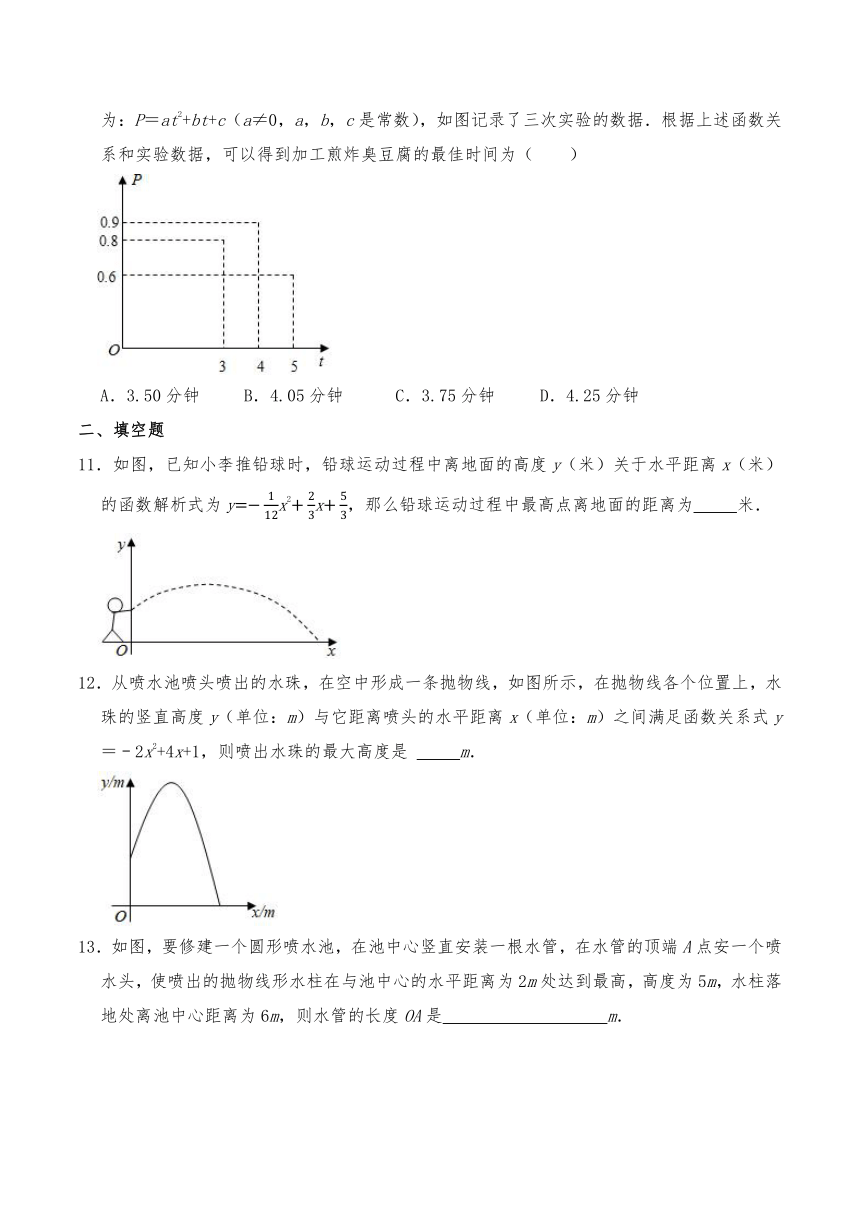
11.如图,已知小李推铅球时,铅球运动过程中离地面的高度y(米)关于水平距离x(米)的函数解析式为yx2x,那么铅球运动过程中最高点离地面的距离为 米.
12.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是 m.
13.如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端A点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为2m处达到最高,高度为5m,水柱落地处离池中心距离为6m,则水管的长度OA是 m.
14.一个球从地面上竖直向上弹起的过程中,距离地面高度h(米)与经过的时间t(秒)满足以下函数关系:h=﹣5t2+15t,则该球从弹起回到地面需要经过 秒,距离地面的最大高度为 米.
15.如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为 .
16.如图,杂技团进行杂技表演,一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为 米.
17.如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式h(t﹣6)2+5,则沙包在飞行过程中距离地面的最大高度是 米,此时飞行时间为 秒.
18.已知二次函数y与自变量x的部分对应值如表:
x … ﹣3 ﹣2 0 1 3 4 8 …
y … 7 0 ﹣8 ﹣9 ﹣5 0 40 …
则二次函数的解析式为 .
三、解答题
19.一个物体从地面竖直向上抛,有这样的关系式:h=vtgt2(不计空气阻力),其中h是物体距离地面的高度,v是初速度,g是重力加速度(g取10m/s2),t是抛出后所经历的时间.圆圆用发射器(发射器的高度忽略不计)将一个小球以10m/s的初速度从地面竖直向上抛.
(1)当小球的高度为1.8米时,求时间t的值;
(2)小球的高度能达到5.4米吗?请作出判断,并说明理由;
(3)若方方在圆圆抛出之后将另一个完全相同的小球以相同的速度从地面竖直向上抛,这两个小球在某一时刻的高度均为4.2米,求方方与圆圆抛球的时间差.
20.如图,在一次足球比赛中,守门员在地面O处将球踢出,一运动员在离守门员8米的A处发现球在自己头上的正上方4米处达到最高点M,球落地后又一次弹起.据实验测算,足球在空中运行的路线是一条抛物线,在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球第一次落地之前的运动路线的函数表达式及第一次落地点B和守门员(点O)的距离;
(2)运动员(点A)要抢到第二个落点C,他应再向前跑多少米?(假设点O、A、B、C在同一条直线上,结果保留根号)
21.某小区发现一名新型冠状病毒无症状感染者,政府决定对该小区所有居民进行核酸检测.从上午8:00起第x分钟等候检测的居民人数为y人,且y与x成二次函数关系(如图所示),已知在第10分钟时,等候检测的人数达到最大值150人.
(1)求0~10分钟内,y与x的函数解析式.
(2)若8:00起检测人员开始工作,共设两个检测岗,已知每岗每分钟可让检测完毕的5个居民离开,问检测开始后,第几分钟等候检测的居民人数最多,是多少人?
22.在篮球比赛中,小昆投出的球在点A(0,2)处反弹,反弹后球运动的路线为抛物线y1的一部分,抛物线顶点为点B(1,3).
(1)求该抛物线y1的函数表达式;当球运动到点C时被小昆抢到,CD⊥x轴于点D.CD=2.求点C的坐标;
(2)小昆抢到球后,立即在点C把球传出,此时球经过的路线为抛物线y2=mx2x(m为待定系数),试问篮球是否经过点E(9,3)?请说明理由.
23.已知,足球球门高2.44米,宽7.32米(如图1)在射门训练中,一球员接传球后射门,击球点A距离地面0.4米,即AB=0.4米,球的运动路线是抛物线的一部分,当球的水平移动距离BC为6米时,球恰好到达最高点D,即CD=4.4米.以直线BC为x轴,以直线AB为y轴建立平面直角坐标系(如图2).
(1)求该抛物线的表达式;
(2)若足球恰好击中球门横梁,求该足球运动的水平距离;
(3)若要使球直接落在球门内,则该球员应后退m米后接球射门,击球点为A'(如图3),请直接写出m的取值范围.
24.我州拥有充足的日照、优质的水源和土壤,非常利于冬草莓种植,但草莓的产量对培育技术要求很高.某基地为降低成本、提高产量,发现基地草莓的生长率p与温度t(℃)有如下关系:如图,当10≤t≤25时可近似用函数pt刻画;当25≤t≤37时可近似用函数p(t﹣h)2+0.4刻画.按照经验,基地草莓提前上市的天数m(天)与生长率p之间满足已学过的函数关系,部分数据如下:
生长率p 0.2 0.25 0.3 0.35
提前上市的天数m(天) 0 5 10 15
(1)求h的值;
(2)写出m关于p的函数表达式;
(3)用含t的代数式表示m;
(4)天气寒冷,大棚加温可改变草莓生长速度.大棚恒温20℃时每天的成本为100元,计划该作物30天后上市,现根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25时的成本为200元/天.但若欲加温到25<t≤37,由于要采用特殊方法,成本增加到400元/天.问加温到多少度时增加的利润最大?并说明理由.(注:假如草莓上市售出后大棚暂停使用)
答案
一、选择题
B.A.C.A.C.D.C.B.B.C.
二、填空题
11.3.12.3. 13.. 14.3,. 15.yx2x.
16.3.4. 17.5;6. 18.y=x2﹣2x﹣8
三、解答题
19.(1)把v=10,g=10代入h=vtgt2得:
h=﹣5t2+10t,
当h=1.8时,
1.8=﹣5t2+10t,
即5t2﹣10t+1.8=0,
解得:t1=0.2,t2=1.8
答:小球的高度为1.8米时,所用时间为0.2s或1.8s;
(2)小球的高度不能达到5.4米,
理由如下:
把t=5.4代入h=﹣5t2+10t得:
5.4=﹣5t2+10t,
∴5t2﹣10t+5.4=0,
∵△=(﹣10)2﹣4×5×5.4=﹣8<0,
∴5.4=﹣5t2+10t无实数解,
∴小球的高度不能达到5.4米;
(3)由题意得:4.2=﹣5t2+10t,
∴5t2﹣10t+4.2=0,
解得:t1==0.6,t2=1.4,
t2﹣t1=0.8,
答:方方与圆圆抛球的时间差为0.8s.
20.(1)设足球第一次落地之前的运动路线的函数表达式为y=a(x﹣8)2+4,根据其顶点为(8,4),过点O(0,0)得
0=64a+4,
解得:a,
∴y(x﹣8)2+4.
当y=0时,(﹣8)2+4=0,
解得:x=0(舍去)或x=16,
答:足球第一次落地之前的运动路线的函数表达式为y(x﹣8)2+4,第一次落地点B和守门员(点O)的距离为16米;
(2)设第一次落地之后的运动路线的函数表达式为y(x﹣m)2+2,由题意,得
0(16﹣m)2+2,
解得m=16+4或m=16﹣4(舍去),
∴y(x﹣16﹣4)2+2.
当y=0时,
0(x﹣16﹣4)2+2.
解得:x=16+8或x=16.
∴他应从第一次落地点C再向前跑的距离为:
16+88=(8+8)米.
答:他应再向前跑(8+8)米.
21.(1)由题意可知,抛物线的顶点坐标为(10,150),
∴设0~10分钟内,y与x的函数解析式为y=a(x﹣10)2+150,
将(0,50)代入,得:
50=a(0﹣10)2+150,
解得a=﹣1,
∴y=﹣(x﹣10)2+150
=﹣x2+20x+50,
∴0~10分钟内,y与x的函数解析式为y=﹣x2+20x+50.
(2)∵两个检测岗,每岗每分钟可让检测完毕的5个居民离开,
∴每分钟共可检测10人,
∴第x分钟等候检测的居民人数为:
y=﹣x2+20x+50﹣10x
=﹣x2+10x+50
=﹣(x﹣5)2+75,
∴当x=5时,y有最大值,最大值为75.
∴检测开始后,第5分钟等候检测的居民人数最多,为75人.
22.(1)设函数表达式为,
把点A(0,2)代入得:a(0﹣1)2+3=2,
解得a=﹣1,
∴,
令y1=2得﹣x2+2x+2=2,
解得x1=0,x2=2,
∴C(2,2);
(2)把点C(2,2)代入得;
解得:,
故,
当x=9时,y23,
所以,不经过E(9,3).
23.(1)抛物线的顶点坐标是(6,4.4),
设抛物线的解析式是:y=a(x﹣6)2+4.4,
把(0,0.4)代入得36a+4.4=0.4,
解得a,
则抛物线是y(x﹣6)2+4.4;
(2)∵球门高为2.44米,即y=2.44,
则有2.44(x﹣6)2+4.4,
解得:x1=10.2,x2=1.8,
从题干图2中,发现球门在CD右边,
∴x=10.2,
即足球运动的水平距离是10.2米;
(3)不后退时,刚好击中横梁,
∴往后退,则球可以进入球门,
而当球落地时,球刚好在门口,是一个临界值,
当y=0时,
有0(x﹣6)2+4.4,
解得:x1=6,x2=6,
取正值,x=6,
∴后退的距离需小于610.2=(4.2)米
故0<m4.2.
24.(1)把(25,0.3)代入p(t﹣h)2+0.4,得:
0.3(25﹣h)2+0.4,
解得:h=29或h=21,
∵25≤t≤37,
∴h=29.
(2)由表格可知,m是p的一次函数,
设m=kp+b,
把(0.2,0),(0.3,10)代入得:,
解得:,
∴m=100p﹣20.
(3)当t=29时,提前20天上市,增加的利润最大,理由如下:
当10≤t≤25时,pt,
∴m=100(t)﹣20=2t﹣40;
当25≤t≤37时,p(t﹣h)2+0.4,
∴m=100[(t﹣h)2+0.4]﹣20(t﹣29)2+20,
∴m;
(4)当20≤t≤25时,增加的利润为:
600m+[100×30﹣200(30﹣m)]=800m﹣3000=1600t﹣35000,
当t=25时,增加的利润的最大值为1600×25﹣35000=5000元;
当25<t≤37时,增加的利润为:
600m+[100×30﹣400(30﹣m)]=1000m﹣9000=﹣625(t﹣29)2+11000,
∴当t=29时,增加的利润的最大值为11000元.
综上,当t=29时,提前20天上市,增加的利润最大,最大值为11000元.
一、选择题
1.在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为yx2x,由此可知小宇此次实心球训练的成绩为( )
A.米 B.8米 C.10米 D.2米
2.以固定的初速度v0(米/秒)向上抛一个小球,小球的高度h(米)与小球的运动时间t(秒)之间的关系式是h=v0t﹣4.9t2,在这个关系式中,常量为( )
A.﹣4.9和v0 B.v0和t C.t D.h
3.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+3,则下列结论错误的是( )
A.柱子OA的高度为3m
B.喷出的水流距柱子1m处达到最大高度
C.喷出的水流距水平面的最大高度是3m
D.水池的半径至少要3m才能使喷出的水流不至于落在池外
4.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:①小球抛出3秒时达到最高点;②小球从抛出到落地经过的路程是80m;③小球的高度h=20时,t=1s或5s.④小球抛出2秒后的高度是35m.其中正确的有( )
A.①② B.②③ C.①③④ D.①②③
5.对于向上抛出的物体,在没有空气阻力的条件下,满足这样的关系式:h=vtgt2,其中h是上升高度,v是初始速度,g为重力加速度(g≈10m/s2),t为抛出后的时间.若v=20m/s,则下列说法正确的是( )
A.当h=20m时,对应两个不同的时刻点
B.当h=25 m时,对应一个时刻点
C.当h=15m时,对应两个不同的时刻点
D.h取任意值,均对应两个不同的时刻点
6.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),下列结论错误的是( )
A.图象具有对称性,对称轴是直线x=1
B.当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大
C.当x=﹣1或x=3时,函数最小值是0
D.当x=1时,函数的最大值是4
7.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
8.如图,若被击打的小球飞行高度h(单位:m)与飞行时间t(单位:s)具有函数关系为h=20t﹣5t2,则小球从飞出到落地的所用时间为( )
A.3s B.4s C.5s D.6s
9.如图,游乐园里的原子滑车是很多人喜欢的项目,惊险刺激,原子滑车在轨道上运行的过程中有一段路线可以看作是抛物线的一部分,原子滑车运行的竖直高度y(单位:m)与水平距离x(单位:m)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了原子滑车在该路段运行的x与y的三组数据A(x1,y1)、B(x2,y2)、C(x3,y3),根据上述函数模型和数据,可推断出,此原子滑车运行到最低点时,所对应的水平距离x满足( )
A.x<x1 B.x1<x<x2 C.x=x2 D.x2<x<x3
10.“闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”.在特定条件下,“可食用率”P与加工煎炸时间t(单位:分钟)近似满足的函数关系为:P=at2+bt+c(a≠0,a,b,c是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( )
A.3.50分钟 B.4.05分钟 C.3.75分钟 D.4.25分钟
二、填空题
11.如图,已知小李推铅球时,铅球运动过程中离地面的高度y(米)关于水平距离x(米)的函数解析式为yx2x,那么铅球运动过程中最高点离地面的距离为 米.
12.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是 m.
13.如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端A点安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为2m处达到最高,高度为5m,水柱落地处离池中心距离为6m,则水管的长度OA是 m.
14.一个球从地面上竖直向上弹起的过程中,距离地面高度h(米)与经过的时间t(秒)满足以下函数关系:h=﹣5t2+15t,则该球从弹起回到地面需要经过 秒,距离地面的最大高度为 米.
15.如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为 .
16.如图,杂技团进行杂技表演,一名演员从跷跷板右端A处恰好弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线的一部分,跳起的演员距点A所在y轴的水平距离为2.5米时身体离地面最高.若人梯到起跳点A的水平距离为4米,则人梯BC的高为 米.
17.如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式h(t﹣6)2+5,则沙包在飞行过程中距离地面的最大高度是 米,此时飞行时间为 秒.
18.已知二次函数y与自变量x的部分对应值如表:
x … ﹣3 ﹣2 0 1 3 4 8 …
y … 7 0 ﹣8 ﹣9 ﹣5 0 40 …
则二次函数的解析式为 .
三、解答题
19.一个物体从地面竖直向上抛,有这样的关系式:h=vtgt2(不计空气阻力),其中h是物体距离地面的高度,v是初速度,g是重力加速度(g取10m/s2),t是抛出后所经历的时间.圆圆用发射器(发射器的高度忽略不计)将一个小球以10m/s的初速度从地面竖直向上抛.
(1)当小球的高度为1.8米时,求时间t的值;
(2)小球的高度能达到5.4米吗?请作出判断,并说明理由;
(3)若方方在圆圆抛出之后将另一个完全相同的小球以相同的速度从地面竖直向上抛,这两个小球在某一时刻的高度均为4.2米,求方方与圆圆抛球的时间差.
20.如图,在一次足球比赛中,守门员在地面O处将球踢出,一运动员在离守门员8米的A处发现球在自己头上的正上方4米处达到最高点M,球落地后又一次弹起.据实验测算,足球在空中运行的路线是一条抛物线,在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球第一次落地之前的运动路线的函数表达式及第一次落地点B和守门员(点O)的距离;
(2)运动员(点A)要抢到第二个落点C,他应再向前跑多少米?(假设点O、A、B、C在同一条直线上,结果保留根号)
21.某小区发现一名新型冠状病毒无症状感染者,政府决定对该小区所有居民进行核酸检测.从上午8:00起第x分钟等候检测的居民人数为y人,且y与x成二次函数关系(如图所示),已知在第10分钟时,等候检测的人数达到最大值150人.
(1)求0~10分钟内,y与x的函数解析式.
(2)若8:00起检测人员开始工作,共设两个检测岗,已知每岗每分钟可让检测完毕的5个居民离开,问检测开始后,第几分钟等候检测的居民人数最多,是多少人?
22.在篮球比赛中,小昆投出的球在点A(0,2)处反弹,反弹后球运动的路线为抛物线y1的一部分,抛物线顶点为点B(1,3).
(1)求该抛物线y1的函数表达式;当球运动到点C时被小昆抢到,CD⊥x轴于点D.CD=2.求点C的坐标;
(2)小昆抢到球后,立即在点C把球传出,此时球经过的路线为抛物线y2=mx2x(m为待定系数),试问篮球是否经过点E(9,3)?请说明理由.
23.已知,足球球门高2.44米,宽7.32米(如图1)在射门训练中,一球员接传球后射门,击球点A距离地面0.4米,即AB=0.4米,球的运动路线是抛物线的一部分,当球的水平移动距离BC为6米时,球恰好到达最高点D,即CD=4.4米.以直线BC为x轴,以直线AB为y轴建立平面直角坐标系(如图2).
(1)求该抛物线的表达式;
(2)若足球恰好击中球门横梁,求该足球运动的水平距离;
(3)若要使球直接落在球门内,则该球员应后退m米后接球射门,击球点为A'(如图3),请直接写出m的取值范围.
24.我州拥有充足的日照、优质的水源和土壤,非常利于冬草莓种植,但草莓的产量对培育技术要求很高.某基地为降低成本、提高产量,发现基地草莓的生长率p与温度t(℃)有如下关系:如图,当10≤t≤25时可近似用函数pt刻画;当25≤t≤37时可近似用函数p(t﹣h)2+0.4刻画.按照经验,基地草莓提前上市的天数m(天)与生长率p之间满足已学过的函数关系,部分数据如下:
生长率p 0.2 0.25 0.3 0.35
提前上市的天数m(天) 0 5 10 15
(1)求h的值;
(2)写出m关于p的函数表达式;
(3)用含t的代数式表示m;
(4)天气寒冷,大棚加温可改变草莓生长速度.大棚恒温20℃时每天的成本为100元,计划该作物30天后上市,现根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25时的成本为200元/天.但若欲加温到25<t≤37,由于要采用特殊方法,成本增加到400元/天.问加温到多少度时增加的利润最大?并说明理由.(注:假如草莓上市售出后大棚暂停使用)
答案
一、选择题
B.A.C.A.C.D.C.B.B.C.
二、填空题
11.3.12.3. 13.. 14.3,. 15.yx2x.
16.3.4. 17.5;6. 18.y=x2﹣2x﹣8
三、解答题
19.(1)把v=10,g=10代入h=vtgt2得:
h=﹣5t2+10t,
当h=1.8时,
1.8=﹣5t2+10t,
即5t2﹣10t+1.8=0,
解得:t1=0.2,t2=1.8
答:小球的高度为1.8米时,所用时间为0.2s或1.8s;
(2)小球的高度不能达到5.4米,
理由如下:
把t=5.4代入h=﹣5t2+10t得:
5.4=﹣5t2+10t,
∴5t2﹣10t+5.4=0,
∵△=(﹣10)2﹣4×5×5.4=﹣8<0,
∴5.4=﹣5t2+10t无实数解,
∴小球的高度不能达到5.4米;
(3)由题意得:4.2=﹣5t2+10t,
∴5t2﹣10t+4.2=0,
解得:t1==0.6,t2=1.4,
t2﹣t1=0.8,
答:方方与圆圆抛球的时间差为0.8s.
20.(1)设足球第一次落地之前的运动路线的函数表达式为y=a(x﹣8)2+4,根据其顶点为(8,4),过点O(0,0)得
0=64a+4,
解得:a,
∴y(x﹣8)2+4.
当y=0时,(﹣8)2+4=0,
解得:x=0(舍去)或x=16,
答:足球第一次落地之前的运动路线的函数表达式为y(x﹣8)2+4,第一次落地点B和守门员(点O)的距离为16米;
(2)设第一次落地之后的运动路线的函数表达式为y(x﹣m)2+2,由题意,得
0(16﹣m)2+2,
解得m=16+4或m=16﹣4(舍去),
∴y(x﹣16﹣4)2+2.
当y=0时,
0(x﹣16﹣4)2+2.
解得:x=16+8或x=16.
∴他应从第一次落地点C再向前跑的距离为:
16+88=(8+8)米.
答:他应再向前跑(8+8)米.
21.(1)由题意可知,抛物线的顶点坐标为(10,150),
∴设0~10分钟内,y与x的函数解析式为y=a(x﹣10)2+150,
将(0,50)代入,得:
50=a(0﹣10)2+150,
解得a=﹣1,
∴y=﹣(x﹣10)2+150
=﹣x2+20x+50,
∴0~10分钟内,y与x的函数解析式为y=﹣x2+20x+50.
(2)∵两个检测岗,每岗每分钟可让检测完毕的5个居民离开,
∴每分钟共可检测10人,
∴第x分钟等候检测的居民人数为:
y=﹣x2+20x+50﹣10x
=﹣x2+10x+50
=﹣(x﹣5)2+75,
∴当x=5时,y有最大值,最大值为75.
∴检测开始后,第5分钟等候检测的居民人数最多,为75人.
22.(1)设函数表达式为,
把点A(0,2)代入得:a(0﹣1)2+3=2,
解得a=﹣1,
∴,
令y1=2得﹣x2+2x+2=2,
解得x1=0,x2=2,
∴C(2,2);
(2)把点C(2,2)代入得;
解得:,
故,
当x=9时,y23,
所以,不经过E(9,3).
23.(1)抛物线的顶点坐标是(6,4.4),
设抛物线的解析式是:y=a(x﹣6)2+4.4,
把(0,0.4)代入得36a+4.4=0.4,
解得a,
则抛物线是y(x﹣6)2+4.4;
(2)∵球门高为2.44米,即y=2.44,
则有2.44(x﹣6)2+4.4,
解得:x1=10.2,x2=1.8,
从题干图2中,发现球门在CD右边,
∴x=10.2,
即足球运动的水平距离是10.2米;
(3)不后退时,刚好击中横梁,
∴往后退,则球可以进入球门,
而当球落地时,球刚好在门口,是一个临界值,
当y=0时,
有0(x﹣6)2+4.4,
解得:x1=6,x2=6,
取正值,x=6,
∴后退的距离需小于610.2=(4.2)米
故0<m4.2.
24.(1)把(25,0.3)代入p(t﹣h)2+0.4,得:
0.3(25﹣h)2+0.4,
解得:h=29或h=21,
∵25≤t≤37,
∴h=29.
(2)由表格可知,m是p的一次函数,
设m=kp+b,
把(0.2,0),(0.3,10)代入得:,
解得:,
∴m=100p﹣20.
(3)当t=29时,提前20天上市,增加的利润最大,理由如下:
当10≤t≤25时,pt,
∴m=100(t)﹣20=2t﹣40;
当25≤t≤37时,p(t﹣h)2+0.4,
∴m=100[(t﹣h)2+0.4]﹣20(t﹣29)2+20,
∴m;
(4)当20≤t≤25时,增加的利润为:
600m+[100×30﹣200(30﹣m)]=800m﹣3000=1600t﹣35000,
当t=25时,增加的利润的最大值为1600×25﹣35000=5000元;
当25<t≤37时,增加的利润为:
600m+[100×30﹣400(30﹣m)]=1000m﹣9000=﹣625(t﹣29)2+11000,
∴当t=29时,增加的利润的最大值为11000元.
综上,当t=29时,提前20天上市,增加的利润最大,最大值为11000元.
