九年级数学上册试题 21.5.2反比例函数的应用-沪科版(含答案)
文档属性
| 名称 | 九年级数学上册试题 21.5.2反比例函数的应用-沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 109.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 22:30:13 | ||
图片预览


文档简介
21.5.2反比例函数的应用
一、选择题
1.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P(S≠0),这个函数的图象大致是( )
A. B.
C. D.
2.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
3.某物体对地面的压力为定值,物体对地面的压强P(Pa)与受力面积S(m2)之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
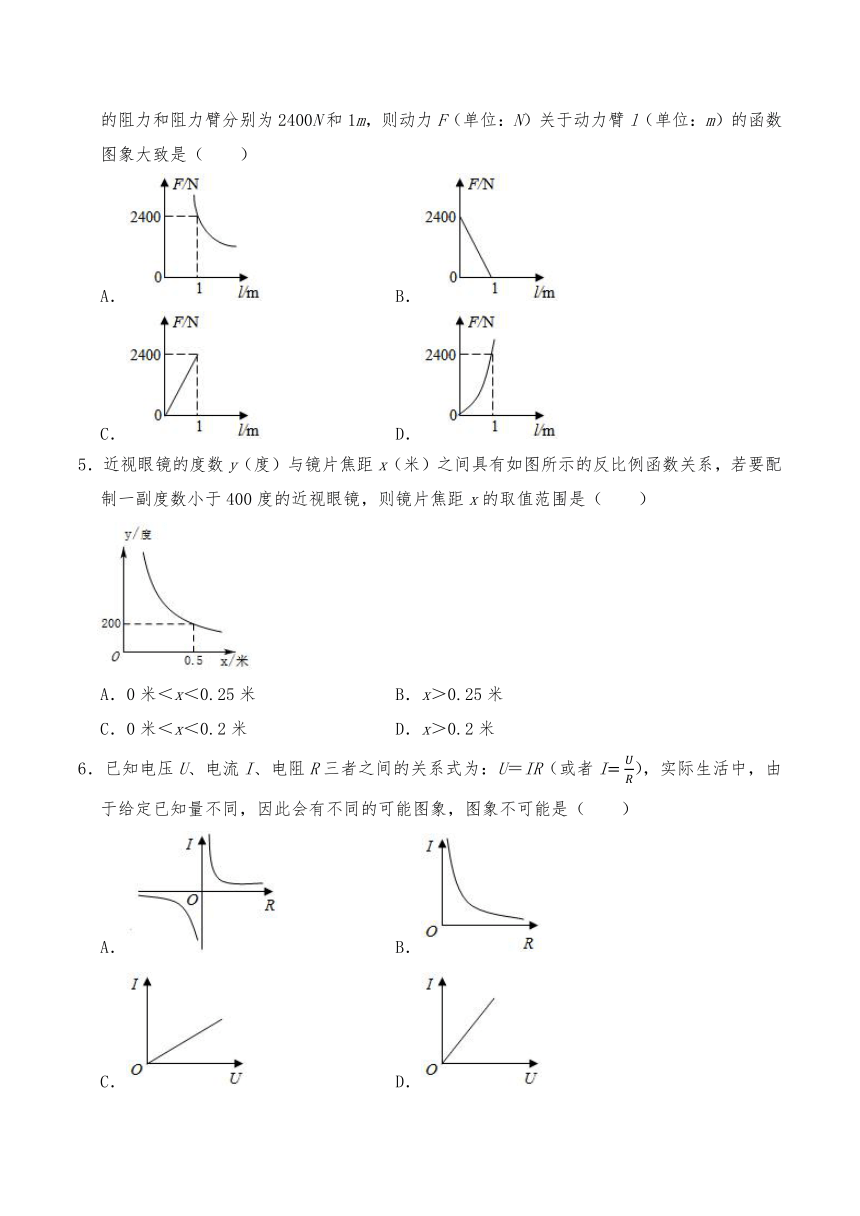
4.小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是( )
A. B.
C. D.
5.近视眼镜的度数y(度)与镜片焦距x(米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近视眼镜,则镜片焦距x的取值范围是( )
A.0米<x<0.25米 B.x>0.25米
C.0米<x<0.2米 D.x>0.2米
6.已知电压U、电流I、电阻R三者之间的关系式为:U=IR(或者I),实际生活中,由于给定已知量不同,因此会有不同的可能图象,图象不可能是( )
A. B.
C. D.
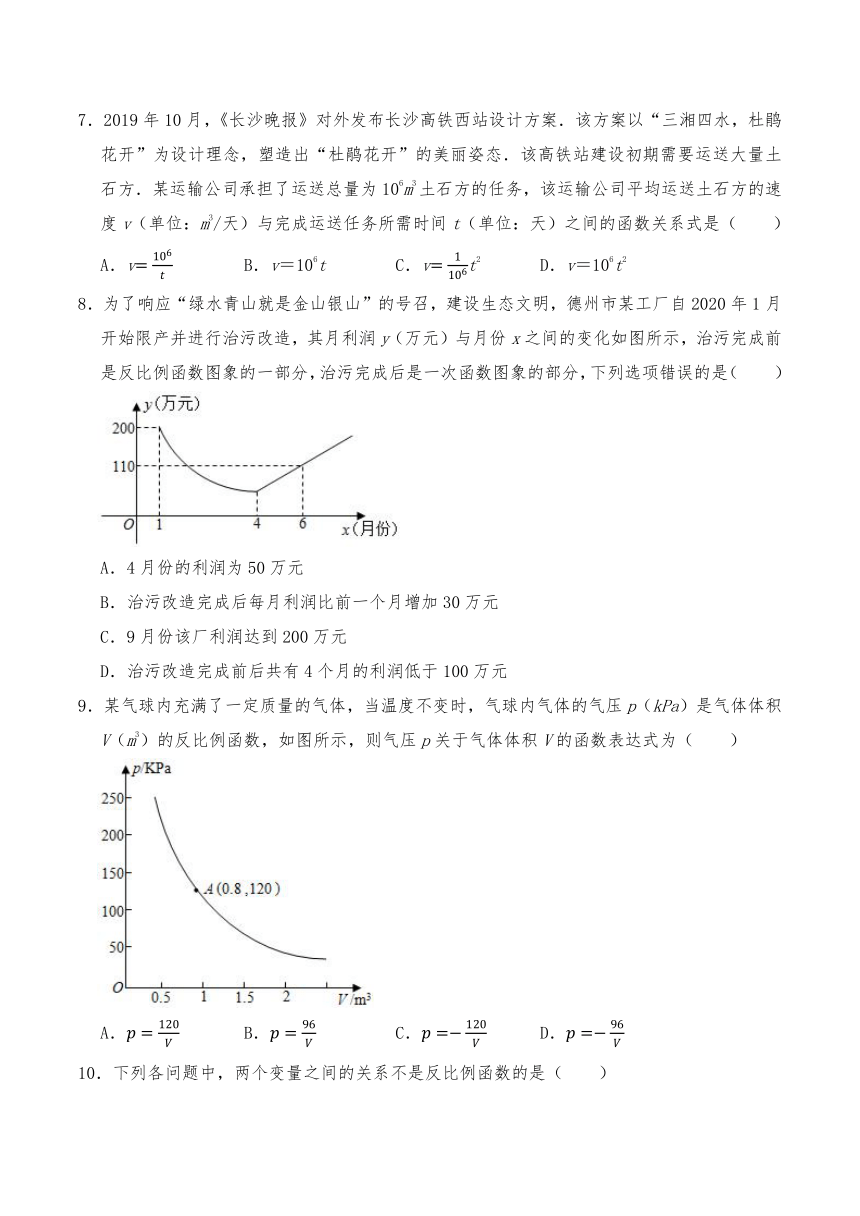
7.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A.v B.v=106t C.vt2 D.v=106t2
8.为了响应“绿水青山就是金山银山”的号召,建设生态文明,德州市某工厂自2020年1月开始限产并进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.9月份该厂利润达到200万元
D.治污改造完成前后共有4个月的利润低于100万元
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,如图所示,则气压p关于气体体积V的函数表达式为( )
A. B. C. D.
10.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100m 赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系
B.菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系
C.一个玻璃容器的体积为30L时,所盛液体的质量m 与所盛液体的密度ρ之间的关系
D.压力为600N时,压强p与受力面积S之间的关系
二、填空题
11.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t= (v>0).
12.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.则其函数解析式为 .
13.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
14.面积一定的长方形,长为8时,宽为5,当长为10时,宽为 .
15.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(4,3)在图象上,则当力达到10N时,物体在力的方向上移动的距离是 m.
16.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
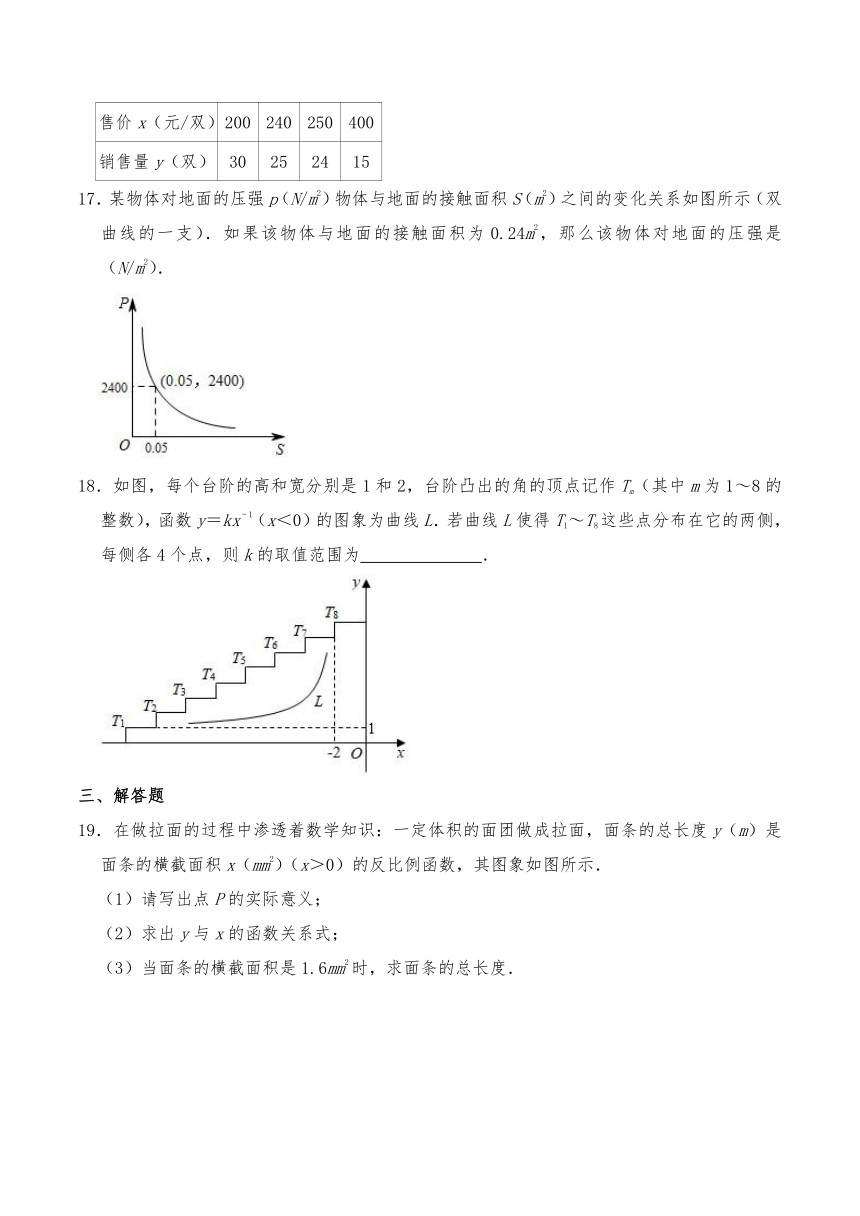
17.某物体对地面的压强p(N/m2)物体与地面的接触面积S(m2)之间的变化关系如图所示(双曲线的一支).如果该物体与地面的接触面积为0.24m2,那么该物体对地面的压强是 (N/m2).
18.如图,每个台阶的高和宽分别是1和2,台阶凸出的角的顶点记作Tm(其中m为1~8的整数),函数y=kx﹣1(x<0)的图象为曲线L.若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的取值范围为 .
三、解答题
19.在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的横截面积x(mm2)(x>0)的反比例函数,其图象如图所示.
(1)请写出点P的实际意义;
(2)求出y与x的函数关系式;
(3)当面条的横截面积是1.6mm2时,求面条的总长度.
20.南宁至玉林高速铁路已于去年开工建设.玉林良睦隧道是全线控制性工程,首期打通共有土石方总量为600千立方米,设计划平均每天挖掘土石方x千立方米,总需用时间y天,且完成首期工程限定时间不超过600天.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天挖掘土石方比原计划多0.2千立方米,工期比原计划提前了100天完成,求实际挖掘了多少天才能完成首期工程?
21.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)恒温系统设定的恒定温度为 ;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,为避免蔬菜受到伤害,恒温系统最多可以关闭多少小时?
22.教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降.水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40℃的开水,则他需要在什么时间段内接水?
23.如图,小明想要用撬棍撬动一块大石头,已知阻力为1200N,阻力臂长为0.5m.设动力为y(N),动力臂长为x(m).(杠杆平衡时,动力×动力臂=阻力×阻力臂,图中撬棍本身所受的重力略去不计.)
(1)求y关于x的函数表达式.
(2)当动力臂长为1.5m时,撬动石头至少需要多大的力?
(3)小明若想使动力不超过300N,在动力臂最大为1.8m的条件下,他能否撬动这块石头?请说明理由.
24.某汽车销售商推出分期付款购车促销活动,交付首付款后,余额要在30个月内结清,不计算利息,王先生在活动期间购买了价格为12万元的汽车,交了首付款后平均每月付款y万元,x个月结清.y与x的函数关系如图所示,根据图象回答下列问题:
(1)确定y与x的函数解析式,并求出首付款的数目;
(2)王先生若用20个月结清,平均每月应付多少万元?
(3)如果打算每月付款不超过4000元,王先生至少要几个月才能结清余额?
答案
一、选择题
A.B.B.A.B.A.A.D.B.C.
二、填空题
11.. 12.P. 13.y(x>0). 14.4.
15.1.2. 16.300. 17.500. 18.﹣36<k<﹣28.
三、解答题
19.(1)由图象知,点P的实际意义是:当面条的横截面积是4mm2时,面条的总长度是32m;
(2)设y与x的函数关系式为y,
∵反比例函数图象经过点(4,32),
∴32,解得k=128,
∴y与x的函数关系式是y(x>0);
(3)当x=1.6时,y80.
答:面条的总长度是80m.
20.(1)根据题意可得:y,
∵y≤600,
∴x≥1;
(2)设实际挖掘了m天才能完成首期工程,根据题意可得:
0.2,
解得:m=﹣600(舍)或500,
检验得:m=500是原方程的根,
答:实际挖掘了500天才能完成首期工程.
21.(1)设线段AB解析式为y=k1x+b(k≠0),
∵线段AB过点(0,10),(2,14),
代入得,
解得,
∴AB解析式为:y=2x+10(0≤x<5),
∵B在线段AB上当x=5时,y=20,
∴B坐标为(5,20),
∴线段BC的解析式为:y=20(5≤x<10),
设双曲线CD解析式为:y(k2≠0),
∵C(10,20),
∴k2=200,
∴双曲线CD解析式为:y(10≤x≤24);
∴y关于x的函数解析式为:
y;
(2)由(1)恒温系统设定恒温为20℃,
故答案为:20℃;
(3)把y=10代入y中,解得,x=20,
∴20﹣10=10,
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
22.(1)当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)的坐标分别代入y=k1x+b得,
解得k1=10,b=20.
∴当0≤x≤8时,y=10x+20.
当8<x≤a时,设y,
将(8,100)的坐标代入y,
得k2=800
∴当8<x≤a时,y.
综上,当0≤x≤8时,y=10x+20;当8<x≤a时,y;
(2)将y=20代入y,
解得x=40,
即a=40;
(3)当y=40时,x20.
∴要想喝到不低于40℃的开水,x需满足8≤x≤20,
即李老师要在7:38到7:50之间接水.
23.(1)由题意可得:xy=1200×0.5,
则y,
即y关于x的函数表达式为y;
(2)∵y,
∴当x=1.5时,y400,
故当动力臂长为1.5m时,撬动石头至少需要400N的力;
(3)他不能撬动这块石头,理由如下:
∵y,
∴x,
∵0<x≤1.8,
∴01.8,
∴y≥333,
∵333300,
∴他不能撬动这块石头.
24.(1)由图象可知y与x成反比例,设y与x的函数关系式为y,
把(5,1.8)代入关系式得1.8,
∴k=9,
∴y,
∴12﹣9=3(万元).
答:首付款为3万元;
(2)当x=20时,y0.45(万元),
答:每月应付0.45万元;
(3)当y=0.4时,0.4,
解得:x,
答:他至少23个月才能结清余款.
一、选择题
1.当压力F(N)一定时,物体所受的压强P(Pa)与受力面积S(m2)的函数关系式为P(S≠0),这个函数的图象大致是( )
A. B.
C. D.
2.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
3.某物体对地面的压力为定值,物体对地面的压强P(Pa)与受力面积S(m2)之间的函数关系如图所示,这一函数表达式为( )
A. B. C. D.
4.小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m,则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是( )
A. B.
C. D.
5.近视眼镜的度数y(度)与镜片焦距x(米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近视眼镜,则镜片焦距x的取值范围是( )
A.0米<x<0.25米 B.x>0.25米
C.0米<x<0.2米 D.x>0.2米
6.已知电压U、电流I、电阻R三者之间的关系式为:U=IR(或者I),实际生活中,由于给定已知量不同,因此会有不同的可能图象,图象不可能是( )
A. B.
C. D.
7.2019年10月,《长沙晚报》对外发布长沙高铁西站设计方案.该方案以“三湘四水,杜鹃花开”为设计理念,塑造出“杜鹃花开”的美丽姿态.该高铁站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均运送土石方的速度v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A.v B.v=106t C.vt2 D.v=106t2
8.为了响应“绿水青山就是金山银山”的号召,建设生态文明,德州市某工厂自2020年1月开始限产并进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.9月份该厂利润达到200万元
D.治污改造完成前后共有4个月的利润低于100万元
9.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,如图所示,则气压p关于气体体积V的函数表达式为( )
A. B. C. D.
10.下列各问题中,两个变量之间的关系不是反比例函数的是( )
A.小明完成100m 赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的关系
B.菱形的面积为48cm2,它的两条对角线的长为y(cm)与x(cm)的关系
C.一个玻璃容器的体积为30L时,所盛液体的质量m 与所盛液体的密度ρ之间的关系
D.压力为600N时,压强p与受力面积S之间的关系
二、填空题
11.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t= (v>0).
12.某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.则其函数解析式为 .
13.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
14.面积一定的长方形,长为8时,宽为5,当长为10时,宽为 .
15.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(4,3)在图象上,则当力达到10N时,物体在力的方向上移动的距离是 m.
16.根据某商场对一款运动鞋五天中的售价与销量关系的调查显示,售价是销量的反比例函数(统计数据见下表).已知该运动鞋的进价为180元/双,要使该款运动鞋每天的销售利润达到2400元,则其售价应定为 元.
售价x(元/双) 200 240 250 400
销售量y(双) 30 25 24 15
17.某物体对地面的压强p(N/m2)物体与地面的接触面积S(m2)之间的变化关系如图所示(双曲线的一支).如果该物体与地面的接触面积为0.24m2,那么该物体对地面的压强是 (N/m2).
18.如图,每个台阶的高和宽分别是1和2,台阶凸出的角的顶点记作Tm(其中m为1~8的整数),函数y=kx﹣1(x<0)的图象为曲线L.若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的取值范围为 .
三、解答题
19.在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的横截面积x(mm2)(x>0)的反比例函数,其图象如图所示.
(1)请写出点P的实际意义;
(2)求出y与x的函数关系式;
(3)当面条的横截面积是1.6mm2时,求面条的总长度.
20.南宁至玉林高速铁路已于去年开工建设.玉林良睦隧道是全线控制性工程,首期打通共有土石方总量为600千立方米,设计划平均每天挖掘土石方x千立方米,总需用时间y天,且完成首期工程限定时间不超过600天.
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天挖掘土石方比原计划多0.2千立方米,工期比原计划提前了100天完成,求实际挖掘了多少天才能完成首期工程?
21.某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y(℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)恒温系统设定的恒定温度为 ;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,为避免蔬菜受到伤害,恒温系统最多可以关闭多少小时?
22.教师办公室有一种可以自动加热的饮水机,该饮水机的工作程序是:放满水后接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降.水温y(℃)和通电时间x(min)成反比例函数关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温均为20℃,接通电源后,水温y(℃)和通电时间x(min)之间的关系如图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的函数关系式;
(2)求出图中a的值;
(3)李老师这天早上7:30将饮水机电源打开,若他想在8:10上课前喝到不低于40℃的开水,则他需要在什么时间段内接水?
23.如图,小明想要用撬棍撬动一块大石头,已知阻力为1200N,阻力臂长为0.5m.设动力为y(N),动力臂长为x(m).(杠杆平衡时,动力×动力臂=阻力×阻力臂,图中撬棍本身所受的重力略去不计.)
(1)求y关于x的函数表达式.
(2)当动力臂长为1.5m时,撬动石头至少需要多大的力?
(3)小明若想使动力不超过300N,在动力臂最大为1.8m的条件下,他能否撬动这块石头?请说明理由.
24.某汽车销售商推出分期付款购车促销活动,交付首付款后,余额要在30个月内结清,不计算利息,王先生在活动期间购买了价格为12万元的汽车,交了首付款后平均每月付款y万元,x个月结清.y与x的函数关系如图所示,根据图象回答下列问题:
(1)确定y与x的函数解析式,并求出首付款的数目;
(2)王先生若用20个月结清,平均每月应付多少万元?
(3)如果打算每月付款不超过4000元,王先生至少要几个月才能结清余额?
答案
一、选择题
A.B.B.A.B.A.A.D.B.C.
二、填空题
11.. 12.P. 13.y(x>0). 14.4.
15.1.2. 16.300. 17.500. 18.﹣36<k<﹣28.
三、解答题
19.(1)由图象知,点P的实际意义是:当面条的横截面积是4mm2时,面条的总长度是32m;
(2)设y与x的函数关系式为y,
∵反比例函数图象经过点(4,32),
∴32,解得k=128,
∴y与x的函数关系式是y(x>0);
(3)当x=1.6时,y80.
答:面条的总长度是80m.
20.(1)根据题意可得:y,
∵y≤600,
∴x≥1;
(2)设实际挖掘了m天才能完成首期工程,根据题意可得:
0.2,
解得:m=﹣600(舍)或500,
检验得:m=500是原方程的根,
答:实际挖掘了500天才能完成首期工程.
21.(1)设线段AB解析式为y=k1x+b(k≠0),
∵线段AB过点(0,10),(2,14),
代入得,
解得,
∴AB解析式为:y=2x+10(0≤x<5),
∵B在线段AB上当x=5时,y=20,
∴B坐标为(5,20),
∴线段BC的解析式为:y=20(5≤x<10),
设双曲线CD解析式为:y(k2≠0),
∵C(10,20),
∴k2=200,
∴双曲线CD解析式为:y(10≤x≤24);
∴y关于x的函数解析式为:
y;
(2)由(1)恒温系统设定恒温为20℃,
故答案为:20℃;
(3)把y=10代入y中,解得,x=20,
∴20﹣10=10,
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
22.(1)当0≤x≤8时,设y=k1x+b,
将(0,20),(8,100)的坐标分别代入y=k1x+b得,
解得k1=10,b=20.
∴当0≤x≤8时,y=10x+20.
当8<x≤a时,设y,
将(8,100)的坐标代入y,
得k2=800
∴当8<x≤a时,y.
综上,当0≤x≤8时,y=10x+20;当8<x≤a时,y;
(2)将y=20代入y,
解得x=40,
即a=40;
(3)当y=40时,x20.
∴要想喝到不低于40℃的开水,x需满足8≤x≤20,
即李老师要在7:38到7:50之间接水.
23.(1)由题意可得:xy=1200×0.5,
则y,
即y关于x的函数表达式为y;
(2)∵y,
∴当x=1.5时,y400,
故当动力臂长为1.5m时,撬动石头至少需要400N的力;
(3)他不能撬动这块石头,理由如下:
∵y,
∴x,
∵0<x≤1.8,
∴01.8,
∴y≥333,
∵333300,
∴他不能撬动这块石头.
24.(1)由图象可知y与x成反比例,设y与x的函数关系式为y,
把(5,1.8)代入关系式得1.8,
∴k=9,
∴y,
∴12﹣9=3(万元).
答:首付款为3万元;
(2)当x=20时,y0.45(万元),
答:每月应付0.45万元;
(3)当y=0.4时,0.4,
解得:x,
答:他至少23个月才能结清余款.
