九年级数学上册试题 21.5反比例函数复习题-沪科版(含答案)
文档属性
| 名称 | 九年级数学上册试题 21.5反比例函数复习题-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 296.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 22:31:53 | ||
图片预览



文档简介
21.5反比例函数复习题
1.如图,一次函数y1=ax+b与反比例函数y2的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PACS△AOB时,请直接写出点P的坐标为 .
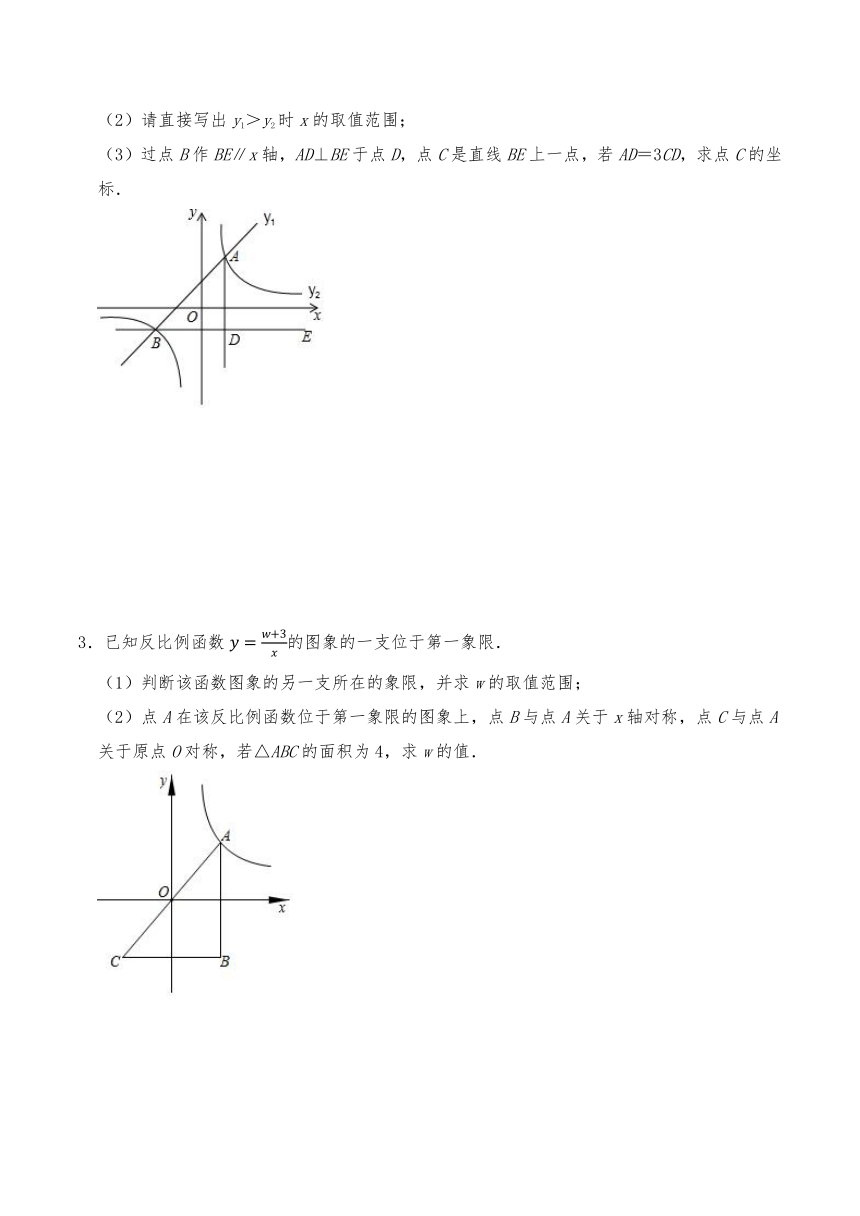
2.如图,平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2(k≠0)的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1>y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若AD=3CD,求点C的坐标.
3.已知反比例函数的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求w的取值范围;
(2)点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,若△ABC的面积为4,求w的值.
4.如图,一次函数y=kx+b(k≠0)与反比例函数y(x>0)的图象交于点A,B,与x轴交于点C,与y轴交于点D,其中点A(1,3)和点B(3,n).
(1)求一次函数的表达式.
(2)求证:BC=AD.
(3)根据图象回答:当x为何值时,kx+b0(请直接写出答案) .
5.如图,A、B是反比例函数y的图象上关于原点O对称的两点,点C是y轴负半轴上一点,直线AC与x轴交于点D,且点C是线段AD的中点,连接BD.
(1)求证:BD⊥OD;
(2)若点C的坐标是(0,﹣2),且△ABD的面积为5,求k的值和B点坐标.
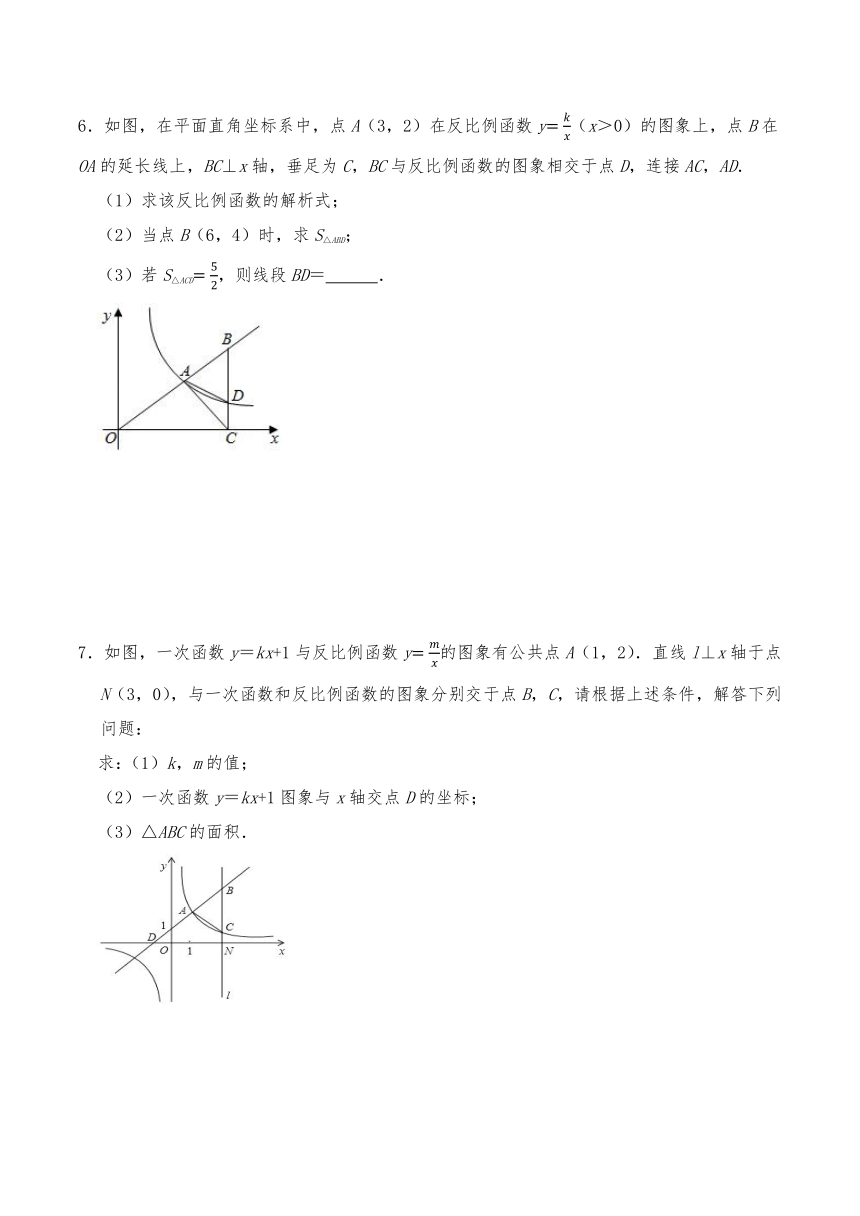
6.如图,在平面直角坐标系中,点A(3,2)在反比例函数y(x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.
(1)求该反比例函数的解析式;
(2)当点B(6,4)时,求S△ABD;
(3)若S△ACD,则线段BD= .
7.如图,一次函数y=kx+1与反比例函数y的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C,请根据上述条件,解答下列问题:
求:(1)k,m的值;
(2)一次函数y=kx+1图象与x轴交点D的坐标;
(3)△ABC的面积.
8.如图,平面直角坐标系中,直线y1=kx+b分别与x,y轴交于点A,B,与双曲线y2分别交于点C,D(点C在第一象限,点D在第三象限),作CE⊥x轴于点E,tan∠BAO,OA=4,OE=2.
(1)求反比例函数的解析式;
(2)请直接写出使y1>y2的x取值范围;
(3)在y轴上是否存在一点P,使S△ABP=S△CEP?若存在,请直接写出点P的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴、y轴上,EF垂直平分对角线AC,垂足为D.点E、点F分别在BC、OA上,连接CF、AE,反比例函数的图象恰好经过点D,交线段AE于点G,点D的坐标为(4,2).
(1)求证:四边形AECF为菱形;
(2)求直线AE的解析式;
(3)求G的坐标.
10.如图,直线AB:y=kx+b与x轴、y轴分别相交于点A(1,0)和点B(0,2),以线段AB为边在第一象限作正方形ABCD.
(1)求直线AB的解析式;
(2)求点D的坐标;
(3)若双曲线(k>0)与正方形的边CD始终有一个交点,求k的取值范围.
11.如图,一次函数yx+b的图象与y轴交于点B(0,2),与反比例函数y(x<0)的图象交于点D.以BD为对角线作矩形ABCD,使顶点A、C落在x轴上(点A在点C的右边),BD与AC交于点E.
(1)求一次函数的解析式;
(2)求点D的坐标和反比例函数的解析式;
(3)求点A的坐标.
12.如图,菱形ABCD放置在平面直角坐标系中,已知点A(﹣3,0),B(2,0),点D在y轴正半轴上,反比例函数的图象经过点C.
(1)求反比例函数的表达式.
(2)将菱形ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,求点E的坐标.
13.如图,一次函数y=2x+b的图象经过点A(﹣1,0),并与反比例函数y(x>0)的图象交于B(m,4)
(1)求k1的值;
(2)以AB为一边,在AB的左侧作正方形ABCD,求C点坐标;
(3)将正方形ABCD沿着x轴的正方向,向右平移n个单位长度,得到正方形A1B1C1D1,线段A1B1的中点为点E,若点C1和点E同时落在反比例函数y的图象上,求n的值.
14.如图,点A(1,6)和B(n,2)是一次函数y1=kx+b的图象与反比例函数y2(x>0)的图象的两个交点.
(1)求一次函数与反比例函数的表达式;
(2)设点P是y轴上的一个动点,当△PAB的周长最小时,求点P的坐标;
(3)从下面A,B两题中任选一题作答.
A.在(2)的条件下,设点D是坐标平面内一个动点,当以点A,B,P,D为顶点的四边形是平行四边形时,请直接写出符合条件的所有点D的坐标.
B.设直线AB交y轴于点C,点M是坐标平面内一个动点,点Q在y轴上运动,以点A,C,Q,M为顶点的四边形能构成菱形吗?若能,请直接写出点Q的坐标;若不能,说明理由.
15.如图,在平面直角坐标系中,一次函数y=mx+5(m≠0)的图象与反比例函数y(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的表达式.
(2)求△OAM的面积S.
(3)在y轴上求一点P,使PA+PB的值最小并求出此时点P的坐标.
16.如图,直线AB与双曲线y在第一象限内交于点P,点P的横坐标为6,直线AB与x轴、y轴分别交于A、B两点,且∠BAO=45°;
(1)求直线AB的解析式;
(2)C为线段AB上一点,过C作CD∥y轴交双曲线y于D点,连接DP,当△CDP是等腰直角三角形时,求点C的坐标.
17.如图,点A,B分别在反比例函数y(k≠0),y在第一象限的图象上,点C是y轴正半轴上一点,连接AB,OB,AC.已知四边形ABOC是平行四边形,且A,B两点的纵坐标之比为9:4.
(1)求k的值.
(2)当 ABOC是菱形时,求AB的长.
18.如图,四边形OBAC是矩形,OC=2,OB=6,反比例函数y的图象过点A.
(1)求k的值.
(2)点P为反比例图象上的一点,作PD⊥直线AC,PE⊥x轴,当四边形PDCE是正方形时,求点P的坐标.
(3)点G为坐标平面上的一点,在反比例函数的图象上是否存在一点Q,使得以A、B、Q、G为顶点组成的平行四边形面积为14?若存在,请求出点G的坐标;若不存在,请说明理由.
19.如图,在直角坐标系xOy中,矩形ABCD的DC边在x轴上,D点坐标为(﹣6,0)边AB、AD的长分别为3、8,E是BC的中点,反比例函数y的图象经过点E,与AD边交于点F.
(1)求k的值及经过A、E两点的一次函数的表达式;
(2)若x轴上有一点P,使PE+PF的值最小,试求出点P的坐标;
(3)在(2)的条件下,连接EF、PE、PF,在直线AE上找一点Q,使得S△QEF=S△PEF直接写出符合条件的Q点坐标.
20.如图,在平面直角坐标系中,反比例函数y(x>0)的图象上有一点D(m,),过点D作CD⊥x轴于点C,将点C向左平移2个单位长度得到点B,过点B作y轴的平行线交反比例函数的图象于点A,AB=4.
(1)点A的坐标为 (用含m的式子表示);
(2)求反比例函数的解析式;
(3)设直线AD的解析式为y=ax+b(a,b为常数且a≠0).则不等式(ax+b)>0的解集是 .
21.如图,一次函数y=mx+1的图象与反比例函数y的图象相交于A、B两点,点C在x轴正半轴上,点D(1,﹣2),连接OA、OD、DC、AC,四边形OACD为菱形.
(1)求一次函数与反比例函数的解析式;
(2)根据图象,直接写出反比例函数的值小于2时,x的取值范围;
(3)设点P是直线AB上一动点,且S△OAPS菱形OACD,求点P的坐标.
22.如图,一次函数y1=kx+b的图象与反比例函数y2的图象交于A(2,m),B(n,1)两点,连接OA,OB.
(1)求这个一次函数的表达式;
(2)求△OAB的面积;
(3)问:在直角坐标系中,是否存在一点P,使以O,A,B,P为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
23.如图,在平面直角坐标系中,A(6,0)、B(0,4)是矩形OACB的两个顶点,双曲线y(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y的另一个交点,
(1)点D的坐标为 ,点E的坐标为 ;
(2)动点P在第一象限内,且满足S△PBOS△ODE.
①若点P在这个反比例函数的图象上,求点P的坐标;
②连接PO、PE,当PO﹣PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
24.如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数y(k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.
(1)当m=1时,求一次函数的解析式;
(2)若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,求反比例函数的解析式.
25.如图,反比例函数y(k≠0)的图象与一次函数y=mx﹣2相交于A(6,1),B(n,﹣3),直线AB与x轴,y轴分别交于点C,D.
(1)求k,m的值;
(2)求出B点坐标,再直接写出不等式mx﹣2的解集;
(3)点M在函数y(k≠0)的图象上,点N在x轴上,若以C、D、M、N为顶点的四边形是平行四边形,请你直接写出N点坐标.
答案
1.(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2得8,解得k=16,
∴反比例函数的解析式为y;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD30,
∵S△PACS△AOB30=24,
∴2S△AOP=24,
∴2yA=24,即2OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
2.(1)把A(1,2)代入中得k=2,
∴反比例函数的表达式为,
∴B(﹣2,﹣1),
把A(1,2)和B(﹣2,﹣1)代入一次函数y1=ax+b得,
解得,
∴一次函数的表达式为y1=x+1;
(2)从图象可以看出,y1>y2时x的取值范围为﹣2<x<0或x>1;
(3)点A(1,2),点B(﹣2,﹣1),
则AD=2﹣(﹣1)=3,
由AD=3CD得CD=1,
故点C(0,﹣1)或(2,﹣1).
3.(1)∵反比例函数的图象的一支位于第一象限.
∴该函数图象的另一支所在的象限是第三象限,w+3>0,
w>﹣3,
即w的取值范围是w>﹣3;
(2)设点A的坐标为(a,b),
∵点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,
∴a>0,b>0,点B的坐标是(a,﹣b),点C的坐标是(﹣a,﹣b),
∴BC=a﹣(﹣a)=2a,AB=b+b=2b,
∵△ABC的面积为4,
∴4,
∴4,
解得:ab=2,
∵A点在反比例函数位于第一象限的图象上,
∴w+3=2,
解得:w=﹣1.
4.(1)∵点A、B在反比例函数y上,故m=1×3=3,故点B(3,1),
设直线AB的表达式为:y=kx+b,则,
解得,
故一次函数表达式为:y=﹣x+4;
(2)一次函数表达式为:y=﹣x+4,令x=0,则y=4,令y=0,则x=4,
故点C、D的坐标分别为(4,0)、(0,4),
过点A作AG⊥y轴于点G,过点B作BH⊥x轴于点H,
则AG=DG=1,BH=CH=1,
∴AD,BC,
∴BC=AD;
(3)观察函数图象知,kx+b0时,1<x<3,
故答案为:1<x<3.
5.(1)证明:∵A、B是反比例函数y的图象上关于原点O对称的两点,
∴OA=OB,
∵AC=CD,
∴BD∥OC,
∵OC⊥OD,
∴BD⊥OD.
(2)解:∵C为AD中点,C(0,﹣2),
∴A点的纵坐标为﹣4,
∵A、B关于原点O对称,
∴S△ABD=|k|=5,k=5;
又A点的纵坐标与B点的纵坐标互为相反数,
∴点B的纵坐标为4,
∴4,
∴x,
∴B(,4).
6.(1)∵点A(3,2)在反比例函数y(x>0)的图象上,
∴k=3×2=6,
∴反比例函数的解析式为y;
(2)∵点B(6,4),
∴D点的横坐标是6,
∵D在反比例函数的图象上,
∴1,
∴D(6,1),
∴BD=4﹣1=3,
∴S△ABD3×(6﹣3);
(3)过点A作AE⊥OC,垂足为E,连接AC,
设直线OA的关系式为y=kx,将A(3,2)代入得,k,
∴直线OA的关系式为yx,
设点C(a,0),把x=a代入yx,得:ya,
把x=a代入y,得:y,
∴B(a,a),即BC═a,
∴D(a,),即CD,
∵S△ACD,
∴CD EC,即(a﹣3),解得:a=18,
BD=BC﹣CDa,
故答案为:.
7.(1)将A(1,2)代入一次函数解析式得:k+1=2,
解得:k=1,
∴一次函数解析式为y=x+1;
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为y;
故k=1,m=2;
(2)由(1)知,一次函数解析式为y=x+1,
令y=0,则x+1=0,解得:x=﹣1,
故点D(﹣1,0);
(3)∵N(3,0),
∴点B横坐标为3,
将x=3代入一次函数得:y=4,将x=3代入反比例解析式得:y,
即CN,BC=4,A到BC的距离为2,
则S△ABC2.
8.(1)在Rt△AOB中,OB=OA tan∠BAO=42,
故点A、B的坐标分别为(﹣4,0)、(0,2),
将点A、B的坐标代入直线的表达式得,解得,
故直线AB的表达式为yx+2①,
当x=2时,yx+2=3,故点C(2,3),
将点C的坐标代入反比例函数表达式得:3,解得m=6,
故反比例函数的解析式y2②;
(2)联立①②并整理得:x2+4x﹣12=0,解得x=2或﹣6,
故点D(﹣6,﹣1),
观察函数图象知,y1>y2的x取值范围是x>2或﹣6<x<0;
(3)设点P的坐标为(0,t),
则S△CEPCE×OE2×3=3,
而S△ABPBP×OA|2﹣t|×4=2|2﹣t|=3,
解得t或,
故点P的坐标为(0,)或(0,).
9.(1)∵EF垂直平分对角线AC,
∴FC=FA,EA=EC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵BC∥OA,
∴∠EAC=∠FAC=∠FCA=∠ECA,
∴CF∥AE,
∴四边形AECF为平行四边形,
∵EA=EC,
∴四边形AECF为菱形;
(2)将点D的坐标代入反比例函数表达式得:2,解得k=8,
故反比例函数表达式为y①,
∵四边形AECF为菱形,
∴点D是AC的中点,
则点D是矩形OABC的中点,
故点B的坐标为(8,4),
故OC=4,OA=8,
设菱形AECF的边长为x,则AF=CF=x,OF=8﹣x,OC=4,
在Rt△OCF中,CF2=OC2+OF2,即x2=(x﹣8)2+42,
解得x=5,
则点E的坐标为(5,4),
设直线AE的表达式为y=mx+n,则,解得,
故直线AE的表达式为yx②;
(3)联立①②得:x,
解得x=4(舍去)或4,
故点G的坐标为(4,).
10.(1)将A(1,0),B(0,2)代入y=kx+b,得:
,解得:,
∴直线AB的解析式为y=﹣2x+2.
(2)作DF⊥x轴于F,则∠AFD=90°,
∵正方形ABCD,
∴BA=AD,∠BAD=90°,∠BAO+∠DAF=90°,
∵∠BAO+∠ABO=90°,
∴∠ABO=∠DAF.
在△ADF和△BAO中,,
∴△ADF≌△BAO(AAS),
∴AF=BO=2,DF=AO=1,
∴点D的坐标为(3,1).
(3)同(2)可得出点C的坐标为(2,3).
当双曲线过点D时,k=3×1=3;
当双曲线过点C时,k=2×3=6,
∴当双曲线(k>0)与正方形的边CD始终有一个交点时,k的取值范围为3≤k≤6.
11.(1)∵一次函数yx+b的图象与y轴交于点B(0,2),
∴b=2,
∴一次函数的解析式为yx+2;
(2)作DF⊥x轴于F,
∵B(0,2),
∴OB=2,
当yx+2=0时,解得x,
∴E点坐标(,0),
∴OE,
∵四边形ABCD是矩形,
∴BE=ED,
∵DF⊥x轴,BO⊥x轴,
∴∠DFE=∠BOE=90°,
∵∠DEF=∠BEO,
∴△DEF≌△BEO(AAS),
∴OB=DF=2,EF=OE,
∴OF=OE+EF=3,
∴D(﹣3,﹣2),
∵点D在反比例函数y的图象上,
∴k=6,
故y;
(3)在Rt△BOE中,BE,
在矩形ABCD中,BEBD,AEAC,BD=AC,
∴AE=BE,
∴OA=AE﹣EO1,
∴A(1,0).
12.(1)点A(﹣3,0),B(2,0),则AB=5=AD=CD=BC,
在Rt△AOD中,OA=3,AD=5,则OD=4,
故点C(5,4),
设反比例函数表达式为:y,将点C的坐标代入上式并解得:m=20,
故反比例函数表达式为:y;
(2)设菱形ABCD向上平移n个单位,则点B′、C′的坐标分别为(2,n)、(5,4+n),
将点B′的坐标代入y得,2n=20,解得:n=10,
故点B′、C′的坐标分别为(2,10)、(5,14),
则C′D′所在的直线为:y=14,
当y=14时,y14,解得:x,
故点E(,14).
13.(1)∵一次函数y=2x+b的图象经过点A(﹣1,0),
∴b=2,
∴一次函数y=2x+2,与y轴的交点E(0,2)
当y=4时,即2x+2=4,∴x=1,
∴B(1,4),
∴k1=1×4=4,
答:k1的值为:4.
(2)过点BD分别作BM⊥x轴,DN⊥x轴,垂足为M、N,过C、D分别作x轴、y轴平行线相交于点 P,
由于ABCD是正方形,易证△ABM≌△DAN≌△DCP (AAS)
∴AN=BM=CP=4,DN=DP=AM=2,
∴C(﹣3,6),
答:点C的坐标为(﹣3,6),
(3)平移前C(﹣3,6),E(0,2),沿着x轴向右平移n个单位得:C1(﹣3+n,6),E1(0+n,2),
∵点C1和点E1同时落在反比例函数y的图象上,
∴(﹣3+n)×6=2n,
∴n,
答:n的值为:.
14.(1)将点A的坐标代入反比例函数表达式得:6,
解得m=6,
故反比例函数表达式为y,
当y2时,x=3=n,即点B的坐标为(3,2),
将点A、B坐标代入一次函数表达式得:,
解得,
故一次函数表达式为y=﹣2x+8;
(2)作点A关于y轴的对称点G(﹣1,6),连接BG交y轴于点P,则点P为所求点,
理由:△PAB的周长=AP+PB+AB=GP+PB+AB=BG+AB为最小,
由点B、G的坐标,同理可得:BG的表达式为y=﹣x+5,
故点P的坐标为(0,5);
(3)能,理由:
A:由(1)(2)知,点A、B、P的坐标分别为(1,6)、(3,2)、(0,5),
设点D的坐标为(s,t),
①当AB是边时,
则点A向右平移2个单位向下平移4个单位得到B,同样点P(D)向右平移2个单位向下平移4个单位得到D(P),
则0+2=s,5﹣4=t或0﹣2=s,5+4=t,
解得或;
②当AB是对角线时,
由中点公式得:(1+3)(s+0),(6+2)(5+t),
解得;
故点D的坐标为(2,1)或(﹣2,9)或(4,3).
B:由直线AB的表达式知,点C(0,8),由点A、C的坐标知AC2=5,
设点Q的坐标为(0,m),点M的坐标为(s,t),
①当AC为边时,
则AC=CQ或AC=AQ,
即5=(m﹣8)2或5=1+(m﹣6)2,
解得m=8±或8(舍去)或4,
即m=m=8±或4;
②当AC是对角线时,
则AM=AQ且AC的中点即为MQ的中点,
则,解得,
综上,点Q的坐标为(0,8)或(0,8)或(0,4)或(0,).
15.(1)将B(4,1)代入y得:.
∴k=4.
∴y.
将B(4,1)代入y=mx+5得:1=4m+5,
∴m=﹣1.
∴y=﹣x+5.
(2)在y中,令x=1,解得y=4.
∴A(1,4).
∴S1×4=2.
(3)作点A关于y轴的对称点N,则N(﹣1,4).
连接BN交y轴于点P,点P即为所求.
设直线BN的关系式为y=kx+b,
由,得,
∴yx.
∴点P的坐标为(0,).
16.(1)∵P点在反比例函数y的图象上,
∴xy=12,
∵点P的横坐标为6,
∴y=2,
∴P(6,2),
过P作PE⊥x轴于E点,
∵∠ABO=45°,
∴∠BAO=∠ABO=∠PAE=45°,
∵P(6,2),
∴PE=AE=2,
∴A(4,0),
设直线AB的解析式为y=kx+b 且过A(4,0),P(6,2),
∴,
解得:,
∴直线AB的解析式为:y=x﹣4;
(2)要使△CDP是等腰直角三角形,只能∠DPC=90°,
设 C(m,m﹣4),则D(m,),
过P作PF⊥CD于F,则F(m,2),
∵PD=PC,PF⊥CD,
∴DF=CF,
∴2=2﹣(m﹣4),
∴m2﹣8m+12=0
(m﹣2)(m﹣6)=0
∴m1=2,m2=6(不合题意,舍去)
∴当△CDP是等腰直角三角形时,点C的坐标为(2,﹣2).
17.(1)设A点的横坐标为a,
∵四边形ABOC是平行四边形,
∴AB∥CO,
∴xA=xB=a,
∴yA,yB,
∵A,B两点的纵坐标之比为9:4,
∴9:4,
∴k=9;
(2)当 ABOC是菱形时,AB=OB,
如图,延长AB交x轴于H,
∵AB∥CO,
∴∠COH+∠OHB=180°,
∴∠OHB=90°,
设BH=4m,则AH=9m,
∴AB=AH﹣BH=5m,
在Rt△OBH中,OH3m,
∴点B的坐标为(3m,4m),
∵点B在双曲线y上,
∴3m 4m=4,
∴m(舍去负值),
∴AB=5m.
18.(1)∵OC=2,OB=6,
∴点C(2,0),点B(0,6),点A(2,6),
∵反比例函数y的图象过点A,
∴k=2×6=12;
(2)∵k=12,
∴反比例函数解析式为:y,
设点P(a,),
∵四边形PDCE是正方形,
∴PD=PE,
当点P在第一象限时,
∴a﹣2,
∴a11,a2=1(舍去)
∴点P(1,1);
当点P在第三象限,
∴2﹣a,
∴a11(舍去),a2=1,
∴点P(1,﹣1);
综上所述:点P坐标为(1,1)或(1,﹣1);
(3)设点Q坐标为(b,),
若AB为边,
∵以A、B、Q、G为顶点组成的平行四边形面积为14,
∴2×|6|=14,
∴b1=﹣12,b2,
∴点Q(﹣12,﹣1)或(,13),
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB=QG=2,AB∥QG,
∴点G(﹣10,﹣1)或(﹣14,﹣1)或(,13)或(,13);
若AB为对角线,
设点G(x,y),
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB与QG互相平分,
∴, 或,,
∴x1=14,y1=13,或x2,y2=﹣1,
∴点G(14,13)或(,﹣1),
综上所述:点G的坐标为(﹣10,﹣1)或(﹣14,﹣1)或(,13)或(,13)或(14,13)或(,﹣1).
19.(1)在矩形ABCD中,AB=3,AD=8,
∴CD=AB=3,BC=AD=8,
∵D(﹣6,0),
∴A(﹣6,8),C(﹣3,0),B(﹣3,8),
∵E是BC的中点,
∴E(﹣3,4),
∵点D在反比例函数y的图象上,
∴k=﹣3×4=﹣12,
设经过A、E两点的一次函数的表达式为y=k'x+b,
∴,
∴,
∴经过A、E两点的一次函数的表达式为yx;
(2)如图1,由(1)知,k=﹣12,
∴反比例函数的解析式为y,
∵点F的横坐标为﹣6,
∴点F的纵坐标为2,
∴F(﹣6,2),
作点F关于x轴的对称点F',则F'(﹣6,﹣2),
连接EF'交x轴于P,此时,PE+PF的值最小,
∵E(﹣3,4),
∴直线EF'的解析式为y=2x+10,
令y=0,则2x+10=0,
∴x=﹣5,
∴P(﹣5,0);
(3)如图2,
由(2)知,F'(﹣6,﹣2),
∵E(﹣3,4),F(﹣6,2),
∴S△PEF=S△EFF'﹣S△PFF'(2+2)×(﹣3+6)(2+2)×(﹣5+6)=4,
∵E(﹣3,4),F(﹣6,2),
∴直线EF的解析式为yx+6,
由(1)知,经过A、E两点的一次函数的表达式为yx,
设点Q(m,m),
过点Q作y轴的平行线交EF于G,
∴G(m,m+6),
∴QG=|mm﹣6|=|2m+6|,
∵S△QEF=S△PEF,
∴S△QEF|2m+6|×(﹣3+6)=4,
∴m或m,
∴Q(,)或(,).
20.(1)D(m,),BC=2,
∴OB=m﹣2,
又∵AB=4,AB⊥OC,
∴A(m﹣2,4),
故答案为:(m﹣2,4);
(2)反比例函数y(x>0)的图象上有A,D两点,
∴k=4×(m﹣2)m,
解得m=3,
∴k=4,
∴反比例函数的解析式为y;
(3)∵A(1,4),D(3,),
∴不等式(ax+b)>0的解集为0<x<1或x>3.
故答案为:0<x<1或x>3.
21.(1)如图,连接AD,交x轴于点E,
∵D(1,﹣2),
∴OE=1,ED=2,
∵四边形AODC是菱形,
∴AE=DE=2,EC=OE=1,
∴A(1,2),
将A(1,2)代入直线y=mx+1可得m+1=2,
解得m=1,
将A(1,2)代入反比例函数y可得2,
解得:k=2;
∴一次函数的解析式为y=x+1;反比例函数的解析式为y;
(2)∵当x=1时,反比例函数的值为2,
∴当反比例函数图象在A点下方时,对应的函数值小于2,
此时x的取值范围为:x<0或x>1;
(3)∵OC=2OE=2,AD=2DE=4,
∴S菱形OACDOC AD=4,
∵S△OAPS菱形OACD,
∴S△OAP=2,
设P点坐标为(a,a+1),AB与y轴相交于F,
则F(0,1),
∴OF=1,
∵S△OAF1×1,
当P在A的左侧时,S△FOPa OFa=S△OAP﹣S△OAF=2,
∴a=﹣3,a+1=﹣2,
∴P(﹣3,﹣2),
当P在A的右侧时,S△FOPa OFa=S△OAP+S△OAF=2,
∴a=5,a+1=6,
∴P(5,6),
综上所述,点P的坐标为(﹣3,﹣2)或(5,6).
22.(1)∵点A(2,m),B(n,1)在反比例函数y2上,
∴2m=6,n=6,
∴m=3,
∴A(2,3),B(6,1),
∵点A(2,3),B(6,1)在一次函数y1=kx+b上,
∴,
∴,
∴一次函数的表达式为y1x+4;
(2)如图1,记一次函数y1x+4的图象与x,y轴的交点为点D,C,
针对于y1x+4,
令x=0,则y1=4,
∴C(0,4),
∴OC=6,
令y1=0,则x+4=0,
∴x=8,
∴D(8,0),
∴OD=8,
过点A作AE⊥y轴于E,过点B作BF⊥x轴于F,
∵A(2,3),B(6,1),
∴AE=2,BF=1,
∴S△AOB=S△COD﹣S△AOC﹣S△BOD
OC ODOC AEOD BF
4×84×28×1
=8;
(3)存在,如图2,
当AB和OB为邻边时,点B(6,1)先向左平移6个单位再向下平移1个单位到点O(0,0),则点A也先向左平移6个单位再向下平移1个单位到点P(2﹣6,3﹣1),即P(﹣4,2);
当OA和OB为邻边时,点O(0,0)先向右平移2个单位再向上平移3个单位到点A(2,3),
则点B也先向右平移2个单位再向上平移3个单位到点P'(6+2,1+3),即P'(8,4);
当AB和OA为邻边时,点A(2,3)先向右平移4个单位再向下平移2个单位到点B(6,1),
则点O也先向右平移4个单位再向下平移2个单位到点P''(0+4,0﹣2),即P'(4,﹣2);
点P的坐标为(﹣4,2)或(4,﹣2)或(8,4).
23.(1)∵在平面直角坐标系中,A(6,0)、B(0,4)是矩形OACB的两个顶点,
∴C(6,4),
∵D是AC的中点,
∴点D的坐标为(6,2),
依题意有2,
解得k=12.
故双曲线y,
当y=4时,4,
解得x=3.
故点E的坐标为 (3,4);
(2)①设点P的横坐标为m,则
S△PBOBO m=2m,
∵S△ODE=S梯形EOAC﹣S△CDE﹣S△ODA(3+6)×43×26×2=9,
又∵S△PBOS△ODE,
∴S△PBO=8,
∴2m=8,
解得m=4,
∵点P在双曲线y上,
∴P的坐标为(4,3);
②由①知,满足S△PBOS△ODE这一条件的点P在横坐标为4的直线上,即点P在直线x=4上,
当O,P,E三点共线时,PO﹣PE的值最大,
设OE的解析式为y=k1x,
∵过点E(3,4),
∴4=3k1,
解得k1.
∴OE的解析式为yx,
当x=4时,y.
∴P的坐标为(4,);
③设P点坐标为(4,p)时,
依题意有(4﹣6)2+(p﹣4)2=42,
解得p=4±2,
4±24=±2,
则Q1(4,2),Q2(4,﹣2);
依题意有(4﹣6)2+(p﹣0)2=42,
解得p=±2(负值舍去),
Q点纵坐标为24,
Q3(4,4+2);
当P点坐标为(4,2)时,Q4(8,2).
综上所述,Q1(4,2),Q2(4,﹣2),Q3(4,4+2),Q4(8,2).
24.(1)当m=1时,点A(﹣3,1),
∵点A在反比例函数y的图象上,
∴k=﹣3×1=﹣3,
∴反比例函数的解析式为y;
∵点B(n,2)在反比例函数y图象上,
∴2n=﹣3,
∴n,
设直线AB的解析式为y=ax+b,则,
∴,
∴直线AB的解析式为yx+3;
(2)如图,过点A作AM⊥x轴于M,过点B作BN⊥x轴于N,过点A作AF⊥BN于F,交BE于G,
则四边形AMNF是矩形,
∴FN=AM,AF=MN,
∵A(﹣3,m),B(n,2),
∴BF=2﹣m,
∵AE=2﹣m,
∴BF=AE,
在△AEG和△BFG中,,
∴△AEG≌△BFG(AAS),
∴AG=BG,EG=FG,
∴BE=BG+EG=AG+FG=AF,
∵点A(﹣3,m),B(n,2)在反比例函数y的图象上,
∴k=﹣3m=2n,
∴mn,
∴BF=BN﹣FN=BN﹣AM=2﹣m=2n,MN=n﹣(﹣3)=n+3,
∴BE=AF=n+3,
∵∠AEM+∠MAE=90°,∠AEM+∠BEN=90°,
∴∠MAE=∠NEB,
∵∠AME=∠ENB=90°,
∴△AME∽△ENB,
∴,
∴MEBN,
在Rt△AME中,AM=m,AE=2﹣m,根据勾股定理得,AM2+ME2=AE2,
∴m2+()2=(2﹣m)2,
∴m,
∴k=﹣3m,
∴反比例函数的解析式为y.
25.(1)将点A(6,1)代入反比例函数y(k≠0)与一次函数y=mx﹣2中,得1,1=6m+2,
∴k=6,m;
(2)由(1)知,m,
∴直线AB的解析式为yx﹣2,
将点B(n,﹣3)代入直线yx﹣2中,得n﹣2=﹣3,
∴n=﹣2,
∴B(﹣2,﹣3),
由图象知,不等式mx﹣2的解集为0<x<6或x<﹣2;
(3)由(2)知,直线AB的解析式为yx﹣2,
当x=0时,y=﹣2,
∴D(0,﹣2),
当y=0时,x﹣2=0,
∴x=4,∴C(4,0),
由(1)知,k=6,
∴反比例函数的解析式为y,
设点M(a,),N(b,0),
∵以C、D、M、N为顶点的四边形是平行四边形,
①当CD与MN为对角线时,(0+4)(a+b),(﹣2+0)(0),
∴a=﹣3,b=7,
∴N(7,0),
②当CM与DN为对角线时,(a+4)(0+b),(0)(﹣2+0),
∴a=﹣3,b=1,
∴N(1,0),
③当CN与DM为对角线时,(b+4)(a+0),(0+0)(2),
∴a=3,b=﹣1,
∴N(﹣1,0),
即满足条件的点N的坐标为(1,0)、(7,0)、(﹣1,0);
1.如图,一次函数y1=ax+b与反比例函数y2的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PACS△AOB时,请直接写出点P的坐标为 .
2.如图,平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2(k≠0)的图象交于点A(1,2)和B(﹣2,m).
(1)求一次函数和反比例函数的表达式;
(2)请直接写出y1>y2时x的取值范围;
(3)过点B作BE∥x轴,AD⊥BE于点D,点C是直线BE上一点,若AD=3CD,求点C的坐标.
3.已知反比例函数的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求w的取值范围;
(2)点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,若△ABC的面积为4,求w的值.
4.如图,一次函数y=kx+b(k≠0)与反比例函数y(x>0)的图象交于点A,B,与x轴交于点C,与y轴交于点D,其中点A(1,3)和点B(3,n).
(1)求一次函数的表达式.
(2)求证:BC=AD.
(3)根据图象回答:当x为何值时,kx+b0(请直接写出答案) .
5.如图,A、B是反比例函数y的图象上关于原点O对称的两点,点C是y轴负半轴上一点,直线AC与x轴交于点D,且点C是线段AD的中点,连接BD.
(1)求证:BD⊥OD;
(2)若点C的坐标是(0,﹣2),且△ABD的面积为5,求k的值和B点坐标.
6.如图,在平面直角坐标系中,点A(3,2)在反比例函数y(x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.
(1)求该反比例函数的解析式;
(2)当点B(6,4)时,求S△ABD;
(3)若S△ACD,则线段BD= .
7.如图,一次函数y=kx+1与反比例函数y的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C,请根据上述条件,解答下列问题:
求:(1)k,m的值;
(2)一次函数y=kx+1图象与x轴交点D的坐标;
(3)△ABC的面积.
8.如图,平面直角坐标系中,直线y1=kx+b分别与x,y轴交于点A,B,与双曲线y2分别交于点C,D(点C在第一象限,点D在第三象限),作CE⊥x轴于点E,tan∠BAO,OA=4,OE=2.
(1)求反比例函数的解析式;
(2)请直接写出使y1>y2的x取值范围;
(3)在y轴上是否存在一点P,使S△ABP=S△CEP?若存在,请直接写出点P的坐标;若不存在,请说明理由.
9.如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴、y轴上,EF垂直平分对角线AC,垂足为D.点E、点F分别在BC、OA上,连接CF、AE,反比例函数的图象恰好经过点D,交线段AE于点G,点D的坐标为(4,2).
(1)求证:四边形AECF为菱形;
(2)求直线AE的解析式;
(3)求G的坐标.
10.如图,直线AB:y=kx+b与x轴、y轴分别相交于点A(1,0)和点B(0,2),以线段AB为边在第一象限作正方形ABCD.
(1)求直线AB的解析式;
(2)求点D的坐标;
(3)若双曲线(k>0)与正方形的边CD始终有一个交点,求k的取值范围.
11.如图,一次函数yx+b的图象与y轴交于点B(0,2),与反比例函数y(x<0)的图象交于点D.以BD为对角线作矩形ABCD,使顶点A、C落在x轴上(点A在点C的右边),BD与AC交于点E.
(1)求一次函数的解析式;
(2)求点D的坐标和反比例函数的解析式;
(3)求点A的坐标.
12.如图,菱形ABCD放置在平面直角坐标系中,已知点A(﹣3,0),B(2,0),点D在y轴正半轴上,反比例函数的图象经过点C.
(1)求反比例函数的表达式.
(2)将菱形ABCD向上平移,使点B恰好落在双曲线上,此时A,B,C,D的对应点分别为A′,B′,C′,D′,且C′D′与双曲线交于点E,求点E的坐标.
13.如图,一次函数y=2x+b的图象经过点A(﹣1,0),并与反比例函数y(x>0)的图象交于B(m,4)
(1)求k1的值;
(2)以AB为一边,在AB的左侧作正方形ABCD,求C点坐标;
(3)将正方形ABCD沿着x轴的正方向,向右平移n个单位长度,得到正方形A1B1C1D1,线段A1B1的中点为点E,若点C1和点E同时落在反比例函数y的图象上,求n的值.
14.如图,点A(1,6)和B(n,2)是一次函数y1=kx+b的图象与反比例函数y2(x>0)的图象的两个交点.
(1)求一次函数与反比例函数的表达式;
(2)设点P是y轴上的一个动点,当△PAB的周长最小时,求点P的坐标;
(3)从下面A,B两题中任选一题作答.
A.在(2)的条件下,设点D是坐标平面内一个动点,当以点A,B,P,D为顶点的四边形是平行四边形时,请直接写出符合条件的所有点D的坐标.
B.设直线AB交y轴于点C,点M是坐标平面内一个动点,点Q在y轴上运动,以点A,C,Q,M为顶点的四边形能构成菱形吗?若能,请直接写出点Q的坐标;若不能,说明理由.
15.如图,在平面直角坐标系中,一次函数y=mx+5(m≠0)的图象与反比例函数y(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的表达式.
(2)求△OAM的面积S.
(3)在y轴上求一点P,使PA+PB的值最小并求出此时点P的坐标.
16.如图,直线AB与双曲线y在第一象限内交于点P,点P的横坐标为6,直线AB与x轴、y轴分别交于A、B两点,且∠BAO=45°;
(1)求直线AB的解析式;
(2)C为线段AB上一点,过C作CD∥y轴交双曲线y于D点,连接DP,当△CDP是等腰直角三角形时,求点C的坐标.
17.如图,点A,B分别在反比例函数y(k≠0),y在第一象限的图象上,点C是y轴正半轴上一点,连接AB,OB,AC.已知四边形ABOC是平行四边形,且A,B两点的纵坐标之比为9:4.
(1)求k的值.
(2)当 ABOC是菱形时,求AB的长.
18.如图,四边形OBAC是矩形,OC=2,OB=6,反比例函数y的图象过点A.
(1)求k的值.
(2)点P为反比例图象上的一点,作PD⊥直线AC,PE⊥x轴,当四边形PDCE是正方形时,求点P的坐标.
(3)点G为坐标平面上的一点,在反比例函数的图象上是否存在一点Q,使得以A、B、Q、G为顶点组成的平行四边形面积为14?若存在,请求出点G的坐标;若不存在,请说明理由.
19.如图,在直角坐标系xOy中,矩形ABCD的DC边在x轴上,D点坐标为(﹣6,0)边AB、AD的长分别为3、8,E是BC的中点,反比例函数y的图象经过点E,与AD边交于点F.
(1)求k的值及经过A、E两点的一次函数的表达式;
(2)若x轴上有一点P,使PE+PF的值最小,试求出点P的坐标;
(3)在(2)的条件下,连接EF、PE、PF,在直线AE上找一点Q,使得S△QEF=S△PEF直接写出符合条件的Q点坐标.
20.如图,在平面直角坐标系中,反比例函数y(x>0)的图象上有一点D(m,),过点D作CD⊥x轴于点C,将点C向左平移2个单位长度得到点B,过点B作y轴的平行线交反比例函数的图象于点A,AB=4.
(1)点A的坐标为 (用含m的式子表示);
(2)求反比例函数的解析式;
(3)设直线AD的解析式为y=ax+b(a,b为常数且a≠0).则不等式(ax+b)>0的解集是 .
21.如图,一次函数y=mx+1的图象与反比例函数y的图象相交于A、B两点,点C在x轴正半轴上,点D(1,﹣2),连接OA、OD、DC、AC,四边形OACD为菱形.
(1)求一次函数与反比例函数的解析式;
(2)根据图象,直接写出反比例函数的值小于2时,x的取值范围;
(3)设点P是直线AB上一动点,且S△OAPS菱形OACD,求点P的坐标.
22.如图,一次函数y1=kx+b的图象与反比例函数y2的图象交于A(2,m),B(n,1)两点,连接OA,OB.
(1)求这个一次函数的表达式;
(2)求△OAB的面积;
(3)问:在直角坐标系中,是否存在一点P,使以O,A,B,P为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
23.如图,在平面直角坐标系中,A(6,0)、B(0,4)是矩形OACB的两个顶点,双曲线y(k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线y的另一个交点,
(1)点D的坐标为 ,点E的坐标为 ;
(2)动点P在第一象限内,且满足S△PBOS△ODE.
①若点P在这个反比例函数的图象上,求点P的坐标;
②连接PO、PE,当PO﹣PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
24.如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数y(k<0)的图象在第二象限交于A(﹣3,m),B(n,2)两点.
(1)当m=1时,求一次函数的解析式;
(2)若点E在x轴上,满足∠AEB=90°,且AE=2﹣m,求反比例函数的解析式.
25.如图,反比例函数y(k≠0)的图象与一次函数y=mx﹣2相交于A(6,1),B(n,﹣3),直线AB与x轴,y轴分别交于点C,D.
(1)求k,m的值;
(2)求出B点坐标,再直接写出不等式mx﹣2的解集;
(3)点M在函数y(k≠0)的图象上,点N在x轴上,若以C、D、M、N为顶点的四边形是平行四边形,请你直接写出N点坐标.
答案
1.(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2得8,解得k=16,
∴反比例函数的解析式为y;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD30,
∵S△PACS△AOB30=24,
∴2S△AOP=24,
∴2yA=24,即2OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
2.(1)把A(1,2)代入中得k=2,
∴反比例函数的表达式为,
∴B(﹣2,﹣1),
把A(1,2)和B(﹣2,﹣1)代入一次函数y1=ax+b得,
解得,
∴一次函数的表达式为y1=x+1;
(2)从图象可以看出,y1>y2时x的取值范围为﹣2<x<0或x>1;
(3)点A(1,2),点B(﹣2,﹣1),
则AD=2﹣(﹣1)=3,
由AD=3CD得CD=1,
故点C(0,﹣1)或(2,﹣1).
3.(1)∵反比例函数的图象的一支位于第一象限.
∴该函数图象的另一支所在的象限是第三象限,w+3>0,
w>﹣3,
即w的取值范围是w>﹣3;
(2)设点A的坐标为(a,b),
∵点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称,
∴a>0,b>0,点B的坐标是(a,﹣b),点C的坐标是(﹣a,﹣b),
∴BC=a﹣(﹣a)=2a,AB=b+b=2b,
∵△ABC的面积为4,
∴4,
∴4,
解得:ab=2,
∵A点在反比例函数位于第一象限的图象上,
∴w+3=2,
解得:w=﹣1.
4.(1)∵点A、B在反比例函数y上,故m=1×3=3,故点B(3,1),
设直线AB的表达式为:y=kx+b,则,
解得,
故一次函数表达式为:y=﹣x+4;
(2)一次函数表达式为:y=﹣x+4,令x=0,则y=4,令y=0,则x=4,
故点C、D的坐标分别为(4,0)、(0,4),
过点A作AG⊥y轴于点G,过点B作BH⊥x轴于点H,
则AG=DG=1,BH=CH=1,
∴AD,BC,
∴BC=AD;
(3)观察函数图象知,kx+b0时,1<x<3,
故答案为:1<x<3.
5.(1)证明:∵A、B是反比例函数y的图象上关于原点O对称的两点,
∴OA=OB,
∵AC=CD,
∴BD∥OC,
∵OC⊥OD,
∴BD⊥OD.
(2)解:∵C为AD中点,C(0,﹣2),
∴A点的纵坐标为﹣4,
∵A、B关于原点O对称,
∴S△ABD=|k|=5,k=5;
又A点的纵坐标与B点的纵坐标互为相反数,
∴点B的纵坐标为4,
∴4,
∴x,
∴B(,4).
6.(1)∵点A(3,2)在反比例函数y(x>0)的图象上,
∴k=3×2=6,
∴反比例函数的解析式为y;
(2)∵点B(6,4),
∴D点的横坐标是6,
∵D在反比例函数的图象上,
∴1,
∴D(6,1),
∴BD=4﹣1=3,
∴S△ABD3×(6﹣3);
(3)过点A作AE⊥OC,垂足为E,连接AC,
设直线OA的关系式为y=kx,将A(3,2)代入得,k,
∴直线OA的关系式为yx,
设点C(a,0),把x=a代入yx,得:ya,
把x=a代入y,得:y,
∴B(a,a),即BC═a,
∴D(a,),即CD,
∵S△ACD,
∴CD EC,即(a﹣3),解得:a=18,
BD=BC﹣CDa,
故答案为:.
7.(1)将A(1,2)代入一次函数解析式得:k+1=2,
解得:k=1,
∴一次函数解析式为y=x+1;
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为y;
故k=1,m=2;
(2)由(1)知,一次函数解析式为y=x+1,
令y=0,则x+1=0,解得:x=﹣1,
故点D(﹣1,0);
(3)∵N(3,0),
∴点B横坐标为3,
将x=3代入一次函数得:y=4,将x=3代入反比例解析式得:y,
即CN,BC=4,A到BC的距离为2,
则S△ABC2.
8.(1)在Rt△AOB中,OB=OA tan∠BAO=42,
故点A、B的坐标分别为(﹣4,0)、(0,2),
将点A、B的坐标代入直线的表达式得,解得,
故直线AB的表达式为yx+2①,
当x=2时,yx+2=3,故点C(2,3),
将点C的坐标代入反比例函数表达式得:3,解得m=6,
故反比例函数的解析式y2②;
(2)联立①②并整理得:x2+4x﹣12=0,解得x=2或﹣6,
故点D(﹣6,﹣1),
观察函数图象知,y1>y2的x取值范围是x>2或﹣6<x<0;
(3)设点P的坐标为(0,t),
则S△CEPCE×OE2×3=3,
而S△ABPBP×OA|2﹣t|×4=2|2﹣t|=3,
解得t或,
故点P的坐标为(0,)或(0,).
9.(1)∵EF垂直平分对角线AC,
∴FC=FA,EA=EC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵BC∥OA,
∴∠EAC=∠FAC=∠FCA=∠ECA,
∴CF∥AE,
∴四边形AECF为平行四边形,
∵EA=EC,
∴四边形AECF为菱形;
(2)将点D的坐标代入反比例函数表达式得:2,解得k=8,
故反比例函数表达式为y①,
∵四边形AECF为菱形,
∴点D是AC的中点,
则点D是矩形OABC的中点,
故点B的坐标为(8,4),
故OC=4,OA=8,
设菱形AECF的边长为x,则AF=CF=x,OF=8﹣x,OC=4,
在Rt△OCF中,CF2=OC2+OF2,即x2=(x﹣8)2+42,
解得x=5,
则点E的坐标为(5,4),
设直线AE的表达式为y=mx+n,则,解得,
故直线AE的表达式为yx②;
(3)联立①②得:x,
解得x=4(舍去)或4,
故点G的坐标为(4,).
10.(1)将A(1,0),B(0,2)代入y=kx+b,得:
,解得:,
∴直线AB的解析式为y=﹣2x+2.
(2)作DF⊥x轴于F,则∠AFD=90°,
∵正方形ABCD,
∴BA=AD,∠BAD=90°,∠BAO+∠DAF=90°,
∵∠BAO+∠ABO=90°,
∴∠ABO=∠DAF.
在△ADF和△BAO中,,
∴△ADF≌△BAO(AAS),
∴AF=BO=2,DF=AO=1,
∴点D的坐标为(3,1).
(3)同(2)可得出点C的坐标为(2,3).
当双曲线过点D时,k=3×1=3;
当双曲线过点C时,k=2×3=6,
∴当双曲线(k>0)与正方形的边CD始终有一个交点时,k的取值范围为3≤k≤6.
11.(1)∵一次函数yx+b的图象与y轴交于点B(0,2),
∴b=2,
∴一次函数的解析式为yx+2;
(2)作DF⊥x轴于F,
∵B(0,2),
∴OB=2,
当yx+2=0时,解得x,
∴E点坐标(,0),
∴OE,
∵四边形ABCD是矩形,
∴BE=ED,
∵DF⊥x轴,BO⊥x轴,
∴∠DFE=∠BOE=90°,
∵∠DEF=∠BEO,
∴△DEF≌△BEO(AAS),
∴OB=DF=2,EF=OE,
∴OF=OE+EF=3,
∴D(﹣3,﹣2),
∵点D在反比例函数y的图象上,
∴k=6,
故y;
(3)在Rt△BOE中,BE,
在矩形ABCD中,BEBD,AEAC,BD=AC,
∴AE=BE,
∴OA=AE﹣EO1,
∴A(1,0).
12.(1)点A(﹣3,0),B(2,0),则AB=5=AD=CD=BC,
在Rt△AOD中,OA=3,AD=5,则OD=4,
故点C(5,4),
设反比例函数表达式为:y,将点C的坐标代入上式并解得:m=20,
故反比例函数表达式为:y;
(2)设菱形ABCD向上平移n个单位,则点B′、C′的坐标分别为(2,n)、(5,4+n),
将点B′的坐标代入y得,2n=20,解得:n=10,
故点B′、C′的坐标分别为(2,10)、(5,14),
则C′D′所在的直线为:y=14,
当y=14时,y14,解得:x,
故点E(,14).
13.(1)∵一次函数y=2x+b的图象经过点A(﹣1,0),
∴b=2,
∴一次函数y=2x+2,与y轴的交点E(0,2)
当y=4时,即2x+2=4,∴x=1,
∴B(1,4),
∴k1=1×4=4,
答:k1的值为:4.
(2)过点BD分别作BM⊥x轴,DN⊥x轴,垂足为M、N,过C、D分别作x轴、y轴平行线相交于点 P,
由于ABCD是正方形,易证△ABM≌△DAN≌△DCP (AAS)
∴AN=BM=CP=4,DN=DP=AM=2,
∴C(﹣3,6),
答:点C的坐标为(﹣3,6),
(3)平移前C(﹣3,6),E(0,2),沿着x轴向右平移n个单位得:C1(﹣3+n,6),E1(0+n,2),
∵点C1和点E1同时落在反比例函数y的图象上,
∴(﹣3+n)×6=2n,
∴n,
答:n的值为:.
14.(1)将点A的坐标代入反比例函数表达式得:6,
解得m=6,
故反比例函数表达式为y,
当y2时,x=3=n,即点B的坐标为(3,2),
将点A、B坐标代入一次函数表达式得:,
解得,
故一次函数表达式为y=﹣2x+8;
(2)作点A关于y轴的对称点G(﹣1,6),连接BG交y轴于点P,则点P为所求点,
理由:△PAB的周长=AP+PB+AB=GP+PB+AB=BG+AB为最小,
由点B、G的坐标,同理可得:BG的表达式为y=﹣x+5,
故点P的坐标为(0,5);
(3)能,理由:
A:由(1)(2)知,点A、B、P的坐标分别为(1,6)、(3,2)、(0,5),
设点D的坐标为(s,t),
①当AB是边时,
则点A向右平移2个单位向下平移4个单位得到B,同样点P(D)向右平移2个单位向下平移4个单位得到D(P),
则0+2=s,5﹣4=t或0﹣2=s,5+4=t,
解得或;
②当AB是对角线时,
由中点公式得:(1+3)(s+0),(6+2)(5+t),
解得;
故点D的坐标为(2,1)或(﹣2,9)或(4,3).
B:由直线AB的表达式知,点C(0,8),由点A、C的坐标知AC2=5,
设点Q的坐标为(0,m),点M的坐标为(s,t),
①当AC为边时,
则AC=CQ或AC=AQ,
即5=(m﹣8)2或5=1+(m﹣6)2,
解得m=8±或8(舍去)或4,
即m=m=8±或4;
②当AC是对角线时,
则AM=AQ且AC的中点即为MQ的中点,
则,解得,
综上,点Q的坐标为(0,8)或(0,8)或(0,4)或(0,).
15.(1)将B(4,1)代入y得:.
∴k=4.
∴y.
将B(4,1)代入y=mx+5得:1=4m+5,
∴m=﹣1.
∴y=﹣x+5.
(2)在y中,令x=1,解得y=4.
∴A(1,4).
∴S1×4=2.
(3)作点A关于y轴的对称点N,则N(﹣1,4).
连接BN交y轴于点P,点P即为所求.
设直线BN的关系式为y=kx+b,
由,得,
∴yx.
∴点P的坐标为(0,).
16.(1)∵P点在反比例函数y的图象上,
∴xy=12,
∵点P的横坐标为6,
∴y=2,
∴P(6,2),
过P作PE⊥x轴于E点,
∵∠ABO=45°,
∴∠BAO=∠ABO=∠PAE=45°,
∵P(6,2),
∴PE=AE=2,
∴A(4,0),
设直线AB的解析式为y=kx+b 且过A(4,0),P(6,2),
∴,
解得:,
∴直线AB的解析式为:y=x﹣4;
(2)要使△CDP是等腰直角三角形,只能∠DPC=90°,
设 C(m,m﹣4),则D(m,),
过P作PF⊥CD于F,则F(m,2),
∵PD=PC,PF⊥CD,
∴DF=CF,
∴2=2﹣(m﹣4),
∴m2﹣8m+12=0
(m﹣2)(m﹣6)=0
∴m1=2,m2=6(不合题意,舍去)
∴当△CDP是等腰直角三角形时,点C的坐标为(2,﹣2).
17.(1)设A点的横坐标为a,
∵四边形ABOC是平行四边形,
∴AB∥CO,
∴xA=xB=a,
∴yA,yB,
∵A,B两点的纵坐标之比为9:4,
∴9:4,
∴k=9;
(2)当 ABOC是菱形时,AB=OB,
如图,延长AB交x轴于H,
∵AB∥CO,
∴∠COH+∠OHB=180°,
∴∠OHB=90°,
设BH=4m,则AH=9m,
∴AB=AH﹣BH=5m,
在Rt△OBH中,OH3m,
∴点B的坐标为(3m,4m),
∵点B在双曲线y上,
∴3m 4m=4,
∴m(舍去负值),
∴AB=5m.
18.(1)∵OC=2,OB=6,
∴点C(2,0),点B(0,6),点A(2,6),
∵反比例函数y的图象过点A,
∴k=2×6=12;
(2)∵k=12,
∴反比例函数解析式为:y,
设点P(a,),
∵四边形PDCE是正方形,
∴PD=PE,
当点P在第一象限时,
∴a﹣2,
∴a11,a2=1(舍去)
∴点P(1,1);
当点P在第三象限,
∴2﹣a,
∴a11(舍去),a2=1,
∴点P(1,﹣1);
综上所述:点P坐标为(1,1)或(1,﹣1);
(3)设点Q坐标为(b,),
若AB为边,
∵以A、B、Q、G为顶点组成的平行四边形面积为14,
∴2×|6|=14,
∴b1=﹣12,b2,
∴点Q(﹣12,﹣1)或(,13),
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB=QG=2,AB∥QG,
∴点G(﹣10,﹣1)或(﹣14,﹣1)或(,13)或(,13);
若AB为对角线,
设点G(x,y),
∵以A、B、Q、G为顶点组成的四边形是平行四边形,
∴AB与QG互相平分,
∴, 或,,
∴x1=14,y1=13,或x2,y2=﹣1,
∴点G(14,13)或(,﹣1),
综上所述:点G的坐标为(﹣10,﹣1)或(﹣14,﹣1)或(,13)或(,13)或(14,13)或(,﹣1).
19.(1)在矩形ABCD中,AB=3,AD=8,
∴CD=AB=3,BC=AD=8,
∵D(﹣6,0),
∴A(﹣6,8),C(﹣3,0),B(﹣3,8),
∵E是BC的中点,
∴E(﹣3,4),
∵点D在反比例函数y的图象上,
∴k=﹣3×4=﹣12,
设经过A、E两点的一次函数的表达式为y=k'x+b,
∴,
∴,
∴经过A、E两点的一次函数的表达式为yx;
(2)如图1,由(1)知,k=﹣12,
∴反比例函数的解析式为y,
∵点F的横坐标为﹣6,
∴点F的纵坐标为2,
∴F(﹣6,2),
作点F关于x轴的对称点F',则F'(﹣6,﹣2),
连接EF'交x轴于P,此时,PE+PF的值最小,
∵E(﹣3,4),
∴直线EF'的解析式为y=2x+10,
令y=0,则2x+10=0,
∴x=﹣5,
∴P(﹣5,0);
(3)如图2,
由(2)知,F'(﹣6,﹣2),
∵E(﹣3,4),F(﹣6,2),
∴S△PEF=S△EFF'﹣S△PFF'(2+2)×(﹣3+6)(2+2)×(﹣5+6)=4,
∵E(﹣3,4),F(﹣6,2),
∴直线EF的解析式为yx+6,
由(1)知,经过A、E两点的一次函数的表达式为yx,
设点Q(m,m),
过点Q作y轴的平行线交EF于G,
∴G(m,m+6),
∴QG=|mm﹣6|=|2m+6|,
∵S△QEF=S△PEF,
∴S△QEF|2m+6|×(﹣3+6)=4,
∴m或m,
∴Q(,)或(,).
20.(1)D(m,),BC=2,
∴OB=m﹣2,
又∵AB=4,AB⊥OC,
∴A(m﹣2,4),
故答案为:(m﹣2,4);
(2)反比例函数y(x>0)的图象上有A,D两点,
∴k=4×(m﹣2)m,
解得m=3,
∴k=4,
∴反比例函数的解析式为y;
(3)∵A(1,4),D(3,),
∴不等式(ax+b)>0的解集为0<x<1或x>3.
故答案为:0<x<1或x>3.
21.(1)如图,连接AD,交x轴于点E,
∵D(1,﹣2),
∴OE=1,ED=2,
∵四边形AODC是菱形,
∴AE=DE=2,EC=OE=1,
∴A(1,2),
将A(1,2)代入直线y=mx+1可得m+1=2,
解得m=1,
将A(1,2)代入反比例函数y可得2,
解得:k=2;
∴一次函数的解析式为y=x+1;反比例函数的解析式为y;
(2)∵当x=1时,反比例函数的值为2,
∴当反比例函数图象在A点下方时,对应的函数值小于2,
此时x的取值范围为:x<0或x>1;
(3)∵OC=2OE=2,AD=2DE=4,
∴S菱形OACDOC AD=4,
∵S△OAPS菱形OACD,
∴S△OAP=2,
设P点坐标为(a,a+1),AB与y轴相交于F,
则F(0,1),
∴OF=1,
∵S△OAF1×1,
当P在A的左侧时,S△FOPa OFa=S△OAP﹣S△OAF=2,
∴a=﹣3,a+1=﹣2,
∴P(﹣3,﹣2),
当P在A的右侧时,S△FOPa OFa=S△OAP+S△OAF=2,
∴a=5,a+1=6,
∴P(5,6),
综上所述,点P的坐标为(﹣3,﹣2)或(5,6).
22.(1)∵点A(2,m),B(n,1)在反比例函数y2上,
∴2m=6,n=6,
∴m=3,
∴A(2,3),B(6,1),
∵点A(2,3),B(6,1)在一次函数y1=kx+b上,
∴,
∴,
∴一次函数的表达式为y1x+4;
(2)如图1,记一次函数y1x+4的图象与x,y轴的交点为点D,C,
针对于y1x+4,
令x=0,则y1=4,
∴C(0,4),
∴OC=6,
令y1=0,则x+4=0,
∴x=8,
∴D(8,0),
∴OD=8,
过点A作AE⊥y轴于E,过点B作BF⊥x轴于F,
∵A(2,3),B(6,1),
∴AE=2,BF=1,
∴S△AOB=S△COD﹣S△AOC﹣S△BOD
OC ODOC AEOD BF
4×84×28×1
=8;
(3)存在,如图2,
当AB和OB为邻边时,点B(6,1)先向左平移6个单位再向下平移1个单位到点O(0,0),则点A也先向左平移6个单位再向下平移1个单位到点P(2﹣6,3﹣1),即P(﹣4,2);
当OA和OB为邻边时,点O(0,0)先向右平移2个单位再向上平移3个单位到点A(2,3),
则点B也先向右平移2个单位再向上平移3个单位到点P'(6+2,1+3),即P'(8,4);
当AB和OA为邻边时,点A(2,3)先向右平移4个单位再向下平移2个单位到点B(6,1),
则点O也先向右平移4个单位再向下平移2个单位到点P''(0+4,0﹣2),即P'(4,﹣2);
点P的坐标为(﹣4,2)或(4,﹣2)或(8,4).
23.(1)∵在平面直角坐标系中,A(6,0)、B(0,4)是矩形OACB的两个顶点,
∴C(6,4),
∵D是AC的中点,
∴点D的坐标为(6,2),
依题意有2,
解得k=12.
故双曲线y,
当y=4时,4,
解得x=3.
故点E的坐标为 (3,4);
(2)①设点P的横坐标为m,则
S△PBOBO m=2m,
∵S△ODE=S梯形EOAC﹣S△CDE﹣S△ODA(3+6)×43×26×2=9,
又∵S△PBOS△ODE,
∴S△PBO=8,
∴2m=8,
解得m=4,
∵点P在双曲线y上,
∴P的坐标为(4,3);
②由①知,满足S△PBOS△ODE这一条件的点P在横坐标为4的直线上,即点P在直线x=4上,
当O,P,E三点共线时,PO﹣PE的值最大,
设OE的解析式为y=k1x,
∵过点E(3,4),
∴4=3k1,
解得k1.
∴OE的解析式为yx,
当x=4时,y.
∴P的坐标为(4,);
③设P点坐标为(4,p)时,
依题意有(4﹣6)2+(p﹣4)2=42,
解得p=4±2,
4±24=±2,
则Q1(4,2),Q2(4,﹣2);
依题意有(4﹣6)2+(p﹣0)2=42,
解得p=±2(负值舍去),
Q点纵坐标为24,
Q3(4,4+2);
当P点坐标为(4,2)时,Q4(8,2).
综上所述,Q1(4,2),Q2(4,﹣2),Q3(4,4+2),Q4(8,2).
24.(1)当m=1时,点A(﹣3,1),
∵点A在反比例函数y的图象上,
∴k=﹣3×1=﹣3,
∴反比例函数的解析式为y;
∵点B(n,2)在反比例函数y图象上,
∴2n=﹣3,
∴n,
设直线AB的解析式为y=ax+b,则,
∴,
∴直线AB的解析式为yx+3;
(2)如图,过点A作AM⊥x轴于M,过点B作BN⊥x轴于N,过点A作AF⊥BN于F,交BE于G,
则四边形AMNF是矩形,
∴FN=AM,AF=MN,
∵A(﹣3,m),B(n,2),
∴BF=2﹣m,
∵AE=2﹣m,
∴BF=AE,
在△AEG和△BFG中,,
∴△AEG≌△BFG(AAS),
∴AG=BG,EG=FG,
∴BE=BG+EG=AG+FG=AF,
∵点A(﹣3,m),B(n,2)在反比例函数y的图象上,
∴k=﹣3m=2n,
∴mn,
∴BF=BN﹣FN=BN﹣AM=2﹣m=2n,MN=n﹣(﹣3)=n+3,
∴BE=AF=n+3,
∵∠AEM+∠MAE=90°,∠AEM+∠BEN=90°,
∴∠MAE=∠NEB,
∵∠AME=∠ENB=90°,
∴△AME∽△ENB,
∴,
∴MEBN,
在Rt△AME中,AM=m,AE=2﹣m,根据勾股定理得,AM2+ME2=AE2,
∴m2+()2=(2﹣m)2,
∴m,
∴k=﹣3m,
∴反比例函数的解析式为y.
25.(1)将点A(6,1)代入反比例函数y(k≠0)与一次函数y=mx﹣2中,得1,1=6m+2,
∴k=6,m;
(2)由(1)知,m,
∴直线AB的解析式为yx﹣2,
将点B(n,﹣3)代入直线yx﹣2中,得n﹣2=﹣3,
∴n=﹣2,
∴B(﹣2,﹣3),
由图象知,不等式mx﹣2的解集为0<x<6或x<﹣2;
(3)由(2)知,直线AB的解析式为yx﹣2,
当x=0时,y=﹣2,
∴D(0,﹣2),
当y=0时,x﹣2=0,
∴x=4,∴C(4,0),
由(1)知,k=6,
∴反比例函数的解析式为y,
设点M(a,),N(b,0),
∵以C、D、M、N为顶点的四边形是平行四边形,
①当CD与MN为对角线时,(0+4)(a+b),(﹣2+0)(0),
∴a=﹣3,b=7,
∴N(7,0),
②当CM与DN为对角线时,(a+4)(0+b),(0)(﹣2+0),
∴a=﹣3,b=1,
∴N(1,0),
③当CN与DM为对角线时,(b+4)(a+0),(0+0)(2),
∴a=3,b=﹣1,
∴N(﹣1,0),
即满足条件的点N的坐标为(1,0)、(7,0)、(﹣1,0);
