九年级数学上册试题 22.1比例线段-沪科版(含答案)
文档属性
| 名称 | 九年级数学上册试题 22.1比例线段-沪科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 22:31:24 | ||
图片预览




文档简介
22.1比例线段
第一课时
一、选择题
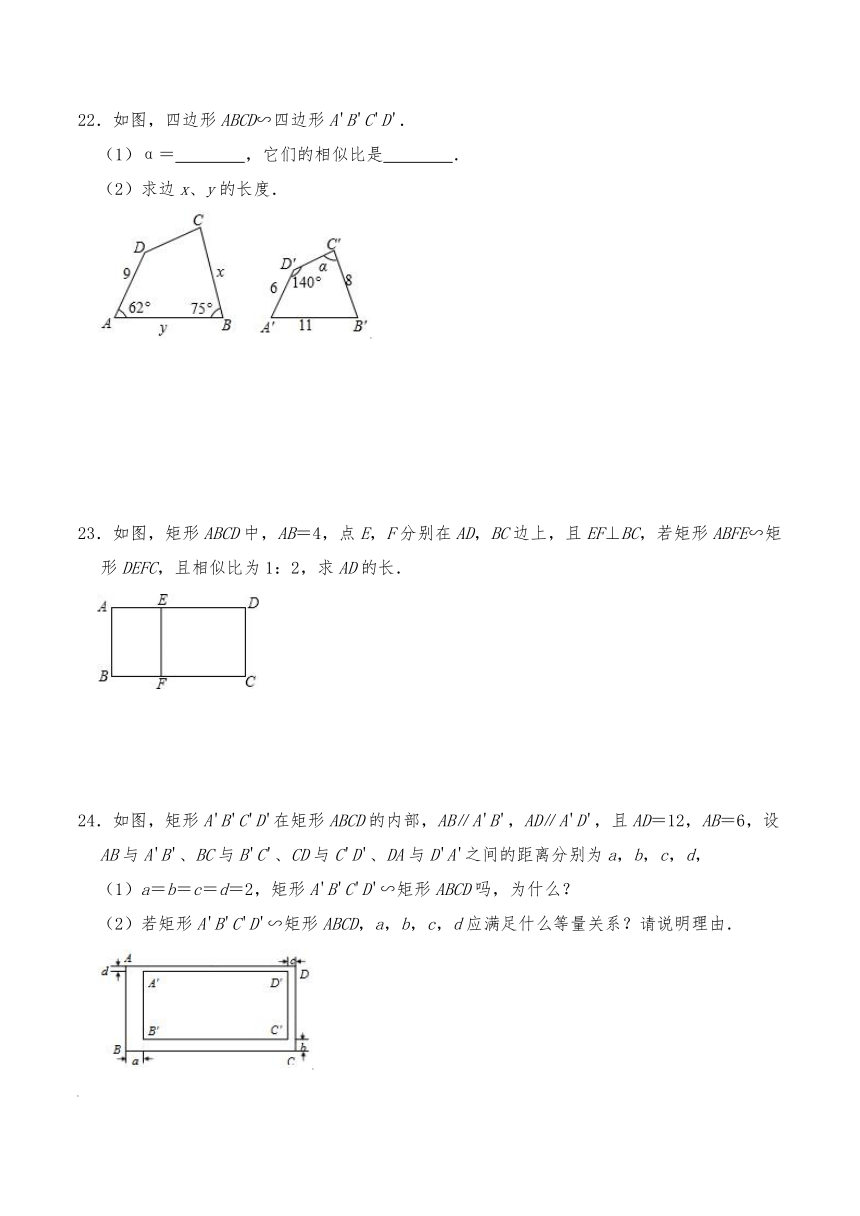
1.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A. B.
C. D.
2.观察下列每组图形,相似图形是( )
A. B.
C. D.
3.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70° B.80° C.90° D.120°
4.如图,一块矩形ABCD绸布的长AB=a,宽AD=3,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
A.3 B.2 C.3 D.2
5.如果实数a,b,c,d满足,下列四个选项中,正确的是( )
A. B. C. D.
6.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
7.已知线段a、b、c、d的长度满足等式ab=cd,如果某班四位学生分别将该等式改写成了如下四个比例式,那么其中错误的是( )
A. B. C. D.
8.已知点P、点Q是线段AB的两个黄金分割点,且AB=10,那么PQ的长为( )
A.5(3) B.10(2) C.5(1) D.5(1)
9.已知线段AB=2,P是线段AB的黄金分割点,AP>PB,那么线段AP的长度等于( )
A. B. C. D.
10.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm B.32cm C.48cm D.52cm
二、填空题
11.已知,那么的值为 .
12.如果,那么 .
13.若,且2a+b+c=33,则a﹣b+c= .
14.已知三角形的三边长为a、b、c,满足,如果其周长为36,那么该三角形的最大边长为 .
15.已知线段MN的长为4,点P是线段MN的黄金分割点,那么较长线段MP的长是 .
16.已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为 .
17.已知两个三角形是相似形,其中一个三角形的两个角分别为25°、55°,则另一个三角形的最大内角的度数为 .
18.如图,一个矩形广场的长为90m,宽为60m,广场内有两横,两纵四条小路,且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2m,那么每条纵向小路的宽为 m.
三、解答题
19.已知线段x,y满足,求的值.
20.已知0,求的值.
21.已知:a:b:c=2:3:5
(1)求代数式的值;
(2)如果3a﹣b+c=24,求a,b,c的值.
22.如图,四边形ABCD∽四边形A'B'C'D'.
(1)α= ,它们的相似比是 .
(2)求边x、y的长度.
23.如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
24.如图,矩形A'B'C'D'在矩形ABCD的内部,AB∥A'B',AD∥A'D',且AD=12,AB=6,设AB与A'B'、BC与B'C'、CD与C'D'、DA与D'A'之间的距离分别为a,b,c,d,
(1)a=b=c=d=2,矩形A'B'C'D'∽矩形ABCD吗,为什么?
(2)若矩形A'B'C'D'∽矩形ABCD,a,b,c,d应满足什么等量关系?请说明理由.
第二课时
一、选择题
1.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2 B. C.1 D.
2.如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=3CE,AB=8,则AD的长为( )
A.3 B.4 C.5 D.6
3.如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
4.如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
A. B. C. D.
5.如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A. B. C. D.
6.已知△ABC中,D、E分别是边AB、AC上的点,下列各式中,不能判断DE∥BC的是( )
A. B. C. D.
7.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么下列结论正确的是( )
A.DF B.EF C.CD D.BF
8.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
A. B. C. D.
9.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A. B. C. D.
10.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,过点B的直线DE分别交l1,l3于点D,E.若AB=2,BC=4,BD=3,则线段BE的长为( )
A.4 B.5 C.6 D.9
二、填空题
11.如图,直线l1∥l2∥l3,直线AF分别交l1,l2,l3于点A,D,F,直线BE分别交l1,l2,l3于点B,C,E,两直线AF,BE相交于点O.若AD=DF,OA=OD,则 .
12.如图,AC∥EF∥BD,若AE:EB=2:3,CD=10,则CF= .
13.如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 .
14.如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=4,AC=6,DF=10,则DE= .
15.如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为 .
16.如图,在梯形ABCD中,AD∥BC.点E、F、G在边AB上,点H、I、J在边CD上,且AE=EF=FG=GB,DH=HI=IJ=JC.如果AD=2,GJ=5,那么BC= .
17.如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1,且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1= m.
18.如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF= .
三、解答题
19.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
20.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
21.如图,已知在△ABC中,EF∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)当AB时,求证:DE∥BC.
22.如图,已知AD∥BE∥CF,如果AB=3,AC=7,EF=6.
(1)求DE的长.
(2)如果AC与DF相交于点O,OF=1,求.
23.如图,l1∥l2∥l3,ABAC,DF=9,求EF的长.
24.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
第一课时答案
一、选择题
B.C.B.C.A.B.A.B.B.C.
二.填空题
11.﹣3. 12.. 13.9. 14.16. 15.22.
16.2:1或1:2或1:1. 17.100°. 18.1.8.
三.解答题
19.∵,
∴y(2x+y)=x(x﹣y),
则x2﹣3xy﹣y2=0,
解得x1y,x2y(负值舍去).
故的值为.
20.设k≠0,则a=2k,b=3k,c=5k,
则.
21.(1)∵a:b:c=2:3:5,
∴设a=2k,b=3k,c=5k(k≠0),
则1;
设a=2k,b=3k,c=5k(k≠0),则
6k﹣3k+5k=24,
解得k=3.
则a=2k=6,
b=3k=9,
c=5k=15.
22.(1)∵四边形ABCD∽四边形A'B'C'D',
∴∠A′=∠A=62°,∠B′=∠B=75°,
∴∠C′=360°﹣62°﹣75°﹣140°=83°,
它们的相似比为:,
故答案为:83°;;
(2)∵四边形ABCD∽四边形A'B'C'D',
∴,
解得,x=12,y.
23.∵矩形ABFE∽矩形DEFC,且相似比为1:2,
∴,
∵四边形ABCD为矩形,
∴CD=AB=4
∴,
∴DE=8,AE=2,
∴AD=AE+DE=2+8=10.
24.(1)不相似,理由如下:
∵,
∴不相似;
(2)要使矩形A′B′C′D′∽矩形ABCD,
就要,即
可得:2d+2b=a+c.
第二课时答案
一、选择题
B.D.D.B A.B.D.C.A.C.
二、填空题
11..12.4. 13.15.14.. 15.9.16.6.
17.1.2.18.7.2.
三、解答题
19.(1)∵AD∥BE∥CF,
∴;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NE∥MF,
∴,
∴NEMF14=6,
∴BE=BN+NE=5+6=11
20.(1)∵FE∥CD,
∴,即
解得,AC,
则CE=AC﹣AE4
(2)∵DE∥BC,
∴,即,
解得,AB.
21.(1)∵EF∥CD,
∴,
∵AF=3,AD=5,AE=4,
∴,
解得:AC,
∵AE=4,
∴CE=AC﹣AE4
(2)∵AB,AD=5,AE=4,AC,
∴,
∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.
22.(1)∵AD∥BE∥CF,
∴,即,
∴DE;
(2)∵OF=1,
∴OE=6﹣1=5,
∴OD=5,
∵AD∥CF,
∴.
23.∵ABAC,
∴,
∴,
∵l1∥l2∥l3,
∴,
∵DF=9,
∴,
解得:EF.
24.(1)∵AD平分∠BAC,∠BAC=60°,
∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,
∴CD=2,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,
∴BC=6,
∴BD=BC﹣CD=4,
∵DE∥CA,
∴,
∴DE=4;
(2)如图,
∵点M是线段AD的中点,
∴DM=AM,
∵DE∥CA,
∴,
∴DF=AG,
∵DE∥CA,
∴,
∴,
∵BD=4,BC=6,DF=AG,
∴.
第一课时
一、选择题
1.下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )
A. B.
C. D.
2.观察下列每组图形,相似图形是( )
A. B.
C. D.
3.如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠E的度数为( )
A.70° B.80° C.90° D.120°
4.如图,一块矩形ABCD绸布的长AB=a,宽AD=3,按照图中的方式将它裁成相同的三面矩形彩旗,如果裁出的每面彩旗与矩形ABCD绸布相似,则a的值等于( )
A.3 B.2 C.3 D.2
5.如果实数a,b,c,d满足,下列四个选项中,正确的是( )
A. B. C. D.
6.A、B两地的实际距离AB=250米,如果画在地图上的距离A′B′=5厘米,那么地图上的距离与实际距离的比为( )
A.1:500 B.1:5000 C.500:1 D.5000:1
7.已知线段a、b、c、d的长度满足等式ab=cd,如果某班四位学生分别将该等式改写成了如下四个比例式,那么其中错误的是( )
A. B. C. D.
8.已知点P、点Q是线段AB的两个黄金分割点,且AB=10,那么PQ的长为( )
A.5(3) B.10(2) C.5(1) D.5(1)
9.已知线段AB=2,P是线段AB的黄金分割点,AP>PB,那么线段AP的长度等于( )
A. B. C. D.
10.两个相似多边形的一组对应边分别是3cm和4.5cm,如果它们的周长之和是80cm,那么较大的多边形的周长是( )
A.16cm B.32cm C.48cm D.52cm
二、填空题
11.已知,那么的值为 .
12.如果,那么 .
13.若,且2a+b+c=33,则a﹣b+c= .
14.已知三角形的三边长为a、b、c,满足,如果其周长为36,那么该三角形的最大边长为 .
15.已知线段MN的长为4,点P是线段MN的黄金分割点,那么较长线段MP的长是 .
16.已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为 .
17.已知两个三角形是相似形,其中一个三角形的两个角分别为25°、55°,则另一个三角形的最大内角的度数为 .
18.如图,一个矩形广场的长为90m,宽为60m,广场内有两横,两纵四条小路,且小路内外边缘所围成的两个矩形相似,如果两条横向小路的宽均为1.2m,那么每条纵向小路的宽为 m.
三、解答题
19.已知线段x,y满足,求的值.
20.已知0,求的值.
21.已知:a:b:c=2:3:5
(1)求代数式的值;
(2)如果3a﹣b+c=24,求a,b,c的值.
22.如图,四边形ABCD∽四边形A'B'C'D'.
(1)α= ,它们的相似比是 .
(2)求边x、y的长度.
23.如图,矩形ABCD中,AB=4,点E,F分别在AD,BC边上,且EF⊥BC,若矩形ABFE∽矩形DEFC,且相似比为1:2,求AD的长.
24.如图,矩形A'B'C'D'在矩形ABCD的内部,AB∥A'B',AD∥A'D',且AD=12,AB=6,设AB与A'B'、BC与B'C'、CD与C'D'、DA与D'A'之间的距离分别为a,b,c,d,
(1)a=b=c=d=2,矩形A'B'C'D'∽矩形ABCD吗,为什么?
(2)若矩形A'B'C'D'∽矩形ABCD,a,b,c,d应满足什么等量关系?请说明理由.
第二课时
一、选择题
1.如图,直线l1∥l2∥l3,直线AC和DF被l1,l2,l3所截,如果AB=2,BC=3,EF=2,那么DE的长是( )
A.2 B. C.1 D.
2.如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=3CE,AB=8,则AD的长为( )
A.3 B.4 C.5 D.6
3.如图,在△ABC中,DE∥AB,且,则的值为( )
A. B. C. D.
4.如图,已知点E、F分别是△ABC的边AB、AC上的点,且EF∥BC,点D是BC边上的点,AD与EF交于点H,则下列结论中,错误的是( )
A. B. C. D.
5.如图,点D、E分别在△ABC的边AB、BC上,下列条件中,不能判定DE∥AC的条件是( )
A. B. C. D.
6.已知△ABC中,D、E分别是边AB、AC上的点,下列各式中,不能判断DE∥BC的是( )
A. B. C. D.
7.如图,AB∥CD∥EF,AC=2,AE=5,BD=1.5,那么下列结论正确的是( )
A.DF B.EF C.CD D.BF
8.如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是( )
A. B. C. D.
9.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A. B. C. D.
10.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,过点B的直线DE分别交l1,l3于点D,E.若AB=2,BC=4,BD=3,则线段BE的长为( )
A.4 B.5 C.6 D.9
二、填空题
11.如图,直线l1∥l2∥l3,直线AF分别交l1,l2,l3于点A,D,F,直线BE分别交l1,l2,l3于点B,C,E,两直线AF,BE相交于点O.若AD=DF,OA=OD,则 .
12.如图,AC∥EF∥BD,若AE:EB=2:3,CD=10,则CF= .
13.如图,已知AC∥EF∥BD.如果AE:EB=2:3,CF=6.那么CD的长等于 .
14.如图,已知直线l1、l2、l3分别交直线l4于点A、B、C,交直线l5于点D、E、F,且l1∥l2∥l3,AB=4,AC=6,DF=10,则DE= .
15.如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为 .
16.如图,在梯形ABCD中,AD∥BC.点E、F、G在边AB上,点H、I、J在边CD上,且AE=EF=FG=GB,DH=HI=IJ=JC.如果AD=2,GJ=5,那么BC= .
17.如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1,且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1= m.
18.如图,a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB=6,BC=9,DF=12,则EF= .
三、解答题
19.如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,且AB=6,BC=8.
(1)求的值;
(2)当AD=5,CF=19时,求BE的长.
20.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)求AB的长.
21.如图,已知在△ABC中,EF∥CD,AF=3,AD=5,AE=4.
(1)求CE的长;
(2)当AB时,求证:DE∥BC.
22.如图,已知AD∥BE∥CF,如果AB=3,AC=7,EF=6.
(1)求DE的长.
(2)如果AC与DF相交于点O,OF=1,求.
23.如图,l1∥l2∥l3,ABAC,DF=9,求EF的长.
24.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.
(1)求线段DE的长;
(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.
第一课时答案
一、选择题
B.C.B.C.A.B.A.B.B.C.
二.填空题
11.﹣3. 12.. 13.9. 14.16. 15.22.
16.2:1或1:2或1:1. 17.100°. 18.1.8.
三.解答题
19.∵,
∴y(2x+y)=x(x﹣y),
则x2﹣3xy﹣y2=0,
解得x1y,x2y(负值舍去).
故的值为.
20.设k≠0,则a=2k,b=3k,c=5k,
则.
21.(1)∵a:b:c=2:3:5,
∴设a=2k,b=3k,c=5k(k≠0),
则1;
设a=2k,b=3k,c=5k(k≠0),则
6k﹣3k+5k=24,
解得k=3.
则a=2k=6,
b=3k=9,
c=5k=15.
22.(1)∵四边形ABCD∽四边形A'B'C'D',
∴∠A′=∠A=62°,∠B′=∠B=75°,
∴∠C′=360°﹣62°﹣75°﹣140°=83°,
它们的相似比为:,
故答案为:83°;;
(2)∵四边形ABCD∽四边形A'B'C'D',
∴,
解得,x=12,y.
23.∵矩形ABFE∽矩形DEFC,且相似比为1:2,
∴,
∵四边形ABCD为矩形,
∴CD=AB=4
∴,
∴DE=8,AE=2,
∴AD=AE+DE=2+8=10.
24.(1)不相似,理由如下:
∵,
∴不相似;
(2)要使矩形A′B′C′D′∽矩形ABCD,
就要,即
可得:2d+2b=a+c.
第二课时答案
一、选择题
B.D.D.B A.B.D.C.A.C.
二、填空题
11..12.4. 13.15.14.. 15.9.16.6.
17.1.2.18.7.2.
三、解答题
19.(1)∵AD∥BE∥CF,
∴;
(2)过D点作DM∥AC交CF于M,交BE于N,如图,
∵AD∥BN∥CM,AC∥DM,
∴四边形ABND和四边形ACMD都是平行四边形,
∴BN=AD=5,CM=AD=5,
∴MF=CF﹣CM=19﹣5=14,
∵NE∥MF,
∴,
∴NEMF14=6,
∴BE=BN+NE=5+6=11
20.(1)∵FE∥CD,
∴,即
解得,AC,
则CE=AC﹣AE4
(2)∵DE∥BC,
∴,即,
解得,AB.
21.(1)∵EF∥CD,
∴,
∵AF=3,AD=5,AE=4,
∴,
解得:AC,
∵AE=4,
∴CE=AC﹣AE4
(2)∵AB,AD=5,AE=4,AC,
∴,
∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠B,
∴DE∥BC.
22.(1)∵AD∥BE∥CF,
∴,即,
∴DE;
(2)∵OF=1,
∴OE=6﹣1=5,
∴OD=5,
∵AD∥CF,
∴.
23.∵ABAC,
∴,
∴,
∵l1∥l2∥l3,
∴,
∵DF=9,
∴,
解得:EF.
24.(1)∵AD平分∠BAC,∠BAC=60°,
∴∠DAC=30°,
在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,
∴CD=2,
在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,
∴BC=6,
∴BD=BC﹣CD=4,
∵DE∥CA,
∴,
∴DE=4;
(2)如图,
∵点M是线段AD的中点,
∴DM=AM,
∵DE∥CA,
∴,
∴DF=AG,
∵DE∥CA,
∴,
∴,
∵BD=4,BC=6,DF=AG,
∴.
