九年级数学上册试题 第23章《解直角三角形》单元测试 -沪科版(含答案)
文档属性
| 名称 | 九年级数学上册试题 第23章《解直角三角形》单元测试 -沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 22:34:09 | ||
图片预览



文档简介
第23章《解直角三角形》单元测试
一、选择题(本大题共10小题,每小题3分,共30分)
1.在中,,那么锐角的正弦等于
A. B.
C. D.
2.在中,,若,,则的值为
A. B. C. D.
3.在中,,,,那么的度数是
A. B. C. D.
4.如图,已知,,,,则下列结论正确的是
A. B. C. D.
5.如图,热气球的探测器显示,从热气球处看一栋楼顶部处的仰角为,看这栋楼底部处的俯角为,热气球处与楼的水平距离为,则这栋楼的高度为
A. B. C. D.
6.如图,的三个顶点均在格点上,则的值为
A. B. C.2 D.
7.如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点处测得旗杆顶端的仰角为,测角仪的高度为1米,其底端与旗杆底端之间的距离为6米,设旗杆的高度为米,则下列关系式正确的是
A. B. C. D.
8.如图,在中,,为的中点,点在上,,交于点,,,则的值为
A. B. C. D.
9.如图,在等腰直角三角形中,,,是上一点,若,则的长为
A. B. C. D.8
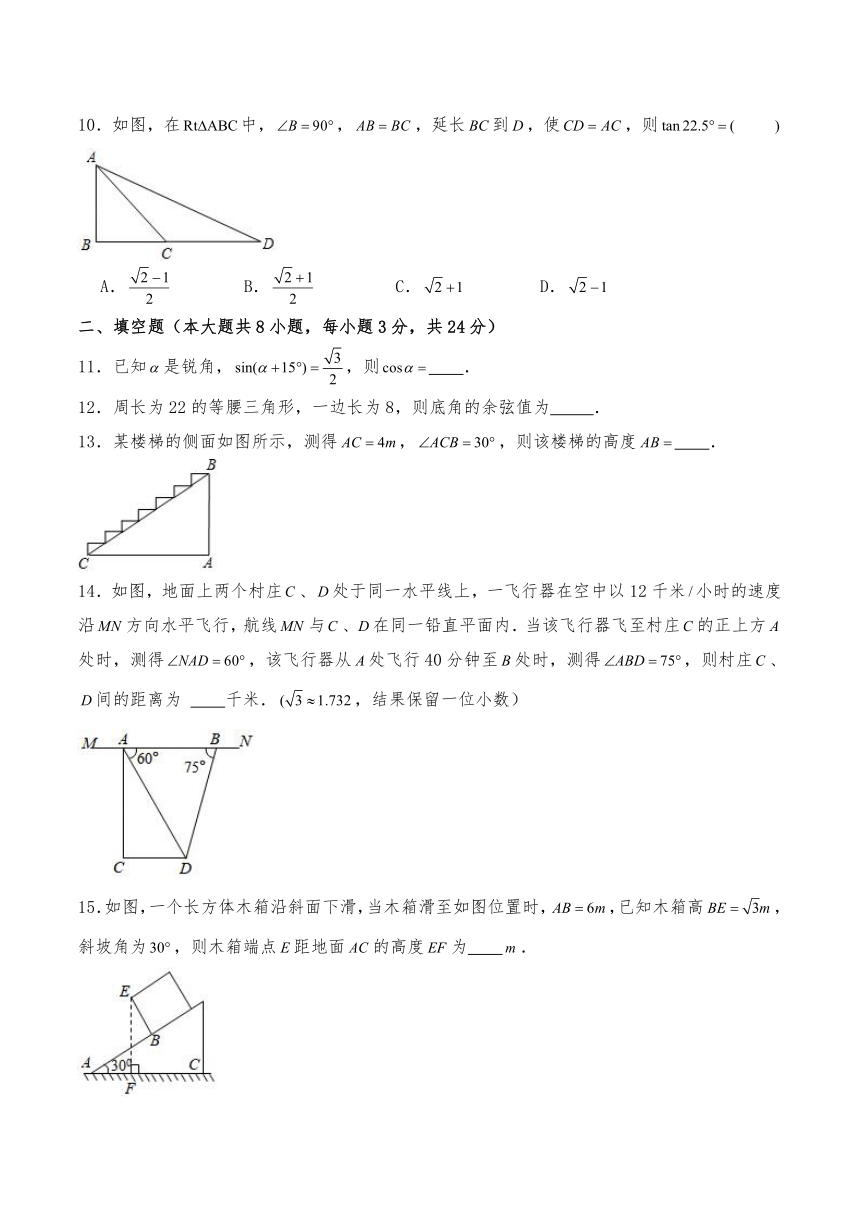
10.如图,在中,,,延长到,使,则
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知是锐角,,则 .
12.周长为22的等腰三角形,一边长为8,则底角的余弦值为 .
13.某楼梯的侧面如图所示,测得,,则该楼梯的高度 .
14.如图,地面上两个村庄、处于同一水平线上,一飞行器在空中以12千米小时的速度沿方向水平飞行,航线与、在同一铅直平面内.当该飞行器飞至村庄的正上方处时,测得,该飞行器从处飞行40分钟至处时,测得,则村庄、间的距离为 千米.,结果保留一位小数)
15.如图,一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜坡角为,则木箱端点距地面的高度为 .
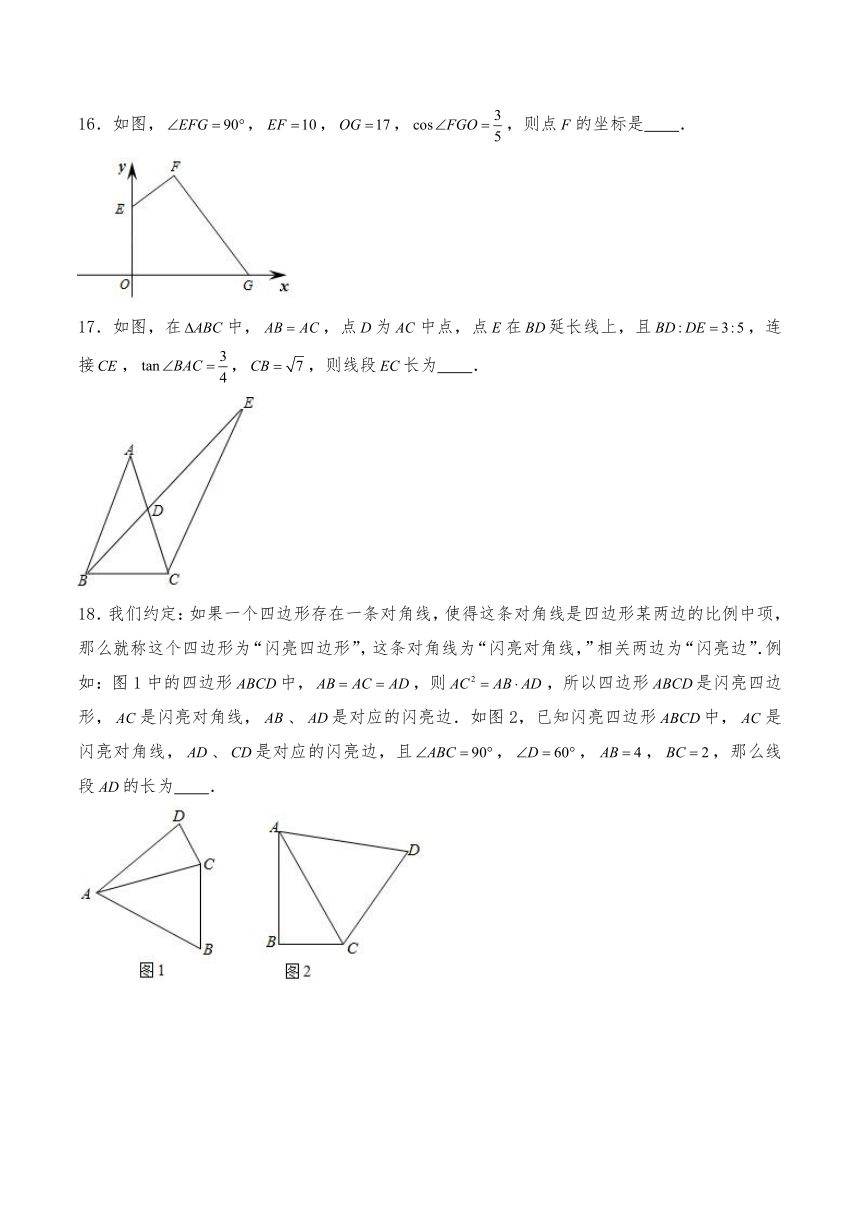
16.如图,,,,,则点的坐标是 .
17.如图,在中,,点为中点,点在延长线上,且,连接,,,则线段长为 .
18.我们约定:如果一个四边形存在一条对角线,使得这条对角线是四边形某两边的比例中项,那么就称这个四边形为“闪亮四边形”,这条对角线为“闪亮对角线,”相关两边为“闪亮边”.例如:图1中的四边形中,,则,所以四边形是闪亮四边形,是闪亮对角线,、是对应的闪亮边.如图2,已知闪亮四边形中,是闪亮对角线,、是对应的闪亮边,且,,,,那么线段的长为 .
三、解答题(本大题共8小题,共66分.)
19.(1)已知中,,,,解直角三角形.
(2)已知中,,,,求的长.
20.如图,在中,,,的平分线交于点,,求的长?
21.某次台风来袭时,一棵笔直大树树干(假定树干垂直于水平地面)被刮倾斜(即后折断倒在地上,树的顶部恰好接触到地面处,测得,米,求这棵大树的高度.(结果保留根号)(参考数据:,,
22.如图,小亮在大楼的观光电梯中的点测得大楼楼底点的俯角为,此时他距地面的高度为21米,电梯再上升9米到达点,此时测得大楼楼顶点的仰角为,求大楼的高度.(结果保留根号)
23.如图①,一台灯放置在水平桌面上,底座与桌面垂直,底座高,连杆,,与始终在同一平面内.
(1)如图②,转动连杆,,使成平角,,求连杆端点离桌面的高度.
(2)将图②中的连杆再绕点逆时针旋转,如图③,此时连杆端点离桌面的高度减小了 .
(参考数据:,,
24.图1是一台实物投影仪,图2是它的示意图,折线表示支架,支架的一部分是固定的,另一部分是可旋转的,线段表示投影探头,表示水平桌面,,垂足为点,且,,,.
将图2中的绕点向下旋转,使得落在的位置(如图3所示),此时,,,求点到水平桌面的距离,(参考数据:,,,结果精确到
25.如图1.点、在直线上在的左侧),点是直线上方一点.若,,记,为的双角坐标.例如,若是等边三角形,则点的双角坐标为,.
(1)如图2,若,,,求的面积;
(参考数据:,.
(2)在图3中用直尺和圆规作出点,,其中且.(保留作图痕迹)
26.已知,,,是边上一点,连接,是上一点,且.
(1)如图1,若,
①求证:平分;
②求的值;
(2)如图2,连接,若,求的值.
答案
一、选择题
..........
二、填空题
11.. 12.或. 13. 14.5.5.
15.. 16.. 17.. 18..
三、解答题
19.(1)在中,,,,
,
,
,
,
,
,,;
(2)如图1,过点作,垂足为,
,,
,
在中,
,
,
如图2,,
故的长为或.
20.在中,,,
,
,
是的平分线,
,
又,
,
在中,,,
.
答:的长为6.
21.过点作于点,则.
在中,,
,
,
,
.
在中,
,
,
,
(米.
答:这棵大树原来的高度是米.
22.过作于,过作于.
由已知得,,,米,米.
在中,米,,
(米.
米.
在中,,
米.
米.
答:大楼的高度是米.
23.(1)作于点,则,
,,
.
四边形为矩形.
,,
,
,
,
,
在中,,
,
,
,
,
答:连杆端点离桌面的高度为;
(2)如图3,作于,于,于,于.则四边形是矩形,
,,
,
,,
,,
,
下降高度:.
故答案为:4.
24.过作于,
过作于,延长交于,
则,,
设,
,
,
,
,
,
,
,
解得:,
,
,
答:到水平桌面的距离为.
25.(1)过点作于点,则,
在中,,
,
,
在中,,
,
,
,
,
解得,
;
(2)如图3,点即为所求.
26.(1)①证明:,
,
,
,,
,
,
,
,
,,
,
,
平分.
②解:如图1中,过点作于.
平分,,,
,
,,
,
,
.
(2)解:如图2中,连接,过点作交的延长线于.
,,
,
,,
,
,
,
,,
,,
,
,
一、选择题(本大题共10小题,每小题3分,共30分)
1.在中,,那么锐角的正弦等于
A. B.
C. D.
2.在中,,若,,则的值为
A. B. C. D.
3.在中,,,,那么的度数是
A. B. C. D.
4.如图,已知,,,,则下列结论正确的是
A. B. C. D.
5.如图,热气球的探测器显示,从热气球处看一栋楼顶部处的仰角为,看这栋楼底部处的俯角为,热气球处与楼的水平距离为,则这栋楼的高度为
A. B. C. D.
6.如图,的三个顶点均在格点上,则的值为
A. B. C.2 D.
7.如图,数学活动小组利用测角仪和皮尺测量学校旗杆的高度,在点处测得旗杆顶端的仰角为,测角仪的高度为1米,其底端与旗杆底端之间的距离为6米,设旗杆的高度为米,则下列关系式正确的是
A. B. C. D.
8.如图,在中,,为的中点,点在上,,交于点,,,则的值为
A. B. C. D.
9.如图,在等腰直角三角形中,,,是上一点,若,则的长为
A. B. C. D.8
10.如图,在中,,,延长到,使,则
A. B. C. D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.已知是锐角,,则 .
12.周长为22的等腰三角形,一边长为8,则底角的余弦值为 .
13.某楼梯的侧面如图所示,测得,,则该楼梯的高度 .
14.如图,地面上两个村庄、处于同一水平线上,一飞行器在空中以12千米小时的速度沿方向水平飞行,航线与、在同一铅直平面内.当该飞行器飞至村庄的正上方处时,测得,该飞行器从处飞行40分钟至处时,测得,则村庄、间的距离为 千米.,结果保留一位小数)
15.如图,一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜坡角为,则木箱端点距地面的高度为 .
16.如图,,,,,则点的坐标是 .
17.如图,在中,,点为中点,点在延长线上,且,连接,,,则线段长为 .
18.我们约定:如果一个四边形存在一条对角线,使得这条对角线是四边形某两边的比例中项,那么就称这个四边形为“闪亮四边形”,这条对角线为“闪亮对角线,”相关两边为“闪亮边”.例如:图1中的四边形中,,则,所以四边形是闪亮四边形,是闪亮对角线,、是对应的闪亮边.如图2,已知闪亮四边形中,是闪亮对角线,、是对应的闪亮边,且,,,,那么线段的长为 .
三、解答题(本大题共8小题,共66分.)
19.(1)已知中,,,,解直角三角形.
(2)已知中,,,,求的长.
20.如图,在中,,,的平分线交于点,,求的长?
21.某次台风来袭时,一棵笔直大树树干(假定树干垂直于水平地面)被刮倾斜(即后折断倒在地上,树的顶部恰好接触到地面处,测得,米,求这棵大树的高度.(结果保留根号)(参考数据:,,
22.如图,小亮在大楼的观光电梯中的点测得大楼楼底点的俯角为,此时他距地面的高度为21米,电梯再上升9米到达点,此时测得大楼楼顶点的仰角为,求大楼的高度.(结果保留根号)
23.如图①,一台灯放置在水平桌面上,底座与桌面垂直,底座高,连杆,,与始终在同一平面内.
(1)如图②,转动连杆,,使成平角,,求连杆端点离桌面的高度.
(2)将图②中的连杆再绕点逆时针旋转,如图③,此时连杆端点离桌面的高度减小了 .
(参考数据:,,
24.图1是一台实物投影仪,图2是它的示意图,折线表示支架,支架的一部分是固定的,另一部分是可旋转的,线段表示投影探头,表示水平桌面,,垂足为点,且,,,.
将图2中的绕点向下旋转,使得落在的位置(如图3所示),此时,,,求点到水平桌面的距离,(参考数据:,,,结果精确到
25.如图1.点、在直线上在的左侧),点是直线上方一点.若,,记,为的双角坐标.例如,若是等边三角形,则点的双角坐标为,.
(1)如图2,若,,,求的面积;
(参考数据:,.
(2)在图3中用直尺和圆规作出点,,其中且.(保留作图痕迹)
26.已知,,,是边上一点,连接,是上一点,且.
(1)如图1,若,
①求证:平分;
②求的值;
(2)如图2,连接,若,求的值.
答案
一、选择题
..........
二、填空题
11.. 12.或. 13. 14.5.5.
15.. 16.. 17.. 18..
三、解答题
19.(1)在中,,,,
,
,
,
,
,
,,;
(2)如图1,过点作,垂足为,
,,
,
在中,
,
,
如图2,,
故的长为或.
20.在中,,,
,
,
是的平分线,
,
又,
,
在中,,,
.
答:的长为6.
21.过点作于点,则.
在中,,
,
,
,
.
在中,
,
,
,
(米.
答:这棵大树原来的高度是米.
22.过作于,过作于.
由已知得,,,米,米.
在中,米,,
(米.
米.
在中,,
米.
米.
答:大楼的高度是米.
23.(1)作于点,则,
,,
.
四边形为矩形.
,,
,
,
,
,
在中,,
,
,
,
,
答:连杆端点离桌面的高度为;
(2)如图3,作于,于,于,于.则四边形是矩形,
,,
,
,,
,,
,
下降高度:.
故答案为:4.
24.过作于,
过作于,延长交于,
则,,
设,
,
,
,
,
,
,
,
解得:,
,
,
答:到水平桌面的距离为.
25.(1)过点作于点,则,
在中,,
,
,
在中,,
,
,
,
,
解得,
;
(2)如图3,点即为所求.
26.(1)①证明:,
,
,
,,
,
,
,
,
,,
,
,
平分.
②解:如图1中,过点作于.
平分,,,
,
,,
,
,
.
(2)解:如图2中,连接,过点作交的延长线于.
,,
,
,,
,
,
,
,,
,,
,
,
