七年级数学下册试题 10.4 平移-沪科版(含答案)
文档属性
| 名称 | 七年级数学下册试题 10.4 平移-沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 159.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 22:36:20 | ||
图片预览


文档简介
10.4 平移
一、选择题.
1.关于图形平移的特征叙述,有下列两种说法:①一个图形和它经过平移所得的图形中,两组对应点的连线一定平行;②一个图形和它经过平移所得的图形中,两组对应点的连线一定相等.其中判断正确的是( )
A.①错②对 B.①对②错 C.①②都错 D.①②都对
2.如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上),如果BC=8cm,EC=5cm,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
3.如图,甲、乙两只蚂蚁以相同的速度沿两条不同的路径,同时从点A出发爬到点B,下列判断正确的是( )
A.甲比乙先到 B.甲和乙同时到
C.乙比甲先到 D.无法确定
4.下列说法正确的是( )
A.平移前后图形大小可能改变
B.平移和旋转的共同之处是改变了图形的位置和大小
C.对应点到旋转中心的距离相等
D.由旋转得到的图形一定可以通过平移得到
5.如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
6.如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
二、填空题
7.如图是一块长方形的场地,长AB=72m,宽AD=31m,从A、B两处入口中的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为 m2.
8.如图,根据图中给出的数据判断两个图形的周长的关系: .(填“相等”或“不相等”或“无法判断”).
9.如图,△ABC中,BC=4cm.现将△ABC沿着垂直于BC的方向平移5cm,到△DEF的位置,则△ABC的边AC、AB所扫过的面积是 cm2.
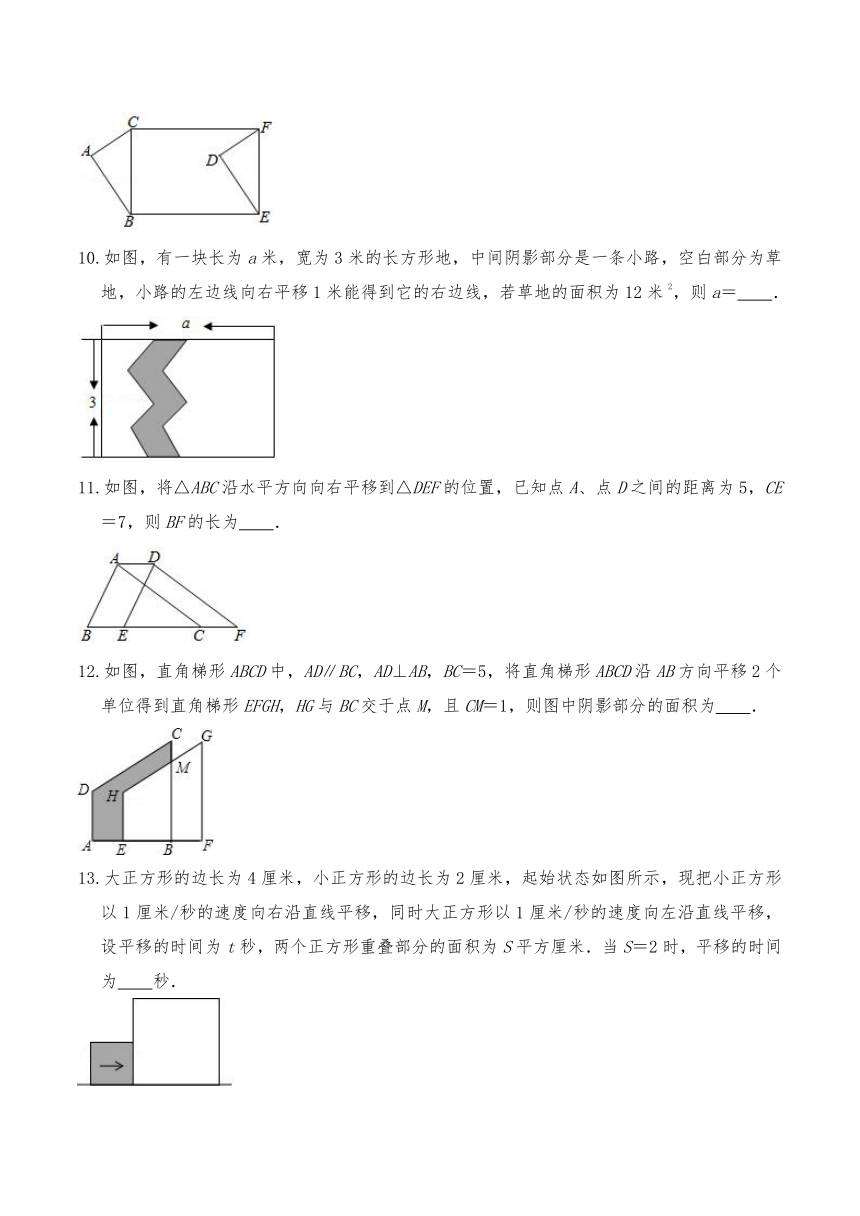
10.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a= .
11.如图,将△ABC沿水平方向向右平移到△DEF的位置,已知点A、点D之间的距离为5,CE=7,则BF的长为 .
12.如图,直角梯形ABCD中,AD∥BC,AD⊥AB,BC=5,将直角梯形ABCD沿AB方向平移2个单位得到直角梯形EFGH,HG与BC交于点M,且CM=1,则图中阴影部分的面积为 .
13.大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,现把小正方形以1厘米/秒的速度向右沿直线平移,同时大正方形以1厘米/秒的速度向左沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,平移的时间为 秒.
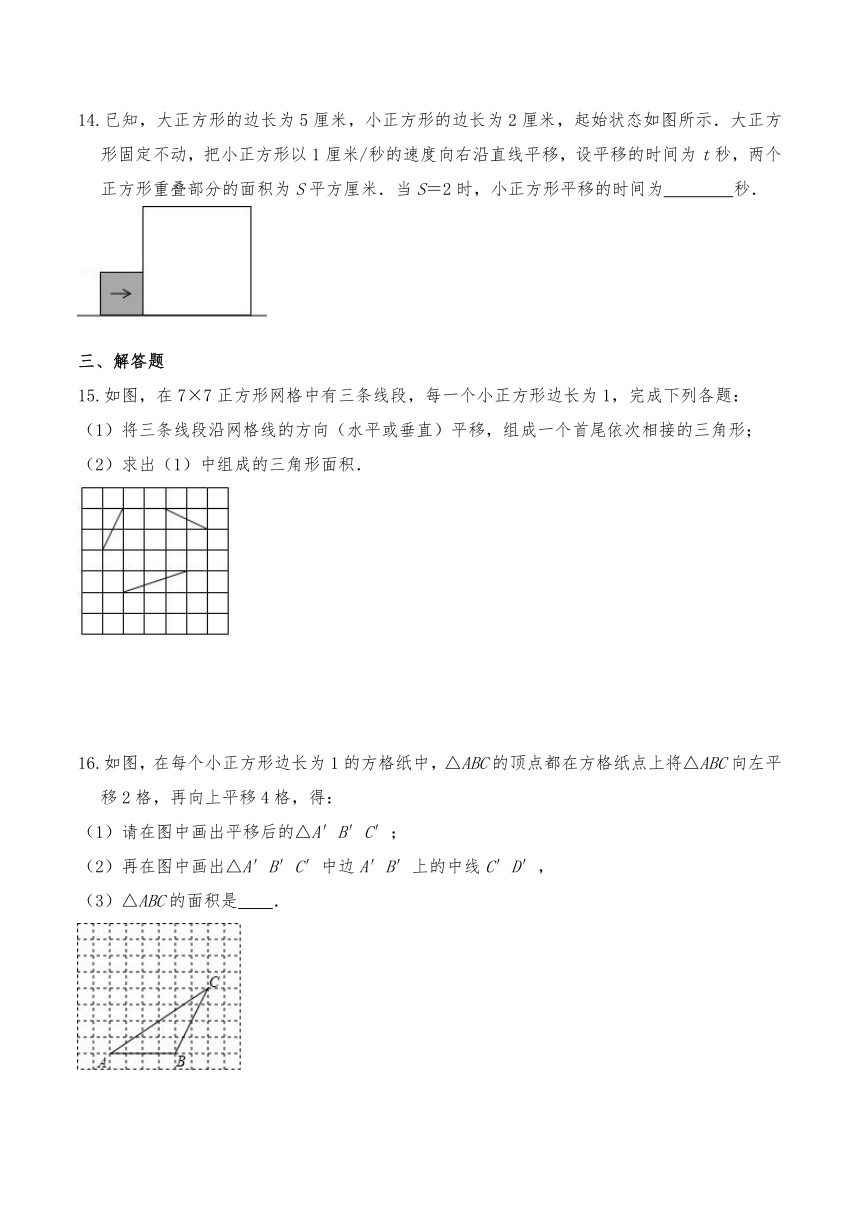
14.已知,大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为 秒.
三、解答题
15.如图,在7×7正方形网格中有三条线段,每一个小正方形边长为1,完成下列各题:
(1)将三条线段沿网格线的方向(水平或垂直)平移,组成一个首尾依次相接的三角形;
(2)求出(1)中组成的三角形面积.
16.如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸点上将△ABC向左平移2格,再向上平移4格,得:
(1)请在图中画出平移后的△A′B′C′;
(2)再在图中画出△A′B′C′中边A′B′上的中线C′D′,
(3)△ABC的面积是 .
17.如图所示,已知点A(2,1).B(8,2),C(6,3).
(1)若将△ABC向下平移5个单位长度,再向左平移9个单位长度,得到△A′B′C',画出平移后图形并写出各顶点的坐标.
(2)求△ABC的面积.
18.如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0),B(4,0),C(3,2).
(1)在所给的直角坐标系中画出三角形ABC;
(2)把三角形ABC向左平移3个单位,再向上平移2个单位得到三角形A′B′C′,画出三角形A′B′C′并写出点C′的坐标.
(3)求三角形A′B′C′的面积.
19.如图,已知射线CB∥DA,∠C=∠DAB=120°,E,F在射线CB上,且满足DB平分∠ADF,DE平分∠CDF.
(1)求证:CD∥BA;
(2)若左右平移AB,则∠DEC﹣∠DBF和∠DEC+∠DBA的值是否会改变,若不变,求出它们的值,若改变,请说明理由.
20.△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标:
A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
答案
一、选择题
A.A.B.C.D.A.
二、填空题
7.2100. 8.不相等. 9.20. 10.5. 11.17.
12.9. 13.0.5或2.5. 14.1或6.
三、解答题
15.解:(1)如图,△ABC为所作;
(2)S△ABC=3×2﹣×2×1﹣×2×1﹣×1×3=.
16.解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:中线C′D′即为所求;
(3)△ABC的面积是:×4×4=8.
故答案为:8.
17.解:(1)如图,△A′B′C'为所作;A′(﹣7,﹣4),B′(﹣1,﹣3),C′(﹣3,﹣2);
(2)S△ABC=6×2﹣×6×1﹣×2×1﹣×2×4=4.
18.解:(1)△ABC如图所示;
(2)△A′B′C′如图所示,A′(﹣4,2),B′(1,2),C′(0,4);
(3)由图可知,A′B′=1﹣(﹣4)=5,
点C′到A′B′的距离为2,
所以,△A′B′C′的面积=×5×2=5.
19.解:(1)∵CB∥DA,∠C=∠DAB=120°,
∴∠CDA=180°﹣∠C=180°﹣120°=60°,
∴∠CDA+∠DAB=180°,
∴CD∥BA;
(2)不变,理由如下:
∵CB∥DA,
∴∠DBF=∠ADB,
∵DB平分∠ADF,
∴∠FDB=∠ADB,
∴∠FDB=∠ADB=∠DBF,
∵DE平分∠CDF,
∴∠CDE=∠FDE,
∴∠EDB=∠FDE+∠FDB=∠CDA=×60°=30°;
∴∠DEC﹣∠DBF=∠EDB=30°;
∵∠DBA=∠ABC﹣∠EDB,
∴∠DEC+∠DBA=∠DEC+60°﹣∠DBF=30°+60°=90°.
∴∠DEC﹣∠DBF和∠DEC+∠DBA的值不变,分别是30°和90°.
20.解:(1)如图所示:
A′(﹣3,1),B′(﹣2,﹣2)、C′(﹣1,﹣1);
(2)A(1,3)变换到点A′的坐标是(﹣3,1),
横坐标减4,纵坐标减2,
∴点P的对应点P′的坐标是(a﹣4,b﹣2);
(3)△ABC的面积为:3×2﹣×2×2﹣×3×1﹣×1×1=2.
故答案为:(﹣3,1),(﹣2,﹣2)、(﹣1,﹣1);(a﹣4,b﹣2).
一、选择题.
1.关于图形平移的特征叙述,有下列两种说法:①一个图形和它经过平移所得的图形中,两组对应点的连线一定平行;②一个图形和它经过平移所得的图形中,两组对应点的连线一定相等.其中判断正确的是( )
A.①错②对 B.①对②错 C.①②都错 D.①②都对
2.如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上),如果BC=8cm,EC=5cm,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
3.如图,甲、乙两只蚂蚁以相同的速度沿两条不同的路径,同时从点A出发爬到点B,下列判断正确的是( )
A.甲比乙先到 B.甲和乙同时到
C.乙比甲先到 D.无法确定
4.下列说法正确的是( )
A.平移前后图形大小可能改变
B.平移和旋转的共同之处是改变了图形的位置和大小
C.对应点到旋转中心的距离相等
D.由旋转得到的图形一定可以通过平移得到
5.如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
6.如图,两个直角三角形重叠在一起,将△ABC沿AB方向平移2cm得到△DEF,CH=2cm,EF=4cm,下列结论:①BH∥EF;②AD=BE;③BD=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
二、填空题
7.如图是一块长方形的场地,长AB=72m,宽AD=31m,从A、B两处入口中的路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为 m2.
8.如图,根据图中给出的数据判断两个图形的周长的关系: .(填“相等”或“不相等”或“无法判断”).
9.如图,△ABC中,BC=4cm.现将△ABC沿着垂直于BC的方向平移5cm,到△DEF的位置,则△ABC的边AC、AB所扫过的面积是 cm2.
10.如图,有一块长为a米,宽为3米的长方形地,中间阴影部分是一条小路,空白部分为草地,小路的左边线向右平移1米能得到它的右边线,若草地的面积为12米2,则a= .
11.如图,将△ABC沿水平方向向右平移到△DEF的位置,已知点A、点D之间的距离为5,CE=7,则BF的长为 .
12.如图,直角梯形ABCD中,AD∥BC,AD⊥AB,BC=5,将直角梯形ABCD沿AB方向平移2个单位得到直角梯形EFGH,HG与BC交于点M,且CM=1,则图中阴影部分的面积为 .
13.大正方形的边长为4厘米,小正方形的边长为2厘米,起始状态如图所示,现把小正方形以1厘米/秒的速度向右沿直线平移,同时大正方形以1厘米/秒的速度向左沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,平移的时间为 秒.
14.已知,大正方形的边长为5厘米,小正方形的边长为2厘米,起始状态如图所示.大正方形固定不动,把小正方形以1厘米/秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.当S=2时,小正方形平移的时间为 秒.
三、解答题
15.如图,在7×7正方形网格中有三条线段,每一个小正方形边长为1,完成下列各题:
(1)将三条线段沿网格线的方向(水平或垂直)平移,组成一个首尾依次相接的三角形;
(2)求出(1)中组成的三角形面积.
16.如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸点上将△ABC向左平移2格,再向上平移4格,得:
(1)请在图中画出平移后的△A′B′C′;
(2)再在图中画出△A′B′C′中边A′B′上的中线C′D′,
(3)△ABC的面积是 .
17.如图所示,已知点A(2,1).B(8,2),C(6,3).
(1)若将△ABC向下平移5个单位长度,再向左平移9个单位长度,得到△A′B′C',画出平移后图形并写出各顶点的坐标.
(2)求△ABC的面积.
18.如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,在平面直角坐标系中,已知点A(﹣1,0),B(4,0),C(3,2).
(1)在所给的直角坐标系中画出三角形ABC;
(2)把三角形ABC向左平移3个单位,再向上平移2个单位得到三角形A′B′C′,画出三角形A′B′C′并写出点C′的坐标.
(3)求三角形A′B′C′的面积.
19.如图,已知射线CB∥DA,∠C=∠DAB=120°,E,F在射线CB上,且满足DB平分∠ADF,DE平分∠CDF.
(1)求证:CD∥BA;
(2)若左右平移AB,则∠DEC﹣∠DBF和∠DEC+∠DBA的值是否会改变,若不变,求出它们的值,若改变,请说明理由.
20.△ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标:
A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
答案
一、选择题
A.A.B.C.D.A.
二、填空题
7.2100. 8.不相等. 9.20. 10.5. 11.17.
12.9. 13.0.5或2.5. 14.1或6.
三、解答题
15.解:(1)如图,△ABC为所作;
(2)S△ABC=3×2﹣×2×1﹣×2×1﹣×1×3=.
16.解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:中线C′D′即为所求;
(3)△ABC的面积是:×4×4=8.
故答案为:8.
17.解:(1)如图,△A′B′C'为所作;A′(﹣7,﹣4),B′(﹣1,﹣3),C′(﹣3,﹣2);
(2)S△ABC=6×2﹣×6×1﹣×2×1﹣×2×4=4.
18.解:(1)△ABC如图所示;
(2)△A′B′C′如图所示,A′(﹣4,2),B′(1,2),C′(0,4);
(3)由图可知,A′B′=1﹣(﹣4)=5,
点C′到A′B′的距离为2,
所以,△A′B′C′的面积=×5×2=5.
19.解:(1)∵CB∥DA,∠C=∠DAB=120°,
∴∠CDA=180°﹣∠C=180°﹣120°=60°,
∴∠CDA+∠DAB=180°,
∴CD∥BA;
(2)不变,理由如下:
∵CB∥DA,
∴∠DBF=∠ADB,
∵DB平分∠ADF,
∴∠FDB=∠ADB,
∴∠FDB=∠ADB=∠DBF,
∵DE平分∠CDF,
∴∠CDE=∠FDE,
∴∠EDB=∠FDE+∠FDB=∠CDA=×60°=30°;
∴∠DEC﹣∠DBF=∠EDB=30°;
∵∠DBA=∠ABC﹣∠EDB,
∴∠DEC+∠DBA=∠DEC+60°﹣∠DBF=30°+60°=90°.
∴∠DEC﹣∠DBF和∠DEC+∠DBA的值不变,分别是30°和90°.
20.解:(1)如图所示:
A′(﹣3,1),B′(﹣2,﹣2)、C′(﹣1,﹣1);
(2)A(1,3)变换到点A′的坐标是(﹣3,1),
横坐标减4,纵坐标减2,
∴点P的对应点P′的坐标是(a﹣4,b﹣2);
(3)△ABC的面积为:3×2﹣×2×2﹣×3×1﹣×1×1=2.
故答案为:(﹣3,1),(﹣2,﹣2)、(﹣1,﹣1);(a﹣4,b﹣2).
