七年级数学下册试题 第10章《相交线、平行线与平移》单元测试卷 -沪科版(含答案)
文档属性
| 名称 | 七年级数学下册试题 第10章《相交线、平行线与平移》单元测试卷 -沪科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 201.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 22:38:11 | ||
图片预览




文档简介
第10章《相交线、平行线与平移》单元测试卷
一、选择题(本大题共12小题,每小题3分,共36分).
1.如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
2.如图,已知AB∥CD,∠BED=90°,则∠1与∠2之间的数量关系可表示为( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.无法表示
3.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
4.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
5.将直尺和一个含45°角的直角三角尺如图放置.若∠1=30°,则∠2的度数是( )
A.75° B.65° C.45° D.30°
6.如图,直线AB,CD相交于点O,下列条件:①∠AOD=90°;②∠AOC=∠BOC;③∠AOC=∠BOD,其中能说明AB⊥CD的有( )
A.0个 B.1个 C.2个 D.3个
7.如图,直线AB、CD相交于点O,∠DOF=90°,OF平分∠AOE,若∠BOD=32°,则∠DOE的度数为( )
A.32° B.48° C.58° D.64°
8.过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )
A. B.
C. D.
9.如图,平面内直线a∥b∥c,点A,B,C分别在直线a,b,c上,BD平分∠ABC,并且满足∠α>∠β,则∠α,∠β,∠γ关系正确的是( )
∠α=∠β+2∠γ B.∠α=∠β+∠γ
C.∠α=2∠β﹣2∠γ D.∠α=2∠β﹣∠γ
10.如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连结NE、NM,过点N作NG平分∠ENM交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF的度数为( )
A.110° B.115° C.120° D.125°
11.下列说法:
①相等的角是对顶角;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;
④同角或等角的余角相等,
其中正确的说法有( )
A.4 个 B.3 个 C.2 个 D.1 个
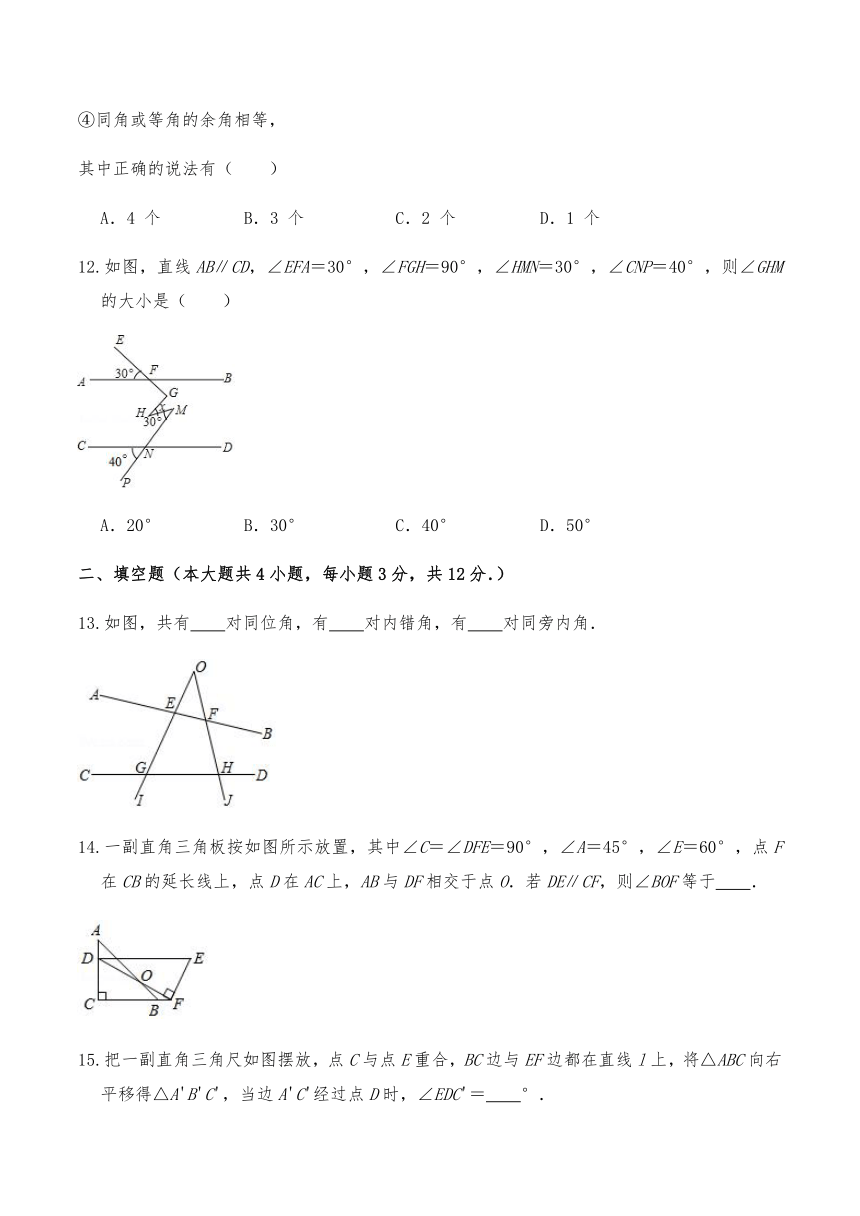
12.如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=40°,则∠GHM的大小是( )
A.20° B.30° C.40° D.50°
二、填空题(本大题共4小题,每小题3分,共12分.)
13.如图,共有 对同位角,有 对内错角,有 对同旁内角.
14.一副直角三角板按如图所示放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上,点D在AC上,AB与DF相交于点O.若DE∥CF,则∠BOF等于 .
15.把一副直角三角尺如图摆放,点C与点E重合,BC边与EF边都在直线l上,将△ABC向右平移得△A'B'C',当边A'C'经过点D时,∠EDC'= °.
16.某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ∥MN.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动 秒,两灯的光束互相平行.
三、解答题(本大题共7小题,共52分.)
17.如图,直线m∥n,△ABC的顶点B、C分别在直线n、m上,且∠ACB=90°,若∠1=50°.
求∠2的度数.
18.如图,直线AB、CD相交于点O,OM⊥AB,∠1=∠2.
(1)求∠NOD的度数;
(2)若∠AOD=3∠1,求∠AOC和∠MOD的度数.
19.如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
20.如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线的长短;
(2)小丽坐出租车由体育馆B到少年宫A,架设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果(2)中的这段路程长5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
21.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=70°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求直线a与b的距离.
22.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
23.如图1,已知三角形ABC与三角形ADE摆放在一起,点A、C、E在同一直线上,其中∠ACB=30°,∠DAE=45°,∠BAC=∠D=90°.如图2,固定三角形ABC,将三角形ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).
(1)当α为 度时,AD∥BC;
(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系;
(3)当三角形ADE的一边与三角形ABC的某一边平行(不共线)时,直接写出旋转角α所有可能的度数(第(1)题的结论除外).
答案
一、选择题
A.B.B.D.A.C.A.D.A.A.B.D.
二、填空题
13. 16;12;12.
14. 15°.
15.75.
16.30或110
三、解答题
17.解:∵m∥n
∴∠ECB=∠1=50°,
又∵∠ACB=∠BCE+∠ACE=90°,
∴∠ACE=40°,
又∵∠ACE+∠2=180°
∴∠2=140°.
18.证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴∠NOD=180°﹣∠CON=180°﹣90°=90°;
(2)∵∠AOD=3∠1,
∴∠NOD=2∠1=90°,
解得:∠1=45°,
∴∠AOC=∠AOM﹣∠1=90°﹣45°=45°;
∴∠BOD=90°﹣45°=45°,
∴∠MOD=∠BOD+∠BOM=45°+90°=135°.
故答案为:(1)90°; (2)45°,135°.
19.解:(1)OF⊥OD.
证明:∵OD平分∠BOE,OF平分∠AOE,
∴∠FOE=∠AOE,∠EOD=∠EOB.
∵∠AOE+∠EOB=180°,
∴∠FOD=∠FOE+∠EOD=(∠AOE+∠EOB)=90°.
∴OF⊥OD.
(2)∵∠AOC:∠AOD=1:5,∠AOC=∠BOD,
∴∠BOD:∠AOD=1:5.
∵∠AOD+∠BOD=180°,
∴∠BOD=30°,∠AOD=150°.
∵OD平分∠BOE,OF平分∠AOE,
∴∠BOE=2∠BOD=60°,∠EOF=∠AOE.
∵∠AOE+∠BOE=180°,
∴∠AOE=120°,
∴∠EOF=60°.
20.解:(1)如图所示:
根据平移可得:粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
(2)根据题意得:m=7+1.8(s﹣3)=(1.8s+1.6)(元);
(3)当s=5时,m=7+1.8×(5﹣3)=10.6>10,
∴小丽不能坐出租车由体育馆到少年宫.
21.解:(1)∵a∥b,
∴∠3=∠1=70°,
∵AC⊥AB,
∴∠2+∠3=90°,
∴∠2=90°﹣70°=20°.
答:∠2的度数为20°;
(2)∵AC=3,AB=4,BC=5,
设直线a与b的距离为h,
∴S△ABC=AC×AB=BC×h,
即5h=3×4,
∴h=.
答:直线a与b的距离为.
22.解:(1)如图1,过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°﹣160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)如图2,连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°﹣40°=120°.
23.解:(1)当α=15°时,AD∥BC,
图形如下:
故答案为15;
(2)设:∠CAD=γ,∠BAE=β,
①如上图,当α≤45°时,
α+β=90°,α+γ=45°,
故β﹣γ=45°;
②当45°<α≤90°时,
同理可得:γ+β=45°,
③当90°<α<180°时,
∠CAD+∠BAE=45°,
故:|∠CAD﹣∠BAE|=45°或∠CAD+∠BAE=45°;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的情况如下图所示:
①如图1,当DE∥AB时,α=45°;
②如图2,DE∥BC时,α=105°;
③如图3,当DE∥AC时,α=135°;
④如图4,当AE∥BC时,α=150°.
一、选择题(本大题共12小题,每小题3分,共36分).
1.如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A、D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
2.如图,已知AB∥CD,∠BED=90°,则∠1与∠2之间的数量关系可表示为( )
A.∠2=2∠1 B.∠2﹣∠1=90° C.∠1+∠2=180° D.无法表示
3.如图,直线b、c被直线a所截,则∠1与∠2是( )
A.内错角 B.同位角 C.同旁内角 D.对顶角
4.如图,直线AB、CD相交于点O,OE平分∠AOC,若∠BOD=70°,则∠COE的度数是( )
A.70° B.50° C.40° D.35°
5.将直尺和一个含45°角的直角三角尺如图放置.若∠1=30°,则∠2的度数是( )
A.75° B.65° C.45° D.30°
6.如图,直线AB,CD相交于点O,下列条件:①∠AOD=90°;②∠AOC=∠BOC;③∠AOC=∠BOD,其中能说明AB⊥CD的有( )
A.0个 B.1个 C.2个 D.3个
7.如图,直线AB、CD相交于点O,∠DOF=90°,OF平分∠AOE,若∠BOD=32°,则∠DOE的度数为( )
A.32° B.48° C.58° D.64°
8.过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )
A. B.
C. D.
9.如图,平面内直线a∥b∥c,点A,B,C分别在直线a,b,c上,BD平分∠ABC,并且满足∠α>∠β,则∠α,∠β,∠γ关系正确的是( )
∠α=∠β+2∠γ B.∠α=∠β+∠γ
C.∠α=2∠β﹣2∠γ D.∠α=2∠β﹣∠γ
10.如图,直线AB∥CD,点E、M分别为直线AB、CD上的点,点N为两平行线间的点,连结NE、NM,过点N作NG平分∠ENM交直线CD于点G,过点N作NF⊥NG,交直线CD于点F,若∠BEN=160°,则∠NGD﹣∠MNF的度数为( )
A.110° B.115° C.120° D.125°
11.下列说法:
①相等的角是对顶角;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;
④同角或等角的余角相等,
其中正确的说法有( )
A.4 个 B.3 个 C.2 个 D.1 个
12.如图,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=40°,则∠GHM的大小是( )
A.20° B.30° C.40° D.50°
二、填空题(本大题共4小题,每小题3分,共12分.)
13.如图,共有 对同位角,有 对内错角,有 对同旁内角.
14.一副直角三角板按如图所示放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上,点D在AC上,AB与DF相交于点O.若DE∥CF,则∠BOF等于 .
15.把一副直角三角尺如图摆放,点C与点E重合,BC边与EF边都在直线l上,将△ABC向右平移得△A'B'C',当边A'C'经过点D时,∠EDC'= °.
16.某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ∥MN.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动 秒,两灯的光束互相平行.
三、解答题(本大题共7小题,共52分.)
17.如图,直线m∥n,△ABC的顶点B、C分别在直线n、m上,且∠ACB=90°,若∠1=50°.
求∠2的度数.
18.如图,直线AB、CD相交于点O,OM⊥AB,∠1=∠2.
(1)求∠NOD的度数;
(2)若∠AOD=3∠1,求∠AOC和∠MOD的度数.
19.如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
20.如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.
(1)判断两条线的长短;
(2)小丽坐出租车由体育馆B到少年宫A,架设出租车的收费标准为:起步价为7元,3千米以后每千米1.8元,用代数式表示出租车的收费m元与行驶路程s(s>3)千米之间的关系;
(3)如果(2)中的这段路程长5千米,小丽身上有10元钱,够不够小丽坐出租车由体育馆到少年宫呢?说明理由.
21.如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=70°,求∠2的度数;
(2)若AC=3,AB=4,BC=5,求直线a与b的距离.
22.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
23.如图1,已知三角形ABC与三角形ADE摆放在一起,点A、C、E在同一直线上,其中∠ACB=30°,∠DAE=45°,∠BAC=∠D=90°.如图2,固定三角形ABC,将三角形ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).
(1)当α为 度时,AD∥BC;
(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系;
(3)当三角形ADE的一边与三角形ABC的某一边平行(不共线)时,直接写出旋转角α所有可能的度数(第(1)题的结论除外).
答案
一、选择题
A.B.B.D.A.C.A.D.A.A.B.D.
二、填空题
13. 16;12;12.
14. 15°.
15.75.
16.30或110
三、解答题
17.解:∵m∥n
∴∠ECB=∠1=50°,
又∵∠ACB=∠BCE+∠ACE=90°,
∴∠ACE=40°,
又∵∠ACE+∠2=180°
∴∠2=140°.
18.证明:(1)∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴∠NOD=180°﹣∠CON=180°﹣90°=90°;
(2)∵∠AOD=3∠1,
∴∠NOD=2∠1=90°,
解得:∠1=45°,
∴∠AOC=∠AOM﹣∠1=90°﹣45°=45°;
∴∠BOD=90°﹣45°=45°,
∴∠MOD=∠BOD+∠BOM=45°+90°=135°.
故答案为:(1)90°; (2)45°,135°.
19.解:(1)OF⊥OD.
证明:∵OD平分∠BOE,OF平分∠AOE,
∴∠FOE=∠AOE,∠EOD=∠EOB.
∵∠AOE+∠EOB=180°,
∴∠FOD=∠FOE+∠EOD=(∠AOE+∠EOB)=90°.
∴OF⊥OD.
(2)∵∠AOC:∠AOD=1:5,∠AOC=∠BOD,
∴∠BOD:∠AOD=1:5.
∵∠AOD+∠BOD=180°,
∴∠BOD=30°,∠AOD=150°.
∵OD平分∠BOE,OF平分∠AOE,
∴∠BOE=2∠BOD=60°,∠EOF=∠AOE.
∵∠AOE+∠BOE=180°,
∴∠AOE=120°,
∴∠EOF=60°.
20.解:(1)如图所示:
根据平移可得:粗线A→C→B和细线A→D→E→F→G→H→B的长相等;
(2)根据题意得:m=7+1.8(s﹣3)=(1.8s+1.6)(元);
(3)当s=5时,m=7+1.8×(5﹣3)=10.6>10,
∴小丽不能坐出租车由体育馆到少年宫.
21.解:(1)∵a∥b,
∴∠3=∠1=70°,
∵AC⊥AB,
∴∠2+∠3=90°,
∴∠2=90°﹣70°=20°.
答:∠2的度数为20°;
(2)∵AC=3,AB=4,BC=5,
设直线a与b的距离为h,
∴S△ABC=AC×AB=BC×h,
即5h=3×4,
∴h=.
答:直线a与b的距离为.
22.解:(1)如图1,过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°﹣160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)如图2,连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°﹣40°=120°.
23.解:(1)当α=15°时,AD∥BC,
图形如下:
故答案为15;
(2)设:∠CAD=γ,∠BAE=β,
①如上图,当α≤45°时,
α+β=90°,α+γ=45°,
故β﹣γ=45°;
②当45°<α≤90°时,
同理可得:γ+β=45°,
③当90°<α<180°时,
∠CAD+∠BAE=45°,
故:|∠CAD﹣∠BAE|=45°或∠CAD+∠BAE=45°;
(3)当△ADE的一边与△ABC的某一边平行(不共线)时,旋转角α的所有可能的情况如下图所示:
①如图1,当DE∥AB时,α=45°;
②如图2,DE∥BC时,α=105°;
③如图3,当DE∥AC时,α=135°;
④如图4,当AE∥BC时,α=150°.
