七年级数学下册试题 第10章《相交线、平行线与平移》单元卷 -沪科版(含答案)
文档属性
| 名称 | 七年级数学下册试题 第10章《相交线、平行线与平移》单元卷 -沪科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-16 00:00:00 | ||
图片预览


文档简介
第10章《相交线、平行线与平移》单元卷
一、选择题(本大题共12小题,每小题3分,共36分)
1.如图,∠1的同旁内角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.下列各项中,不是由平移设计的是( )
A. B. C. D.
3.如图,AB∥CD,BE平分∠ABC且过点D,∠CDE=160°,则∠C的度数是( )
A.110° B.120° C.130° D.140°
4.如图,在△ABC中已知∠B、∠C的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC点E,若AB=9,AC=7,则△ADE的周长为( )
A.13 B.14 C.15 D.16
5.如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10° B.20° C.30° D.40°
6.如图,已知△ABC中,AC+BC=36,AO,BO分别是角平分线,且∠3=∠5,分别交AC于N,BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
7.如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1) B.(1,3) C.(3,1) D.(3,﹣1)
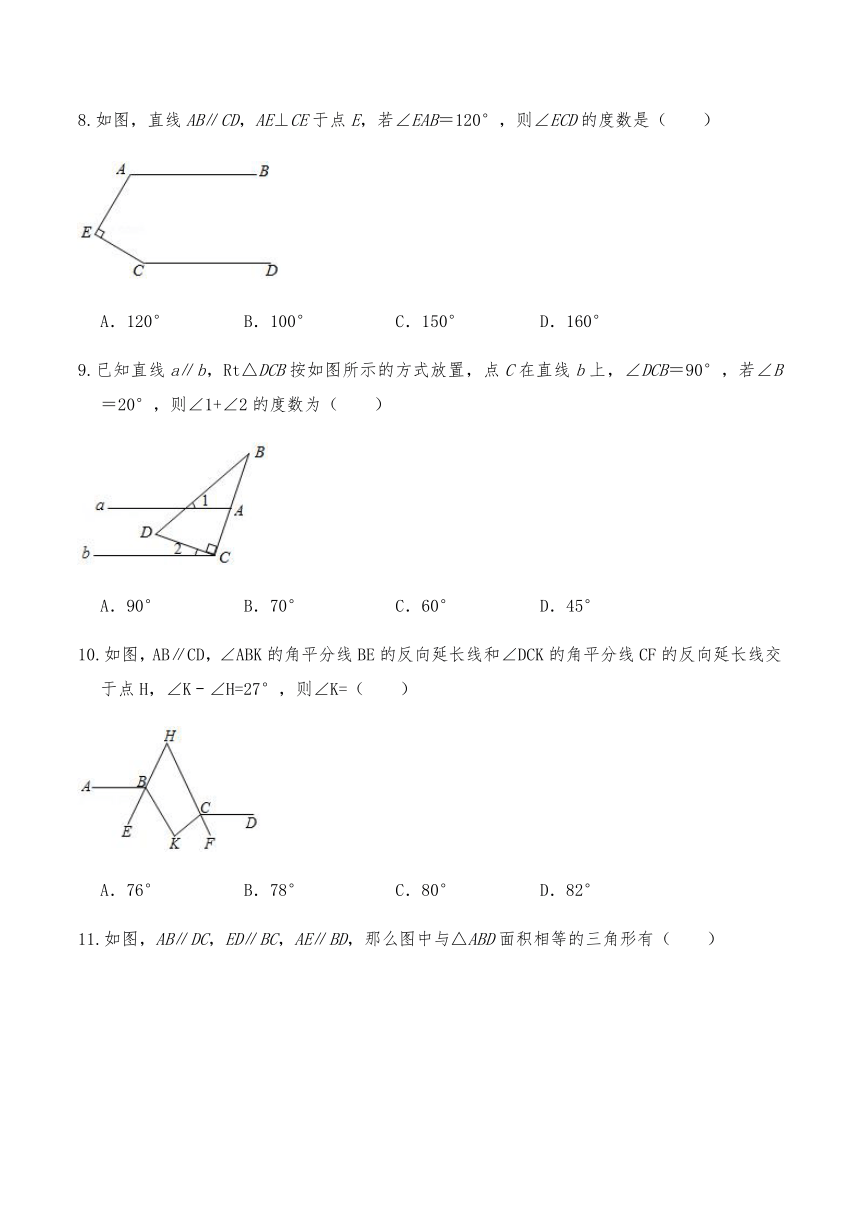
8.如图,直线AB∥CD,AE⊥CE于点E,若∠EAB=120°,则∠ECD的度数是( )
A.120° B.100° C.150° D.160°
9.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为( )
A.90° B.70° C.60° D.45°
10.如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
A.76° B.78° C.80° D.82°
11.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有( )
A.1个 B.2个 C.3个 D.4个
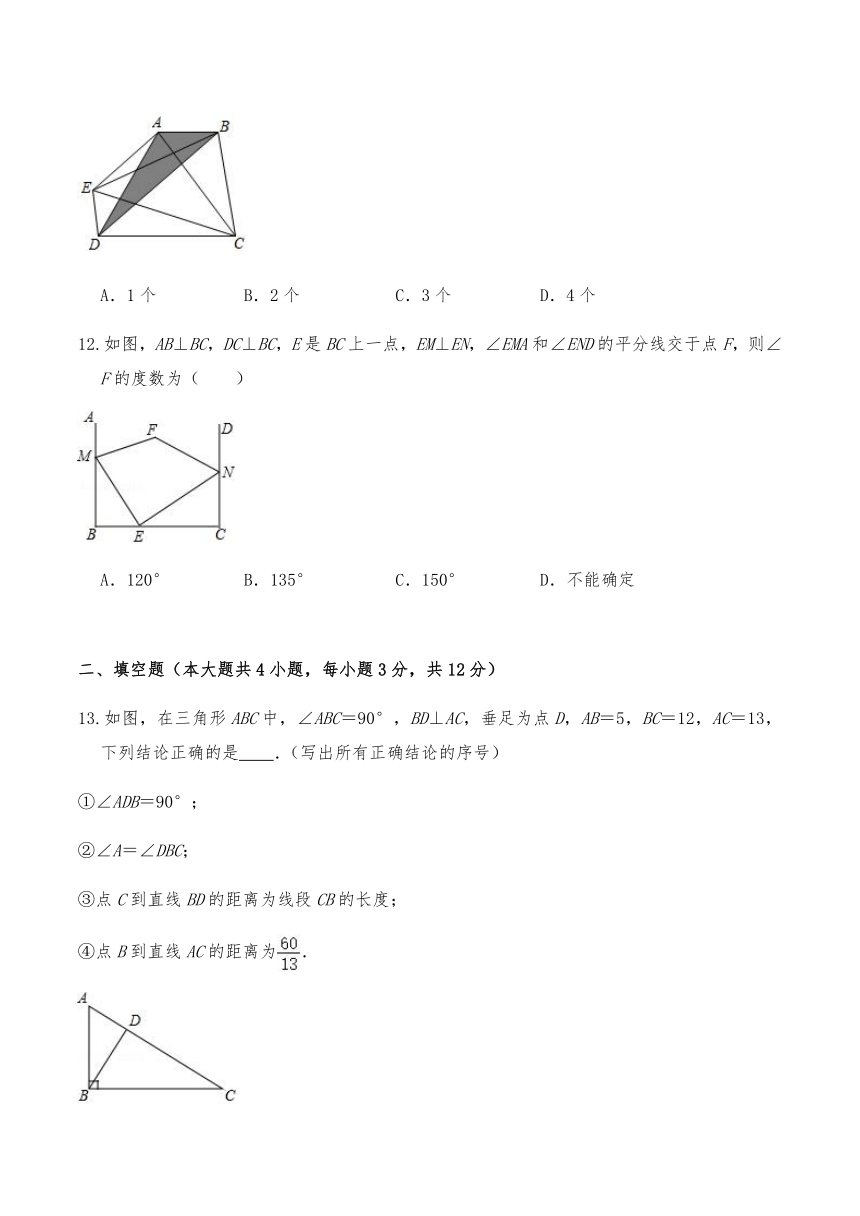
12.如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F的度数为( )
A.120° B.135° C.150° D.不能确定
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13,下列结论正确的是 .(写出所有正确结论的序号)
①∠ADB=90°;
②∠A=∠DBC;
③点C到直线BD的距离为线段CB的长度;
④点B到直线AC的距离为.
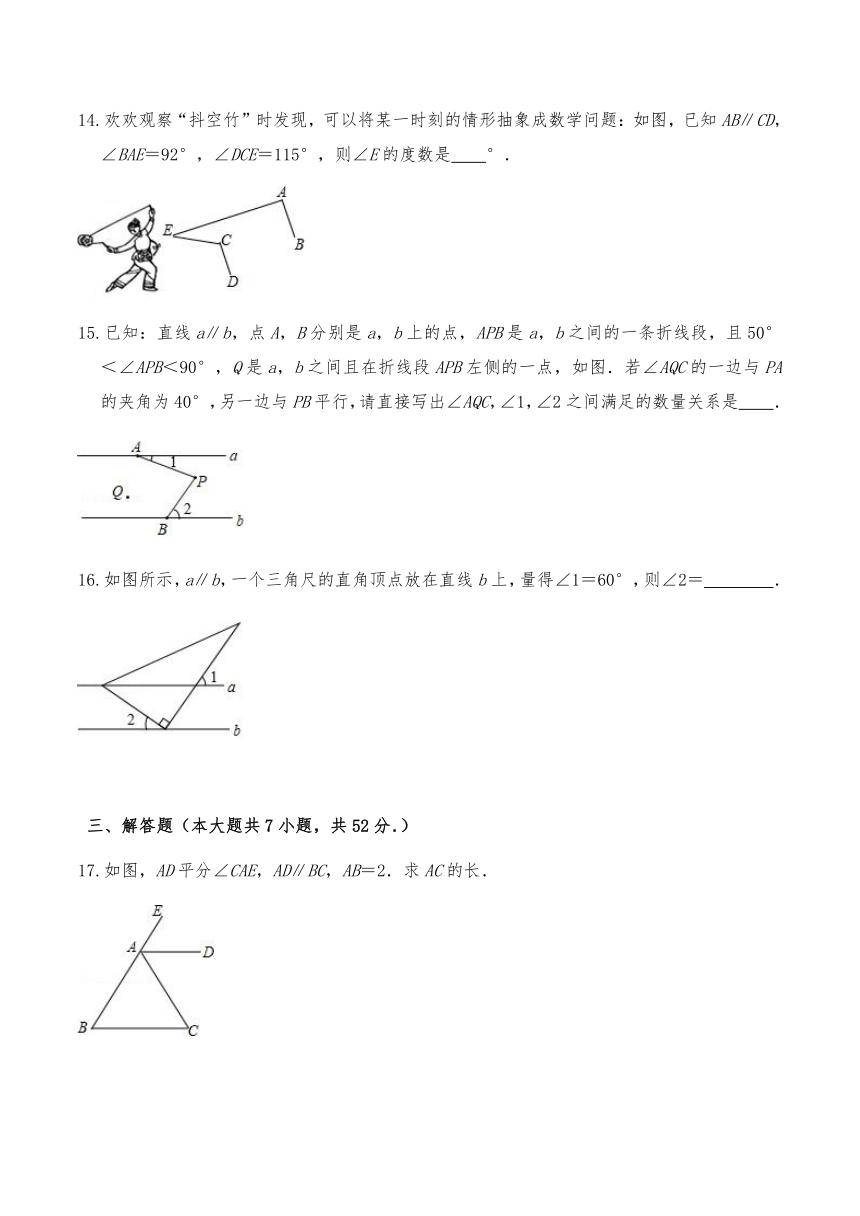
14.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是 °.
15.已知:直线a∥b,点A,B分别是a,b上的点,APB是a,b之间的一条折线段,且50°<∠APB<90°,Q是a,b之间且在折线段APB左侧的一点,如图.若∠AQC的一边与PA的夹角为40°,另一边与PB平行,请直接写出∠AQC,∠1,∠2之间满足的数量关系是 .
16.如图所示,a∥b,一个三角尺的直角顶点放在直线b上,量得∠1=60°,则∠2= .
三、解答题(本大题共7小题,共52分.)
17.如图,AD平分∠CAE,AD∥BC,AB=2.求AC的长.
18.如图,已知BE平分∠ABC,点D在射线BA上,且∠ABE=∠BED.
(1)判断BC与DE的位置关系,并说明理由.
(2)当∠ABE=25°时,求∠ADE的度数.
19.已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
20.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A'B'C'是△ABC平移之后得到的图象,并且C的对应点C'的坐标为(4,1).
(1)A'、B'两点的坐标分别为A' 、B' ;
(2)作出△ABC平移之后的图形△A'B'C';
(3)求△A'B'C'的面积.
21.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
22.(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.
23.【问题情境】:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,求∠APC的度数;
【问题迁移】:
如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
【问题应用】:
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
答案
一、选择题
D.D.D.D.B.C.D.C.B.B.C.B.
二、填空题
13.①②④.
14.23.
15.∠AQC+∠1+∠2=140°或∠AQC﹣∠1﹣∠2=40°.
16.30°
三、解答题
17.解:∵AD平分∠CAE,
∴∠EAD=∠DAC,
∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C,
∴∠B=∠C,
∴AB=AC=2.
18.解:(1)BC∥DE,理由如下:
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵∠ABE=∠BED,
∴∠EBC=∠BED,
∴BC∥DE;
(2)∵BE平分∠ABC,
∴∠ABC=2∠ABE=2×25°=50°,
∵BC∥DE,
∴∠ADE=∠ABC=50°.
19.解:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°(垂直的定义),
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠D=∠DBA(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠DBA,两直线平行,同位角相等;∠DBA,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
20.解:(1)A'、B'两点的坐标分别为A'(3,5)、B'(1,2);
故答案为(3,5)、(1,2);
(2)如图,△A'B'C'为所作;
(3)△A'B'C'的面积=3×4﹣×3×1﹣×4×1﹣×2×3=5.5.
21.证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB=∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
22.解:(1)∵CM平分∠ACD,AM平分∠BAC,
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°;
理由:如图2,过M作MF∥AB,
∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,
∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
23.(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
一、选择题(本大题共12小题,每小题3分,共36分)
1.如图,∠1的同旁内角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.下列各项中,不是由平移设计的是( )
A. B. C. D.
3.如图,AB∥CD,BE平分∠ABC且过点D,∠CDE=160°,则∠C的度数是( )
A.110° B.120° C.130° D.140°
4.如图,在△ABC中已知∠B、∠C的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC点E,若AB=9,AC=7,则△ADE的周长为( )
A.13 B.14 C.15 D.16
5.如图,E是直线CA上一点,∠FEA=40°,射线EB平分∠CEF,GE⊥EF.则∠GEB=( )
A.10° B.20° C.30° D.40°
6.如图,已知△ABC中,AC+BC=36,AO,BO分别是角平分线,且∠3=∠5,分别交AC于N,BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
7.如图,将一颗小星星放置在平面直角坐标系中第二象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向上平移2个单位长到丙位置,则小星星顶点A在丙位置中的对应点A'的坐标为( )
A.(﹣3,1) B.(1,3) C.(3,1) D.(3,﹣1)
8.如图,直线AB∥CD,AE⊥CE于点E,若∠EAB=120°,则∠ECD的度数是( )
A.120° B.100° C.150° D.160°
9.已知直线a∥b,Rt△DCB按如图所示的方式放置,点C在直线b上,∠DCB=90°,若∠B=20°,则∠1+∠2的度数为( )
A.90° B.70° C.60° D.45°
10.如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
A.76° B.78° C.80° D.82°
11.如图,AB∥DC,ED∥BC,AE∥BD,那么图中与△ABD面积相等的三角形有( )
A.1个 B.2个 C.3个 D.4个
12.如图,AB⊥BC,DC⊥BC,E是BC上一点,EM⊥EN,∠EMA和∠END的平分线交于点F,则∠F的度数为( )
A.120° B.135° C.150° D.不能确定
二、填空题(本大题共4小题,每小题3分,共12分)
13.如图,在三角形ABC中,∠ABC=90°,BD⊥AC,垂足为点D,AB=5,BC=12,AC=13,下列结论正确的是 .(写出所有正确结论的序号)
①∠ADB=90°;
②∠A=∠DBC;
③点C到直线BD的距离为线段CB的长度;
④点B到直线AC的距离为.
14.欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是 °.
15.已知:直线a∥b,点A,B分别是a,b上的点,APB是a,b之间的一条折线段,且50°<∠APB<90°,Q是a,b之间且在折线段APB左侧的一点,如图.若∠AQC的一边与PA的夹角为40°,另一边与PB平行,请直接写出∠AQC,∠1,∠2之间满足的数量关系是 .
16.如图所示,a∥b,一个三角尺的直角顶点放在直线b上,量得∠1=60°,则∠2= .
三、解答题(本大题共7小题,共52分.)
17.如图,AD平分∠CAE,AD∥BC,AB=2.求AC的长.
18.如图,已知BE平分∠ABC,点D在射线BA上,且∠ABE=∠BED.
(1)判断BC与DE的位置关系,并说明理由.
(2)当∠ABE=25°时,求∠ADE的度数.
19.已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
20.如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A'B'C'是△ABC平移之后得到的图象,并且C的对应点C'的坐标为(4,1).
(1)A'、B'两点的坐标分别为A' 、B' ;
(2)作出△ABC平移之后的图形△A'B'C';
(3)求△A'B'C'的面积.
21.如图:已知,∠HCO=∠EBC,∠BHC+∠BEF=180°.
(1)求证:EF∥BH;
(2)若BH平分∠EBO,EF⊥AO于F,∠HCO=64°,求∠CHO的度数.
22.(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.
23.【问题情境】:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,求∠APC的度数;
【问题迁移】:
如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
【问题应用】:
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
答案
一、选择题
D.D.D.D.B.C.D.C.B.B.C.B.
二、填空题
13.①②④.
14.23.
15.∠AQC+∠1+∠2=140°或∠AQC﹣∠1﹣∠2=40°.
16.30°
三、解答题
17.解:∵AD平分∠CAE,
∴∠EAD=∠DAC,
∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C,
∴∠B=∠C,
∴AB=AC=2.
18.解:(1)BC∥DE,理由如下:
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵∠ABE=∠BED,
∴∠EBC=∠BED,
∴BC∥DE;
(2)∵BE平分∠ABC,
∴∠ABC=2∠ABE=2×25°=50°,
∵BC∥DE,
∴∠ADE=∠ABC=50°.
19.解:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°(垂直的定义),
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠D=∠DBA(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠DBA,两直线平行,同位角相等;∠DBA,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
20.解:(1)A'、B'两点的坐标分别为A'(3,5)、B'(1,2);
故答案为(3,5)、(1,2);
(2)如图,△A'B'C'为所作;
(3)△A'B'C'的面积=3×4﹣×3×1﹣×4×1﹣×2×3=5.5.
21.证明:(1)∵∠HCO=∠EBC,
∴EB∥HC.
∴∠EBH=∠CHB.
∵∠BHC+∠BEF=180°,
∴∠EBH+∠BEF=180°.
∴EF∥BH.
(2)∵∠HCO=∠EBC,
∴∠HCO=∠EBC=64°,
∵BH平分∠EBO,
∴∠EBH=∠CHB=∠EBC=32°.
∵EF⊥AO于F,EF∥BH,
∴∠BHA=90°.
∴∠FHC=∠BHA+∠CHB=122°.
∵∠CHO=180°﹣∠FHC
=180°﹣122°
=58°.
22.解:(1)∵CM平分∠ACD,AM平分∠BAC,
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°;
理由:如图2,过M作MF∥AB,
∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,
∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
23.(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
