三角形的中位线[上学期]
图片预览

文档简介
三角形的中位线
教学目的:
1、 理解三角形中位线的概念,能说出它与三角形中线的区别。
2、 掌握三角形中位线定理,并能运用它进行简单的推理和计算。
3、 通过对问题的探索及进一步变式,培养学生逆向思维及分解构造基本图形解决比较复杂问题的能力。
教学重点:
三角形中位线的性质定理
教学难点:
证明三角形中位线性质定理时辅助线的添加和性质的灵活运用
教具:
多媒体课件
教学过程:
1、 复旧引新
1、 复习平行线等分线段定理及两个推论
2、 [边演示边提问]如图:若D是AB的中点,DE∥BC,交AC于E,则E是AC的中点;DF∥AC,交BC于F,则F是BC的中点。
2、 讲解新课
1、 三角形中位线的定义
连结EF[问]图中的DE、DF、EF是怎样的线段?它们的端点与三角形各边有什么关系?
DE、DF、EF是连结三角形两边中点的线段,我们称之为三角形的中位线。
除定义外,可把平行线等分线段定理的推论2看成三角形中位线的判定定理。
一个三角形有三条中位线。
2、 三角形中位线与三角形中线的区别
中线的一个端点是三角形一边的中点,另一端点是这边所对的顶点。中位线则是两边中点的连线。
3、 三角形中位线性质的猜想及证明
1 如图:DE是△ABC的一条中位线。
[让学生仔细观察,充分想象]猜想中位线可能具有什么特殊的性质。
猜想:DE∥BC,DE=BC
2 能证明这些猜想正确吗?
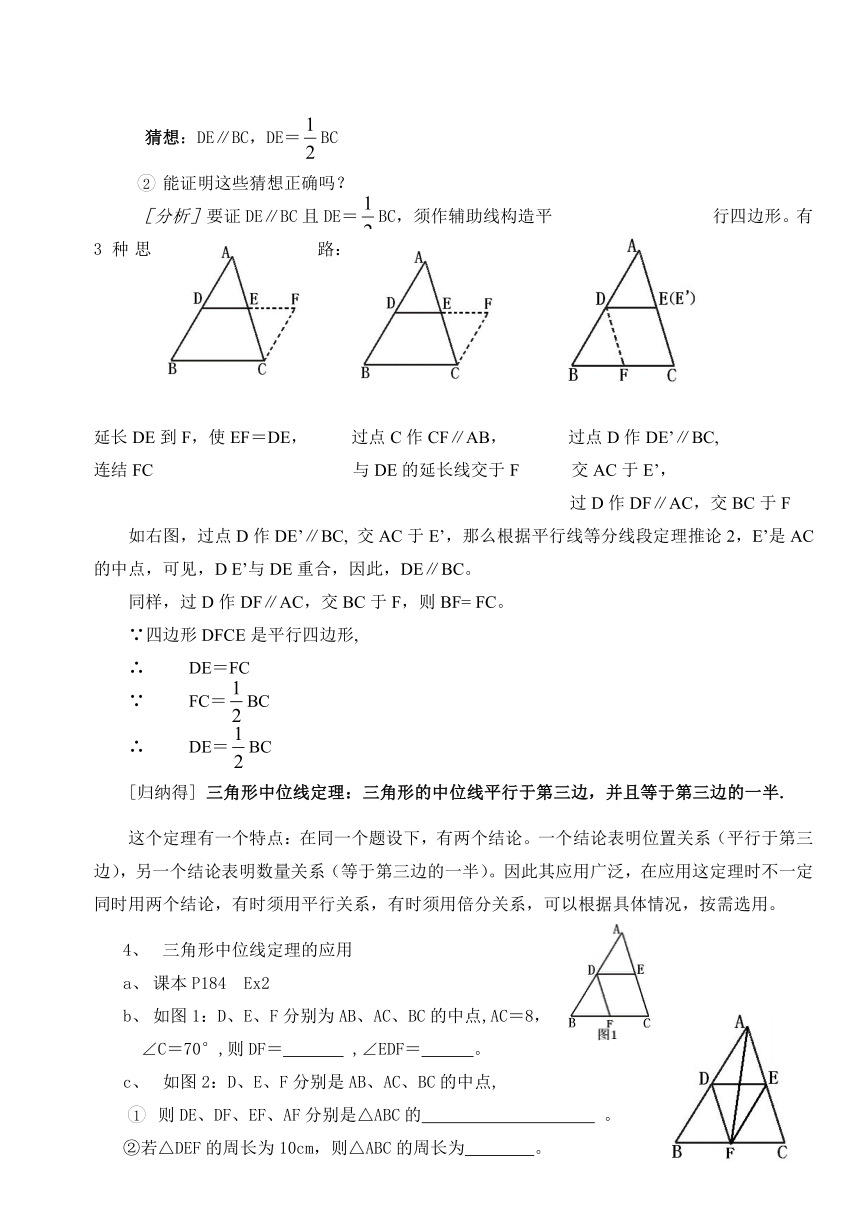
[分析]要证DE∥BC且DE=BC,须作辅助线构造平行四边形。有3种思路:
延长DE到F,使EF=DE, 过点C作CF∥AB, 过点D作DE’∥BC,
连结FC 与DE的延长线交于F 交AC于E’,
过D作DF∥AC,交BC于F
如右图,过点D作DE’∥BC, 交AC于E’,那么根据平行线等分线段定理推论2,E’是AC的中点,可见,D E’与DE重合,因此,DE∥BC。
同样,过D作DF∥AC,交BC于F,则BF= FC。
∵四边形DFCE是平行四边形,
∴ DE=FC
∵ FC=BC
∴ DE=BC
[归纳得] 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
这个定理有一个特点:在同一个题设下,有两个结论。一个结论表明位置关系(平行于第三边),另一个结论表明数量关系(等于第三边的一半)。因此其应用广泛,在应用这定理时不一定同时用两个结论,有时须用平行关系,有时须用倍分关系,可以根据具体情况,按需选用。
4、 三角形中位线定理的应用
a、 课本P184 Ex2
b、 如图1:D、E、F分别为AB、AC、BC的中点,AC=8,
∠C=70°,则DF= ,∠EDF= 。
c、 如图2:D、E、F分别是AB、AC、BC的中点,
1 则DE、DF、EF、AF分别是△ABC的 。
②若△DEF的周长为10cm,则△ABC的周长为 。
③若△ABC的面积为20cm2 ,则S△DEF= 。
[结论1]:三角形三条中位线围成的新三角形的周长等于原三角形周长的一半,面积等于原三角形面积的。
(口答)课本P184 Ex3
④AF、DE有何关系?
[结论2]:三角形的一条中位线与第三边上的中线互相平分。
5、 例1:求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。
分析:这是文字命题的证明题,要根据命题画出图形,写出已知,求证。
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
分析:这里已知点E、F、G、H分别是线段的中点,设法应用三角形中位线定理找到四边形EFGH的边之间的关系。如何构造三角形?(四边形的对角线把四边形分成两个三角形) 故连结AC
证明:连结AC
∵AH=HD,CG=GD,
∴HG∥AC,HG=AC(三角形中位线定理)
同理EF∥AC,EF=AC.
∴HG ∥ EF
所以四边形EFGH是平行四边形。
[问]:若连结EG、FH,这两条线段有什么关系?
结论:连结任意四边形对边中点的线段互相平分。
[引申]:
顺次连结任意四边形各边中点所得四边形是 ;顺次连结平行四边形各边中点所得四边形是 ;顺次连结矩形各边中点所得四边形是 ;顺次连结菱形各边中点所得四边形是 ;顺次连结正方形各边中点所得四边形是 ;顺次连结等腰梯形各边中点所得四边形是 。
归纳:
如果四边形的对角线相等,那么顺次连结各边中点所得的四边形是菱形。
如果四边形的对角线互相垂直,那么顺次连结各边中点所得的四边形是矩形。
如果四边形的对角线互相垂直且相等,那么顺次连结各边中点所得的四边形是正方形。
3、 巩固练习
a、 P184 Ex4
b、 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点,求证:BF = 4EF。
思路:遇到中点或三角形的中线时,常考虑是否可作中位线。因为中位线具有平移角和转化线段的功能。故“遇到中点想中位线”
4、 课堂小结
[师生共同小结]
1、本节课学习了什么内容?
2、应注意哪些概念之间和区别?(中线,中位线)
3、三角形中位线的判定方法有两种:定义、判定定理(平行线等分线段定理推论2)
4、三角形中位线定理是平行线等分线段定理推论2的逆定理,它提供了证明直线平行和线段数量关系的新方法,应用这个定理,关键在于找出(或构造)符合定理条件的基本图形。
运用中位线添辅助线的基本思路是:“遇到中点想中位线”。
讨论四边形有关问题时,常转化成三角形中的问题。
5、 布置作业
A组(必做)P188:4、6、7
B组(选做)如图,在等腰梯形ABCD中,MN分别是两底AB、CD的中点,E、F分别是DM、CM的中点,求证:EF和MN互相垂直平分
=
PAGE
教学目的:
1、 理解三角形中位线的概念,能说出它与三角形中线的区别。
2、 掌握三角形中位线定理,并能运用它进行简单的推理和计算。
3、 通过对问题的探索及进一步变式,培养学生逆向思维及分解构造基本图形解决比较复杂问题的能力。
教学重点:
三角形中位线的性质定理
教学难点:
证明三角形中位线性质定理时辅助线的添加和性质的灵活运用
教具:
多媒体课件
教学过程:
1、 复旧引新
1、 复习平行线等分线段定理及两个推论
2、 [边演示边提问]如图:若D是AB的中点,DE∥BC,交AC于E,则E是AC的中点;DF∥AC,交BC于F,则F是BC的中点。
2、 讲解新课
1、 三角形中位线的定义
连结EF[问]图中的DE、DF、EF是怎样的线段?它们的端点与三角形各边有什么关系?
DE、DF、EF是连结三角形两边中点的线段,我们称之为三角形的中位线。
除定义外,可把平行线等分线段定理的推论2看成三角形中位线的判定定理。
一个三角形有三条中位线。
2、 三角形中位线与三角形中线的区别
中线的一个端点是三角形一边的中点,另一端点是这边所对的顶点。中位线则是两边中点的连线。
3、 三角形中位线性质的猜想及证明
1 如图:DE是△ABC的一条中位线。
[让学生仔细观察,充分想象]猜想中位线可能具有什么特殊的性质。
猜想:DE∥BC,DE=BC
2 能证明这些猜想正确吗?
[分析]要证DE∥BC且DE=BC,须作辅助线构造平行四边形。有3种思路:
延长DE到F,使EF=DE, 过点C作CF∥AB, 过点D作DE’∥BC,
连结FC 与DE的延长线交于F 交AC于E’,
过D作DF∥AC,交BC于F
如右图,过点D作DE’∥BC, 交AC于E’,那么根据平行线等分线段定理推论2,E’是AC的中点,可见,D E’与DE重合,因此,DE∥BC。
同样,过D作DF∥AC,交BC于F,则BF= FC。
∵四边形DFCE是平行四边形,
∴ DE=FC
∵ FC=BC
∴ DE=BC
[归纳得] 三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
这个定理有一个特点:在同一个题设下,有两个结论。一个结论表明位置关系(平行于第三边),另一个结论表明数量关系(等于第三边的一半)。因此其应用广泛,在应用这定理时不一定同时用两个结论,有时须用平行关系,有时须用倍分关系,可以根据具体情况,按需选用。
4、 三角形中位线定理的应用
a、 课本P184 Ex2
b、 如图1:D、E、F分别为AB、AC、BC的中点,AC=8,
∠C=70°,则DF= ,∠EDF= 。
c、 如图2:D、E、F分别是AB、AC、BC的中点,
1 则DE、DF、EF、AF分别是△ABC的 。
②若△DEF的周长为10cm,则△ABC的周长为 。
③若△ABC的面积为20cm2 ,则S△DEF= 。
[结论1]:三角形三条中位线围成的新三角形的周长等于原三角形周长的一半,面积等于原三角形面积的。
(口答)课本P184 Ex3
④AF、DE有何关系?
[结论2]:三角形的一条中位线与第三边上的中线互相平分。
5、 例1:求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。
分析:这是文字命题的证明题,要根据命题画出图形,写出已知,求证。
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
分析:这里已知点E、F、G、H分别是线段的中点,设法应用三角形中位线定理找到四边形EFGH的边之间的关系。如何构造三角形?(四边形的对角线把四边形分成两个三角形) 故连结AC
证明:连结AC
∵AH=HD,CG=GD,
∴HG∥AC,HG=AC(三角形中位线定理)
同理EF∥AC,EF=AC.
∴HG ∥ EF
所以四边形EFGH是平行四边形。
[问]:若连结EG、FH,这两条线段有什么关系?
结论:连结任意四边形对边中点的线段互相平分。
[引申]:
顺次连结任意四边形各边中点所得四边形是 ;顺次连结平行四边形各边中点所得四边形是 ;顺次连结矩形各边中点所得四边形是 ;顺次连结菱形各边中点所得四边形是 ;顺次连结正方形各边中点所得四边形是 ;顺次连结等腰梯形各边中点所得四边形是 。
归纳:
如果四边形的对角线相等,那么顺次连结各边中点所得的四边形是菱形。
如果四边形的对角线互相垂直,那么顺次连结各边中点所得的四边形是矩形。
如果四边形的对角线互相垂直且相等,那么顺次连结各边中点所得的四边形是正方形。
3、 巩固练习
a、 P184 Ex4
b、 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点,求证:BF = 4EF。
思路:遇到中点或三角形的中线时,常考虑是否可作中位线。因为中位线具有平移角和转化线段的功能。故“遇到中点想中位线”
4、 课堂小结
[师生共同小结]
1、本节课学习了什么内容?
2、应注意哪些概念之间和区别?(中线,中位线)
3、三角形中位线的判定方法有两种:定义、判定定理(平行线等分线段定理推论2)
4、三角形中位线定理是平行线等分线段定理推论2的逆定理,它提供了证明直线平行和线段数量关系的新方法,应用这个定理,关键在于找出(或构造)符合定理条件的基本图形。
运用中位线添辅助线的基本思路是:“遇到中点想中位线”。
讨论四边形有关问题时,常转化成三角形中的问题。
5、 布置作业
A组(必做)P188:4、6、7
B组(选做)如图,在等腰梯形ABCD中,MN分别是两底AB、CD的中点,E、F分别是DM、CM的中点,求证:EF和MN互相垂直平分
=
PAGE
同课章节目录
