图形的变换[下学期]
图片预览
文档简介
第五单元 图形的认识
第29课 图形的轴对称
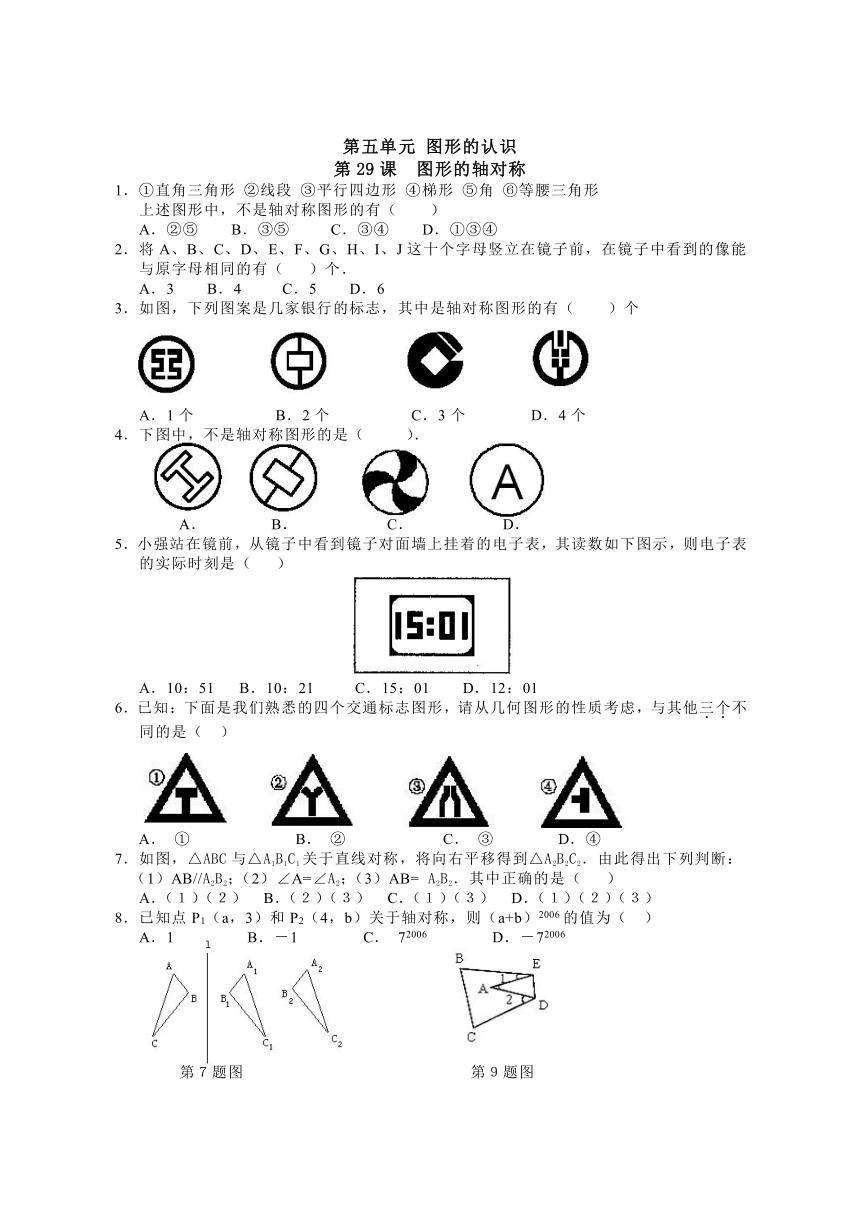
1.①直角三角形 ②线段 ③平行四边形 ④梯形 ⑤角 ⑥等腰三角形
上述图形中,不是轴对称图形的有( )
A.②⑤ B.③⑤ C.③④ D.①③④
2.将A、B、C、D、E、F、G、H、I、J这十个字母竖立在镜子前,在镜子中看到的像能与原字母相同的有( )个.
A.3 B.4 C.5 D.6
3.如图,下列图案是几家银行的标志,其中是轴对称图形的有( )个
A.1个 B.2个 C.3个 D.4个
4.下图中,不是轴对称图形的是( ).
A. B. C. D.
5.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如下图示,则电子表的实际时刻是( )
A.10:51 B.10:21 C.15:01 D.12:01
6.已知:下面是我们熟悉的四个交通标志图形,请从几何图形的性质考虑,与其他三个不同的是( )
A. ① B. ② C. ③ D.④
7.如图,△ABC与△A1B1C1关于直线对称,将向右平移得到△A2B2C2.由此得出下列判断:(1)AB//A2B2;(2)∠A=∠A2;(3)AB= A2B2.其中正确的是( )
A.(1)(2) B.(2)(3) C.(1)(3) D.(1)(2)(3)
8.已知点P1(a,3)和P2(4,b)关于轴对称,则(a+b)2006的值为( )
A.1 B.-1 C. 72006 D.-72006
第7题图 第9题图
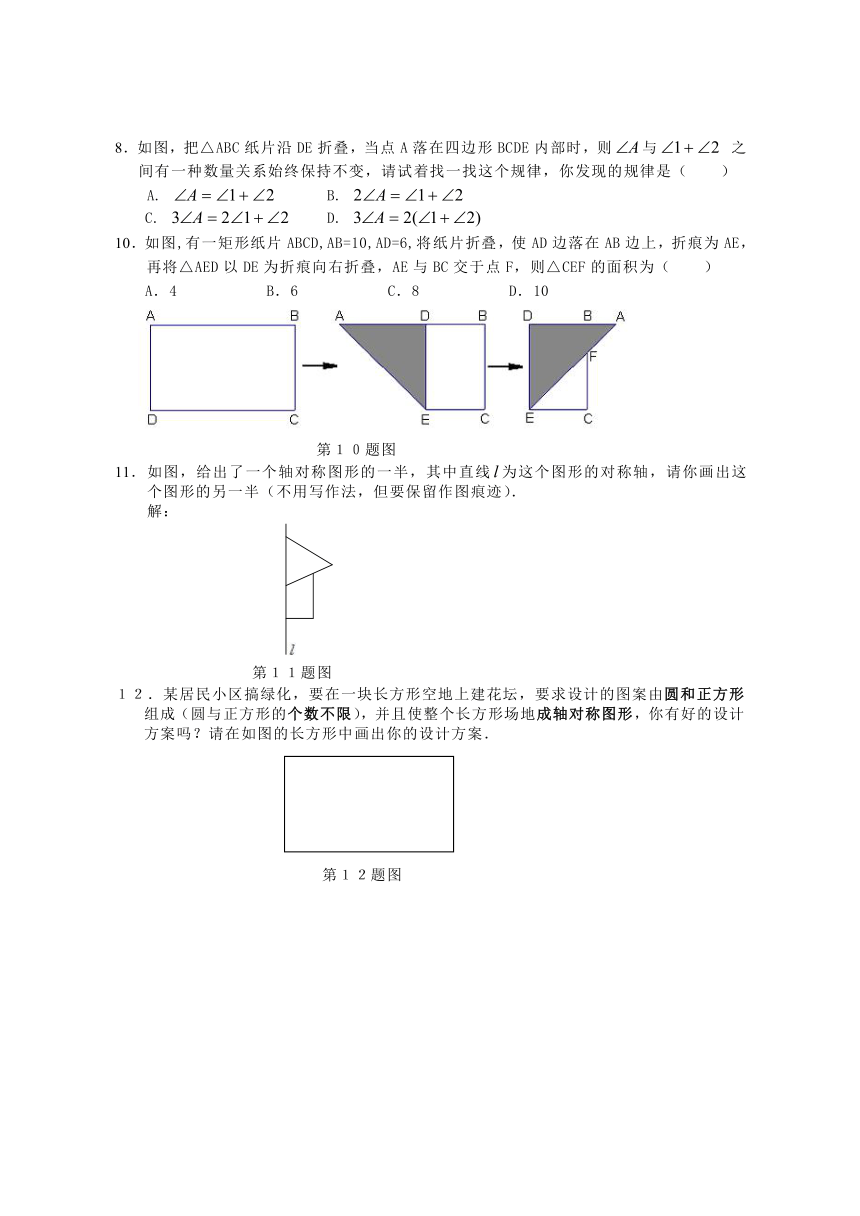
8.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则与 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A. B.
C. D.
10.如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
A.4 B.6 C.8 D.10
第10题图
11.如图,给出了一个轴对称图形的一半,其中直线为这个图形的对称轴,请你画出这个图形的另一半(不用写作法,但要保留作图痕迹).
解:
第11题图
12.某居民小区搞绿化,要在一块长方形空地上建花坛,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个长方形场地成轴对称图形,你有好的设计方案吗?请在如图的长方形中画出你的设计方案.
第12题图
第30课 图形的平移和旋转
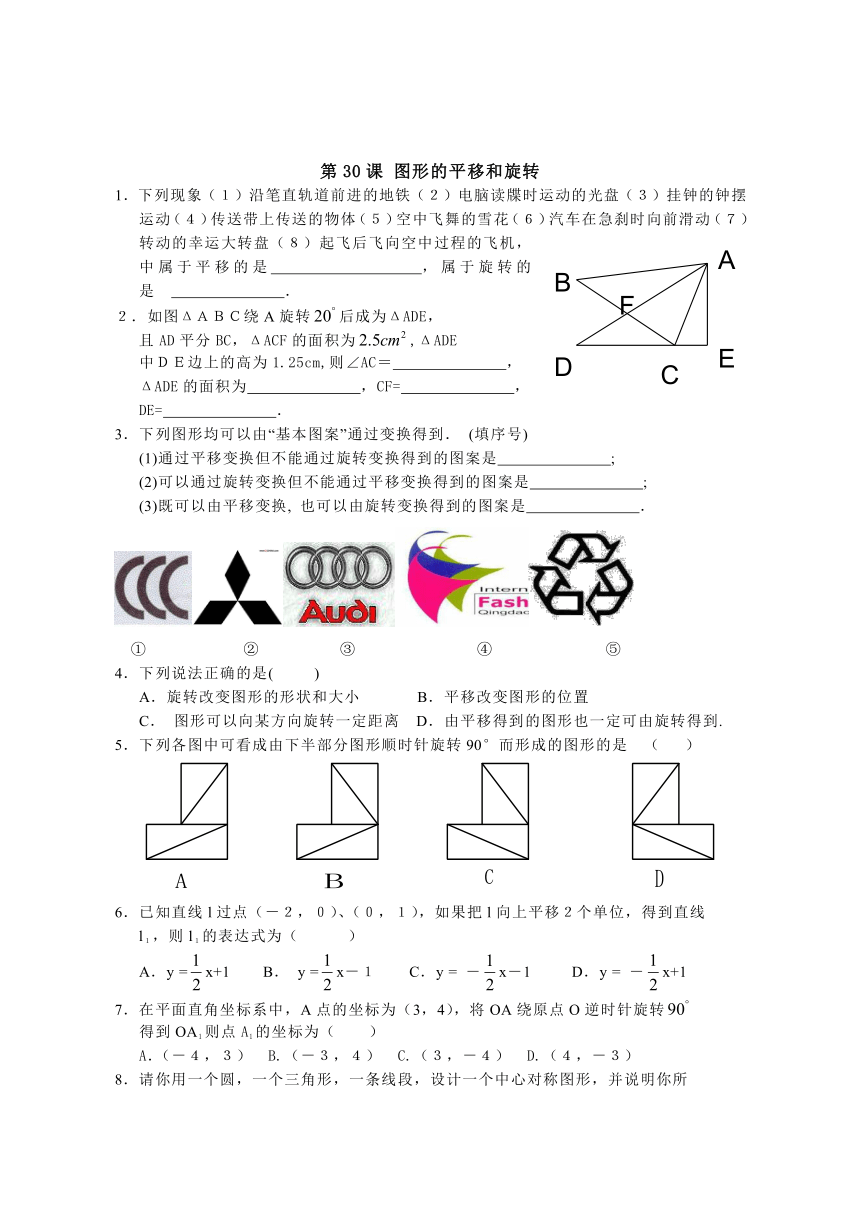
1.下列现象(1)沿笔直轨道前进的地铁(2)电脑读牒时运动的光盘(3)挂钟的钟摆运动(4)传送带上传送的物体(5)空中飞舞的雪花(6)汽车在急刹时向前滑动(7)转动的幸运大转盘(8)起飞后飞向空中过程的飞机,中属于平移的是 ,属于旋转的是 .
2.如图ΔABC绕A旋转后成为ΔADE,
且AD平分BC,ΔACF的面积为,ΔADE
中DE边上的高为1.25cm,则∠AC= ,
ΔADE的面积为 ,CF= ,
DE= .
3.下列图形均可以由“基本图案”通过变换得到. (填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是 ;
(2)可以通过旋转变换但不能通过平移变换得到的图案是 ;
(3)既可以由平移变换, 也可以由旋转变换得到的图案是 .
① ② ③ ④ ⑤
4.下列说法正确的是( )
A.旋转改变图形的形状和大小 B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离 D.由平移得到的图形也一定可由旋转得到.
5.下列各图中可看成由下半部分图形顺时针旋转90°而形成的图形的是 ( )
6.已知直线l过点(-2,0)、(0,1),如果把l向上平移2个单位,得到直线
l1,则l1的表达式为( )
A.y =x+1 B. y =x-1 C.y = ―x―1 D.y = ―x+1
7.在平面直角坐标系中,A点的坐标为(3,4),将OA绕原点O逆时针旋转
得到OA1则点A1的坐标为( )
A.(-4,3) B.(-3,4) C.(3,-4) D.(4,-3)
8.请你用一个圆,一个三角形,一条线段,设计一个中心对称图形,并说明你所
摆出的图案的含义.
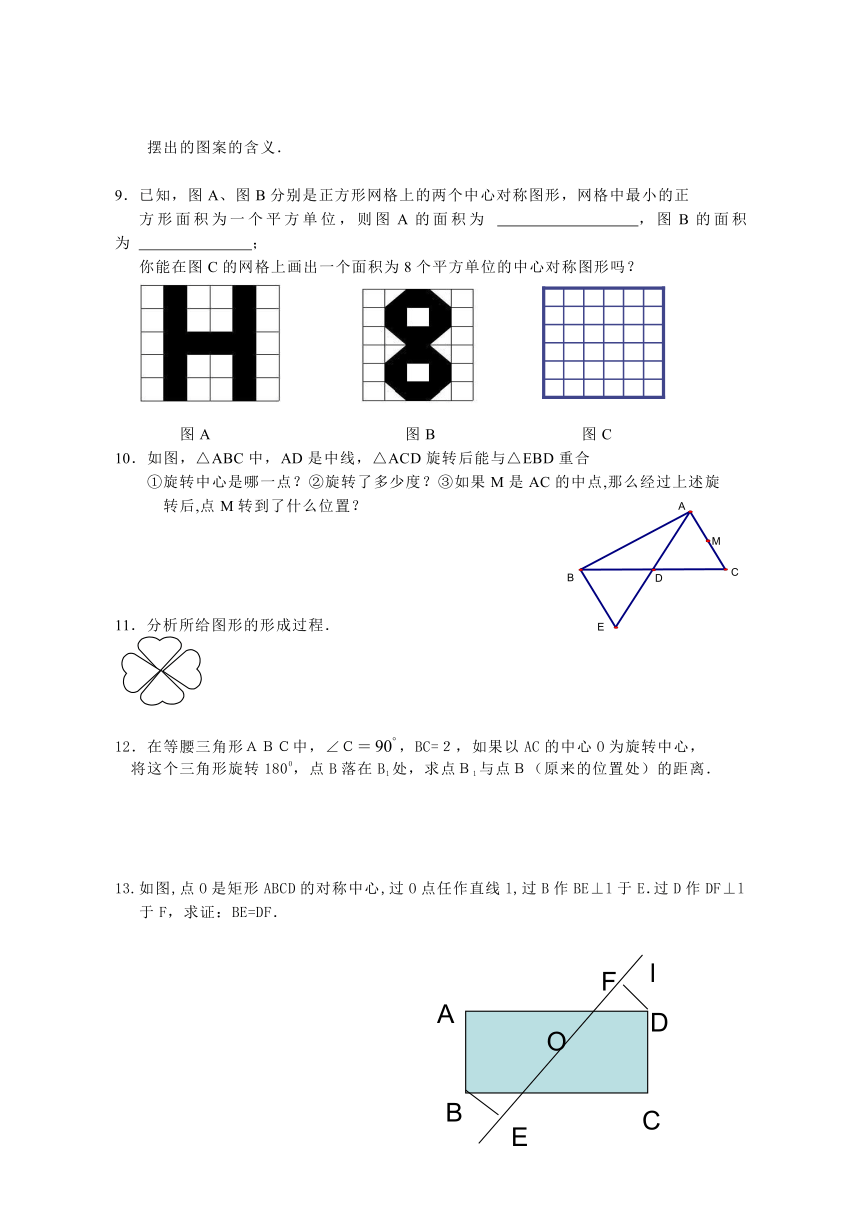
9.已知,图A、图B分别是正方形网格上的两个中心对称图形,网格中最小的正
方形面积为一个平方单位,则图A的面积为 ,图B的面积为 ;
你能在图C的网格上画出一个面积为8个平方单位的中心对称图形吗?
图A 图B 图C
10.如图,△ABC中,AD是中线,△ACD旋转后能与△EBD重合
①旋转中心是哪一点?②旋转了多少度?③如果M是AC的中点,那么经过上述旋
转后,点M转到了什么位置?
11.分析所给图形的形成过程.
12.在等腰三角形ABC中,∠C=,BC=2,如果以AC的中心O为旋转中心,
将这个三角形旋转1800,点B落在B1处,求点B1与点B(原来的位置处)的距离.
13.如图,点O是矩形ABCD的对称中心,过O点任作直线l,过B作BE⊥l于E.过D作DF⊥l
于F,求证:BE=DF.
第31课 图形的相似
1.如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则图中共有相似三角形( )
A.4对 B.5对 C.6对 D.7对
第1题图 第2题图 第3题图
2.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于D、E,若AD=4,BD=2,则DE:BC的值为( )
A.15 B.2 C. D.
3.如图,在平行四边形ABCD中,E为DC边的中点,AE交BD于点O,若=9,则等于( )
A.18 B.27 C.36 D.45
4.如图,△ABC中,AE⊥BC于E,D为AB边上一点,如果BD=2AD,CD=8,sin∠BCD=,那么AE的值为( )
A.3 B.6 C.7.2 D.9
第4题图 第5题图 第6题图
5.如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD;②△AOD∽△ACB;③: =DC:AB;④=,其中始终正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,要使△ACD∽△ABC,只需添加条件 (只要写出一个合适的条件即可).
7.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)6米的点A处,沿DA所在直线行走14米到点B时,人影长度变长 米
A D
B/
B M C
第7题图 第8题图 第9题图
8.矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点有 个.
9.如图,△ABC与△DEF是位似图形,相似比为2:3,已知AB=4,则DE的长等于 .
10.如图,AC⊥AB,BE⊥AB,AB=10,AC=2,用一块三角尺进行如下操作,将直角顶点P在线段AB上滑动,一直角边始终经过点C,另一直角边与BE相交于点D,若BD=8,则AP的长为 .
11.在方格纸中,每个小格的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在如图5×5的方格纸中,以A、B为顶点作格点三角形,与△ACB相似(相似比不能为1),则另一个顶点C的坐标为 米.
第10题图 第11题图 第12题图
12.如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积为S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第8个正方形的面积S8= .
13.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连结AE,图中有无相似三角形?若有,请写出,并对其中一对加以证明,若没有,请证明理由.
14.如图,PAB、PCD是⊙O的两条割线,AB是⊙O的直径,AC∥OD,
求证:(1)CD= (先填后证);
(2)若=,试求的
第32课 锐角三角函数(解直角三角形)
1.已知为锐角,且,则= .
2.在Rt△ABC中,∠C=90°,,AC=4,则BC= .
3.已知:如图,在△ABC中,∠A=30°,, ,则AB的长为 .
4.一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处(如图).上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里.(结果保留根号)
5.RtABC中,∠C=,∠A∶∠B=1∶2,则sinA的值( )
A. B. C. D.1
(第9题)
6.如图,在平面直角坐标系中,已知点A(3,0),点B(0,-4)则等
于( )
A. B. C. D.
7.·的值是( )
A.2-3 B. C.2- D.-1
8.在△ABC中∠C=900,a,b,c分别是∠A,∠B,∠C的对边,且,则的值( )
A. B. C. D.
9.在直角三角形中,各边的长度都扩大原来的m倍,则锐角A的各三角函数值( )
A.都扩大到m倍 B.都扩大到(m+1)倍 C.不变 D.不能确定
10.如图,两条宽度都是1的纸条,交叉重叠放在一起,则重叠部分的面积为( )
A. B. C. D.
11.沿坡角为30°的斜面前进100米,则上升的高度为( )
A. m B.m C.50 m D.50m
12.计算:
13.计算: 第10题图
14.如下图所示,在△ABC中,∠C=90°,D是AC边上一点,且,,求和.
15.某片绿地的形状如图,其中,ABBC,ADCD,AB=200米,CD=100米,求AD,BC的长.
16.某校的教室A位于工地O的正方向,且OA=200米,一部拖拉机从O点出发,以每秒5米的速度沿北偏西方向行驶,沿拖拉机的噪声污染半径为130米,试问教室A是否在拖拉机噪声污染范围内?若不在,请说明理由,若在,求出教室A受污染的时间有几秒?(已知 )
第33课 图形的变换与坐标的关系
1.在直角坐标系中,点P(-5,8)关于x轴对称点P1的坐标是 ;点P(-5,8)关于y轴对称点P2的坐标是 ;点P(-5,8)关于原点对称点P3 的坐标是 .
2.设点M(x , y)在第三象限,=2,=3,则点M关于原点对称的点N的坐标是
.
3.若点A(m,3)在函数y=5x+3的图像上,则点A关于原点对称的点B的坐标是 .
4.若点A关于y轴对称的点的坐标是(,-), 那么点A关于x轴对称的点C的坐标是 .
5.若点P关于原点对称的点P1的坐标是(,2),那么点P关于x轴对称的点P2的坐标是 .
6.若点P(m , n)其中m>0、n>0关于原点对称的点P1的坐标是 ,关于x轴对称的点P2的点的坐标是 ,关于y轴对称的点P3的坐标是 ,关于直线y=x对称的点P4的坐标是 ;关于直线y=-x对称的点P5的坐标是 ;
7.若点A(,3)与点B(,-3)关于原点对称, 则a= ,b= .
8.若直线y=-x+3的图像与抛物线y=x2 -3x-12的交点坐标是 ,它们关于y轴对称的点的坐标是 .
9.若直线y=3x+2的图像与直线y=-x+2的交点坐标是A,则点A关于y轴对称点B的坐标是 .
10.已知,点A(a+2 , b-4)与点A(-b,-3a)关于原点对称,则2006×2007= .
11.已知平面直角坐标系上的三个点O(0,0),A(-1,1),B(-1,0),将△ABO绕点O按顺时针方向旋转135,则点A、B的对应点A1、B1的坐标分别是A1( , ),B1( , ).
12.在△ABC中A(3,-1)、B(2,-1)、C(0,2) ,若将△ABC绕点C顺时针旋转90后得到△A1B1C1,则点A1的对应点的坐标是 .
13.已知,点P(x , y)的坐标满足+=0,则点P关于y轴对称的点P1在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.设M(x , y) 点在第三象限,且=3, =2,则M点关于y轴的对称点的坐标是( )
A.(3,2) B.(-3,-2) C.(-3,2) D.(3,-2)
15.点M(-,1)绕原点旋转60后的坐标是( )
A.(-,-1) B.(,1) C.(,-1) D.(-,-1)或(0,2)
16.如图1,在平面直角坐标系中, △ABC为等边三角形, 其中点A、B、C的坐标分别为(3,1)、(3,3),(3-,2),现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作的对称图形,得△A2B2C2
⑴直接写出A2 、B2两点的坐标;
⑵是否能通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请直接写出绕哪一点旋转多少度;你若认为不能, 请作出否定的回答(不必说明理由);
⑶设当△ABC的位置发生变化时,△A2B2C2、△A1B1C1与△ABC之间的对称关系始终保持不变:
①当△ABC向下平移多少个单位时,A1B1C1与A2B2C2完全重合?并直接写出此时C点的坐标;
②将△ABC绕点A顺时针针旋转α (0≤α≤180),使△A1B1C1与A2B2C2完全重合,此时α的值为多少?点C的坐标又是什么?
第五单元 图形的变换检测卷
(满分100分,时间60分钟)
一.填空题(每题3分,共36分)
1.如图,四边形ABCD是正方形,△ADE旋转后能与△ABF重合,则(1)旋转中心是 , 按 方向旋转了 度;(2)若连结EF,那么△AEF是 三角形.
2.如图,把两个大小完全相同的矩形拼成“L”形,则∠FAC= ,∠FCA= .
第1题图 第2题图 第3题图
3.如图,△ABC绕点C旋转到△,且与AC垂直,则∠= (填写角度)
4.如图,ABCD是一张矩形纸片,点O为矩形对角线的交点.直线MN经过点O交AD于M,交BC于N.先沿直线MN剪开,并将直角梯形MNCD绕点O旋转 度后,恰与直角梯形NMAB完全重合;再将重合后的直角梯形MNCD以直线MN为轴翻转后所得到的图形是下列中的 .(填写正确图形的代号)
5.已知,且,则.
6.如图,D、E、F分别是△ABC各边的中点,则△DEF与△ABC面积的比是 .
第4题图 第6题图 第7题图
7.如图,四边形ABCD与四边形EFGH相似,则∠H= .
8.要把一个三角形的面积扩大到原来面积的4倍,而它的形状不变,那么它的边长要扩大到原来的 倍.
9.如图,已知两座高度相等的建筑物AB、CD的水平距离BC=60米,在建筑物CD上有一铁塔PD,在塔顶P处观察建筑物的底部B和顶部A,分别测得俯角,建筑物AB的高等于 .(计算过程和结果一律不取近似值)
第9题图 第10题图 第11题图 第12题图
10.如图,AD∥EF∥BC,则图的相似三角形共有 对.
11.如图,正方形ABCD中,E是AD的中点,BM⊥CE,AB=6, 则BM= .
12.如图,ΔABC中,∠A=∠DBC, BC= ,SΔBCD∶SΔABC=2∶3, 则CD= .
二.选择题(每题4分,共36分)
13.下面四个图案中,既包含图形的旋转,又有图形的轴对称的设计是( )
A B C D
14.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
A. B. C. D.
15.如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且,则CE的长是( )
A. B. C. D.
第14题图 第15题图 第21题图
16.以下现象:(1)水管里水的流动(2)打针时针管的移动(3)射出的子弹(4)火车在笔直的铁轨上行驶,其中是平移的是( )
A.(1)(2) B.(1)(3) C.(2)(3) D.(2)(4)
17.在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是( ).
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
18.下列判断中,正确的是( ).
A.两个平行四边形一定相似 B.两个矩形一定相似
C.两个菱形一定相似 D.两个正方形一定相似
19.把一个矩形对折成两个相同的小矩形,如果这两个小矩形与原矩形相似,那么原矩形的长与宽的比值是( ).
A. B. C. D.
20.一个三角形的两边之比为a:b=3:1,则这两边上的高的比ha:hb为( )
A.3:1 B.1:3 C.9:1 D.1:9
21.如图,在平行四边形ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
A.4:5 B.3:5 C.4:9 D.3:8
三.解答题(22~24题,每题6分,25题10分)
22.在旷野上,一个人骑着马从A到B,半路上他必须在河边饮马一次,如图,他应该如何来选择饮马点P,才能使所走的
路程AP+PB最短呢?
23.如图网格中有一个四边形和两个三角形(各少一边).
(1)请你画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,
请写出这个整体图形对称轴的个数,这个整体图形至少
旋转多少度与自身重合?
24.如图,某船在A处测得灯塔B在北偏东30°方向,现该船从A处出发以每小时24海里的速度向正北方向航行15分钟到达C处,在C处测得灯塔B在北偏东45°的方向,求A到灯塔B的距离(结果取准确值)
25.如图,等腰梯形ABCD中,AD//BC,AD=3cm,BC=7cm, ∠B=60°,P为下底BC上一点,不与BC重合,连接AP,过P点作PE交DC于E,使得∠APE=∠B.
(1)求证:△ABP∽△PCE
(2)求等腰梯形的腰AB的长
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长,如果不存在,请说明理由.
空间与图形综合检测卷(一)
(总分100分,时间60分钟)
一.选择题(每题3分)
1.如图是由几个相同的小正方形搭成的集合体的
三种视图则搭成这个几何体的小正方形的
个数为( )
A.3 B.4 C.5 D.6 俯视图 主视图 左视图
2.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40,则∠DCF 等于( )
A.80 B.50 C.40 D.20
3.如图,B是线段AC的中点,过C点的直线l与AC成60的角.
在直线l上取一点,使得∠APB=30 则满足条件的点P 的个数是( )
A.3个 B.2个 C.1个 D.不存在
4.如图,在Rt△ABC中∠ACB=90 ,CD⊥AB于点D,已知AC=,BC = 2那么
Sin∠ACD= ( )
A. B. C. D.
5.如图, 小丽要制作一个圆锥模型,要求圆锥的母线长为10㎝那么小丽要制作的这个圆锥模型的侧面展开图的圆心角度数是( )
A.150 B.200 C.180 D.240
6.在矩形ABCD中,对角线AC、BD相交于点G、E为AD的中点,连接BE交AC于F, 连接FD.若∠BFA=90 则下列四对三角形(1)△BEA与△ACD ;(2)△FED与 △DEB;
(3)△CFD与△ABG; (4)△ADF 与△CFB.其中相似的为( )
A.(1)(4) B.(1)(2) C.(2)(3)(4) D.(1)(2)(3)
7.一个三角形的两边长为3和6第三边的边长为方程(x-2)(x-4)=0 的根,则这个三角形的周长是( )
A. 11 B. 11或13 C. 13 D. 11或13
8.将一个正方形纸片依次按图(1)图(2)方式对折然后沿着图(3)中的虚线裁剪.最后将图(4)的纸片再展开铺平.所得到图案是( )
图(1)(向上对折) 图(2)(向右对折)图(3)图(4)
A. B. C. D.
9.如图△ABC与△ABC关于直线l对称.将△ABC 向右平移得到△ABC由此得出下列判断:(1)AB=AB,(2)∠A=∠A,(3)AB=AB其中正确的是( )
A .(1) (2) B.(2) (3)
C .(1) (3) D.(1) (2) (3)
10.如图,一块含有30角的直角三角板ABC,在水平桌面
上绕点C按顺时针旋转到△ABC的位置若的BC长为15㎝,
那么顶点A从开始到结束所经过的路径长为( )
A.10∏㎝ B.10∏㎝ C.15㎝ D.20 ∏㎝
11.如图,在Rt△ABC中∠C=90,A C=4㎝,BC=6㎝ 动点P从点C沿C A,以1㎝/s的速度向点A运动.同时动点Q从点C沿CB,以2㎝/s的速度向点B运动,则运动过程中所构成的△CPQ的面积y(㎝)与运动时间x(s)之间的函数图像大致是( )
12.如图, ⊙O内切于△ABC,切点为D、E、F,若∠B=50,∠C=60 连结OE、OF、DE、DF,则∠EDF等于( )
A . 45 B . 55 C. 65 D .70
二.填空题(每题3分)
1.如图,PQ是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大
小等于 度.
第1题图 第3题图 第4题图
2.将点A(3,1)绕原点顺时针旋转90到点B.则B点的坐标是 .
3.如图是由9个等边三角形拼成的六边形, 若已知中间的小等边三角形的边长是a,则六边形的周长是 .
4.如图,在直角坐标系中,右边的图案是由左边的图案经过平移得到的, 左图案中左右眼睛的坐标分别是(-4,2),(-2,2)右图案中左眼的坐标是(3,4)则右图案中右眼的坐标是 .
5.如图,在△ABC中,AC= BC= 2,∠ACB=90,D是
边BC的中点,E是AB边上一动点, 则EC+ED的
最小值是 .
6.如图, 把矩形纸片OABC放入平面直角坐标系中,使 OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿着OB折叠,使点A落在点A的位置上.若OB=,tan∠BOC=,则点A的坐标为 .
三.解答题
1.如图, A、D、F、B在同一条直线上,AD=BF,AE=BC, 且AE∥BC.
求证:(1)△AEF≌△BCD;(2)EF∥CD.(8分)
2. 如图,图中的小方格都是边长为1的正方形,△ABC与△A1B1C1是关于点O为位似中心的为似图形,它们的顶点都在校正方形的顶点上.
(1) 画出位似中心点O;
(2) 求出△ABC与△A1B1C1的位似比;
(3) 以点O为位似中心,再画一个△A1B1C1,使得它与△ABC的位似比等于1.5.(9分)
3. 如图,某校九年级3班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚点A测得山腰上一点D的仰角为30,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45,山腰点D的俯角为60.请你帮助他们计算出小山的高度(计算过程和结果都不去近似值).(8分)
4. 如图, 在平行四边形ABCD中,∠DAB=60,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件的“∠DAB=60”,
上述的结论还成立吗?若成立,请
写出证明过程;若不成立,请说明理由.(9分)
5.在⊙O的内接△ABC中,AB+AC=12,AD⊥BC垂足为D,且AD=3,设⊙O的半径为y, AB的长为x.
(1)求y与x的函数关系式;
(2)当AB的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积.(9分)
6.如图,点T在⊙O上,延长⊙O的直径AB交TP于P,若PA=18,PT=12,PB=8.
(1)求证:△PTB∽△PAT;(2)求证:PT为⊙O的切线.
(3)在AT弧上是否存在一点C,使得BT=8TC?若存在,请证明;若不存在,请说明理由.(10分)
7.如图所示,在平面直角坐标系中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠COA=60,点P为x轴上的一个动点,点P不与点O、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当P运动什么位置时,使得∠CPD=∠OAB,且=,求这时P的坐标.(11分)
8.如图,已知P为∠AOB的边OA上的一点,以P为顶点的∠MPN的两边分别交射线OB于M、N两点,且∠MPN=∠AOB=α(α为锐角).当∠MPN以点P为旋转中心,PM边与PO重合的位置开始,按逆时针方向旋转(∠MPN保持不变)时,M、N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.若Sinα=、OP=2.
(1)当∠MPN旋转30(即∠OPM=30)时,求点N移动的距离;
(2)求证:△OPN∽△PMN;
(3)写出y与x之间的关系式;
(4)试写出S随x变化的函数关系式,并确定S的取值范围.
(12分)
第五单元 图形的认识
第29课 图形的轴对称答案
1.D 2.A 3.C 4.C 5.B 6.D 7.B 8.A 9.B 10.C
11.略 12.略
第30课 图形的平移与旋转答案
1.(1)(4)(6)(8);(2)(3)(7), 2. 80o;5cm2;4cm;8cm 3.①④;②⑤;③ 4. B 5. B 6. A 7. D 8. 略。 9.12,12,略 10.D点,180o,M为BE的中点。 11.略 12.连接BB1,则O在BB1上,在Rt BOC中,BC=2,OC=1,
所以OB=,所以B1B=2OB=2。 13.连接BD,因为矩形ABCD为中心对称图形,O为对称中心,所以O在BD上,且OB=OD,又因为∠BEO=∠DFO=90o,∠BPE=∠DOF,
所以ΔBEO≌ΔDFO,所以BE=DF。
第31课 图形的相似答案
1.B 2.C 3.C 4.D 5.C 6.∠ADC=∠ACB (∠ACD=∠ABC)
7.3.5米 8.2 9.6 10.2或8 11.(4,4)或(5,2) 12.128
13.有 △ADE∽△AEC,证明略 14.(1)CD=BD 证明略 (2) ,
第32课 锐角三角函数(含解直角三角形)答案
1. 2. 3. 4.5.A 6.C 7.A 8.B 9.C 10.C 11.C 12.解:原式=1 13.解:原式=1
14.解:在Rt△CDB中,,,∴.
在Rt△ABC中,,,∴.
15.解:Rt△ABC中
∠E=900-∠A=900-600=300
RT△CDE中
16.解:由题意可知,OA=200米 作AB⊥OM于B,
教室A在噪音范围内
由题意知,在OM上取两点C、D,得AC=AD=130米
AB⊥OM 米
米 米
受污染时间为秒
第33课 图形的变换与坐标的关系答案
1.(-5,-8),(5,8),(5,-8)。 2.(2, 8)、(2, 2)。 3.(0,-3)。
4.(-,)。 5.(-,2 )。 6.(-m,-n),(m,-n),(-m,n),(n,m),(-n,-m)。 7. 2 ,2。 8.(-3,6)、(5,-2),(-5,-2)、(3,6)。
9.(0,2)。 10. 2007。 11. 0 。 12.(-1,-3) 13.C 14. D 15. D 16.(1)(3,-1),(-3,-3) (2) 能 绕点O旋转180 ① 2 (3-,0) 180 (3+,0)。
第五单元 图形与变换检测卷答案
一.填空题
1.A 顺时针 90度 等腰直角三角形 2.90度,45度 3.55度
4.180度,D 5.x=6,y=10 6.1:4 7.67度 8.2 9.60-20
10.3 11. 12.
二.选择题:
13.D 14.B 15.D 16.D 17.C 18.D 19.C 20.B
21.C
空间与图形综合检测卷(1)答案
一.选择题:1.B 2.D 3.B 4.A 5.B 6.D 7.C 8.D 9.B 10.D 11.C 12.B
二.填空题:1. 120 2. (1,-3) 3. 30 a 4. (5,4) 5. 6. (-,)
三.解答题
1.略 2. (1).略 (2). 位似比为 1:2 (3). 略 3. 90(+1)米 4. (1) 略 (2)还成立.证明略
5. (1).y=-x2+2x. (2).当x=6时y取最大值6.⊙O的最大面积为36π.
6.(1)证明:在△PBT和△PTA中,∵∠BPT=∠TPA,∵==,= = ,
∴ = ∴△PBT∽△PTA (2).连结OT,.∵OB=OT∴∠OBT=∠BTO.由(1)得∠PTB=∠PAT.∵AB是直径,∴∠BTA=900,∴∠A+∠ABT=900,∴∠OTB+∠BTP=900,∴PT是⊙O的切线. (3)解:∵∠ABT=∠P+∠PTB,∴∠ABT>∠P.过B作BC交⊙O于C,使∠BCT=∠P. 由(1)得∠PTB=∠PAT= ∠BCT∴△PBT∽△BTC∴= , 又PB=8, ∴BT2=8TC 存在一点 C 使得BT2=8TC.
7. (1);过C作CD⊥OA于A,BE⊥OA于E 则△OCD≌△ABE,四边形CDEB为矩形
∴OD=AE,CD=BE∵OC=AB=4,∠COA=60°∴CD=,OD=2 ∴CB=DE=3
∴OE=OD+DE=5 ∵BE=CD=∴B(5,)
(2)∵∠COA=60°,△OCP为等腰三角形∴△OCP是等边三角形
∴OP=OC=4 ∴P(4,0)即P运动到(4,0)时,△OCP为等腰三角形
(3)∵∠CPD=∠OAB=∠COP=60°∴∠OPC+∠DPA=120°又∵∠PDA+∠DPA=120°
∴∠OPC=∠PDA∵∠OCP=∠A=60°∴△COP∽△PAD ∴
∵,AB=4 ∴BD= ∴AD= 即 ∴
得OP=1或6∴P点坐标为(1,0)或(6,0)
8.解 : (1)点N移动的距离为2. (2).略 (3) y= (4)0≤S<
B
A
C
D
E
F
O
A
B
C
D
E
F
l
A
B
x
y
O
A(3,0)
0
x
y
B(0,-4)
A
B
C
D
图图1 图2
第3题图
第4题图
第5题图
第6题图
A
B
C
D
E
北
东
O
A
M
B
C
D
第29课 图形的轴对称
1.①直角三角形 ②线段 ③平行四边形 ④梯形 ⑤角 ⑥等腰三角形
上述图形中,不是轴对称图形的有( )
A.②⑤ B.③⑤ C.③④ D.①③④
2.将A、B、C、D、E、F、G、H、I、J这十个字母竖立在镜子前,在镜子中看到的像能与原字母相同的有( )个.
A.3 B.4 C.5 D.6
3.如图,下列图案是几家银行的标志,其中是轴对称图形的有( )个
A.1个 B.2个 C.3个 D.4个
4.下图中,不是轴对称图形的是( ).
A. B. C. D.
5.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如下图示,则电子表的实际时刻是( )
A.10:51 B.10:21 C.15:01 D.12:01
6.已知:下面是我们熟悉的四个交通标志图形,请从几何图形的性质考虑,与其他三个不同的是( )
A. ① B. ② C. ③ D.④
7.如图,△ABC与△A1B1C1关于直线对称,将向右平移得到△A2B2C2.由此得出下列判断:(1)AB//A2B2;(2)∠A=∠A2;(3)AB= A2B2.其中正确的是( )
A.(1)(2) B.(2)(3) C.(1)(3) D.(1)(2)(3)
8.已知点P1(a,3)和P2(4,b)关于轴对称,则(a+b)2006的值为( )
A.1 B.-1 C. 72006 D.-72006
第7题图 第9题图
8.如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则与 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A. B.
C. D.
10.如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积为( )
A.4 B.6 C.8 D.10
第10题图
11.如图,给出了一个轴对称图形的一半,其中直线为这个图形的对称轴,请你画出这个图形的另一半(不用写作法,但要保留作图痕迹).
解:
第11题图
12.某居民小区搞绿化,要在一块长方形空地上建花坛,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个长方形场地成轴对称图形,你有好的设计方案吗?请在如图的长方形中画出你的设计方案.
第12题图
第30课 图形的平移和旋转
1.下列现象(1)沿笔直轨道前进的地铁(2)电脑读牒时运动的光盘(3)挂钟的钟摆运动(4)传送带上传送的物体(5)空中飞舞的雪花(6)汽车在急刹时向前滑动(7)转动的幸运大转盘(8)起飞后飞向空中过程的飞机,中属于平移的是 ,属于旋转的是 .
2.如图ΔABC绕A旋转后成为ΔADE,
且AD平分BC,ΔACF的面积为,ΔADE
中DE边上的高为1.25cm,则∠AC= ,
ΔADE的面积为 ,CF= ,
DE= .
3.下列图形均可以由“基本图案”通过变换得到. (填序号)
(1)通过平移变换但不能通过旋转变换得到的图案是 ;
(2)可以通过旋转变换但不能通过平移变换得到的图案是 ;
(3)既可以由平移变换, 也可以由旋转变换得到的图案是 .
① ② ③ ④ ⑤
4.下列说法正确的是( )
A.旋转改变图形的形状和大小 B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离 D.由平移得到的图形也一定可由旋转得到.
5.下列各图中可看成由下半部分图形顺时针旋转90°而形成的图形的是 ( )
6.已知直线l过点(-2,0)、(0,1),如果把l向上平移2个单位,得到直线
l1,则l1的表达式为( )
A.y =x+1 B. y =x-1 C.y = ―x―1 D.y = ―x+1
7.在平面直角坐标系中,A点的坐标为(3,4),将OA绕原点O逆时针旋转
得到OA1则点A1的坐标为( )
A.(-4,3) B.(-3,4) C.(3,-4) D.(4,-3)
8.请你用一个圆,一个三角形,一条线段,设计一个中心对称图形,并说明你所
摆出的图案的含义.
9.已知,图A、图B分别是正方形网格上的两个中心对称图形,网格中最小的正
方形面积为一个平方单位,则图A的面积为 ,图B的面积为 ;
你能在图C的网格上画出一个面积为8个平方单位的中心对称图形吗?
图A 图B 图C
10.如图,△ABC中,AD是中线,△ACD旋转后能与△EBD重合
①旋转中心是哪一点?②旋转了多少度?③如果M是AC的中点,那么经过上述旋
转后,点M转到了什么位置?
11.分析所给图形的形成过程.
12.在等腰三角形ABC中,∠C=,BC=2,如果以AC的中心O为旋转中心,
将这个三角形旋转1800,点B落在B1处,求点B1与点B(原来的位置处)的距离.
13.如图,点O是矩形ABCD的对称中心,过O点任作直线l,过B作BE⊥l于E.过D作DF⊥l
于F,求证:BE=DF.
第31课 图形的相似
1.如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则图中共有相似三角形( )
A.4对 B.5对 C.6对 D.7对
第1题图 第2题图 第3题图
2.如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于D、E,若AD=4,BD=2,则DE:BC的值为( )
A.15 B.2 C. D.
3.如图,在平行四边形ABCD中,E为DC边的中点,AE交BD于点O,若=9,则等于( )
A.18 B.27 C.36 D.45
4.如图,△ABC中,AE⊥BC于E,D为AB边上一点,如果BD=2AD,CD=8,sin∠BCD=,那么AE的值为( )
A.3 B.6 C.7.2 D.9
第4题图 第5题图 第6题图
5.如图,梯形ABCD的对角线交于点O,有以下四个结论:①△AOB∽△COD;②△AOD∽△ACB;③: =DC:AB;④=,其中始终正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图,要使△ACD∽△ABC,只需添加条件 (只要写出一个合适的条件即可).
7.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)6米的点A处,沿DA所在直线行走14米到点B时,人影长度变长 米
A D
B/
B M C
第7题图 第8题图 第9题图
8.矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、D为顶点的三角形与△ABM相似,则这样的点有 个.
9.如图,△ABC与△DEF是位似图形,相似比为2:3,已知AB=4,则DE的长等于 .
10.如图,AC⊥AB,BE⊥AB,AB=10,AC=2,用一块三角尺进行如下操作,将直角顶点P在线段AB上滑动,一直角边始终经过点C,另一直角边与BE相交于点D,若BD=8,则AP的长为 .
11.在方格纸中,每个小格的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在如图5×5的方格纸中,以A、B为顶点作格点三角形,与△ACB相似(相似比不能为1),则另一个顶点C的坐标为 米.
第10题图 第11题图 第12题图
12.如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积为S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第8个正方形的面积S8= .
13.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连结AE,图中有无相似三角形?若有,请写出,并对其中一对加以证明,若没有,请证明理由.
14.如图,PAB、PCD是⊙O的两条割线,AB是⊙O的直径,AC∥OD,
求证:(1)CD= (先填后证);
(2)若=,试求的
第32课 锐角三角函数(解直角三角形)
1.已知为锐角,且,则= .
2.在Rt△ABC中,∠C=90°,,AC=4,则BC= .
3.已知:如图,在△ABC中,∠A=30°,, ,则AB的长为 .
4.一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处(如图).上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里.(结果保留根号)
5.RtABC中,∠C=,∠A∶∠B=1∶2,则sinA的值( )
A. B. C. D.1
(第9题)
6.如图,在平面直角坐标系中,已知点A(3,0),点B(0,-4)则等
于( )
A. B. C. D.
7.·的值是( )
A.2-3 B. C.2- D.-1
8.在△ABC中∠C=900,a,b,c分别是∠A,∠B,∠C的对边,且,则的值( )
A. B. C. D.
9.在直角三角形中,各边的长度都扩大原来的m倍,则锐角A的各三角函数值( )
A.都扩大到m倍 B.都扩大到(m+1)倍 C.不变 D.不能确定
10.如图,两条宽度都是1的纸条,交叉重叠放在一起,则重叠部分的面积为( )
A. B. C. D.
11.沿坡角为30°的斜面前进100米,则上升的高度为( )
A. m B.m C.50 m D.50m
12.计算:
13.计算: 第10题图
14.如下图所示,在△ABC中,∠C=90°,D是AC边上一点,且,,求和.
15.某片绿地的形状如图,其中,ABBC,ADCD,AB=200米,CD=100米,求AD,BC的长.
16.某校的教室A位于工地O的正方向,且OA=200米,一部拖拉机从O点出发,以每秒5米的速度沿北偏西方向行驶,沿拖拉机的噪声污染半径为130米,试问教室A是否在拖拉机噪声污染范围内?若不在,请说明理由,若在,求出教室A受污染的时间有几秒?(已知 )
第33课 图形的变换与坐标的关系
1.在直角坐标系中,点P(-5,8)关于x轴对称点P1的坐标是 ;点P(-5,8)关于y轴对称点P2的坐标是 ;点P(-5,8)关于原点对称点P3 的坐标是 .
2.设点M(x , y)在第三象限,=2,=3,则点M关于原点对称的点N的坐标是
.
3.若点A(m,3)在函数y=5x+3的图像上,则点A关于原点对称的点B的坐标是 .
4.若点A关于y轴对称的点的坐标是(,-), 那么点A关于x轴对称的点C的坐标是 .
5.若点P关于原点对称的点P1的坐标是(,2),那么点P关于x轴对称的点P2的坐标是 .
6.若点P(m , n)其中m>0、n>0关于原点对称的点P1的坐标是 ,关于x轴对称的点P2的点的坐标是 ,关于y轴对称的点P3的坐标是 ,关于直线y=x对称的点P4的坐标是 ;关于直线y=-x对称的点P5的坐标是 ;
7.若点A(,3)与点B(,-3)关于原点对称, 则a= ,b= .
8.若直线y=-x+3的图像与抛物线y=x2 -3x-12的交点坐标是 ,它们关于y轴对称的点的坐标是 .
9.若直线y=3x+2的图像与直线y=-x+2的交点坐标是A,则点A关于y轴对称点B的坐标是 .
10.已知,点A(a+2 , b-4)与点A(-b,-3a)关于原点对称,则2006×2007= .
11.已知平面直角坐标系上的三个点O(0,0),A(-1,1),B(-1,0),将△ABO绕点O按顺时针方向旋转135,则点A、B的对应点A1、B1的坐标分别是A1( , ),B1( , ).
12.在△ABC中A(3,-1)、B(2,-1)、C(0,2) ,若将△ABC绕点C顺时针旋转90后得到△A1B1C1,则点A1的对应点的坐标是 .
13.已知,点P(x , y)的坐标满足+=0,则点P关于y轴对称的点P1在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
14.设M(x , y) 点在第三象限,且=3, =2,则M点关于y轴的对称点的坐标是( )
A.(3,2) B.(-3,-2) C.(-3,2) D.(3,-2)
15.点M(-,1)绕原点旋转60后的坐标是( )
A.(-,-1) B.(,1) C.(,-1) D.(-,-1)或(0,2)
16.如图1,在平面直角坐标系中, △ABC为等边三角形, 其中点A、B、C的坐标分别为(3,1)、(3,3),(3-,2),现以y轴为对称轴作△ABC的对称图形,得△A1B1C1,再以x轴为对称轴作的对称图形,得△A2B2C2
⑴直接写出A2 、B2两点的坐标;
⑵是否能通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请直接写出绕哪一点旋转多少度;你若认为不能, 请作出否定的回答(不必说明理由);
⑶设当△ABC的位置发生变化时,△A2B2C2、△A1B1C1与△ABC之间的对称关系始终保持不变:
①当△ABC向下平移多少个单位时,A1B1C1与A2B2C2完全重合?并直接写出此时C点的坐标;
②将△ABC绕点A顺时针针旋转α (0≤α≤180),使△A1B1C1与A2B2C2完全重合,此时α的值为多少?点C的坐标又是什么?
第五单元 图形的变换检测卷
(满分100分,时间60分钟)
一.填空题(每题3分,共36分)
1.如图,四边形ABCD是正方形,△ADE旋转后能与△ABF重合,则(1)旋转中心是 , 按 方向旋转了 度;(2)若连结EF,那么△AEF是 三角形.
2.如图,把两个大小完全相同的矩形拼成“L”形,则∠FAC= ,∠FCA= .
第1题图 第2题图 第3题图
3.如图,△ABC绕点C旋转到△,且与AC垂直,则∠= (填写角度)
4.如图,ABCD是一张矩形纸片,点O为矩形对角线的交点.直线MN经过点O交AD于M,交BC于N.先沿直线MN剪开,并将直角梯形MNCD绕点O旋转 度后,恰与直角梯形NMAB完全重合;再将重合后的直角梯形MNCD以直线MN为轴翻转后所得到的图形是下列中的 .(填写正确图形的代号)
5.已知,且,则.
6.如图,D、E、F分别是△ABC各边的中点,则△DEF与△ABC面积的比是 .
第4题图 第6题图 第7题图
7.如图,四边形ABCD与四边形EFGH相似,则∠H= .
8.要把一个三角形的面积扩大到原来面积的4倍,而它的形状不变,那么它的边长要扩大到原来的 倍.
9.如图,已知两座高度相等的建筑物AB、CD的水平距离BC=60米,在建筑物CD上有一铁塔PD,在塔顶P处观察建筑物的底部B和顶部A,分别测得俯角,建筑物AB的高等于 .(计算过程和结果一律不取近似值)
第9题图 第10题图 第11题图 第12题图
10.如图,AD∥EF∥BC,则图的相似三角形共有 对.
11.如图,正方形ABCD中,E是AD的中点,BM⊥CE,AB=6, 则BM= .
12.如图,ΔABC中,∠A=∠DBC, BC= ,SΔBCD∶SΔABC=2∶3, 则CD= .
二.选择题(每题4分,共36分)
13.下面四个图案中,既包含图形的旋转,又有图形的轴对称的设计是( )
A B C D
14.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
A. B. C. D.
15.如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且,则CE的长是( )
A. B. C. D.
第14题图 第15题图 第21题图
16.以下现象:(1)水管里水的流动(2)打针时针管的移动(3)射出的子弹(4)火车在笔直的铁轨上行驶,其中是平移的是( )
A.(1)(2) B.(1)(3) C.(2)(3) D.(2)(4)
17.在5×5方格纸中将图(1)中的图形N平移后的位置如图(2)中所示,那么正确的平移方法是( ).
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
18.下列判断中,正确的是( ).
A.两个平行四边形一定相似 B.两个矩形一定相似
C.两个菱形一定相似 D.两个正方形一定相似
19.把一个矩形对折成两个相同的小矩形,如果这两个小矩形与原矩形相似,那么原矩形的长与宽的比值是( ).
A. B. C. D.
20.一个三角形的两边之比为a:b=3:1,则这两边上的高的比ha:hb为( )
A.3:1 B.1:3 C.9:1 D.1:9
21.如图,在平行四边形ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
A.4:5 B.3:5 C.4:9 D.3:8
三.解答题(22~24题,每题6分,25题10分)
22.在旷野上,一个人骑着马从A到B,半路上他必须在河边饮马一次,如图,他应该如何来选择饮马点P,才能使所走的
路程AP+PB最短呢?
23.如图网格中有一个四边形和两个三角形(各少一边).
(1)请你画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,
请写出这个整体图形对称轴的个数,这个整体图形至少
旋转多少度与自身重合?
24.如图,某船在A处测得灯塔B在北偏东30°方向,现该船从A处出发以每小时24海里的速度向正北方向航行15分钟到达C处,在C处测得灯塔B在北偏东45°的方向,求A到灯塔B的距离(结果取准确值)
25.如图,等腰梯形ABCD中,AD//BC,AD=3cm,BC=7cm, ∠B=60°,P为下底BC上一点,不与BC重合,连接AP,过P点作PE交DC于E,使得∠APE=∠B.
(1)求证:△ABP∽△PCE
(2)求等腰梯形的腰AB的长
(3)在底边BC上是否存在一点P,使得DE:EC=5:3?如果存在,求BP的长,如果不存在,请说明理由.
空间与图形综合检测卷(一)
(总分100分,时间60分钟)
一.选择题(每题3分)
1.如图是由几个相同的小正方形搭成的集合体的
三种视图则搭成这个几何体的小正方形的
个数为( )
A.3 B.4 C.5 D.6 俯视图 主视图 左视图
2.如图,⊙O的直径CD过弦EF的中点G,∠EOD=40,则∠DCF 等于( )
A.80 B.50 C.40 D.20
3.如图,B是线段AC的中点,过C点的直线l与AC成60的角.
在直线l上取一点,使得∠APB=30 则满足条件的点P 的个数是( )
A.3个 B.2个 C.1个 D.不存在
4.如图,在Rt△ABC中∠ACB=90 ,CD⊥AB于点D,已知AC=,BC = 2那么
Sin∠ACD= ( )
A. B. C. D.
5.如图, 小丽要制作一个圆锥模型,要求圆锥的母线长为10㎝那么小丽要制作的这个圆锥模型的侧面展开图的圆心角度数是( )
A.150 B.200 C.180 D.240
6.在矩形ABCD中,对角线AC、BD相交于点G、E为AD的中点,连接BE交AC于F, 连接FD.若∠BFA=90 则下列四对三角形(1)△BEA与△ACD ;(2)△FED与 △DEB;
(3)△CFD与△ABG; (4)△ADF 与△CFB.其中相似的为( )
A.(1)(4) B.(1)(2) C.(2)(3)(4) D.(1)(2)(3)
7.一个三角形的两边长为3和6第三边的边长为方程(x-2)(x-4)=0 的根,则这个三角形的周长是( )
A. 11 B. 11或13 C. 13 D. 11或13
8.将一个正方形纸片依次按图(1)图(2)方式对折然后沿着图(3)中的虚线裁剪.最后将图(4)的纸片再展开铺平.所得到图案是( )
图(1)(向上对折) 图(2)(向右对折)图(3)图(4)
A. B. C. D.
9.如图△ABC与△ABC关于直线l对称.将△ABC 向右平移得到△ABC由此得出下列判断:(1)AB=AB,(2)∠A=∠A,(3)AB=AB其中正确的是( )
A .(1) (2) B.(2) (3)
C .(1) (3) D.(1) (2) (3)
10.如图,一块含有30角的直角三角板ABC,在水平桌面
上绕点C按顺时针旋转到△ABC的位置若的BC长为15㎝,
那么顶点A从开始到结束所经过的路径长为( )
A.10∏㎝ B.10∏㎝ C.15㎝ D.20 ∏㎝
11.如图,在Rt△ABC中∠C=90,A C=4㎝,BC=6㎝ 动点P从点C沿C A,以1㎝/s的速度向点A运动.同时动点Q从点C沿CB,以2㎝/s的速度向点B运动,则运动过程中所构成的△CPQ的面积y(㎝)与运动时间x(s)之间的函数图像大致是( )
12.如图, ⊙O内切于△ABC,切点为D、E、F,若∠B=50,∠C=60 连结OE、OF、DE、DF,则∠EDF等于( )
A . 45 B . 55 C. 65 D .70
二.填空题(每题3分)
1.如图,PQ是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大
小等于 度.
第1题图 第3题图 第4题图
2.将点A(3,1)绕原点顺时针旋转90到点B.则B点的坐标是 .
3.如图是由9个等边三角形拼成的六边形, 若已知中间的小等边三角形的边长是a,则六边形的周长是 .
4.如图,在直角坐标系中,右边的图案是由左边的图案经过平移得到的, 左图案中左右眼睛的坐标分别是(-4,2),(-2,2)右图案中左眼的坐标是(3,4)则右图案中右眼的坐标是 .
5.如图,在△ABC中,AC= BC= 2,∠ACB=90,D是
边BC的中点,E是AB边上一动点, 则EC+ED的
最小值是 .
6.如图, 把矩形纸片OABC放入平面直角坐标系中,使 OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿着OB折叠,使点A落在点A的位置上.若OB=,tan∠BOC=,则点A的坐标为 .
三.解答题
1.如图, A、D、F、B在同一条直线上,AD=BF,AE=BC, 且AE∥BC.
求证:(1)△AEF≌△BCD;(2)EF∥CD.(8分)
2. 如图,图中的小方格都是边长为1的正方形,△ABC与△A1B1C1是关于点O为位似中心的为似图形,它们的顶点都在校正方形的顶点上.
(1) 画出位似中心点O;
(2) 求出△ABC与△A1B1C1的位似比;
(3) 以点O为位似中心,再画一个△A1B1C1,使得它与△ABC的位似比等于1.5.(9分)
3. 如图,某校九年级3班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚点A测得山腰上一点D的仰角为30,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45,山腰点D的俯角为60.请你帮助他们计算出小山的高度(计算过程和结果都不去近似值).(8分)
4. 如图, 在平行四边形ABCD中,∠DAB=60,点E、F分别在CD、AB的延长线上,且AE=AD,CF=CB.
(1)求证:四边形AFCE是平行四边形;
(2)若去掉已知条件的“∠DAB=60”,
上述的结论还成立吗?若成立,请
写出证明过程;若不成立,请说明理由.(9分)
5.在⊙O的内接△ABC中,AB+AC=12,AD⊥BC垂足为D,且AD=3,设⊙O的半径为y, AB的长为x.
(1)求y与x的函数关系式;
(2)当AB的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积.(9分)
6.如图,点T在⊙O上,延长⊙O的直径AB交TP于P,若PA=18,PT=12,PB=8.
(1)求证:△PTB∽△PAT;(2)求证:PT为⊙O的切线.
(3)在AT弧上是否存在一点C,使得BT=8TC?若存在,请证明;若不存在,请说明理由.(10分)
7.如图所示,在平面直角坐标系中,四边形OABC是等腰梯形,BC∥OA,OA=7,AB=4,∠COA=60,点P为x轴上的一个动点,点P不与点O、点A重合.连结CP,过点P作PD交AB于点D.
(1)求点B的坐标;
(2)当点P运动什么位置时,△OCP为等腰三角形,求这时点P的坐标;
(3)当P运动什么位置时,使得∠CPD=∠OAB,且=,求这时P的坐标.(11分)
8.如图,已知P为∠AOB的边OA上的一点,以P为顶点的∠MPN的两边分别交射线OB于M、N两点,且∠MPN=∠AOB=α(α为锐角).当∠MPN以点P为旋转中心,PM边与PO重合的位置开始,按逆时针方向旋转(∠MPN保持不变)时,M、N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.若Sinα=、OP=2.
(1)当∠MPN旋转30(即∠OPM=30)时,求点N移动的距离;
(2)求证:△OPN∽△PMN;
(3)写出y与x之间的关系式;
(4)试写出S随x变化的函数关系式,并确定S的取值范围.
(12分)
第五单元 图形的认识
第29课 图形的轴对称答案
1.D 2.A 3.C 4.C 5.B 6.D 7.B 8.A 9.B 10.C
11.略 12.略
第30课 图形的平移与旋转答案
1.(1)(4)(6)(8);(2)(3)(7), 2. 80o;5cm2;4cm;8cm 3.①④;②⑤;③ 4. B 5. B 6. A 7. D 8. 略。 9.12,12,略 10.D点,180o,M为BE的中点。 11.略 12.连接BB1,则O在BB1上,在Rt BOC中,BC=2,OC=1,
所以OB=,所以B1B=2OB=2。 13.连接BD,因为矩形ABCD为中心对称图形,O为对称中心,所以O在BD上,且OB=OD,又因为∠BEO=∠DFO=90o,∠BPE=∠DOF,
所以ΔBEO≌ΔDFO,所以BE=DF。
第31课 图形的相似答案
1.B 2.C 3.C 4.D 5.C 6.∠ADC=∠ACB (∠ACD=∠ABC)
7.3.5米 8.2 9.6 10.2或8 11.(4,4)或(5,2) 12.128
13.有 △ADE∽△AEC,证明略 14.(1)CD=BD 证明略 (2) ,
第32课 锐角三角函数(含解直角三角形)答案
1. 2. 3. 4.5.A 6.C 7.A 8.B 9.C 10.C 11.C 12.解:原式=1 13.解:原式=1
14.解:在Rt△CDB中,,,∴.
在Rt△ABC中,,,∴.
15.解:Rt△ABC中
∠E=900-∠A=900-600=300
RT△CDE中
16.解:由题意可知,OA=200米 作AB⊥OM于B,
教室A在噪音范围内
由题意知,在OM上取两点C、D,得AC=AD=130米
AB⊥OM 米
米 米
受污染时间为秒
第33课 图形的变换与坐标的关系答案
1.(-5,-8),(5,8),(5,-8)。 2.(2, 8)、(2, 2)。 3.(0,-3)。
4.(-,)。 5.(-,2 )。 6.(-m,-n),(m,-n),(-m,n),(n,m),(-n,-m)。 7. 2 ,2。 8.(-3,6)、(5,-2),(-5,-2)、(3,6)。
9.(0,2)。 10. 2007。 11. 0 。 12.(-1,-3) 13.C 14. D 15. D 16.(1)(3,-1),(-3,-3) (2) 能 绕点O旋转180 ① 2 (3-,0) 180 (3+,0)。
第五单元 图形与变换检测卷答案
一.填空题
1.A 顺时针 90度 等腰直角三角形 2.90度,45度 3.55度
4.180度,D 5.x=6,y=10 6.1:4 7.67度 8.2 9.60-20
10.3 11. 12.
二.选择题:
13.D 14.B 15.D 16.D 17.C 18.D 19.C 20.B
21.C
空间与图形综合检测卷(1)答案
一.选择题:1.B 2.D 3.B 4.A 5.B 6.D 7.C 8.D 9.B 10.D 11.C 12.B
二.填空题:1. 120 2. (1,-3) 3. 30 a 4. (5,4) 5. 6. (-,)
三.解答题
1.略 2. (1).略 (2). 位似比为 1:2 (3). 略 3. 90(+1)米 4. (1) 略 (2)还成立.证明略
5. (1).y=-x2+2x. (2).当x=6时y取最大值6.⊙O的最大面积为36π.
6.(1)证明:在△PBT和△PTA中,∵∠BPT=∠TPA,∵==,= = ,
∴ = ∴△PBT∽△PTA (2).连结OT,.∵OB=OT∴∠OBT=∠BTO.由(1)得∠PTB=∠PAT.∵AB是直径,∴∠BTA=900,∴∠A+∠ABT=900,∴∠OTB+∠BTP=900,∴PT是⊙O的切线. (3)解:∵∠ABT=∠P+∠PTB,∴∠ABT>∠P.过B作BC交⊙O于C,使∠BCT=∠P. 由(1)得∠PTB=∠PAT= ∠BCT∴△PBT∽△BTC∴= , 又PB=8, ∴BT2=8TC 存在一点 C 使得BT2=8TC.
7. (1);过C作CD⊥OA于A,BE⊥OA于E 则△OCD≌△ABE,四边形CDEB为矩形
∴OD=AE,CD=BE∵OC=AB=4,∠COA=60°∴CD=,OD=2 ∴CB=DE=3
∴OE=OD+DE=5 ∵BE=CD=∴B(5,)
(2)∵∠COA=60°,△OCP为等腰三角形∴△OCP是等边三角形
∴OP=OC=4 ∴P(4,0)即P运动到(4,0)时,△OCP为等腰三角形
(3)∵∠CPD=∠OAB=∠COP=60°∴∠OPC+∠DPA=120°又∵∠PDA+∠DPA=120°
∴∠OPC=∠PDA∵∠OCP=∠A=60°∴△COP∽△PAD ∴
∵,AB=4 ∴BD= ∴AD= 即 ∴
得OP=1或6∴P点坐标为(1,0)或(6,0)
8.解 : (1)点N移动的距离为2. (2).略 (3) y= (4)0≤S<
B
A
C
D
E
F
O
A
B
C
D
E
F
l
A
B
x
y
O
A(3,0)
0
x
y
B(0,-4)
A
B
C
D
图图1 图2
第3题图
第4题图
第5题图
第6题图
A
B
C
D
E
北
东
O
A
M
B
C
D
同课章节目录
