统计与概率[下学期]
图片预览




文档简介
三 统计与概率
第六单元 统计与概率
第34课 数据的收集、整理、描述
1.某商场地“十·一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31 = 465(万元),你认为这样的推断是否合理?答:. .
2.已知数据35,31,33,35,37,39,35,38,40,39,36,34,35,37,36,32,34,35,36,34在列频数分布表时,如果取组距为2,那么应分成 组。
分 组 频数 频率
13.5~15.5
15.5~17.5
17.5~19.5 8 0.4
19.5~21.5
21.5~23.5 2 0.1
合 计
3.某专业养鱼户去年在鱼塘中投入一批鱼苗,为了了解鱼苗的长势,从中捞取20条,测得其长度如下(单位:cm):
19 14 17 16 18 15 19 22 21 16 18
20 23 17 20 20 19 19 18
⑴填写表中的空白栏
⑵由该表可知,长度小于18cm的鱼苗所占的百分
比为
⑶在这批鱼苗中,有80%的鱼苗长度
在 cm到 cm之间。
4.下列调查中,调查方式选择正确的是( )
A.为了了解100个学生的身高情况,选择全面调查;
B.为了了解某公园全年的游客流量,选择全面调查;
C.为了了解生产的50枚炮弹的杀伤半径,选择全面调查;
D.为了了解一批袋装食品是否有防腐剂,选择全面调查。
5.为了了解一批电视机的寿命,从中抽取100台电视机进行试验,这个问题的样本是( )
A.这批电视机; B.这批电视机的寿命;
C.抽取的100台电视机的寿命; D.100.
6.某旅游团的所有30名游客按年龄分成3组,其中年龄在20~40岁组内有9名,那么这个小组的频率是( )
A.3.3 B.0.3 C.0.9 D.0.45
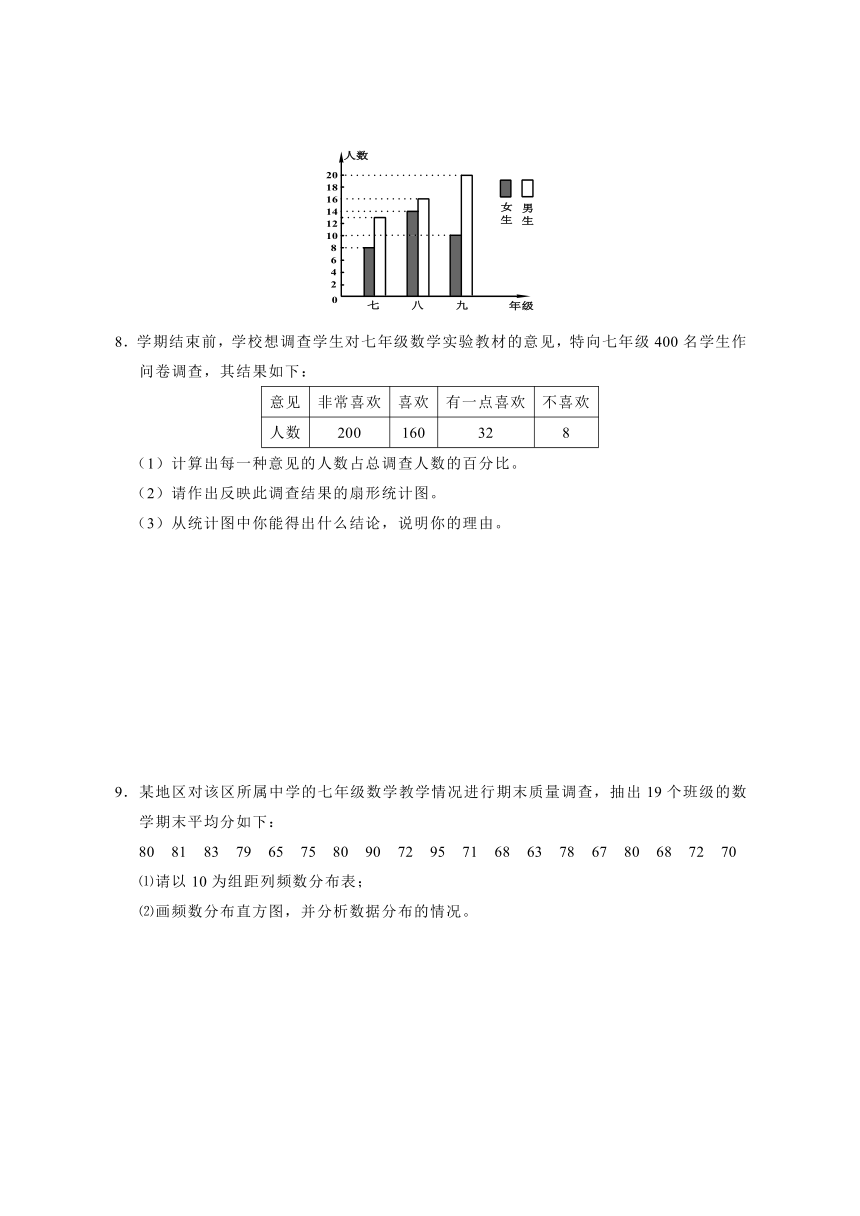
7.如图,所提供的信息正确的是( )
A.七年级学生最多;
B.九年级的男生是女生的两倍;
C.九年级学生女生比男生多;
D.八年级比九年级的学生多。
8.学期结束前,学校想调查学生对七年级数学实验教材的意见,特向七年级400名学生作问卷调查,其结果如下:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 200 160 32 8
(1)计算出每一种意见的人数占总调查人数的百分比。
(2)请作出反映此调查结果的扇形统计图。
(3)从统计图中你能得出什么结论,说明你的理由。
9.某地区对该区所属中学的七年级数学教学情况进行期末质量调查,抽出19个班级的数学期末平均分如下:
80 81 83 79 65 75 80 90 72 95 71 68 63 78 67 80 68 72 70
⑴请以10为组距列频数分布表;
⑵画频数分布直方图,并分析数据分布的情况。
第35课 数据的分析
1.对于数据组3,3,2,3,6,3,6,3,2中,众数是 ______;平均数是______;极差是_________;中位数是_________.
2.数据3,5,4,2,5,1,3,1的方差是_________.
3.某学生7门学科考试成绩的总分是560分,其中3门学科的总分是234分,则另外4门学科成绩的平均分是_________.
4.在n个数中,若x1出现f1次,x2出现f2次,…xk出现fk次,且f1+f2+…+fk=n,则它的加权平均数=___________________________________________.
5.一组数据同时减去80,实得新的一组数据的平均数为2.3,那么原数据的平均数为_________.
6.8个数的平均数12,另4个数的平均数为18,则这12个数的平均数为( ).
A.12 B.18 C.14 D.12
7.甲、乙两个样本的容量相同,甲样本的方差为0.102,乙样本的方差是0.06,那么( ).
A.甲的波动比乙的波动大 B.乙的波动比甲的波动大
C.甲、乙的波动大小一样 D.甲、乙的波动大小无法确定
8.在某次数学测验中,随机抽取了10份试卷,其成绩如下:
85,81,89,81,72,82,77,81,79,83
则这组数据的众数、平均数与中位数分别为( ).
A.81,82,81 B.81,81,82
C.83,81,77 D.81,81,81
9.为了了解学校开展“尊敬父母,从家务事做起”活动的实施情况,该校抽取初二年级50名学生,调查他们一周(按七天计算)的家务所用时间(单位:小时),得到一组数据,并绘制成下表,请根据该表完成下列各题:
(1)填写频率分布表中未完成的部分;
(2)这组数据的中位数落在什么范围内;
(3)由以上信息判断,每周做家务的时间不超过1.5小时的学生所占的百分比.
10.小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,可奶奶经营不善,经常有品种的牛奶滞销(没卖完)或脱销(量不够),造成了浪费或亏损,细心的小红结合所学的统计知识帮奶奶统计了一个星期牛奶的销售情况,并绘制了下表:
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高?
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定?
(3)假如你是小红,你会对奶奶有哪些好的建议.
第36课 概 率 初 步
1.两次投掷硬币,都是正面向上的概率是 .
2.“太阳每天从东方升起”这是一个 事件.(填“确定”或“不确定”)
3.有四张不透明的卡片为2, , ,除正面的数不同外,其余都相同,将它们背面朝上洗匀后,从中随机抽取一张卡片,抽到写有无理数卡片的概率 .
4.从两副拿掉大、小王的扑克牌中各抽取一张牌都是红桃的概率为 .
5.在一个不透明口袋中,装有若干个颜色不同,其余都相同的球,如果口袋中装4个红球且摸到红球的概率为,则口袋中球的总数是 .
6.图中的圆被六等分,他是可以自由转动的转盘,转动转盘,当转盘停止后,指针指向红色区域的概率 .
7.一个春光明媚的早晨,小明想去乡下姥姥家,享受美丽的“田园风光”,他匆匆来到就近的候车亭,这时他才知道10分钟一辆班车,2分钟内他能乘上班车的概率 .
8.飞蛾有较强的趋光性,夏夜一只可爱的小飞蛾想从玻璃窗外飞入,只有1m的窗户上有15cm15cm的一小块破洞,它能飞入的概率是 .
9.同时抛掷2枚一元的硬币,菊花图案都朝上的概率是( )
A. B. C. D.
10.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. D.
11.一个袋子里装有一双红色,一双绿色手套,两双手套除颜色不同外,其他完全相同,随机地从中摸出两只恰好是一双的概率( )
A. B. C. D.
12.在一个不透明的布袋中,红色,黑色,白色的玻璃球共有40个,除颜色外其他完全相同,小李通过多次模球试验后发现其中摸到红球,黑球的频率稳定在15%和45%,则口袋中白球的个数可能是 ( )
A.6 B.16 C.18 D.24
13.下列说法正确的是( )
A.一颗质地均匀的骰子连续投掷2000次,其中投掷5点的次数最少,则2001次一定投掷出5点;
B.某种彩票中奖率是1%,则买100张这种彩票一定会中奖;
C.天气预报说明明天下雨的概率是50%,所以明天将有一半时间下雨;
D.抛掷一枚图针,针尖触地和针尖朝上的概率不相等。
14.蚂蚁从甲地到乙地,共有三条路径,其中丙处有路障,则蚂蚁遇到路障的概率( )
A.1 B. C. D.0
15.田鼠喜欢歇身在土质松软的洞穴里,下图中空心洞穴为松土质洞穴,若田鼠从甲地出发,随机顺一条路寻找洞穴,求它一次就找到合适洞穴的概率。
16.如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可以使小灯泡发光。
(1)任意闭合其中一个开关,则小灯泡发光的概率是多少?
(2)任意闭合其中两个开关,请用画树状图或列表法求出小灯泡发光的概率。
17.某学校有A,B两个餐厅,甲,乙两名学生各自随机选择其中一个餐厅用餐:
⑴求甲、乙两名学生在同一餐厅用餐的概率;
⑵求甲、乙两名学生中至少有一名学生在B餐厅就餐的概率;
⑶如果餐厅数为A、B、C三个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,求甲、乙两名学生在同一餐厅用餐的概率;
(4)餐厅数为M个餐厅,N名学生各自随机选择其中一个餐厅用餐,求N名学生在同一餐厅用餐的概率。
18. 你喜欢玩游戏吗?小明、小刚、小军、小华四个小朋友一起玩掷骰子游戏,每只骰子都是一个正方体,每个面上有不同的点子数,点子数分别是1、2、3、4、5、6,一次投掷两枚,向上一面的点数和为2、6、10时小明胜,和为3、7、11时小刚胜,和为4、8、12时小军胜,和为1、5、9时小华胜。你认为这个游戏对四个小朋友公平吗?请你说明理由。
第六单元 统计与概率检测卷
(总分100分,时间60分钟)
一.选择题:(3分×9=27分)
1.国家统计局发布的统计公报显示:2001到2005年,我国GDP增长率分别为8.3%,9.1%,10.0%,10.1%,9.9%。经济学家评论说:这五年的年度GDP增长率之间相当平稳,从统计学的角度看, “增长率之间相当平稳”说明这组数据的( )比较小。
A.中位数 B.标准差 C.平均数 D.众数
2.某服装销售商在进行市场占有率的调查时,他最应该关注的是( )
A.服装型号的平均数 B.服装型号的众数
C.服装型号的中位数 D.最小的服装型号
3.图中甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
4.为了了解我市6000名学生参加的初中毕业会考 数学考试的成绩情况,从中抽取了200多考生的成绩进行统计,在这个问题中,下列说法:①这6000名学生的数学会考成绩的全体是总体;②每个考生是个体;③200名考生是总体的一个样本;④样本容量是200。其中说法正确的个数是( )
A.4个 B.3个 C.2个 D.1个
5.下列事件中确定事件是( )
A.掷一枚均匀的硬币,正面朝上
B.买一注福利彩票一定会中奖
C.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球
D.掷一枚六个面分别标有1,2,3,4,5,6的骰子,骰子停止转动后奇数点朝上
6.在元旦游园晚会上有一个闯关活动:将5张背面完全一样正面分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关,那么一次过关的概率是( )
A. B. C. D.
7.有2名男生和2名女生,王老师要随机地、两两一对地为他们排座位,一男一女排在一起的概率是( )
A. B. C. D.
8.现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6)。用小莉掷A立方体朝上的数字为x,小明掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为( )
A. B. C. D.
9.以下说法合理的是( )
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%;
B.抛掷一枚普通正六面体骰子,出现6的概率是1/6的意思是每6次就有1次掷得6;
C.某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖;
D.在一次试验中,甲乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51.
二.填空题:(3分 ×10=30分)
10.把一组数据中的每一个数据都减去80,得一组新数据,若求得新一组数据的平均数是1.2,方差是4.4,则原来一组数据的平均数和方差分别为____________.
11.王老汉为了与客户签订购销合同,对自己的鱼塘中鱼的总重量进行估计,第一次捞出100条,称得重量为184kg,并将每条鱼作上记号放入水中;当它们完全混合于鱼群后,又捞出200条,称得重量为416kg,且带有记号的鱼有20条,王老汉的鱼塘中估计有鱼____________条,共重____________kg.
12.甲乙两人进行射击比赛,在相同条件下各射击10次,他们的平均成绩均为7环,10次射击成绩的方差分别是:S甲2=3,S乙2=1.2;成绩较为稳定的是____________.(填“甲”或“乙”)
13.从甲、乙、两三个厂家生产的同一种产品中,抽出8件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
甲:3,4,5,6,8,8,8,10
乙:4,6,6,6,8,9,12,13
丙:3,3,4,7,9,10,11,12
三个厂家的广告中都称该种产品的使用寿命是8,根据调查结果判断,厂家在广告中分别运用了平均数、众数、中位数中哪一种集中趋势的特征数;
甲:____________,乙:____________,丙:____________.
14.已知一组数据:-2,-2,3,-2,x,-1,若这组数据的平均数是0.5,则这组数据的中位数是____________.
15.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小张和小李两人中新手是____________.
第15题 第16题
16.如图所示,要把北京奥运的5个吉祥物“福娃”放在展桌上,有2个位置如图已定,其他3个“福娃”在各种不同位置放置的情况下,“迎迎”和“贝贝”的位置不相邻这一事件发生的概率为____________.
17.田忌赛马是一个为人熟知的故事,传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强。有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜,看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强。如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是____________.
18.抛掷两枚分别标有1,2,3,4的四面体骰子,写出这个实验中的一个可能事件是____________;写出这个实验中的一个必然事件是____________.
19.小明和小尹按如下规则做游戏:桌面上放有5支铅笔,每次取一支或两支,由小明先取,最后取完铅笔的人获胜。如果小明获胜的概率为1,那么小明第一次应该取走_________支.
三.解答题:(共43分)
20.(8分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员 工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数名 1 3 2 3 24 1
每人月工资/元 21000 8400 2025 2200 1800 1600 950
请你根据上述内容,解答下列问题:
⑴该公司“高级技工”有__________名;
⑵所有员工月工资的平均数x为2500元,中位数为_______元,众数为________元;
⑶去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保管整数),判断y能否反映该公司员工的月工资实际水平。
21.(8分)根据北京市统计局公布的2000年、2005年北京市人口数据,绘制统计图表如下:
2000年、2005年北京市常住人口中受教育程度情况统计表(人数单位:万人)
年份 大学程度人数(指大专及以上) 高中程度人数(含中专) 初中程度人数 小学程度人数 其他人数
2000年 233 320 475 234 120
2005年 362 372 476 212 114
请利用上述统计图表提供的信息回答下列问题:
⑴从2000年到2005年北京市常住人口增加了多少万人?
⑵2005年北京市常住人口中,少儿(0-14岁)人口约为多少万人?
⑶请结合2000年和2005年北京市常住人口受教育程度的状况,谈谈你的看法。
22.(9分)某报社为了解读者对本社一种报纸四个版面的喜欢情况,对读者作了一次问卷调查,要求读者选出自己最喜欢的一个版面,将所得数据整理后绘制成了如图的条形统计图;
⑴请写出从条形统计图中获得的一条信息;
⑵请根据条形统计图中的数据补全扇形统计图(要求:第二版与第三版相邻),并说明这两幅统计图各有什么特点?
⑶请你根据上述数据,对该报社提出一条合理的建议。
第22题 第23题
23.(9分)有一块表面是咖啡色、内部是白色、形状是正方体的烤面包。小明用刀在它的上表面、前表面和右侧表面沿虚线各切两刀,将它切成若干块小正方体形面包(如图)
⑴小明从若干块小面包中任取一块,求该块面包有且只有两个面是咖啡色的概率;
⑵小明和弟弟边吃边玩,游戏规则是:从中任取一块小面包,若它有奇数个面为咖啡色时,小明赢;否则,弟弟赢,你认为这样的游戏规则公平吧?为什么?如果不公平,请你修改游戏规则,使之公平。
24.(9分)小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,末掷入圈内不算,你来当裁判。
⑴你认为游戏公平吗?为什么?
⑵游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算非规则图形的面积呢?”。请你设计方案,解决这一问题。(要求画出图形,说明设计步骤、原理、写出公式)
三 统计与概率
第六单元 统计与概率
第34课 数据的收集、整理、描述答案:
1.不合理 2.5 3.⑴略 ⑵30% ⑶16~21 4.A 5.C 6.B 7.B
8.⑴50%;40%;8%;2% ⑵略 ⑶略 9.略
第35课 数据的分析答案
1.略 2.2.25 3.81.5分 4.略 5.82.3
6.C 7.A 8.D
9.(1)2,0.14,0.06,(2)1.05~1.55,(3)58%
10.(1)学生奶=3,酸牛奶=80,原味奶=40,金键酸牛奶销量高,
(2)12.57,91.71,96.86,金键学生奶销量最稳定,
(3)建议学生奶平常尽量少进或不进,周末可进几瓶.
第36课 概率初步答案
1. 2.确定 3. 4. 5.12 6. 7. 8.
9.C 10.A 11.A 12.B 13.D 14.C 15. 16. 、
17. 、、 、
18.不公平。小明为 ,小刚的概率为 , 小军为 ,小华的概率为
第六单元统计与概率检测卷 答案
一.选择题
1.B 2.B 3.D 4.C 5.C 6.D 7.D 8.B 9.D
二.填空题
10.81.2 , 4.4 11. 1000,2000 12.乙 13.众数, 平均数 ,中位数 14.
15.小李 16. 17. 18.朝上数字为2[答案不唯一] ,朝上数字≥1 19. 2
三.解答题
20.(1)16 (2)1700, 1600 (3)Y=(2500×50-21000-8400×3)÷46=1713
Y值是可以反映员工的月工资水平的
21.(1)1536-1382=154(万人)
(2)1382×10.2%=140.964(万人)
(3)大学程度人数比例逐渐提高(答案不唯一)
22.(1)参加调查人数为5000人(答案不唯一)(2)补图略,扇形图能清楚表示出喜欢各版面读者人数占所调查的总人数的百分比,条形图能清楚地表示出喜欢各版面的读者人数。(3)建议改进第二版的内容,提高文章质量。(答案不唯一)
23.(1) (2)1个面有8块,3个面有6块,所以小明赢的概为,弟弟赢的概为,所以不公平,应奇数面为咖啡色,小明得13分,反之,弟弟得14分。
24.(1)不公平,小红胜的机会为,小明胜的机会为。(2)设计一个矩形面积为s将不规则图形围起来,用石子随意向矩形中扔,扔在矩形中的次数m和不规则图中的次数n记下,如不规则图形面积为M,则M=s×()。画图略。
甲
乙
·丙
甲
D
A
B
C
第六单元 统计与概率
第34课 数据的收集、整理、描述
1.某商场地“十·一”长假期间平均每天的营业额是15万元,由此推算10月份的总营业额约为15×31 = 465(万元),你认为这样的推断是否合理?答:. .
2.已知数据35,31,33,35,37,39,35,38,40,39,36,34,35,37,36,32,34,35,36,34在列频数分布表时,如果取组距为2,那么应分成 组。
分 组 频数 频率
13.5~15.5
15.5~17.5
17.5~19.5 8 0.4
19.5~21.5
21.5~23.5 2 0.1
合 计
3.某专业养鱼户去年在鱼塘中投入一批鱼苗,为了了解鱼苗的长势,从中捞取20条,测得其长度如下(单位:cm):
19 14 17 16 18 15 19 22 21 16 18
20 23 17 20 20 19 19 18
⑴填写表中的空白栏
⑵由该表可知,长度小于18cm的鱼苗所占的百分
比为
⑶在这批鱼苗中,有80%的鱼苗长度
在 cm到 cm之间。
4.下列调查中,调查方式选择正确的是( )
A.为了了解100个学生的身高情况,选择全面调查;
B.为了了解某公园全年的游客流量,选择全面调查;
C.为了了解生产的50枚炮弹的杀伤半径,选择全面调查;
D.为了了解一批袋装食品是否有防腐剂,选择全面调查。
5.为了了解一批电视机的寿命,从中抽取100台电视机进行试验,这个问题的样本是( )
A.这批电视机; B.这批电视机的寿命;
C.抽取的100台电视机的寿命; D.100.
6.某旅游团的所有30名游客按年龄分成3组,其中年龄在20~40岁组内有9名,那么这个小组的频率是( )
A.3.3 B.0.3 C.0.9 D.0.45
7.如图,所提供的信息正确的是( )
A.七年级学生最多;
B.九年级的男生是女生的两倍;
C.九年级学生女生比男生多;
D.八年级比九年级的学生多。
8.学期结束前,学校想调查学生对七年级数学实验教材的意见,特向七年级400名学生作问卷调查,其结果如下:
意见 非常喜欢 喜欢 有一点喜欢 不喜欢
人数 200 160 32 8
(1)计算出每一种意见的人数占总调查人数的百分比。
(2)请作出反映此调查结果的扇形统计图。
(3)从统计图中你能得出什么结论,说明你的理由。
9.某地区对该区所属中学的七年级数学教学情况进行期末质量调查,抽出19个班级的数学期末平均分如下:
80 81 83 79 65 75 80 90 72 95 71 68 63 78 67 80 68 72 70
⑴请以10为组距列频数分布表;
⑵画频数分布直方图,并分析数据分布的情况。
第35课 数据的分析
1.对于数据组3,3,2,3,6,3,6,3,2中,众数是 ______;平均数是______;极差是_________;中位数是_________.
2.数据3,5,4,2,5,1,3,1的方差是_________.
3.某学生7门学科考试成绩的总分是560分,其中3门学科的总分是234分,则另外4门学科成绩的平均分是_________.
4.在n个数中,若x1出现f1次,x2出现f2次,…xk出现fk次,且f1+f2+…+fk=n,则它的加权平均数=___________________________________________.
5.一组数据同时减去80,实得新的一组数据的平均数为2.3,那么原数据的平均数为_________.
6.8个数的平均数12,另4个数的平均数为18,则这12个数的平均数为( ).
A.12 B.18 C.14 D.12
7.甲、乙两个样本的容量相同,甲样本的方差为0.102,乙样本的方差是0.06,那么( ).
A.甲的波动比乙的波动大 B.乙的波动比甲的波动大
C.甲、乙的波动大小一样 D.甲、乙的波动大小无法确定
8.在某次数学测验中,随机抽取了10份试卷,其成绩如下:
85,81,89,81,72,82,77,81,79,83
则这组数据的众数、平均数与中位数分别为( ).
A.81,82,81 B.81,81,82
C.83,81,77 D.81,81,81
9.为了了解学校开展“尊敬父母,从家务事做起”活动的实施情况,该校抽取初二年级50名学生,调查他们一周(按七天计算)的家务所用时间(单位:小时),得到一组数据,并绘制成下表,请根据该表完成下列各题:
(1)填写频率分布表中未完成的部分;
(2)这组数据的中位数落在什么范围内;
(3)由以上信息判断,每周做家务的时间不超过1.5小时的学生所占的百分比.
10.小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,可奶奶经营不善,经常有品种的牛奶滞销(没卖完)或脱销(量不够),造成了浪费或亏损,细心的小红结合所学的统计知识帮奶奶统计了一个星期牛奶的销售情况,并绘制了下表:
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高?
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定?
(3)假如你是小红,你会对奶奶有哪些好的建议.
第36课 概 率 初 步
1.两次投掷硬币,都是正面向上的概率是 .
2.“太阳每天从东方升起”这是一个 事件.(填“确定”或“不确定”)
3.有四张不透明的卡片为2, , ,除正面的数不同外,其余都相同,将它们背面朝上洗匀后,从中随机抽取一张卡片,抽到写有无理数卡片的概率 .
4.从两副拿掉大、小王的扑克牌中各抽取一张牌都是红桃的概率为 .
5.在一个不透明口袋中,装有若干个颜色不同,其余都相同的球,如果口袋中装4个红球且摸到红球的概率为,则口袋中球的总数是 .
6.图中的圆被六等分,他是可以自由转动的转盘,转动转盘,当转盘停止后,指针指向红色区域的概率 .
7.一个春光明媚的早晨,小明想去乡下姥姥家,享受美丽的“田园风光”,他匆匆来到就近的候车亭,这时他才知道10分钟一辆班车,2分钟内他能乘上班车的概率 .
8.飞蛾有较强的趋光性,夏夜一只可爱的小飞蛾想从玻璃窗外飞入,只有1m的窗户上有15cm15cm的一小块破洞,它能飞入的概率是 .
9.同时抛掷2枚一元的硬币,菊花图案都朝上的概率是( )
A. B. C. D.
10.从某班学生中随机选取一名学生是女生的概率为,则该班女生与男生的人数比是( )
A. B. C. D.
11.一个袋子里装有一双红色,一双绿色手套,两双手套除颜色不同外,其他完全相同,随机地从中摸出两只恰好是一双的概率( )
A. B. C. D.
12.在一个不透明的布袋中,红色,黑色,白色的玻璃球共有40个,除颜色外其他完全相同,小李通过多次模球试验后发现其中摸到红球,黑球的频率稳定在15%和45%,则口袋中白球的个数可能是 ( )
A.6 B.16 C.18 D.24
13.下列说法正确的是( )
A.一颗质地均匀的骰子连续投掷2000次,其中投掷5点的次数最少,则2001次一定投掷出5点;
B.某种彩票中奖率是1%,则买100张这种彩票一定会中奖;
C.天气预报说明明天下雨的概率是50%,所以明天将有一半时间下雨;
D.抛掷一枚图针,针尖触地和针尖朝上的概率不相等。
14.蚂蚁从甲地到乙地,共有三条路径,其中丙处有路障,则蚂蚁遇到路障的概率( )
A.1 B. C. D.0
15.田鼠喜欢歇身在土质松软的洞穴里,下图中空心洞穴为松土质洞穴,若田鼠从甲地出发,随机顺一条路寻找洞穴,求它一次就找到合适洞穴的概率。
16.如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可以使小灯泡发光。
(1)任意闭合其中一个开关,则小灯泡发光的概率是多少?
(2)任意闭合其中两个开关,请用画树状图或列表法求出小灯泡发光的概率。
17.某学校有A,B两个餐厅,甲,乙两名学生各自随机选择其中一个餐厅用餐:
⑴求甲、乙两名学生在同一餐厅用餐的概率;
⑵求甲、乙两名学生中至少有一名学生在B餐厅就餐的概率;
⑶如果餐厅数为A、B、C三个餐厅,甲、乙两名学生各自随机选择其中一个餐厅用餐,求甲、乙两名学生在同一餐厅用餐的概率;
(4)餐厅数为M个餐厅,N名学生各自随机选择其中一个餐厅用餐,求N名学生在同一餐厅用餐的概率。
18. 你喜欢玩游戏吗?小明、小刚、小军、小华四个小朋友一起玩掷骰子游戏,每只骰子都是一个正方体,每个面上有不同的点子数,点子数分别是1、2、3、4、5、6,一次投掷两枚,向上一面的点数和为2、6、10时小明胜,和为3、7、11时小刚胜,和为4、8、12时小军胜,和为1、5、9时小华胜。你认为这个游戏对四个小朋友公平吗?请你说明理由。
第六单元 统计与概率检测卷
(总分100分,时间60分钟)
一.选择题:(3分×9=27分)
1.国家统计局发布的统计公报显示:2001到2005年,我国GDP增长率分别为8.3%,9.1%,10.0%,10.1%,9.9%。经济学家评论说:这五年的年度GDP增长率之间相当平稳,从统计学的角度看, “增长率之间相当平稳”说明这组数据的( )比较小。
A.中位数 B.标准差 C.平均数 D.众数
2.某服装销售商在进行市场占有率的调查时,他最应该关注的是( )
A.服装型号的平均数 B.服装型号的众数
C.服装型号的中位数 D.最小的服装型号
3.图中甲、乙两户居民家庭全年支出费用的扇形统计图,根据统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
4.为了了解我市6000名学生参加的初中毕业会考 数学考试的成绩情况,从中抽取了200多考生的成绩进行统计,在这个问题中,下列说法:①这6000名学生的数学会考成绩的全体是总体;②每个考生是个体;③200名考生是总体的一个样本;④样本容量是200。其中说法正确的个数是( )
A.4个 B.3个 C.2个 D.1个
5.下列事件中确定事件是( )
A.掷一枚均匀的硬币,正面朝上
B.买一注福利彩票一定会中奖
C.把4个球放入三个抽屉中,其中一个抽屉中至少有2个球
D.掷一枚六个面分别标有1,2,3,4,5,6的骰子,骰子停止转动后奇数点朝上
6.在元旦游园晚会上有一个闯关活动:将5张背面完全一样正面分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关,那么一次过关的概率是( )
A. B. C. D.
7.有2名男生和2名女生,王老师要随机地、两两一对地为他们排座位,一男一女排在一起的概率是( )
A. B. C. D.
8.现有A、B两枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6)。用小莉掷A立方体朝上的数字为x,小明掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在已知抛物线y=-x2+4x上的概率为( )
A. B. C. D.
9.以下说法合理的是( )
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30%;
B.抛掷一枚普通正六面体骰子,出现6的概率是1/6的意思是每6次就有1次掷得6;
C.某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖;
D.在一次试验中,甲乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51.
二.填空题:(3分 ×10=30分)
10.把一组数据中的每一个数据都减去80,得一组新数据,若求得新一组数据的平均数是1.2,方差是4.4,则原来一组数据的平均数和方差分别为____________.
11.王老汉为了与客户签订购销合同,对自己的鱼塘中鱼的总重量进行估计,第一次捞出100条,称得重量为184kg,并将每条鱼作上记号放入水中;当它们完全混合于鱼群后,又捞出200条,称得重量为416kg,且带有记号的鱼有20条,王老汉的鱼塘中估计有鱼____________条,共重____________kg.
12.甲乙两人进行射击比赛,在相同条件下各射击10次,他们的平均成绩均为7环,10次射击成绩的方差分别是:S甲2=3,S乙2=1.2;成绩较为稳定的是____________.(填“甲”或“乙”)
13.从甲、乙、两三个厂家生产的同一种产品中,抽出8件产品,对其使用寿命进行跟踪调查,结果如下(单位:年)
甲:3,4,5,6,8,8,8,10
乙:4,6,6,6,8,9,12,13
丙:3,3,4,7,9,10,11,12
三个厂家的广告中都称该种产品的使用寿命是8,根据调查结果判断,厂家在广告中分别运用了平均数、众数、中位数中哪一种集中趋势的特征数;
甲:____________,乙:____________,丙:____________.
14.已知一组数据:-2,-2,3,-2,x,-1,若这组数据的平均数是0.5,则这组数据的中位数是____________.
15.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小张和小李两人中新手是____________.
第15题 第16题
16.如图所示,要把北京奥运的5个吉祥物“福娃”放在展桌上,有2个位置如图已定,其他3个“福娃”在各种不同位置放置的情况下,“迎迎”和“贝贝”的位置不相邻这一事件发生的概率为____________.
17.田忌赛马是一个为人熟知的故事,传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强。有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜,看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强。如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是____________.
18.抛掷两枚分别标有1,2,3,4的四面体骰子,写出这个实验中的一个可能事件是____________;写出这个实验中的一个必然事件是____________.
19.小明和小尹按如下规则做游戏:桌面上放有5支铅笔,每次取一支或两支,由小明先取,最后取完铅笔的人获胜。如果小明获胜的概率为1,那么小明第一次应该取走_________支.
三.解答题:(共43分)
20.(8分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员 工 管理人员 普通工作人员
人员结构 总经理 部门经理 科研人员 销售人员 高级技工 中级技工 勤杂工
员工数名 1 3 2 3 24 1
每人月工资/元 21000 8400 2025 2200 1800 1600 950
请你根据上述内容,解答下列问题:
⑴该公司“高级技工”有__________名;
⑵所有员工月工资的平均数x为2500元,中位数为_______元,众数为________元;
⑶去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保管整数),判断y能否反映该公司员工的月工资实际水平。
21.(8分)根据北京市统计局公布的2000年、2005年北京市人口数据,绘制统计图表如下:
2000年、2005年北京市常住人口中受教育程度情况统计表(人数单位:万人)
年份 大学程度人数(指大专及以上) 高中程度人数(含中专) 初中程度人数 小学程度人数 其他人数
2000年 233 320 475 234 120
2005年 362 372 476 212 114
请利用上述统计图表提供的信息回答下列问题:
⑴从2000年到2005年北京市常住人口增加了多少万人?
⑵2005年北京市常住人口中,少儿(0-14岁)人口约为多少万人?
⑶请结合2000年和2005年北京市常住人口受教育程度的状况,谈谈你的看法。
22.(9分)某报社为了解读者对本社一种报纸四个版面的喜欢情况,对读者作了一次问卷调查,要求读者选出自己最喜欢的一个版面,将所得数据整理后绘制成了如图的条形统计图;
⑴请写出从条形统计图中获得的一条信息;
⑵请根据条形统计图中的数据补全扇形统计图(要求:第二版与第三版相邻),并说明这两幅统计图各有什么特点?
⑶请你根据上述数据,对该报社提出一条合理的建议。
第22题 第23题
23.(9分)有一块表面是咖啡色、内部是白色、形状是正方体的烤面包。小明用刀在它的上表面、前表面和右侧表面沿虚线各切两刀,将它切成若干块小正方体形面包(如图)
⑴小明从若干块小面包中任取一块,求该块面包有且只有两个面是咖啡色的概率;
⑵小明和弟弟边吃边玩,游戏规则是:从中任取一块小面包,若它有奇数个面为咖啡色时,小明赢;否则,弟弟赢,你认为这样的游戏规则公平吧?为什么?如果不公平,请你修改游戏规则,使之公平。
24.(9分)小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,末掷入圈内不算,你来当裁判。
⑴你认为游戏公平吗?为什么?
⑵游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算非规则图形的面积呢?”。请你设计方案,解决这一问题。(要求画出图形,说明设计步骤、原理、写出公式)
三 统计与概率
第六单元 统计与概率
第34课 数据的收集、整理、描述答案:
1.不合理 2.5 3.⑴略 ⑵30% ⑶16~21 4.A 5.C 6.B 7.B
8.⑴50%;40%;8%;2% ⑵略 ⑶略 9.略
第35课 数据的分析答案
1.略 2.2.25 3.81.5分 4.略 5.82.3
6.C 7.A 8.D
9.(1)2,0.14,0.06,(2)1.05~1.55,(3)58%
10.(1)学生奶=3,酸牛奶=80,原味奶=40,金键酸牛奶销量高,
(2)12.57,91.71,96.86,金键学生奶销量最稳定,
(3)建议学生奶平常尽量少进或不进,周末可进几瓶.
第36课 概率初步答案
1. 2.确定 3. 4. 5.12 6. 7. 8.
9.C 10.A 11.A 12.B 13.D 14.C 15. 16. 、
17. 、、 、
18.不公平。小明为 ,小刚的概率为 , 小军为 ,小华的概率为
第六单元统计与概率检测卷 答案
一.选择题
1.B 2.B 3.D 4.C 5.C 6.D 7.D 8.B 9.D
二.填空题
10.81.2 , 4.4 11. 1000,2000 12.乙 13.众数, 平均数 ,中位数 14.
15.小李 16. 17. 18.朝上数字为2[答案不唯一] ,朝上数字≥1 19. 2
三.解答题
20.(1)16 (2)1700, 1600 (3)Y=(2500×50-21000-8400×3)÷46=1713
Y值是可以反映员工的月工资水平的
21.(1)1536-1382=154(万人)
(2)1382×10.2%=140.964(万人)
(3)大学程度人数比例逐渐提高(答案不唯一)
22.(1)参加调查人数为5000人(答案不唯一)(2)补图略,扇形图能清楚表示出喜欢各版面读者人数占所调查的总人数的百分比,条形图能清楚地表示出喜欢各版面的读者人数。(3)建议改进第二版的内容,提高文章质量。(答案不唯一)
23.(1) (2)1个面有8块,3个面有6块,所以小明赢的概为,弟弟赢的概为,所以不公平,应奇数面为咖啡色,小明得13分,反之,弟弟得14分。
24.(1)不公平,小红胜的机会为,小明胜的机会为。(2)设计一个矩形面积为s将不规则图形围起来,用石子随意向矩形中扔,扔在矩形中的次数m和不规则图中的次数n记下,如不规则图形面积为M,则M=s×()。画图略。
甲
乙
·丙
甲
D
A
B
C
同课章节目录
