24.4解直角三角形(3)
图片预览
文档简介
三案备课课时教案
河口初级中学 主备教师:数学组 二次备课教师:
课题 24.4解直角三角形(3) 课型 新授课 第 3课时
教学目标 知识与能力 理解坡角、坡度的概念,并能解直角三角形
过程与方法 通过综合运用直角三角形的相关知识解直角三角形,逐步培养学生分析问题解决问题的能力
情感态度与价值观 在教学中逐步培养学生分析问题、解决问题的能力,渗透数形结合的数学思想和方法
内容分析 教学重点 理解坡角、坡度的概念,并运用解直角三角形
教学难点 把实际问题转化为直角三角三角形求解
教法学法 启发诱导式 教具学具 三角板
教学过程 集体备课(共案) 二次备课修正(个案)年 月 日
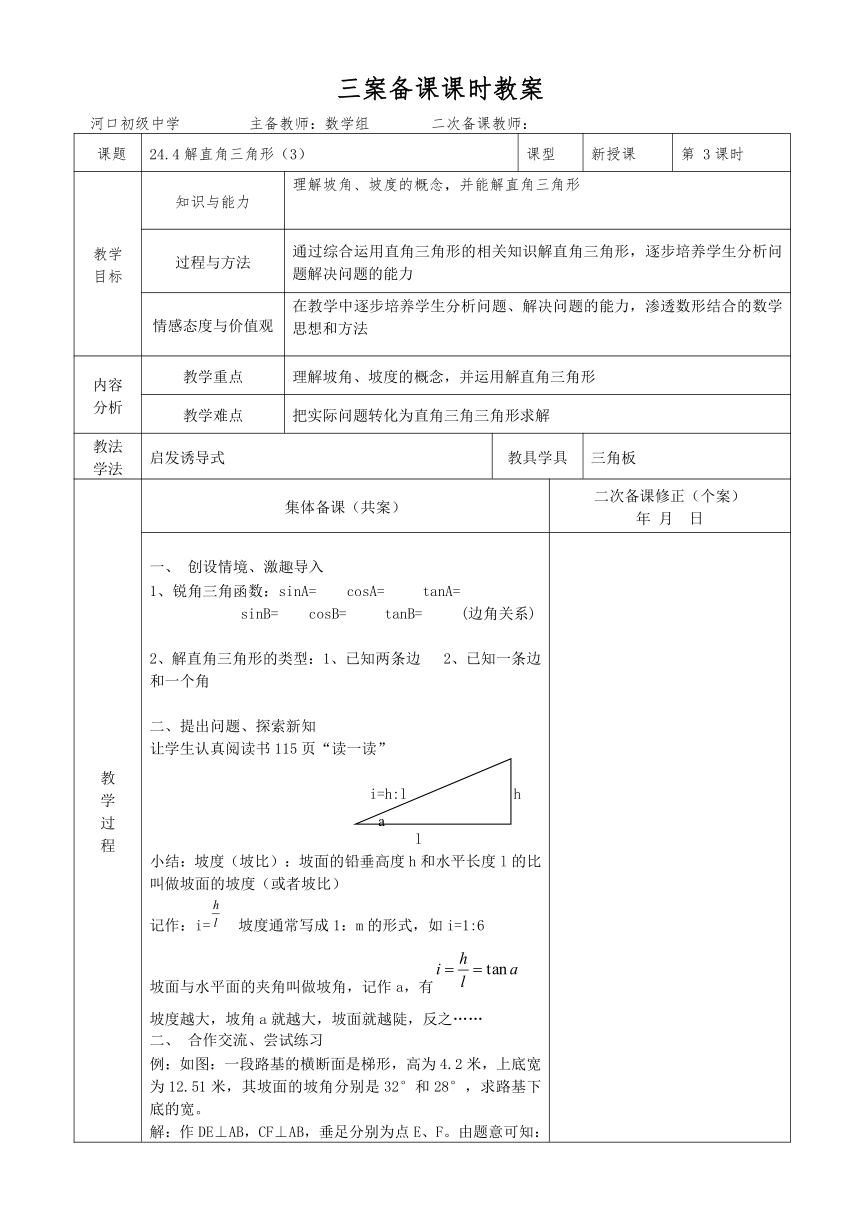
创设情境、激趣导入1、锐角三角函数:sinA= cosA= tanA= sinB= cosB= tanB= (边角关系)2、解直角三角形的类型:1、已知两条边 2、已知一条边和一个角二、提出问题、探索新知让学生认真阅读书115页“读一读” i=h:l h l小结:坡度(坡比):坡面的铅垂高度h和水平长度l的比叫做坡面的坡度(或者坡比)记作:i= 坡度通常写成1:m的形式,如i=1:6坡面与水平面的夹角叫做坡角,记作a,有坡度越大,坡角a就越大,坡面就越陡,反之……合作交流、尝试练习例:如图:一段路基的横断面是梯形,高为4.2米,上底宽为12.51米,其坡面的坡角分别是32°和28°,求路基下底的宽。解:作DE⊥AB,CF⊥AB,垂足分别为点E、F。由题意可知:DE=CF=4.2EF=CD=12.51在RT△ADE中, D C ( http: / / www.21cnjy.com ) A E F B 在RT△BCF中,同理可得∴AB=AE+EF+BF=6.72+12.51+7.90=27.1米答:路基下底的宽约为27.1米联系实际、应用拓展如图:水库大坝的横断面是梯形,坝顶宽6米 ( http: / / www.21cnjy.com ),坝高23米,斜坡AB的坡度i=1:3,斜坡CD的坡度i=1:2.5,求斜坡AB的坡面角a,坝底宽AD和斜坡AB的长。 B C A B解:(略)归纳小结、巩固练习1、读一读:书116“读一读”利用解直角三角形的知识解决实际问题的一般过程是:2、练习116EX1 ,117页4题
板书 24.4解直角三角形(3)引入: 坡角、坡度: 例 利用解直角三角形的知识解决实际问题的一般过程是:
作业设计 书117页2题练习册71-72页
教后反思
字体仿宋,5号
a
河口初级中学 主备教师:数学组 二次备课教师:
课题 24.4解直角三角形(3) 课型 新授课 第 3课时
教学目标 知识与能力 理解坡角、坡度的概念,并能解直角三角形
过程与方法 通过综合运用直角三角形的相关知识解直角三角形,逐步培养学生分析问题解决问题的能力
情感态度与价值观 在教学中逐步培养学生分析问题、解决问题的能力,渗透数形结合的数学思想和方法
内容分析 教学重点 理解坡角、坡度的概念,并运用解直角三角形
教学难点 把实际问题转化为直角三角三角形求解
教法学法 启发诱导式 教具学具 三角板
教学过程 集体备课(共案) 二次备课修正(个案)年 月 日
创设情境、激趣导入1、锐角三角函数:sinA= cosA= tanA= sinB= cosB= tanB= (边角关系)2、解直角三角形的类型:1、已知两条边 2、已知一条边和一个角二、提出问题、探索新知让学生认真阅读书115页“读一读” i=h:l h l小结:坡度(坡比):坡面的铅垂高度h和水平长度l的比叫做坡面的坡度(或者坡比)记作:i= 坡度通常写成1:m的形式,如i=1:6坡面与水平面的夹角叫做坡角,记作a,有坡度越大,坡角a就越大,坡面就越陡,反之……合作交流、尝试练习例:如图:一段路基的横断面是梯形,高为4.2米,上底宽为12.51米,其坡面的坡角分别是32°和28°,求路基下底的宽。解:作DE⊥AB,CF⊥AB,垂足分别为点E、F。由题意可知:DE=CF=4.2EF=CD=12.51在RT△ADE中, D C ( http: / / www.21cnjy.com ) A E F B 在RT△BCF中,同理可得∴AB=AE+EF+BF=6.72+12.51+7.90=27.1米答:路基下底的宽约为27.1米联系实际、应用拓展如图:水库大坝的横断面是梯形,坝顶宽6米 ( http: / / www.21cnjy.com ),坝高23米,斜坡AB的坡度i=1:3,斜坡CD的坡度i=1:2.5,求斜坡AB的坡面角a,坝底宽AD和斜坡AB的长。 B C A B解:(略)归纳小结、巩固练习1、读一读:书116“读一读”利用解直角三角形的知识解决实际问题的一般过程是:2、练习116EX1 ,117页4题
板书 24.4解直角三角形(3)引入: 坡角、坡度: 例 利用解直角三角形的知识解决实际问题的一般过程是:
作业设计 书117页2题练习册71-72页
教后反思
字体仿宋,5号
a
