华师大版数学八年级上册 13.2.1 全等三角形 教案
文档属性
| 名称 | 华师大版数学八年级上册 13.2.1 全等三角形 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 14:24:38 | ||
图片预览

文档简介
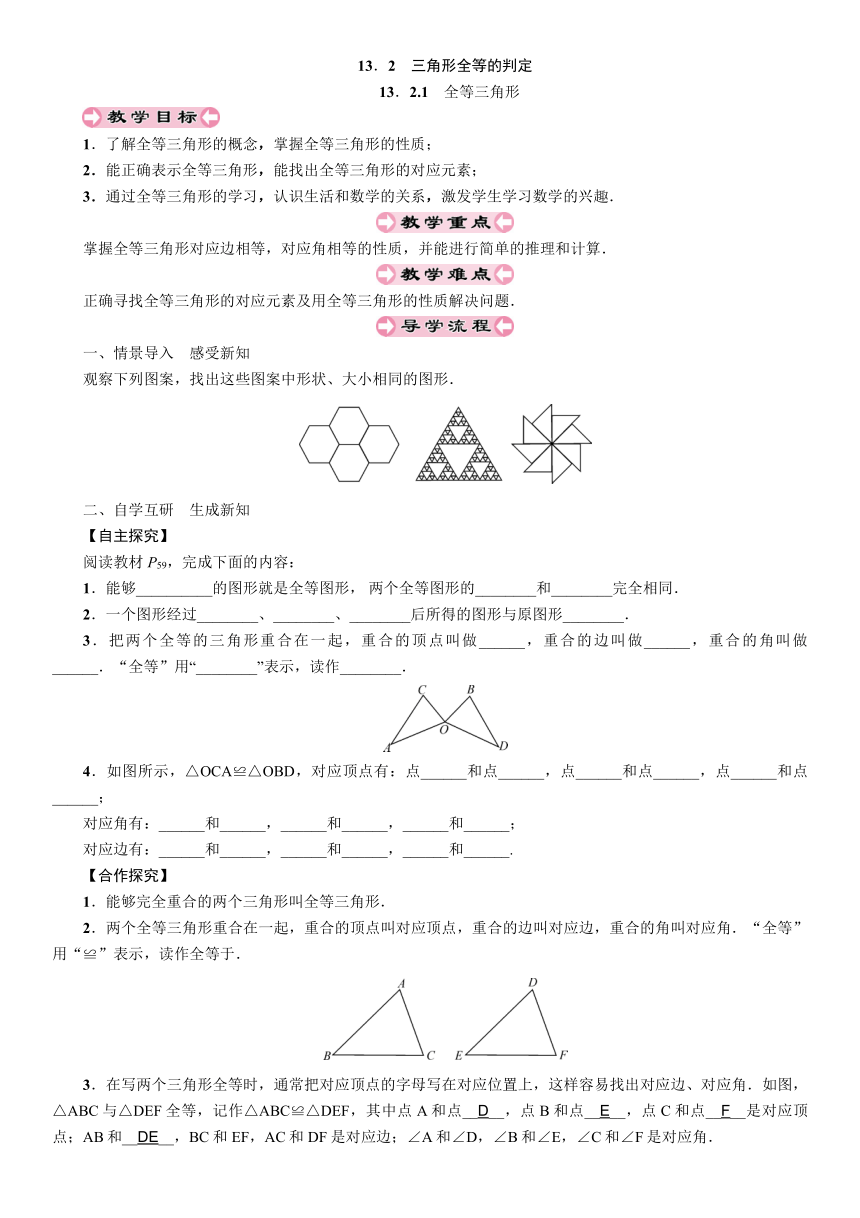
13.2 三角形全等的判定
13.2.1 全等三角形
1.了解全等三角形的概念,掌握全等三角形的性质;
2.能正确表示全等三角形,能找出全等三角形的对应元素;
3.通过全等三角形的学习,认识生活和数学的关系,激发学生学习数学的兴趣.
掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算.
正确寻找全等三角形的对应元素及用全等三角形的性质解决问题.
一、情景导入 感受新知
观察下列图案,找出这些图案中形状、大小相同的图形.
二、自学互研 生成新知
【自主探究】
阅读教材P59,完成下面的内容:
1.能够__________的图形就是全等图形, 两个全等图形的________和________完全相同.
2.一个图形经过________、________、________后所得的图形与原图形________.
3.把两个全等的三角形重合在一起,重合的顶点叫做______,重合的边叫做______,重合的角叫做______.“全等”用“________”表示,读作________.
4.如图所示,△OCA≌△OBD,对应顶点有:点______和点______,点______和点______,点______和点______;
对应角有:______和______,______和______,______和______;
对应边有:______和______,______和______,______和______.
【合作探究】
1.能够完全重合的两个三角形叫全等三角形.
2.两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.“全等”用“≌”表示,读作全等于.
3.在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点__D__,点B和点__E__,点C和点__F__是对应顶点;AB和__DE__,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
4.全等三角形的对应边相等;全等三角形的对应角相等.
【师生活动】①明了学情:关注学生对全等概念和性质的理解和掌握情况.
②差异指导:对学生在探究过程中产生的疑惑及时引导与点拨.
③生生互助:学生在小组内交流、讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
例:如图△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.
在△NMH中,MH是最长边.EF=2.1cm,EH=1.1cm,HN=3.3cm.
(1)写出其他对应边及对应角.
(2)求线段MN及线段HG的长.
(学生合作完成)
四、课堂小结 回顾新知
通过本节课学习,你有了哪些新的收获?还有哪些疑惑?请谈一谈你的想法和同学们一起分享.
五、检测反馈 落实新知
1.如图所示,若△OAD≌△OBC,∠O=65°,∠C=20°,则∠OAD=__95°__.
,(第2题图))
2.如图,若△ABC≌△DEF,回答下列问题:
(1)若△ABC的周长为17cm,BC=6cm,DE=5cm,则DF=__6__cm;
(2)若∠A =50°,∠E=75°,则∠B=__75°__.
3.如图,△AOB≌△COD,那么∠ABD与∠CDB相等吗?为什么?
解:相等.∵△AOB≌△COD,
∴OB=OD,∠ABO=∠CDO.
∵OB=OD,∠OBD=∠ODB,
即:∠ABD=∠CDB.
,(第3题图)) ,(第4题图))
4.如图:Rt△ABC中,∠ A=90°,若△ADB≌△EDB≌△EDC,则∠C=__30°__.
5.如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,求∠BAC的度数.
解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠CAE=∠BAD=40°,
∴∠BAC=∠BAE-∠CAE=120°-40°=80°,即∠BAC=80°
六、课后作业 巩固新知
见学生用书.
13.2.1 全等三角形
1.了解全等三角形的概念,掌握全等三角形的性质;
2.能正确表示全等三角形,能找出全等三角形的对应元素;
3.通过全等三角形的学习,认识生活和数学的关系,激发学生学习数学的兴趣.
掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算.
正确寻找全等三角形的对应元素及用全等三角形的性质解决问题.
一、情景导入 感受新知
观察下列图案,找出这些图案中形状、大小相同的图形.
二、自学互研 生成新知
【自主探究】
阅读教材P59,完成下面的内容:
1.能够__________的图形就是全等图形, 两个全等图形的________和________完全相同.
2.一个图形经过________、________、________后所得的图形与原图形________.
3.把两个全等的三角形重合在一起,重合的顶点叫做______,重合的边叫做______,重合的角叫做______.“全等”用“________”表示,读作________.
4.如图所示,△OCA≌△OBD,对应顶点有:点______和点______,点______和点______,点______和点______;
对应角有:______和______,______和______,______和______;
对应边有:______和______,______和______,______和______.
【合作探究】
1.能够完全重合的两个三角形叫全等三角形.
2.两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.“全等”用“≌”表示,读作全等于.
3.在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点__D__,点B和点__E__,点C和点__F__是对应顶点;AB和__DE__,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.
4.全等三角形的对应边相等;全等三角形的对应角相等.
【师生活动】①明了学情:关注学生对全等概念和性质的理解和掌握情况.
②差异指导:对学生在探究过程中产生的疑惑及时引导与点拨.
③生生互助:学生在小组内交流、讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
例:如图△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.
在△NMH中,MH是最长边.EF=2.1cm,EH=1.1cm,HN=3.3cm.
(1)写出其他对应边及对应角.
(2)求线段MN及线段HG的长.
(学生合作完成)
四、课堂小结 回顾新知
通过本节课学习,你有了哪些新的收获?还有哪些疑惑?请谈一谈你的想法和同学们一起分享.
五、检测反馈 落实新知
1.如图所示,若△OAD≌△OBC,∠O=65°,∠C=20°,则∠OAD=__95°__.
,(第2题图))
2.如图,若△ABC≌△DEF,回答下列问题:
(1)若△ABC的周长为17cm,BC=6cm,DE=5cm,则DF=__6__cm;
(2)若∠A =50°,∠E=75°,则∠B=__75°__.
3.如图,△AOB≌△COD,那么∠ABD与∠CDB相等吗?为什么?
解:相等.∵△AOB≌△COD,
∴OB=OD,∠ABO=∠CDO.
∵OB=OD,∠OBD=∠ODB,
即:∠ABD=∠CDB.
,(第3题图)) ,(第4题图))
4.如图:Rt△ABC中,∠ A=90°,若△ADB≌△EDB≌△EDC,则∠C=__30°__.
5.如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,求∠BAC的度数.
解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠CAE=∠BAD=40°,
∴∠BAC=∠BAE-∠CAE=120°-40°=80°,即∠BAC=80°
六、课后作业 巩固新知
见学生用书.
