华师大版数学八年级上册 13.5.3 角平分线教案
文档属性
| 名称 | 华师大版数学八年级上册 13.5.3 角平分线教案 | 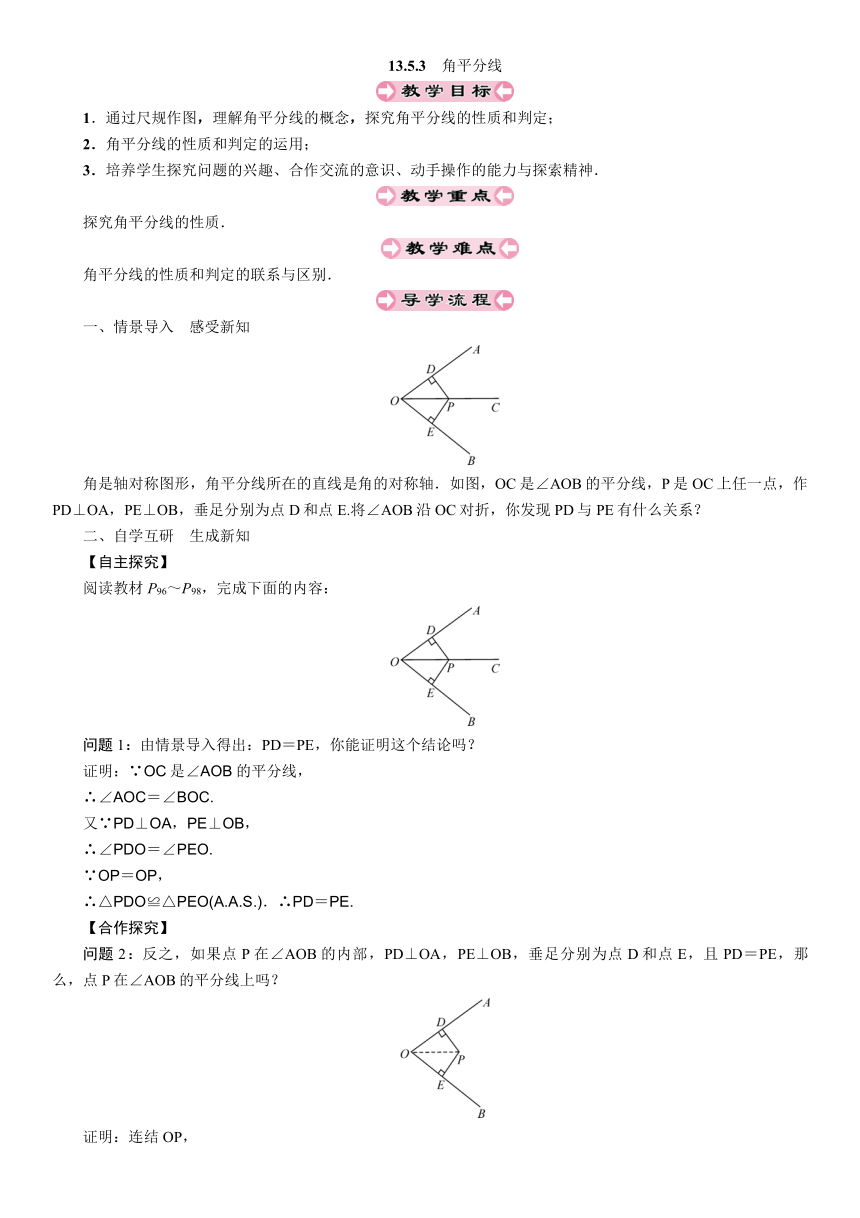 | |
| 格式 | doc | ||
| 文件大小 | 125.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 14:24:45 | ||
图片预览

文档简介
13.5.3 角平分线
1.通过尺规作图,理解角平分线的概念,探究角平分线的性质和判定;
2.角平分线的性质和判定的运用;
3.培养学生探究问题的兴趣、合作交流的意识、动手操作的能力与探索精神.
探究角平分线的性质.
角平分线的性质和判定的联系与区别.
一、情景导入 感受新知
角是轴对称图形,角平分线所在的直线是角的对称轴.如图,OC是∠AOB的平分线,P是OC上任一点,作PD⊥OA,PE⊥OB,垂足分别为点D和点E.将∠AOB沿OC对折,你发现PD与PE有什么关系?
二、自学互研 生成新知
【自主探究】
阅读教材P96~P98,完成下面的内容:
问题1:由情景导入得出:PD=PE,你能证明这个结论吗?
证明:∵OC是∠AOB的平分线,
∴∠AOC=∠BOC.
又∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO.
∵OP=OP,
∴△PDO≌△PEO(A.A.S.).∴PD=PE.
【合作探究】
问题2:反之,如果点P在∠AOB的内部,PD⊥OA,PE⊥OB,垂足分别为点D和点E,且PD=PE,那么,点P在∠AOB的平分线上吗?
证明:连结OP,
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
又∵OP=OP,PD=PE,
∴△PDO≌△PEO(H.L.).
∴∠AOP=∠BOP.
∴OP平分∠AOB.
∴点P在∠AOB的平分线上.
归纳:(1)角平分线的性质定理:角平分线上的点到角两边的距离相等.
(2)角平分线的判定定理:角的内部到角两边距离相等的点在角的平分线上.
【师生活动】①明了学情:关注学生对角的平分线性质和判定的理解和掌握情况.
②差异指导:对学生在探究过程中产生的疑惑及时引导与点拨.
③生生互助:学生在小组内交流、讨论,相互释疑,达成共识
三、典例剖析 运用新知
【合作探究】
例1:如图,在△ABC中,∠C=90°,AD为∠BAC的平分线,△ABC的面积是28cm2,AB=16cm,AC=12cm,求CD的长.
解:过点D作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,∠C=90°即AC⊥CD,
∴DE=CD.
∵S△ABC=S△ACD+S△ABD=AC×CD+AB×DE=28,
∴×12CD+×16CD=28.
∴CD=2cm.
例2:已知:如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于E,DF⊥AC于F,且DB=DC.试证明:BE=CF.
证明:∵AD是∠BAC的平分线,
DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°.
又∵DB=DC,∴△DEB≌△DFC(H.L.).
∴BE=CF.
四、课堂小结 回顾新知
通过本节课学习,你有了哪些新的收获?还有哪些疑惑?请谈一谈你的想法和同学们一起分享.
五、检测反馈 落实新知
1.如图所示,AD平分∠BAC,DE⊥AB,垂足为E,DF⊥AC,垂足为F,则下列结论不正确的是(D)
A.△AEG≌△AFG B.△AED≌△AFD
C.△DEG≌△DFG D.△BDE≌△CDF
2.∠AOB的平分线上一点M,M到OA的距离为2cm,则M到OB的距离为__2cm__.
3.在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,若BC=16,BD=10,则D到AB的距离是__6__.
4.如图在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离
相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试.
解:提示,AB垂直平分线与L1与L2构成的角的角平分线的交点。
六、课后作业 巩固新知
见学生用书.
1.通过尺规作图,理解角平分线的概念,探究角平分线的性质和判定;
2.角平分线的性质和判定的运用;
3.培养学生探究问题的兴趣、合作交流的意识、动手操作的能力与探索精神.
探究角平分线的性质.
角平分线的性质和判定的联系与区别.
一、情景导入 感受新知
角是轴对称图形,角平分线所在的直线是角的对称轴.如图,OC是∠AOB的平分线,P是OC上任一点,作PD⊥OA,PE⊥OB,垂足分别为点D和点E.将∠AOB沿OC对折,你发现PD与PE有什么关系?
二、自学互研 生成新知
【自主探究】
阅读教材P96~P98,完成下面的内容:
问题1:由情景导入得出:PD=PE,你能证明这个结论吗?
证明:∵OC是∠AOB的平分线,
∴∠AOC=∠BOC.
又∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO.
∵OP=OP,
∴△PDO≌△PEO(A.A.S.).∴PD=PE.
【合作探究】
问题2:反之,如果点P在∠AOB的内部,PD⊥OA,PE⊥OB,垂足分别为点D和点E,且PD=PE,那么,点P在∠AOB的平分线上吗?
证明:连结OP,
∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
又∵OP=OP,PD=PE,
∴△PDO≌△PEO(H.L.).
∴∠AOP=∠BOP.
∴OP平分∠AOB.
∴点P在∠AOB的平分线上.
归纳:(1)角平分线的性质定理:角平分线上的点到角两边的距离相等.
(2)角平分线的判定定理:角的内部到角两边距离相等的点在角的平分线上.
【师生活动】①明了学情:关注学生对角的平分线性质和判定的理解和掌握情况.
②差异指导:对学生在探究过程中产生的疑惑及时引导与点拨.
③生生互助:学生在小组内交流、讨论,相互释疑,达成共识
三、典例剖析 运用新知
【合作探究】
例1:如图,在△ABC中,∠C=90°,AD为∠BAC的平分线,△ABC的面积是28cm2,AB=16cm,AC=12cm,求CD的长.
解:过点D作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,∠C=90°即AC⊥CD,
∴DE=CD.
∵S△ABC=S△ACD+S△ABD=AC×CD+AB×DE=28,
∴×12CD+×16CD=28.
∴CD=2cm.
例2:已知:如图,AD是∠BAC的平分线,DE⊥AB,交AB的延长线于E,DF⊥AC于F,且DB=DC.试证明:BE=CF.
证明:∵AD是∠BAC的平分线,
DE⊥AB,DF⊥AC,
∴DE=DF,∠DEB=∠DFC=90°.
又∵DB=DC,∴△DEB≌△DFC(H.L.).
∴BE=CF.
四、课堂小结 回顾新知
通过本节课学习,你有了哪些新的收获?还有哪些疑惑?请谈一谈你的想法和同学们一起分享.
五、检测反馈 落实新知
1.如图所示,AD平分∠BAC,DE⊥AB,垂足为E,DF⊥AC,垂足为F,则下列结论不正确的是(D)
A.△AEG≌△AFG B.△AED≌△AFD
C.△DEG≌△DFG D.△BDE≌△CDF
2.∠AOB的平分线上一点M,M到OA的距离为2cm,则M到OB的距离为__2cm__.
3.在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,若BC=16,BD=10,则D到AB的距离是__6__.
4.如图在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离
相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试.
解:提示,AB垂直平分线与L1与L2构成的角的角平分线的交点。
六、课后作业 巩固新知
见学生用书.
