12.2全等三角形的判定和应用 同步练习题(含答案)
文档属性
| 名称 | 12.2全等三角形的判定和应用 同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 10:25:27 | ||
图片预览

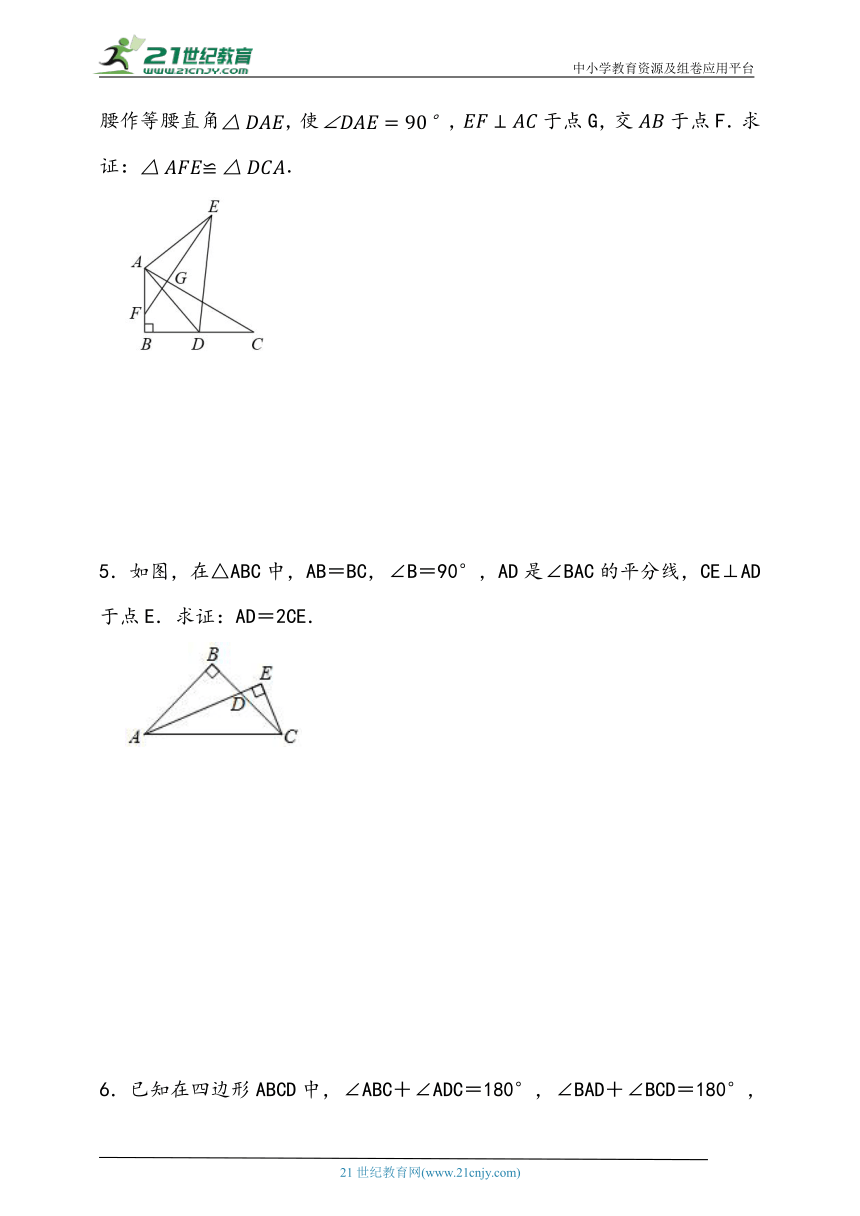

文档简介
中小学教育资源及组卷应用平台
12.2全等三角形的判定和应用 人教版数学 八年级上册
一、三角形全等的判定
1.下列结论:
①周长相等的两个等边三角形全等;
②周长相等的两个等腰三角形全等;
③面积相等的两个等边三角形全等;
④面积相等的两个等腰三角形全等;
其中所有正确结论的序号是 .
2.如图,是等腰三角形,点,分别在腰,上,且,,连接,交于点.则:
(1)图中有 对全等三角形;
(2)若点恰好为的中点,且的面积为2,则四边形的面积为 .
3.作图题:在如图所示的 方格中,每个小方格都是边长为1的正方形, 是格点三角形(即顶点恰好是正方形的顶点),请做出与 有一条公共边且全等的所有格点三角形.
4.如图,在中,,点D是线段上一点,以为腰作等腰直角,使,于点G,交于点F.求证:.
5.如图,在△ABC中,AB=BC,∠B=90°,AD是∠BAC的平分线,CE⊥AD于点E.求证:AD=2CE.
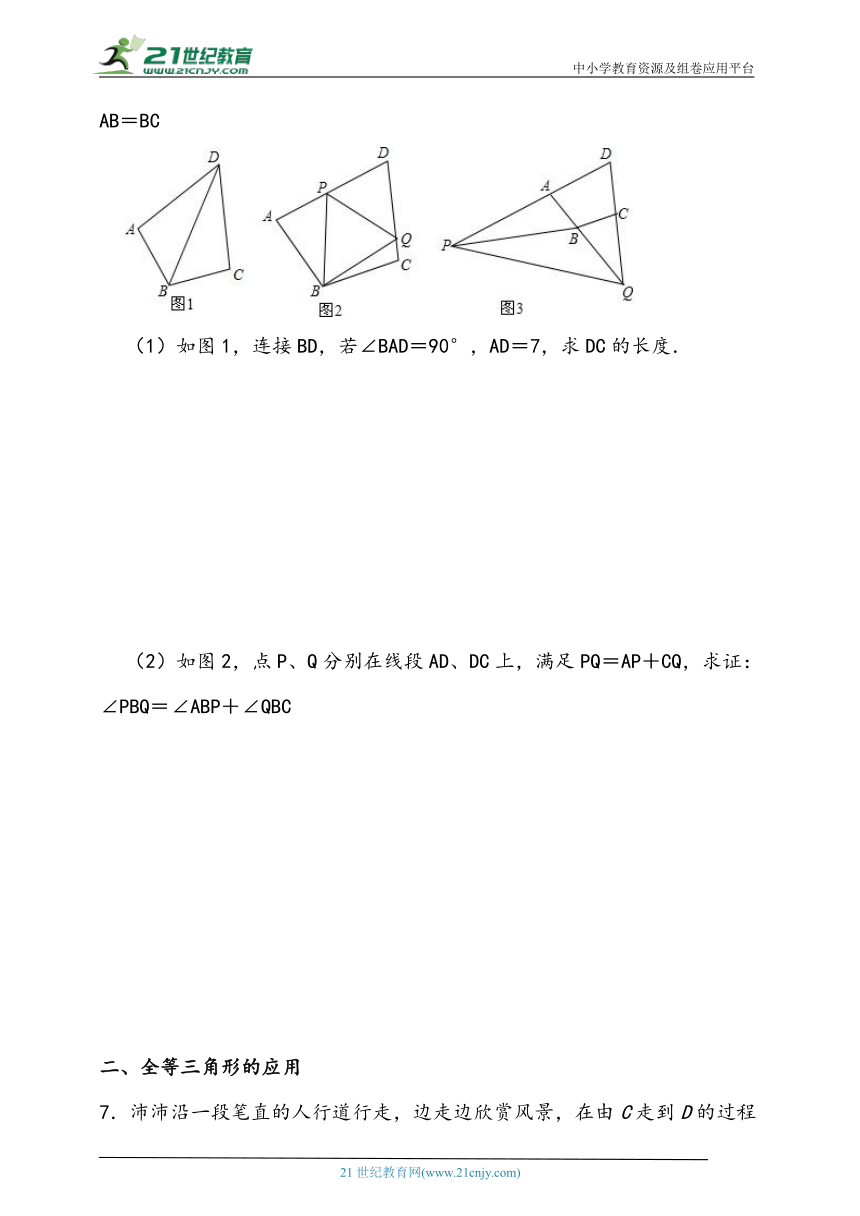
6.已知在四边形ABCD中,∠ABC+∠ADC=180°,∠BAD+∠BCD=180°,AB=BC
(1)如图1,连接BD,若∠BAD=90°,AD=7,求DC的长度.
(2)如图2,点P、Q分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=∠ABP+∠QBC
二、全等三角形的应用
7.沛沛沿一段笔直的人行道行走,边走边欣赏风景,在由C走到D的过程中,通过隔离带的空隙P,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图,////,相邻两平行线间的距离相等,AC,BD相交于P,垂足为D.已知米.请根据上述信息求标语AB的长度 .
8.在新年联欢会上,老师设计了“你说我画”的游戏.游戏规则如下:甲同学需要根据乙同学提供的三个条件画出形状和大小都确定的三角形.已知乙同学说出的前两个条件是“,”.现仅存下列三个条件:①;②;③.为了甲同学画出形状和大小都确定的,乙同学可以选择的条件有: .(填写序号,写出所有正确答案)
9.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小敏从水平位置CD下降40cm时,这时小明离地面的高度是 .
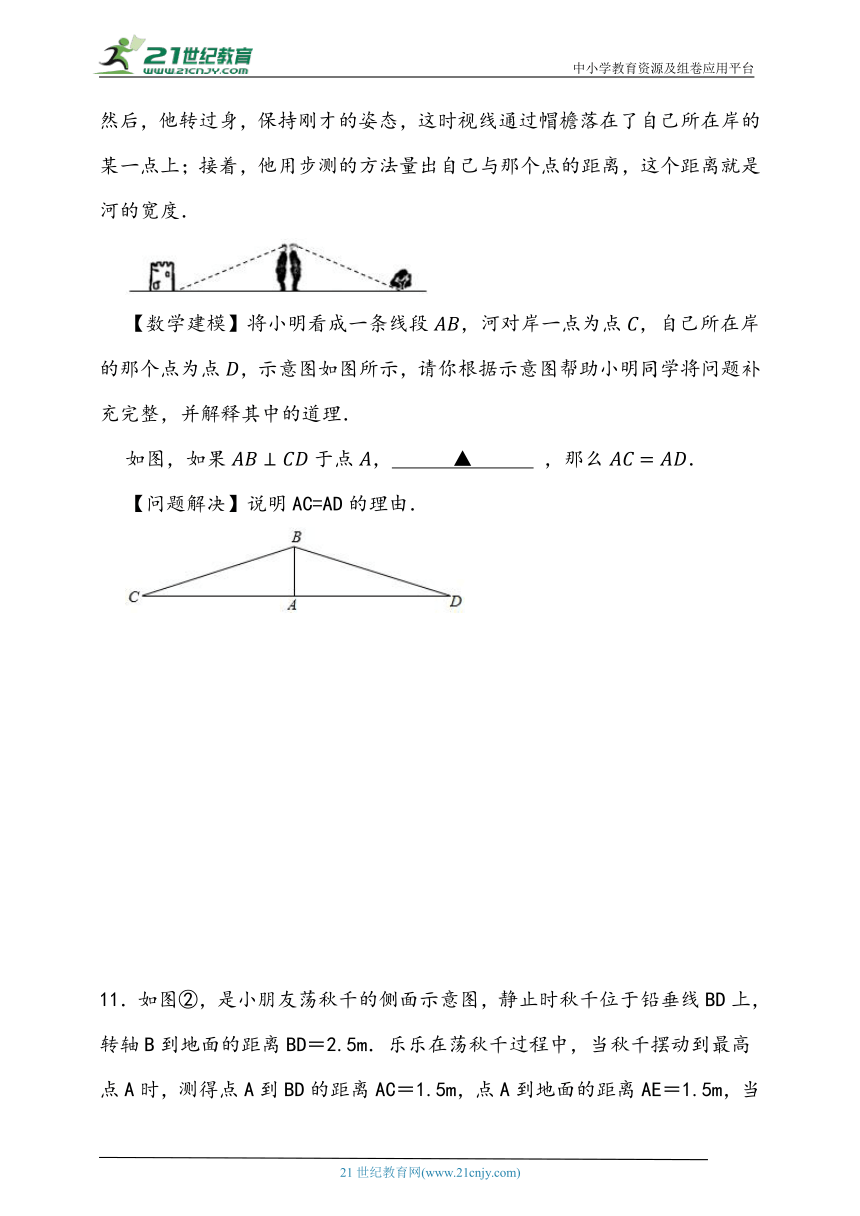
10.【实际问题】在拓展训练过程中,小明和组员为了完成测河宽的任务,在不能过河测量又没有任何测量工具的情况下,设计出下面的方案:小明面向河对岸的方向站好,然后调整帽子,使视线通过帽檐正好落在河对岸一点;然后,他转过身,保持刚才的姿态,这时视线通过帽檐落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是河的宽度.
【数学建模】将小明看成一条线段,河对岸一点为点,自己所在岸的那个点为点,示意图如图所示,请你根据示意图帮助小明同学将问题补充完整,并解释其中的道理.
如图,如果于点, ▲ ,那么.
【问题解决】说明AC=AD的理由.
11.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
12.课间,小刚拿着老师的等腰直角三角板玩,一不小心掉到垂直地面的两个木块之间,如图所示:
(1)求证:△ADC≌△CEB;
(2)若测得AD=15cm,BE=10cm,求两个木块之间的距离DE的长.
答案解析部分
1.【答案】①③
2.【答案】(1)3
(2)6
3.【答案】解:如图所示:
以BC为边的三角形有3个,分别是△A1BC、△A2BC、△A3BC,以AC为公共边的三角形有1个,是△AB1C,以AB为边的三角形不存在.
综上,共有4个与 有一条公共边且全等的三角形.
4.【答案】证明:∵,
∴,
∵,即,
∴,,
∴,
∵,
∴,
∴,
∵,
∴.
5.【答案】证明:延长AB、CE交于点F,
∵∠ABC=90°,CE⊥AD,∠ADB=∠CDE,
∴∠BAD=∠ECD,
在△ABD和△CBF中,
,
∴△ABD≌△CBF(SAS),
∴AD=CF,
∵AD是∠BAC的平分线,
∴∠CAE=∠FAE,
在△CAE和△FAE中,
,
∴△CAE≌△FAE(ASA),
∴CE=EF,
∴AD=CF=2CE.
6.【答案】(1)证明:如图1,
∵,,
∴,
在和中,
∴,
∴,
∴;
(2)证明:如图2,
延长至点,使得,连接
∵,
∴,
∵,
∴,
∵,,
∴,
∴,,
∵,,
∴,
∵,,
∴,
∴,
∴;
7.【答案】16
8.【答案】②
9.【答案】90cm
10.【答案】解:;
理由如下:,
,
在与中,
,
≌,
.
11.【答案】解:作A′F⊥BD,垂足为F,如图:
设∠A′BF=∠1,∠BA′F=∠3,∠ABF=∠2,
∵AC⊥BD,
∴∠ACB=∠A′FB,
在Rt△A′FB中,∠1+∠3=90°,
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3,
∴在△ACB和△BFA′中,
∴△ACB≌△BFA′(AAS),
∴A′F=BC,
∵AC//DE且CD⊥AC,AE⊥DE,
∴CD=AE=1.5m,
∴BC=BD-CD=2.5-1.5=1m
即A′F=1m
即A'到BD的距离为1m.
12.【答案】(1)由题意,得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,∠ACD+∠BCE=90°.
∴∠ACD+∠CAD=90°.
∴∠CAD=∠BCE,
又∵AC=CB,
∴△ADC≌△CEB(AAS);
(2)∵△ADC≌△CEB,
∴CD=BE,AD=CE,
∵DE=CD+CE,
∴DE=BE+AD=10+15=25(cm).
∴两墙之间的距离DE的长为25cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
12.2全等三角形的判定和应用 人教版数学 八年级上册
一、三角形全等的判定
1.下列结论:
①周长相等的两个等边三角形全等;
②周长相等的两个等腰三角形全等;
③面积相等的两个等边三角形全等;
④面积相等的两个等腰三角形全等;
其中所有正确结论的序号是 .
2.如图,是等腰三角形,点,分别在腰,上,且,,连接,交于点.则:
(1)图中有 对全等三角形;
(2)若点恰好为的中点,且的面积为2,则四边形的面积为 .
3.作图题:在如图所示的 方格中,每个小方格都是边长为1的正方形, 是格点三角形(即顶点恰好是正方形的顶点),请做出与 有一条公共边且全等的所有格点三角形.
4.如图,在中,,点D是线段上一点,以为腰作等腰直角,使,于点G,交于点F.求证:.
5.如图,在△ABC中,AB=BC,∠B=90°,AD是∠BAC的平分线,CE⊥AD于点E.求证:AD=2CE.
6.已知在四边形ABCD中,∠ABC+∠ADC=180°,∠BAD+∠BCD=180°,AB=BC
(1)如图1,连接BD,若∠BAD=90°,AD=7,求DC的长度.
(2)如图2,点P、Q分别在线段AD、DC上,满足PQ=AP+CQ,求证:∠PBQ=∠ABP+∠QBC
二、全等三角形的应用
7.沛沛沿一段笔直的人行道行走,边走边欣赏风景,在由C走到D的过程中,通过隔离带的空隙P,刚好浏览完对面人行道宣传墙上的一条标语,具体信息如下:如图,////,相邻两平行线间的距离相等,AC,BD相交于P,垂足为D.已知米.请根据上述信息求标语AB的长度 .
8.在新年联欢会上,老师设计了“你说我画”的游戏.游戏规则如下:甲同学需要根据乙同学提供的三个条件画出形状和大小都确定的三角形.已知乙同学说出的前两个条件是“,”.现仅存下列三个条件:①;②;③.为了甲同学画出形状和大小都确定的,乙同学可以选择的条件有: .(填写序号,写出所有正确答案)
9.如图,小明与小敏玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小敏从水平位置CD下降40cm时,这时小明离地面的高度是 .
10.【实际问题】在拓展训练过程中,小明和组员为了完成测河宽的任务,在不能过河测量又没有任何测量工具的情况下,设计出下面的方案:小明面向河对岸的方向站好,然后调整帽子,使视线通过帽檐正好落在河对岸一点;然后,他转过身,保持刚才的姿态,这时视线通过帽檐落在了自己所在岸的某一点上;接着,他用步测的方法量出自己与那个点的距离,这个距离就是河的宽度.
【数学建模】将小明看成一条线段,河对岸一点为点,自己所在岸的那个点为点,示意图如图所示,请你根据示意图帮助小明同学将问题补充完整,并解释其中的道理.
如图,如果于点, ▲ ,那么.
【问题解决】说明AC=AD的理由.
11.如图②,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=2.5m.乐乐在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=1.5m,点A到地面的距离AE=1.5m,当他从A处摆动到A'处时,若A'B⊥AB,求A'到BD的距离.
12.课间,小刚拿着老师的等腰直角三角板玩,一不小心掉到垂直地面的两个木块之间,如图所示:
(1)求证:△ADC≌△CEB;
(2)若测得AD=15cm,BE=10cm,求两个木块之间的距离DE的长.
答案解析部分
1.【答案】①③
2.【答案】(1)3
(2)6
3.【答案】解:如图所示:
以BC为边的三角形有3个,分别是△A1BC、△A2BC、△A3BC,以AC为公共边的三角形有1个,是△AB1C,以AB为边的三角形不存在.
综上,共有4个与 有一条公共边且全等的三角形.
4.【答案】证明:∵,
∴,
∵,即,
∴,,
∴,
∵,
∴,
∴,
∵,
∴.
5.【答案】证明:延长AB、CE交于点F,
∵∠ABC=90°,CE⊥AD,∠ADB=∠CDE,
∴∠BAD=∠ECD,
在△ABD和△CBF中,
,
∴△ABD≌△CBF(SAS),
∴AD=CF,
∵AD是∠BAC的平分线,
∴∠CAE=∠FAE,
在△CAE和△FAE中,
,
∴△CAE≌△FAE(ASA),
∴CE=EF,
∴AD=CF=2CE.
6.【答案】(1)证明:如图1,
∵,,
∴,
在和中,
∴,
∴,
∴;
(2)证明:如图2,
延长至点,使得,连接
∵,
∴,
∵,
∴,
∵,,
∴,
∴,,
∵,,
∴,
∵,,
∴,
∴,
∴;
7.【答案】16
8.【答案】②
9.【答案】90cm
10.【答案】解:;
理由如下:,
,
在与中,
,
≌,
.
11.【答案】解:作A′F⊥BD,垂足为F,如图:
设∠A′BF=∠1,∠BA′F=∠3,∠ABF=∠2,
∵AC⊥BD,
∴∠ACB=∠A′FB,
在Rt△A′FB中,∠1+∠3=90°,
又∵A'B⊥AB,
∴∠1+∠2=90°,
∴∠2=∠3,
∴在△ACB和△BFA′中,
∴△ACB≌△BFA′(AAS),
∴A′F=BC,
∵AC//DE且CD⊥AC,AE⊥DE,
∴CD=AE=1.5m,
∴BC=BD-CD=2.5-1.5=1m
即A′F=1m
即A'到BD的距离为1m.
12.【答案】(1)由题意,得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,∠ACD+∠BCE=90°.
∴∠ACD+∠CAD=90°.
∴∠CAD=∠BCE,
又∵AC=CB,
∴△ADC≌△CEB(AAS);
(2)∵△ADC≌△CEB,
∴CD=BE,AD=CE,
∵DE=CD+CE,
∴DE=BE+AD=10+15=25(cm).
∴两墙之间的距离DE的长为25cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
