北师大版数学八年级上册 4.1 函数 课件(共46张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 4.1 函数 课件(共46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-17 20:34:35 | ||
图片预览








文档简介
(共46张PPT)
第四章 一次函数
1 函数
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
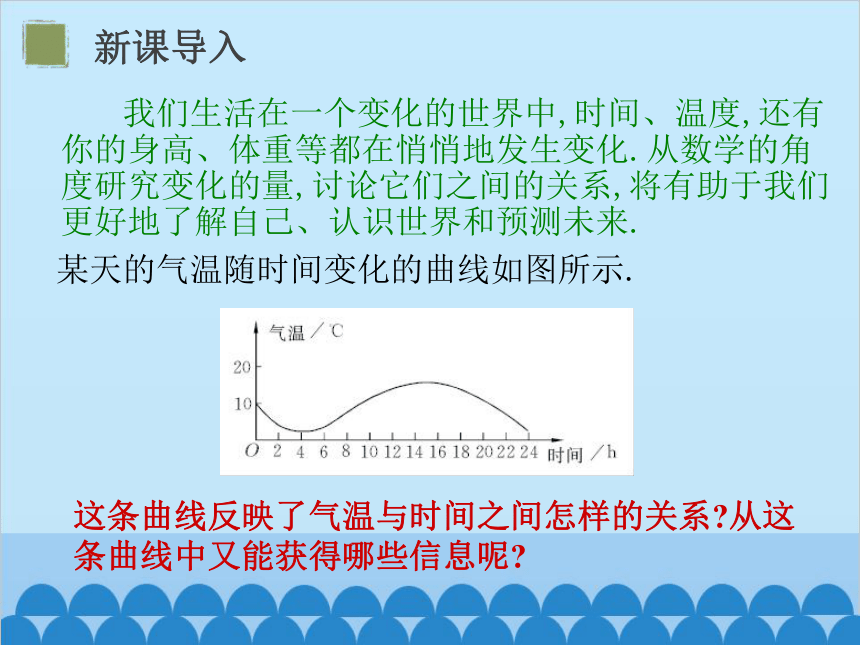
我们生活在一个变化的世界中,时间、温度,还有你的身高、体重等都在悄悄地发生变化.从数学的角度研究变化的量,讨论它们之间的关系,将有助于我们更好地了解自己、认识世界和预测未来.
某天的气温随时间变化的曲线如图所示.
这条曲线反映了气温与时间之间怎样的关系 从这条曲线中又能获得哪些信息呢
新课导入
讲授新知
贰
问题1:你坐过摩天轮吗?想一想,如果你坐在摩天轮上时,随着时间的变化,你离开地面的高度是如何变化的?
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
根据图象填表:
t/分 0 1 2 3 4 5 ……
h/米 ……
10
37
45
37
3
右图反映了旋转时间t(分)与摩天轮上的一点的高度h (米)之间的关系.
10
讲授新知
对于给定的时间 t ,相应的高度 h 确定吗?
本题中反应了哪两个变量之间的关系?
旋转时间t(分)与摩天轮上的一点的高度h
对于给定的时间 t ,相应的高度 h随之确定。
讲授新知
问题2:瓶子或罐头盒等圆柱形的物体,常常如图摆放。
1、随着层数的增加,物体的总数将如何变化?
2、请填写下表:
层数n 1 2 3 4 5 ……
物体总数y ……
3
6
10
15
1
讲授新知
对于给定的层数 n ,相应的物体总数 y 确定吗?
想一想
本题中反应了哪两个变量之间的关系?
层数 n与物体总数 y
对于给定的层数 n ,相应的物体总数 y随之确定。
讲授新知
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43 ℃ ,-27 ℃ ,0 ℃ ,18 ℃时,相应的热力学温度T是多少?
(2)给定一个大于-273 ℃的t值,你能求出相应的T值吗?
230K, 246K, 273K, 291K
讲授新知
本题中反应了哪两个变量之间的关系?
摄氏温度t( ℃)与热力学温度T(K)。
对于给定的一个t值,你能求出相应的T值吗?这个T值确定吗?唯一吗?
讲授新知
对于给定的一个t值,可以求出相应的T值,这个T值确定且唯一.
上面的三个问题中,有什么共同特点?
①时间 t 、高度 h ;
②层数n、物体总数y;
③摄氏温度t、热力学温度T。
都有两个变量。
注意:给定其中某一个变量的值,相应地就确定了另一个变量的值。
讲授新知
在某一变化过程中,有 变量x和y,并且对于变量x的每一个值,变量y都有 的值与它对应,那么我们就称y是x的函数,其中x是自变量,y是因变量。
一个x值
一个y值
y就是x的函数
对应
函数的概念:
即:
讲授新知
两个
唯一
回顾摩天轮,h是t的
函数吗?
引伸:t是h的函数吗?
每个时间t都只有一个h
和它对应,h就是t的
函数
当高度h为30时,对应的时间t多个。
所以t不是h的函数
判断甲变量是否是乙变量的函数,就看乙变量取一个值时,
甲变量是否只有唯一值和它对应.
讲授新知
y与x 的图象如图所示,问y是x的函数吗?
x
y
o
1
2
-2
不是。
由图可知,当x取1时,有两个y值与之对应,所以y不是x的函数.
讲授新知
【练习】
那么,以上三个问题,都用到了什么方法来表示函数呢?
讲授新知
根据图象填表:
t/分 0 1 2 3 4 5 ……
h/米 ……
11
11
37
45
37
3
问题1:下图反映了旋转时间t(分)与摩天轮上的一点的高度h (米)之间的关系。
图象法、
列表法
函数的表示法:
讲授新知
问题2:罐头盒等圆柱形的物体常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n 1 2 3 4 5 ……
物体总数y ……
6
10
15
1
3
讲授新知
函数的表示法:
列表法
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
函数的表示法:
关系式法(解析式法)
讲授新知
函数的表示法
(1)图象法
(2)列表法
(3)关系式法
思考:
对于问题2,你能用关系式法来表示吗?
三种表达形式都
可以相互转化
讲授新知
上述的三个问题中,自变量能取哪些值?
讲授新知
问题1:下图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系。
t/分 0 1 2 3 4 5 ……
h/米 ……
11
37
45
37
3
10
根据上图填表:
t≥0
自变量t的取值范围 。
讲授新知
问题2:罐头盒等圆柱形的物体常常如下图那样堆放。
随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n 1 2 3 4 5 ……
物体总数y ……
6
10
15
1
3
自变量n的取值范围 。
n取正整数
讲授新知
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
自变量t的取值范围 。
t≥-273℃
讲授新知
1、上述的三个问题中,自变量能取哪些值?
注意:对于实际问题中,自变量的取值应使实际问题有意义。
2、什么叫函数值?如何求函数值?
讲授新知
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值。
范例应用
解析:要判断一个关系式是不是函数,首先看这个变化过程中是否只有两个变量,其次看每一个x的值是否对应唯一确定的y值.
解:(1)此关系式只有两个变量,且每一个x值对应唯一的一个y值,故y是x的函数.
(2)此关系式中有三个变量,因此y不是x的函数.
(3)此关系式中虽然只有两个变量,但对于每一个确定的x值(x>0)对应的都有2个y值,如当x=4时,y=±2,故y不是x的函数.
(4)对于每个确定的x值(x>0)对应的都有2个y值,如当x=9时,y=±3,故y不是x的函数.
范例应用
由函数的定义可知在某个变化过程中,有两个变量x和y,对于每一个确定的x值,y值都有且只有一个值与之对应,当x值取不同的值时,y的值可以相等也可以不相等,但如果一个x的值对应着两个不同的y值,那么y一定不是x的函数.根据这一点,我们可以判定一个关系式是否表示函数.
小结
当堂训练
叁
当堂训练
1.(2021哈尔滨)周日,小辉从家步行到图书馆读书,读了一段时间后,小辉立刻按原路回家.在整个过程中,小辉离家的距离s(单位:m)与他所用的时间t(单位:min)之间的关系如图所示,则小辉从家去图书馆的速度和从图书馆回家的速度分别为( )
A.75m/min,90m/min B.80m/min,90m/min
C.75m/min,100m/min D.80m/min,100m/min
C
2.(2019柳州)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )
A.y=4x(x≥0) B.y=4x﹣3(x≥ )
C.y=3﹣4x(x≥0) D.y=3﹣4x(0≤x≤ )
D
当堂训练
3.表格列出了一项实验的统计数据,表示小球从高度x(单位:m)落下时弹跳高度y(单位:m)与下落高度x的关系,据表可以写出的一个关系式是 .
y=0.5x
当堂训练
(1)
(2)
(3)
4.下列式子中的y是x的函数吗?为什么?若y不是x的函数,怎样改变,才能使y是x的函数?
解:(1)、(2)中y是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应;(3)中,y不是x的函数,因为对于x的每一个确定的值,y都有两个确定的值与其对应.将关系式改为 或 ,都能使y是x的函数.
当堂训练
5.变量x与y的对应关系如下表所示:
x 1 4 9 16 25 …
y ±1 ±2 ±3 ±4 ±5 …
问:变量y是x的函数吗?为什么?若要使y是x的函数,可以怎样改动表格?
解:y不是x的函数,因为对于x的每一个确定的值,y都有两个确定的值与其对应. 要使y是x的函数,可以将表格中y的每一个值中的“±”改为“+”或“-”.
当堂训练
课堂小结
肆
1、函数的概念
2、函数的表示方法:
3、函数的自变量的取值范围
4、函数值的求法
(1)图象法
(2)列表法
(3)关系式法
课堂小结
课后作业
基础题:1.课后习题 4.1第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
第四章 一次函数
1 函数
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
我们生活在一个变化的世界中,时间、温度,还有你的身高、体重等都在悄悄地发生变化.从数学的角度研究变化的量,讨论它们之间的关系,将有助于我们更好地了解自己、认识世界和预测未来.
某天的气温随时间变化的曲线如图所示.
这条曲线反映了气温与时间之间怎样的关系 从这条曲线中又能获得哪些信息呢
新课导入
讲授新知
贰
问题1:你坐过摩天轮吗?想一想,如果你坐在摩天轮上时,随着时间的变化,你离开地面的高度是如何变化的?
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
O 1 2 3 4 5 6 7 8 9 10 11 12
3
10
37
45
h(米)
t(分)
讲授新知
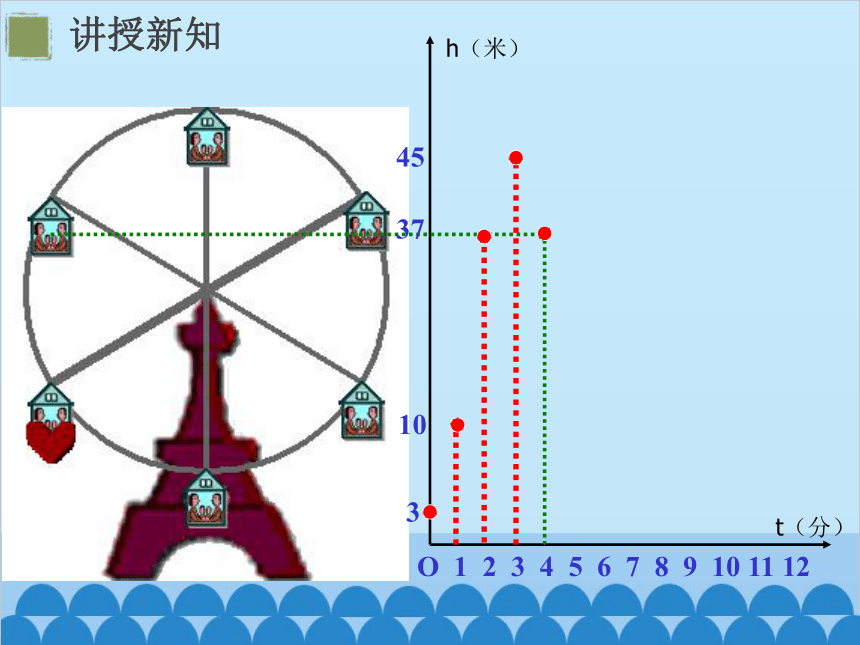
根据图象填表:
t/分 0 1 2 3 4 5 ……
h/米 ……
10
37
45
37
3
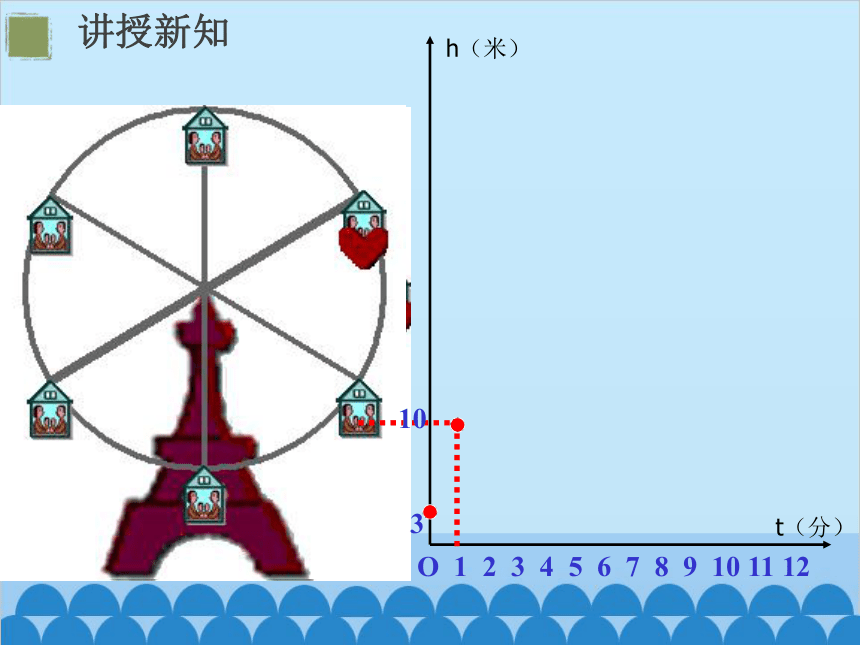
右图反映了旋转时间t(分)与摩天轮上的一点的高度h (米)之间的关系.
10
讲授新知
对于给定的时间 t ,相应的高度 h 确定吗?
本题中反应了哪两个变量之间的关系?
旋转时间t(分)与摩天轮上的一点的高度h
对于给定的时间 t ,相应的高度 h随之确定。
讲授新知
问题2:瓶子或罐头盒等圆柱形的物体,常常如图摆放。
1、随着层数的增加,物体的总数将如何变化?
2、请填写下表:
层数n 1 2 3 4 5 ……
物体总数y ……
3
6
10
15
1
讲授新知
对于给定的层数 n ,相应的物体总数 y 确定吗?
想一想
本题中反应了哪两个变量之间的关系?
层数 n与物体总数 y
对于给定的层数 n ,相应的物体总数 y随之确定。
讲授新知
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43 ℃ ,-27 ℃ ,0 ℃ ,18 ℃时,相应的热力学温度T是多少?
(2)给定一个大于-273 ℃的t值,你能求出相应的T值吗?
230K, 246K, 273K, 291K
讲授新知
本题中反应了哪两个变量之间的关系?
摄氏温度t( ℃)与热力学温度T(K)。
对于给定的一个t值,你能求出相应的T值吗?这个T值确定吗?唯一吗?
讲授新知
对于给定的一个t值,可以求出相应的T值,这个T值确定且唯一.
上面的三个问题中,有什么共同特点?
①时间 t 、高度 h ;
②层数n、物体总数y;
③摄氏温度t、热力学温度T。
都有两个变量。
注意:给定其中某一个变量的值,相应地就确定了另一个变量的值。
讲授新知
在某一变化过程中,有 变量x和y,并且对于变量x的每一个值,变量y都有 的值与它对应,那么我们就称y是x的函数,其中x是自变量,y是因变量。
一个x值
一个y值
y就是x的函数
对应
函数的概念:
即:
讲授新知
两个
唯一
回顾摩天轮,h是t的
函数吗?
引伸:t是h的函数吗?
每个时间t都只有一个h
和它对应,h就是t的
函数
当高度h为30时,对应的时间t多个。
所以t不是h的函数
判断甲变量是否是乙变量的函数,就看乙变量取一个值时,
甲变量是否只有唯一值和它对应.
讲授新知
y与x 的图象如图所示,问y是x的函数吗?
x
y
o
1
2
-2
不是。
由图可知,当x取1时,有两个y值与之对应,所以y不是x的函数.
讲授新知
【练习】
那么,以上三个问题,都用到了什么方法来表示函数呢?
讲授新知
根据图象填表:
t/分 0 1 2 3 4 5 ……
h/米 ……
11
11
37
45
37
3
问题1:下图反映了旋转时间t(分)与摩天轮上的一点的高度h (米)之间的关系。
图象法、
列表法
函数的表示法:
讲授新知
问题2:罐头盒等圆柱形的物体常常如下图那样堆放。随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n 1 2 3 4 5 ……
物体总数y ……
6
10
15
1
3
讲授新知
函数的表示法:
列表法
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
函数的表示法:
关系式法(解析式法)
讲授新知
函数的表示法
(1)图象法
(2)列表法
(3)关系式法
思考:
对于问题2,你能用关系式法来表示吗?
三种表达形式都
可以相互转化
讲授新知
上述的三个问题中,自变量能取哪些值?
讲授新知
问题1:下图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系。
t/分 0 1 2 3 4 5 ……
h/米 ……
11
37
45
37
3
10
根据上图填表:
t≥0
自变量t的取值范围 。
讲授新知
问题2:罐头盒等圆柱形的物体常常如下图那样堆放。
随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n 1 2 3 4 5 ……
物体总数y ……
6
10
15
1
3
自变量n的取值范围 。
n取正整数
讲授新知
问题3:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
自变量t的取值范围 。
t≥-273℃
讲授新知
1、上述的三个问题中,自变量能取哪些值?
注意:对于实际问题中,自变量的取值应使实际问题有意义。
2、什么叫函数值?如何求函数值?
讲授新知
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值。
范例应用
解析:要判断一个关系式是不是函数,首先看这个变化过程中是否只有两个变量,其次看每一个x的值是否对应唯一确定的y值.
解:(1)此关系式只有两个变量,且每一个x值对应唯一的一个y值,故y是x的函数.
(2)此关系式中有三个变量,因此y不是x的函数.
(3)此关系式中虽然只有两个变量,但对于每一个确定的x值(x>0)对应的都有2个y值,如当x=4时,y=±2,故y不是x的函数.
(4)对于每个确定的x值(x>0)对应的都有2个y值,如当x=9时,y=±3,故y不是x的函数.
范例应用
由函数的定义可知在某个变化过程中,有两个变量x和y,对于每一个确定的x值,y值都有且只有一个值与之对应,当x值取不同的值时,y的值可以相等也可以不相等,但如果一个x的值对应着两个不同的y值,那么y一定不是x的函数.根据这一点,我们可以判定一个关系式是否表示函数.
小结
当堂训练
叁
当堂训练
1.(2021哈尔滨)周日,小辉从家步行到图书馆读书,读了一段时间后,小辉立刻按原路回家.在整个过程中,小辉离家的距离s(单位:m)与他所用的时间t(单位:min)之间的关系如图所示,则小辉从家去图书馆的速度和从图书馆回家的速度分别为( )
A.75m/min,90m/min B.80m/min,90m/min
C.75m/min,100m/min D.80m/min,100m/min
C
2.(2019柳州)已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )
A.y=4x(x≥0) B.y=4x﹣3(x≥ )
C.y=3﹣4x(x≥0) D.y=3﹣4x(0≤x≤ )
D
当堂训练
3.表格列出了一项实验的统计数据,表示小球从高度x(单位:m)落下时弹跳高度y(单位:m)与下落高度x的关系,据表可以写出的一个关系式是 .
y=0.5x
当堂训练
(1)
(2)
(3)
4.下列式子中的y是x的函数吗?为什么?若y不是x的函数,怎样改变,才能使y是x的函数?
解:(1)、(2)中y是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应;(3)中,y不是x的函数,因为对于x的每一个确定的值,y都有两个确定的值与其对应.将关系式改为 或 ,都能使y是x的函数.
当堂训练
5.变量x与y的对应关系如下表所示:
x 1 4 9 16 25 …
y ±1 ±2 ±3 ±4 ±5 …
问:变量y是x的函数吗?为什么?若要使y是x的函数,可以怎样改动表格?
解:y不是x的函数,因为对于x的每一个确定的值,y都有两个确定的值与其对应. 要使y是x的函数,可以将表格中y的每一个值中的“±”改为“+”或“-”.
当堂训练
课堂小结
肆
1、函数的概念
2、函数的表示方法:
3、函数的自变量的取值范围
4、函数值的求法
(1)图象法
(2)列表法
(3)关系式法
课堂小结
课后作业
基础题:1.课后习题 4.1第 1,2题。
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
谢
谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
