运用公式法1[下学期]
图片预览






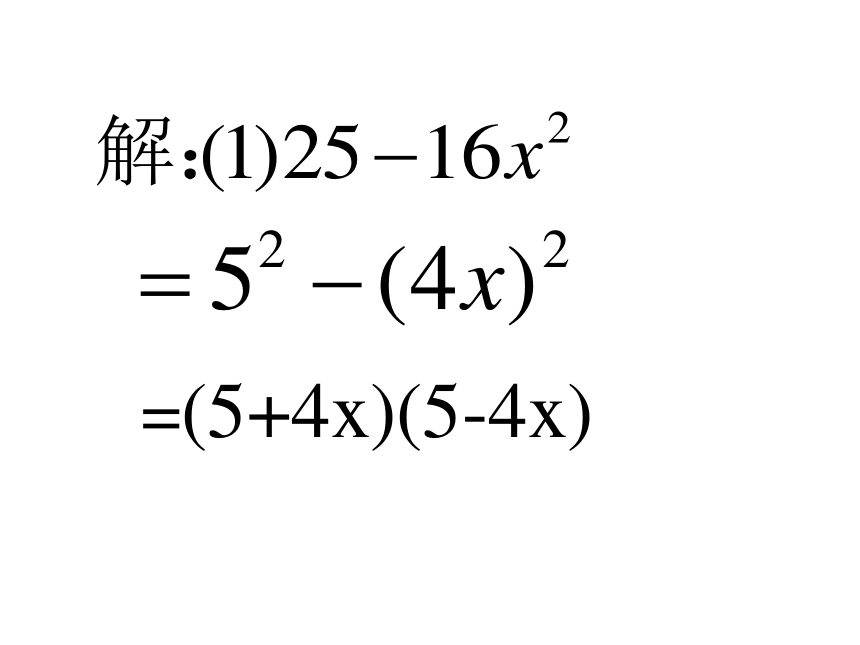
文档简介
课件23张PPT。第二章第三节
运用公式法(一)1.什么叫分解因式?2 . 如何用提公因式法进行因式分解?3. 因式分解的结果一般应符合哪些要求?回顾与思考:学习目标:1、了解用公式法分解因式的意义2、掌握用平方差公式分解因式3、了解提公因式法是分解因式的首先考虑的方法,再考虑用平法差公式分解因式a2-b2=(a+b)(a-b) (分解因式)(a+b)(a-b)= a2-b2 (整式的乘法)
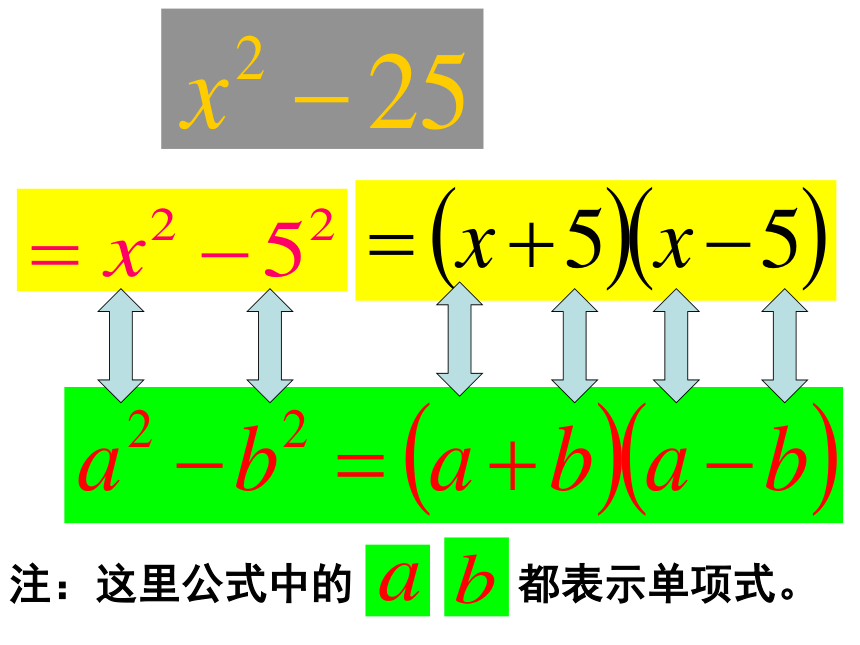
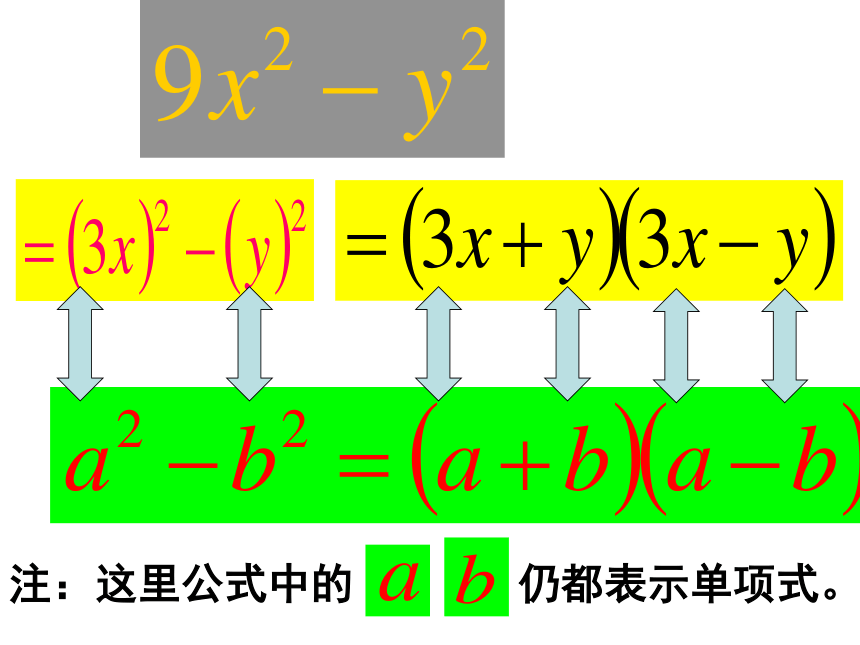
平方差公式观察与思考(1) 多项式 和 他们有什么共同特征? (2)尝试将它们分别写成两个因式的乘积,.注:这里公式中的都表示单项式。注:这里公式中的仍都表示单项式。例1:把下列各式分解因式=(5+4x)(5-4x)例2 :把下列各式分解因式
=(3m+3n+m-n)(3m+3n-m+n)=(4m+2n)(2m+4n)=4(2m+n)(m+2n)通过做第(2)小题你总结出什么经验来了吗?当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步分解因式.课堂练习:判断下列分解因式是否正确:××××× 练习:如图,在一块边长为acm的正方形纸片的四角,各剪去一个边长为bcm的正方形,求剩余部分的面积。a=3.6,b=0.8,计算剩余部分面积. 原式=(3.6+2×0.8)×(3.6-2×0.8)
=10.4解:
=(a+2b)(a-2b)当a=3.6,b=0.8时课堂小结1、先判断一个多项式是否符合平方差公式的特点,若符合,又没有公因式,则先把各项正确地写成一个完全平方的形式,再使用公式。2、如果多项式各项含有公因式,则第一步是提公因式,然后看是否符合平方差公式的特点,若符合继续进行。3、第一步分解以后,所含的多项式还可以继续分解,则需要进一步分解因式,直到每个多项式都不能分解为止。 思考:(1)对于任意整数n,多项式 能被哪个数整除? (2)解方程谢谢,再见!
运用公式法(一)1.什么叫分解因式?2 . 如何用提公因式法进行因式分解?3. 因式分解的结果一般应符合哪些要求?回顾与思考:学习目标:1、了解用公式法分解因式的意义2、掌握用平方差公式分解因式3、了解提公因式法是分解因式的首先考虑的方法,再考虑用平法差公式分解因式a2-b2=(a+b)(a-b) (分解因式)(a+b)(a-b)= a2-b2 (整式的乘法)
平方差公式观察与思考(1) 多项式 和 他们有什么共同特征? (2)尝试将它们分别写成两个因式的乘积,.注:这里公式中的都表示单项式。注:这里公式中的仍都表示单项式。例1:把下列各式分解因式=(5+4x)(5-4x)例2 :把下列各式分解因式
=(3m+3n+m-n)(3m+3n-m+n)=(4m+2n)(2m+4n)=4(2m+n)(m+2n)通过做第(2)小题你总结出什么经验来了吗?当多项式的各项含有公因式时,通常先提出这个公因式,然后再进一步分解因式.课堂练习:判断下列分解因式是否正确:××××× 练习:如图,在一块边长为acm的正方形纸片的四角,各剪去一个边长为bcm的正方形,求剩余部分的面积。a=3.6,b=0.8,计算剩余部分面积. 原式=(3.6+2×0.8)×(3.6-2×0.8)
=10.4解:
=(a+2b)(a-2b)当a=3.6,b=0.8时课堂小结1、先判断一个多项式是否符合平方差公式的特点,若符合,又没有公因式,则先把各项正确地写成一个完全平方的形式,再使用公式。2、如果多项式各项含有公因式,则第一步是提公因式,然后看是否符合平方差公式的特点,若符合继续进行。3、第一步分解以后,所含的多项式还可以继续分解,则需要进一步分解因式,直到每个多项式都不能分解为止。 思考:(1)对于任意整数n,多项式 能被哪个数整除? (2)解方程谢谢,再见!
