配方法解一元二次方程3个课时的课件[下学期]
文档属性
| 名称 | 配方法解一元二次方程3个课时的课件[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 659.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-14 08:09:00 | ||
图片预览









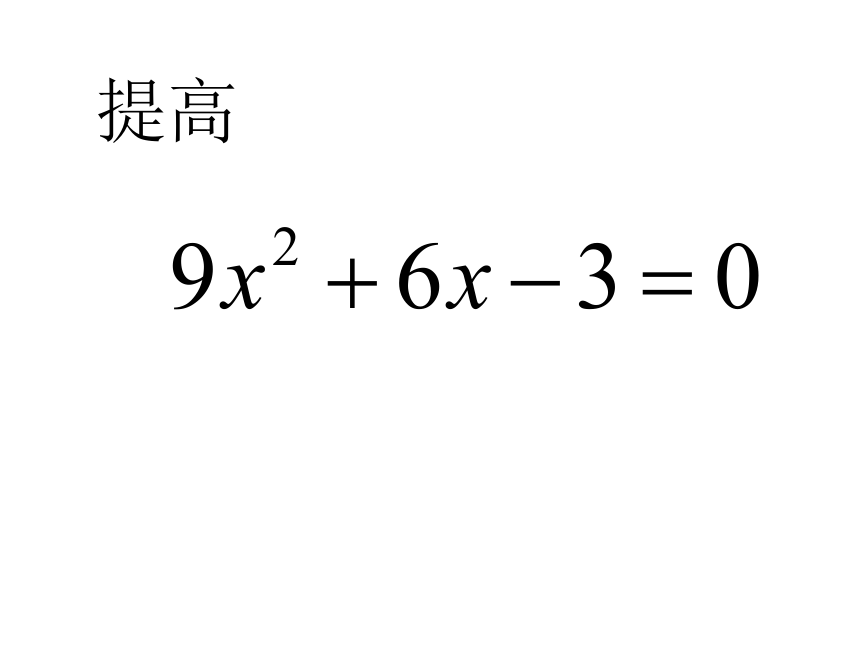

文档简介
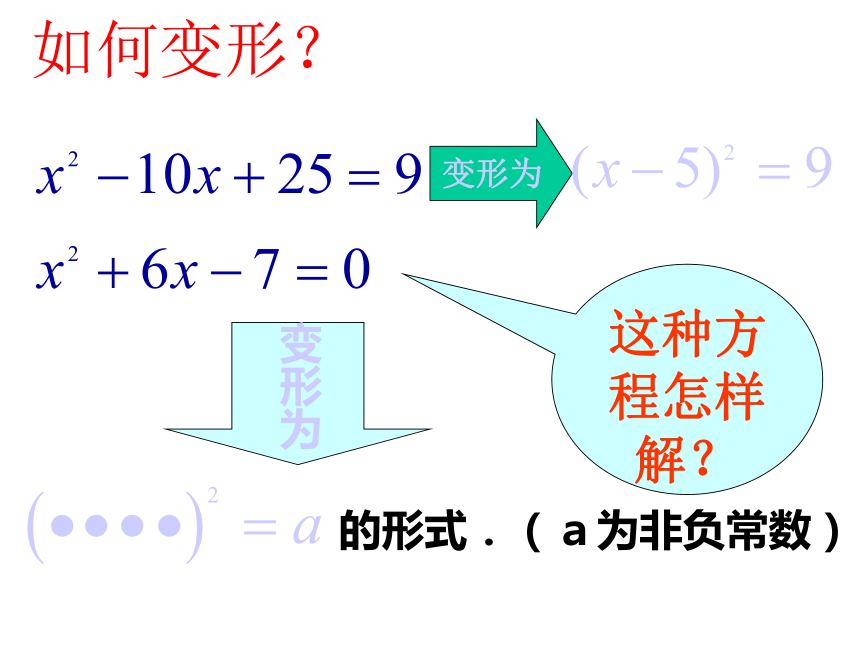
课件32张PPT。一元二次方程的解法配方法1一般地,对于形如
的方程,根据平方根的意义,可解得什么?
巩固练习1.方程 的根是 ;
2.方程 的根是
3.方程 的是 ;这种方程怎样解?变形为的形式.(a为非负常数)变形为如何变形?2、请说出完全平方公式 根据完全平方公式填空(格式如题(1))(1)
(2)
(3)
(4)424525把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.参照第一题,
推想一下第二题及第三题的解法(1)
(2)
(3)例题1用配方法解下列一元二次方程例2、用配方法解下列方程: (1)
(2)提高谈收获! ---配方法2一元二次方程的解法开心练一练: (1) (2)2、下列方程能用直接开平方法来解吗?创设情境 温故探新1、用直接开平方法解下列方程:静心想一想:(1)(2)(3)能否把(3)转化成(x+b)2=a(a≥0)的
形式呢?(1)(2)(3)=( + )2=( )2=( )2左边:所填常数等于一次项系数一半的平方.右边:所填常数等于一次项系数的一半.填上适当的数或式,使下列各等式成立.大胆试一试:共同点: ( )2=( )2(4)合作交流探究新知自主探究观察(1)(2)看所填的常数与一次项系数之间有什么关系?(1)(2)的结论适合于(3)吗? 适用于(4)吗?现在你会解方程 吗?把常数项移到方程右边得:两边同加上 得: 即两边直接开平方得:合作交流探究新知
解:∴原方程的解为自主探究如何配方?例1: 用配方法解方程解:配方得:开平方得:范例研讨运用新知移项得:∴原方程的解为:一次项系数变为负又如何配方呢?例2: 你能用配方法解方程
吗?解:配方得:开平方得:范例研讨运用新知移项得:∴原方程的解为:化二次项系数为1得:二次项系数不为1
又怎么办?想一想用配方法
解一元二次方程
一般有哪些步骤?例2: 你能用配方法解方程
吗?反馈练习巩固新知= ( + )2= ( - )2(2)(1)( )1、填空:( )认真做一做: (3) ( ) = ( - )2 (4) ( ) = ( - )2你一定能行!反馈练习巩固新知2、用配方法解下列方程:3、用配方法将下列式子化成a(x+h)2+k的形式。 (1)x2+8x-15=0(2)x2-5x-6=0(3)2x2-5x-6=0(4) x2+px+q=0(p2-4q> 0) (3) -3x2-2x+1 (2) x2-x+1 (1) y2+y-2课堂小结布置作业小结:(2)移项(3)配方(4)开平方
(5)写出方程的解
思考题:1.已知x是实数,求y=x2-4x+5的最小值.2、用配方法解一元二次方程 ax2+bx+c=0(a≠0) 的步骤:1、配方法: 通过配方,将方程的左边化成一个含未知数的完全平方式,右边是一个非负常数,运用直接开平方求出方程的解的方法。
2.已知x2+y2-4x+8y+20=0,灵活应用配方法求x+y的值.3.借助配方法任写一个代数式使它的值恒大于0.(1)化二次项系数为1今天你有哪些收获?九年级数学(上)第22章 一元二次方程一元二次方程的解法:配方法(3)
配方法我们通过配成完全平方式的方法,得到了一元二次方程的根,这种解一元二次方程的方法称为配方法(solving by completing the square)平方根的意义:完全平方式:式子a2±2ab+b2叫完全平方式,且a2±2ab+b2 =(a±b)2. 如果x2=a,那么x=用配方法解一元二次方程的方法的助手:配方法用配方法解一元二次方程的步骤:1.移项:把常数项移到方程的右边;
2.配方:方程两边都加上一次项系数绝对值一半的平方;
3.变形:方程左分解因式,右边合并同类;
4.开方:根据平方根意义,方程两边开平方;
5.求解:解一元一次方程;
6.定解:写出原方程的解.你能行吗用配方法解下列方程.
1.x2 – 2 = 0;
2.x2 -3x- =0 ;
3.x2+4x=2;
4.x2-6x+1=0 ; 5.3x2 +8x –3=0 ; 这个方程与前4个方程不一样的是二次项系数不是1,而是3.基本思想是:
如果能转化为前4个方程的形式,则问题即可解决.你想到了什么办法?配方法 例2 解方程 3x2+8x-3=0. 1.化1:把二次项系数化为1;3.配方:方程两边都加上一次项系数绝对值一半的平方;4.变形:方程左分解因式,右边合并同类;5.开方:根据平方根意义,方程两边开平方;6.求解:解一元一次方程;7.定解:写出原方程的解.2.移项:把常数项移到方程的右边;成功者是你吗用配方法解下列方程.
4x2 - 12x - 1 = 0 ;
3x2 + 2x – 3 = 0 ;
4x2+4x+10 =1-8x;
-3x2+22x-24=0.你能行吗做一做
一小球以15m/s的初速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:
h=15t-5t2 .
小球何时能达到10m的高度?回味无穷本节课复习了哪些旧知识呢?
请两个“老朋友”助阵和加深对“配方法”的理解运用:
平方根的意义:
完全平方式:式子a2±2ab+b2叫完全平方式,且a2±2ab+b2 =(a±b)2.
本节课你又学会了哪些新知识呢?
用配方法解二次项系数不是1的一元二次方程的步骤:
1.化1:把二次项系数化为1(方程两边都除以二次项系数);
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
用一元二次方程这个模型来解答或解决生活中的一些问题(即列一元二次方程解应用题). 如果x2=a,那么x=知识的升华1.根据题意,列出方程并求解:1.如图,在一块长35m,宽26m矩形地面上,修建同样宽的两条互相垂直的道路,剩余部分栽种花草,在使剩余部分的面积为850m2,道路的宽应是多少?解:设道路的宽为 x m,根据题意得 (35-x) (26-x) =850.即x2 - 61x-60 =0.解这个方程,得x1 =1;
x2 =60(不合题意,舍去).答:道路的宽应为1m.知识的升华根据题意,列出方程并求解:2.印度古算书中有这样一首诗:“一群猴子分两队,高高兴兴在游戏,八分之一再平方,蹦蹦跳跳树林里;其余十二叽喳喳,伶俐活泼又调皮.告我总数共多少?”解:设总共有 x 只猴子,根据题意得 即x2 - 64x+768 =0.解这个方程,得x1 =48;
x2 =16.答:一共有猴子48只或者16只.知识的升华3. 解下列方程:
(1).6x2 -7x+ 1 = 0;
(2).5x2 -9x –18=0;
(3).4x 2 –3x =52;2. 参考答案:
的方程,根据平方根的意义,可解得什么?
巩固练习1.方程 的根是 ;
2.方程 的根是
3.方程 的是 ;这种方程怎样解?变形为的形式.(a为非负常数)变形为如何变形?2、请说出完全平方公式 根据完全平方公式填空(格式如题(1))(1)
(2)
(3)
(4)424525把一元二次方程的左边配成一个完全平方式,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.参照第一题,
推想一下第二题及第三题的解法(1)
(2)
(3)例题1用配方法解下列一元二次方程例2、用配方法解下列方程: (1)
(2)提高谈收获! ---配方法2一元二次方程的解法开心练一练: (1) (2)2、下列方程能用直接开平方法来解吗?创设情境 温故探新1、用直接开平方法解下列方程:静心想一想:(1)(2)(3)能否把(3)转化成(x+b)2=a(a≥0)的
形式呢?(1)(2)(3)=( + )2=( )2=( )2左边:所填常数等于一次项系数一半的平方.右边:所填常数等于一次项系数的一半.填上适当的数或式,使下列各等式成立.大胆试一试:共同点: ( )2=( )2(4)合作交流探究新知自主探究观察(1)(2)看所填的常数与一次项系数之间有什么关系?(1)(2)的结论适合于(3)吗? 适用于(4)吗?现在你会解方程 吗?把常数项移到方程右边得:两边同加上 得: 即两边直接开平方得:合作交流探究新知
解:∴原方程的解为自主探究如何配方?例1: 用配方法解方程解:配方得:开平方得:范例研讨运用新知移项得:∴原方程的解为:一次项系数变为负又如何配方呢?例2: 你能用配方法解方程
吗?解:配方得:开平方得:范例研讨运用新知移项得:∴原方程的解为:化二次项系数为1得:二次项系数不为1
又怎么办?想一想用配方法
解一元二次方程
一般有哪些步骤?例2: 你能用配方法解方程
吗?反馈练习巩固新知= ( + )2= ( - )2(2)(1)( )1、填空:( )认真做一做: (3) ( ) = ( - )2 (4) ( ) = ( - )2你一定能行!反馈练习巩固新知2、用配方法解下列方程:3、用配方法将下列式子化成a(x+h)2+k的形式。 (1)x2+8x-15=0(2)x2-5x-6=0(3)2x2-5x-6=0(4) x2+px+q=0(p2-4q> 0) (3) -3x2-2x+1 (2) x2-x+1 (1) y2+y-2课堂小结布置作业小结:(2)移项(3)配方(4)开平方
(5)写出方程的解
思考题:1.已知x是实数,求y=x2-4x+5的最小值.2、用配方法解一元二次方程 ax2+bx+c=0(a≠0) 的步骤:1、配方法: 通过配方,将方程的左边化成一个含未知数的完全平方式,右边是一个非负常数,运用直接开平方求出方程的解的方法。
2.已知x2+y2-4x+8y+20=0,灵活应用配方法求x+y的值.3.借助配方法任写一个代数式使它的值恒大于0.(1)化二次项系数为1今天你有哪些收获?九年级数学(上)第22章 一元二次方程一元二次方程的解法:配方法(3)
配方法我们通过配成完全平方式的方法,得到了一元二次方程的根,这种解一元二次方程的方法称为配方法(solving by completing the square)平方根的意义:完全平方式:式子a2±2ab+b2叫完全平方式,且a2±2ab+b2 =(a±b)2. 如果x2=a,那么x=用配方法解一元二次方程的方法的助手:配方法用配方法解一元二次方程的步骤:1.移项:把常数项移到方程的右边;
2.配方:方程两边都加上一次项系数绝对值一半的平方;
3.变形:方程左分解因式,右边合并同类;
4.开方:根据平方根意义,方程两边开平方;
5.求解:解一元一次方程;
6.定解:写出原方程的解.你能行吗用配方法解下列方程.
1.x2 – 2 = 0;
2.x2 -3x- =0 ;
3.x2+4x=2;
4.x2-6x+1=0 ; 5.3x2 +8x –3=0 ; 这个方程与前4个方程不一样的是二次项系数不是1,而是3.基本思想是:
如果能转化为前4个方程的形式,则问题即可解决.你想到了什么办法?配方法 例2 解方程 3x2+8x-3=0. 1.化1:把二次项系数化为1;3.配方:方程两边都加上一次项系数绝对值一半的平方;4.变形:方程左分解因式,右边合并同类;5.开方:根据平方根意义,方程两边开平方;6.求解:解一元一次方程;7.定解:写出原方程的解.2.移项:把常数项移到方程的右边;成功者是你吗用配方法解下列方程.
4x2 - 12x - 1 = 0 ;
3x2 + 2x – 3 = 0 ;
4x2+4x+10 =1-8x;
-3x2+22x-24=0.你能行吗做一做
一小球以15m/s的初速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:
h=15t-5t2 .
小球何时能达到10m的高度?回味无穷本节课复习了哪些旧知识呢?
请两个“老朋友”助阵和加深对“配方法”的理解运用:
平方根的意义:
完全平方式:式子a2±2ab+b2叫完全平方式,且a2±2ab+b2 =(a±b)2.
本节课你又学会了哪些新知识呢?
用配方法解二次项系数不是1的一元二次方程的步骤:
1.化1:把二次项系数化为1(方程两边都除以二次项系数);
2.移项:把常数项移到方程的右边;
3.配方:方程两边都加上一次项系数绝对值一半的平方;
4.变形:方程左分解因式,右边合并同类;
5.开方:根据平方根意义,方程两边开平方;
6.求解:解一元一次方程;
7.定解:写出原方程的解.
用一元二次方程这个模型来解答或解决生活中的一些问题(即列一元二次方程解应用题). 如果x2=a,那么x=知识的升华1.根据题意,列出方程并求解:1.如图,在一块长35m,宽26m矩形地面上,修建同样宽的两条互相垂直的道路,剩余部分栽种花草,在使剩余部分的面积为850m2,道路的宽应是多少?解:设道路的宽为 x m,根据题意得 (35-x) (26-x) =850.即x2 - 61x-60 =0.解这个方程,得x1 =1;
x2 =60(不合题意,舍去).答:道路的宽应为1m.知识的升华根据题意,列出方程并求解:2.印度古算书中有这样一首诗:“一群猴子分两队,高高兴兴在游戏,八分之一再平方,蹦蹦跳跳树林里;其余十二叽喳喳,伶俐活泼又调皮.告我总数共多少?”解:设总共有 x 只猴子,根据题意得 即x2 - 64x+768 =0.解这个方程,得x1 =48;
x2 =16.答:一共有猴子48只或者16只.知识的升华3. 解下列方程:
(1).6x2 -7x+ 1 = 0;
(2).5x2 -9x –18=0;
(3).4x 2 –3x =52;2. 参考答案:
同课章节目录
