矩形[下学期]

课件15张PPT。课题：矩形

姓名：嘉绒降措 课题：矩形教学目标:1.让学生在以前学过的长方形的基础上更深刻的认识矩形。
2.让学生掌握矩形的性质定理和判定定理。
教学重点:1.矩形的性质定理。
2.矩形的判定定理。
教学难点：矩形的性质定理和判定定理。
课型：新课。
教学方法：启发式。
教学过程：一.复习引入：
平行四边形的定义….
平行四边行的性质….
平行四边行的判定定理…..回忆平行四边行返回定义：二组对边互相平行的四边行。
性质:1.平行四边行两组对角相等。
2.平行四边行两组对边互相平行。
3.平行四边行对角线互相平分。
判定定理：
1.两组对角分别相等的四边形是平行四边行。
2.两组对边互相平行的四边行是平行四边行。
3.对角线互相平分的四边形是平行四边行。

矩形定义：有一个角是直角的平行四边形
矩形性质一：矩形的四个角都是直角。
矩形性质二：矩形的对角线相等。
矩形判定定理一：有三个角是直角的四边形是 矩形。
矩形判定定理二：对角线相等的平行四边行是 矩形。
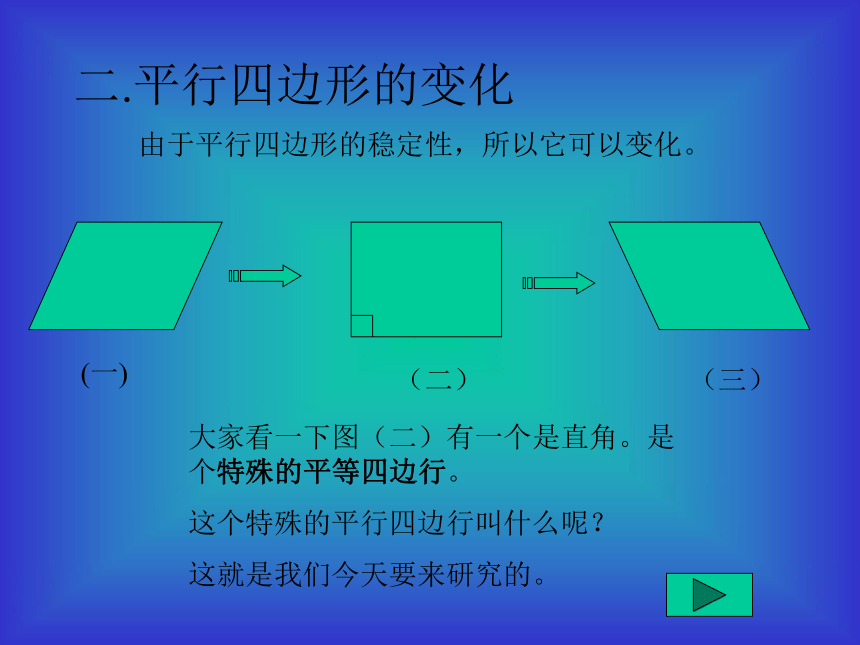
返回二.平行四边形的变化 由于平行四边形的稳定性，所以它可以变化。(一)（三）（二）大家看一下图（二）有一个是直角。是个特殊的平等四边行。
这个特殊的平行四边行叫什么呢？
这就是我们今天要来研究的。矩形以下图形都是矩形大家观察下：思考它们有什么共同特征？一.矩形定义定义：有一个角是直角的平行四边形

大家看一下矩形ABCD
观察它的特点。
并举几个现实中的例子。
二.矩形的性质大家观察矩形ABCD的角
大家会发现它的角。。。
全部都是直角！
（我们知道平行四边行的对角线是相互平分的。那么矩形的对角线有什么性质呢？）
矩形的对角线是否相等？（证明）
性质一：矩形的四个角都是直角。
矩形的对角线是否相等的证明已知:矩形ABCD求证：AC=DB
证明：矩形ABCD=> AB=DC BC=CB
=>△ABC =△DCB
=>AC=DB
性质二：矩形的对角线相等。
通过刚才的证明进一步的推出：OA=OB=OC 即：OB=1/2 AC
即推论：直角三角形的斜边上的中线等于斜边的一半。
三.矩形的判定定理 我们通过平行四边行的学习知道它的判定定理是由它的定义或性质定理推导而来。那我们同样由它的思路来看推导一下矩形的判定定理。
矩形性质一：矩形的四个角都是直角。

那我们接下来思考由矩形的性质二：矩形的对角线相等能不能反推过来呢？即：对角线相等的平行四边是否是矩形？
根据性质一很容易得到：
判定定理一：有三个角是直角的四边形是矩形。
对角线相等是否是矩形的证明已知：在平行四边形ABCD中 AC=DB 求证:平行四边形 ABCD是矩形。
证明：AC=BD BC=CB AB=CD
????????? => △ABC≌△DCB
?????????? ? => AB//DC
=> 平行四边ABCD是矩形。
即：矩形判定定理二：对角线相等的平行四边行是矩形。
四：练习已知：平行四边ABCD的对角线AC，BD相交于点O，△AOB是等边三角形AB=4CM 求：平行四边形ABCD的面积。
证明：ABCD是平行四边形
=> AO=1/2 AC BO=1/2 BD
△AOB等边三角形 =>AO=BO
=>AC=BC =>ABCD是矩形
在Rt△ABC中 AB=4 Cm, AC=2AO=2AB=8Cm

则：BC= （CM）
S ABCD=AB.BC=4* = 16 (CM)
小结,作业及预习小结:
矩形的定义…..
矩形的性质1….2…..
矩形的判定定理1….2…….
作业：课后习题：1，2，3
预习：下一节内容。
谢谢观赏! 完…….