华师大版数学八年级上册 第13章 小结与复习教案
文档属性
| 名称 | 华师大版数学八年级上册 第13章 小结与复习教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-23 00:00:00 | ||
图片预览


文档简介
第13章 小结与复习
1.让学生正确理解命题、定理与证明的有关知识,能灵活正确地解决全等三角形的相关问题;
2.会用尺规作图法作五种基本作图,掌握等腰三角形的性质与判定,让学生灵活地解决等腰三角形的相关问题;
3.让学生进一步理解线段的垂直平分线性质定理与判定定理,角平分线的性质定理与判定定理.
三角形的全等,等腰三角形的性质与判定,垂直平分线与角平分线的性质与判定.
三角形的全等,等腰三角形的性质与判定,垂直平分线与角平分线的性质与判定.
一、情境导入 整体感知
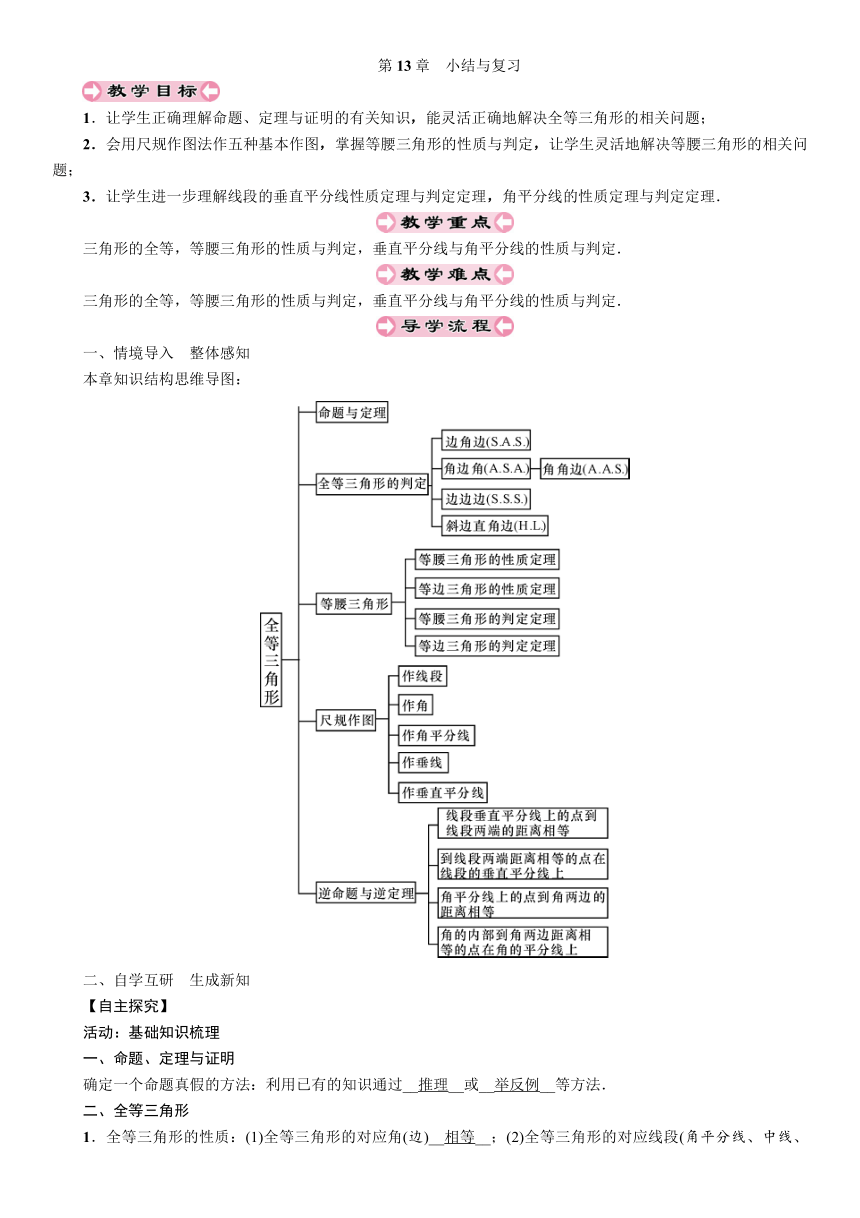
本章知识结构思维导图:
二、自学互研 生成新知
【自主探究】
活动:基础知识梳理
一、命题、定理与证明
确定一个命题真假的方法:利用已有的知识通过__推理__或__举反例__等方法.
二、全等三角形
1.全等三角形的性质:(1)全等三角形的对应角(边)__相等__;(2)全等三角形的对应线段(角平分线、中线、高)__相等__,周长__相等__,面积__相等__.
2.全等三角形的判定方法:__S.A.S.;A.S.A.;A.A.S.;S.S.S.;H.L.(仅适用于直角三角形)__.
三、等腰三角形的性质与判定
1.等腰三角形的性质:(1)两底角__相等__;(2)顶角的__角平分线__、底边上的__中线__和底边上的__高__互相重合.
2.等腰三角形的判定:等角对__等边__.
3.等边三角形的性质:等边三角形的各角都__相等__,并且都等于__60°__.
4.等边三角形的判定:(1)三个角都__相等__的三角形是等边三角形;(2)有一个角等于__60°__的等腰三角形是等边三角形;(3)有__三边相等__的三角形是等边三角形.
四、线段的垂直平分线与角平分线
1.线段的垂直平分线的性质定理:__线段垂直平分线上的点到线段两端点的距离相等__;
判定定理:__到线段两端距离相等的点在线段的垂直平分线上__.
2.角平分线的性质定理:__角平分线上的点到角两边的距离相等__;
判定定理:__到角两边距离相等的点在角的平分线上.
【师生活动】①明了学情:关注学生对本章各知识点的掌握情况;
②差异指导:对学生遗忘的知识及时引导、点拨,帮助学生查漏补缺;
③生生互助:学生小组内交流讨论,相互释疑,相互查漏补缺.
三、典例剖析 运用新知
【合作探究】
例1:判断下列命题的真假.
(1)同一平面内,垂直于同一直线的两条直线互相平行.(真命题)
(2)相等的两个角是对顶角.(假命题)
例2:已知:如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
证明:连结AD,
∵在△ABD和△ACD中
∴△ABD≌△ACD.
∴∠DAB=∠DAC.
∵DE⊥AB,DF⊥AC,
∴DE=DF.
例3:如图,已知在等边△ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC于M,求证:M是BE的中点.
证明:连结BD,
∵三角形ABC是等边三角形,D是AC的中点,∠DBC=∠ABC.
又∵CE=CD,所以∠CDE=∠E.
∴∠ACB=2∠E.
∴∠E=∠ACB.
∴∠DBC=∠E.
∴BD=DE,又DM⊥BC,垂足为M,
∴M是BE的中点.
四、课堂小结 回顾新知
通过本节课的复习,你对本章知识又有了哪些新的认识?还存在哪些疑惑?请说出你的想法和同学们一起分享!
五、检测反馈 落实新知
1.下列判断不正确的是(A)
A.形状相同的图形是全等图形
B.能够完全重合的两个三角形全等
C.全等图形的形状和大小都相同
D.全等三角形的对应角相等
2.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为(B)
A.2 B.3 C.5 D.2.5
,(第2题图)) ,(第3题图))
3.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连结BE,则∠CBE等于(C)
A.80° B.70° C.60° D.50°
4.如图:要测量河岸相对的两点A、B之间的距离,先从B处出发与AB成90°角方向,向前走50米 到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转90°沿DE方向再走17米,到达E处,使A、C与E在同一直线上,那么测得A、B的距离为__17__米.
5.如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足为C、D,连结CD交OE于点F.
求证:(1)OC=OD;
(2)OF⊥CD .
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=ED,在Rt△ECO和Rt△EDO中,
EO=EO,EC=ED,∴△ECO≌△EDO(H.L.)
∴OC=OD;
(2)由(1)知△OCD是等腰三角形,OF是△OCD的顶角平分线,∴OF⊥CD.
六、课后作业 巩固新知
见学生用书.
1.让学生正确理解命题、定理与证明的有关知识,能灵活正确地解决全等三角形的相关问题;
2.会用尺规作图法作五种基本作图,掌握等腰三角形的性质与判定,让学生灵活地解决等腰三角形的相关问题;
3.让学生进一步理解线段的垂直平分线性质定理与判定定理,角平分线的性质定理与判定定理.
三角形的全等,等腰三角形的性质与判定,垂直平分线与角平分线的性质与判定.
三角形的全等,等腰三角形的性质与判定,垂直平分线与角平分线的性质与判定.
一、情境导入 整体感知
本章知识结构思维导图:
二、自学互研 生成新知
【自主探究】
活动:基础知识梳理
一、命题、定理与证明
确定一个命题真假的方法:利用已有的知识通过__推理__或__举反例__等方法.
二、全等三角形
1.全等三角形的性质:(1)全等三角形的对应角(边)__相等__;(2)全等三角形的对应线段(角平分线、中线、高)__相等__,周长__相等__,面积__相等__.
2.全等三角形的判定方法:__S.A.S.;A.S.A.;A.A.S.;S.S.S.;H.L.(仅适用于直角三角形)__.
三、等腰三角形的性质与判定
1.等腰三角形的性质:(1)两底角__相等__;(2)顶角的__角平分线__、底边上的__中线__和底边上的__高__互相重合.
2.等腰三角形的判定:等角对__等边__.
3.等边三角形的性质:等边三角形的各角都__相等__,并且都等于__60°__.
4.等边三角形的判定:(1)三个角都__相等__的三角形是等边三角形;(2)有一个角等于__60°__的等腰三角形是等边三角形;(3)有__三边相等__的三角形是等边三角形.
四、线段的垂直平分线与角平分线
1.线段的垂直平分线的性质定理:__线段垂直平分线上的点到线段两端点的距离相等__;
判定定理:__到线段两端距离相等的点在线段的垂直平分线上__.
2.角平分线的性质定理:__角平分线上的点到角两边的距离相等__;
判定定理:__到角两边距离相等的点在角的平分线上.
【师生活动】①明了学情:关注学生对本章各知识点的掌握情况;
②差异指导:对学生遗忘的知识及时引导、点拨,帮助学生查漏补缺;
③生生互助:学生小组内交流讨论,相互释疑,相互查漏补缺.
三、典例剖析 运用新知
【合作探究】
例1:判断下列命题的真假.
(1)同一平面内,垂直于同一直线的两条直线互相平行.(真命题)
(2)相等的两个角是对顶角.(假命题)
例2:已知:如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
证明:连结AD,
∵在△ABD和△ACD中
∴△ABD≌△ACD.
∴∠DAB=∠DAC.
∵DE⊥AB,DF⊥AC,
∴DE=DF.
例3:如图,已知在等边△ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC于M,求证:M是BE的中点.
证明:连结BD,
∵三角形ABC是等边三角形,D是AC的中点,∠DBC=∠ABC.
又∵CE=CD,所以∠CDE=∠E.
∴∠ACB=2∠E.
∴∠E=∠ACB.
∴∠DBC=∠E.
∴BD=DE,又DM⊥BC,垂足为M,
∴M是BE的中点.
四、课堂小结 回顾新知
通过本节课的复习,你对本章知识又有了哪些新的认识?还存在哪些疑惑?请说出你的想法和同学们一起分享!
五、检测反馈 落实新知
1.下列判断不正确的是(A)
A.形状相同的图形是全等图形
B.能够完全重合的两个三角形全等
C.全等图形的形状和大小都相同
D.全等三角形的对应角相等
2.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为(B)
A.2 B.3 C.5 D.2.5
,(第2题图)) ,(第3题图))
3.如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连结BE,则∠CBE等于(C)
A.80° B.70° C.60° D.50°
4.如图:要测量河岸相对的两点A、B之间的距离,先从B处出发与AB成90°角方向,向前走50米 到C处立一根标杆,然后方向不变继续朝前走50米到D处,在D处转90°沿DE方向再走17米,到达E处,使A、C与E在同一直线上,那么测得A、B的距离为__17__米.
5.如图:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足为C、D,连结CD交OE于点F.
求证:(1)OC=OD;
(2)OF⊥CD .
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=ED,在Rt△ECO和Rt△EDO中,
EO=EO,EC=ED,∴△ECO≌△EDO(H.L.)
∴OC=OD;
(2)由(1)知△OCD是等腰三角形,OF是△OCD的顶角平分线,∴OF⊥CD.
六、课后作业 巩固新知
见学生用书.
