3.1.2函数的表示法(共16张PPT)
文档属性
| 名称 | 3.1.2函数的表示法(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 873.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 16:26:04 | ||
图片预览



文档简介
(共16张PPT)
3.1.2
必修第一册
函数的表示法
XXX学校 XXX
2023.09
00
回顾
函数的表示方法通常有 种,它们是 ____________ 、____________和_____________.
列表法
图像法
解析法
三
【解析法】通过数学表达式表示两个变量之间的对应关系.
正比例函数
反比例函数
一次函数
二次函数
解析法的优点:简明概括了变量间的关系,通过解析式求任意一个函数值
解析法的缺点:并不是所有函数都有解析式。
函数解析式
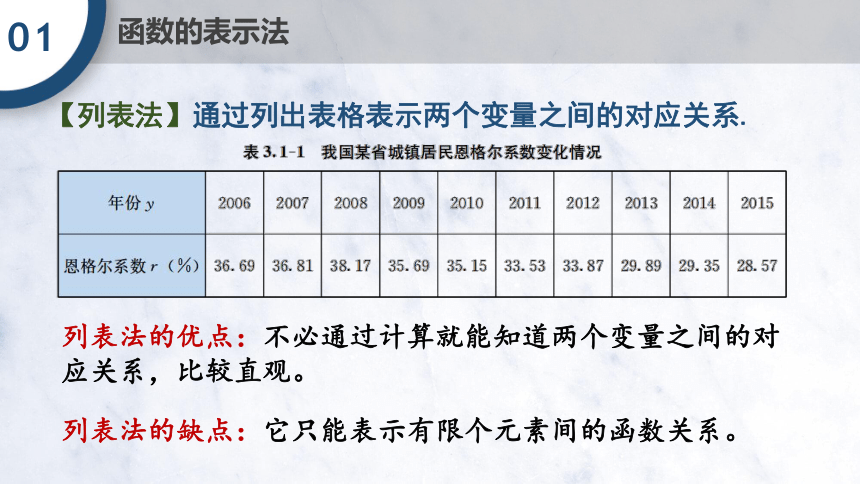
列表法的优点:不必通过计算就能知道两个变量之间的对应关系,比较直观。
列表法的缺点:它只能表示有限个元素间的函数关系。
【列表法】通过列出表格表示两个变量之间的对应关系.
01
函数的表示法
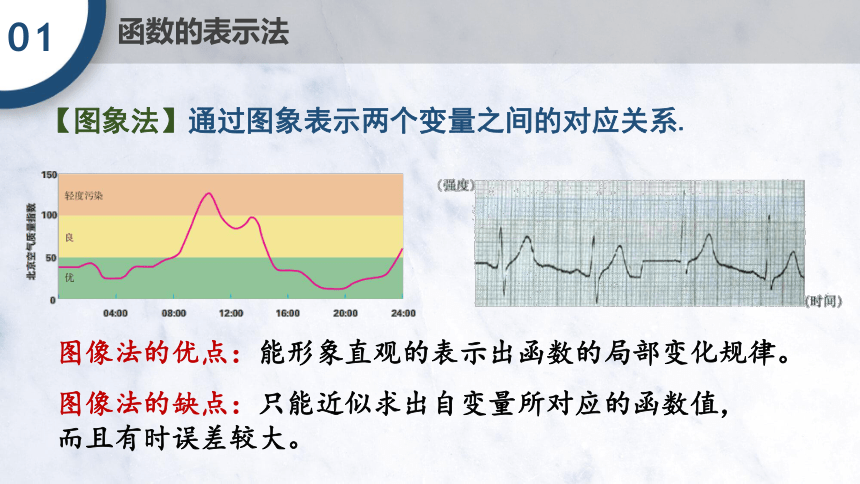
图像法的优点:能形象直观的表示出函数的局部变化规律。
图像法的缺点:只能近似求出自变量所对应的函数值,而且有时误差较大。
【图象法】通过图象表示两个变量之间的对应关系.
01
函数的表示法
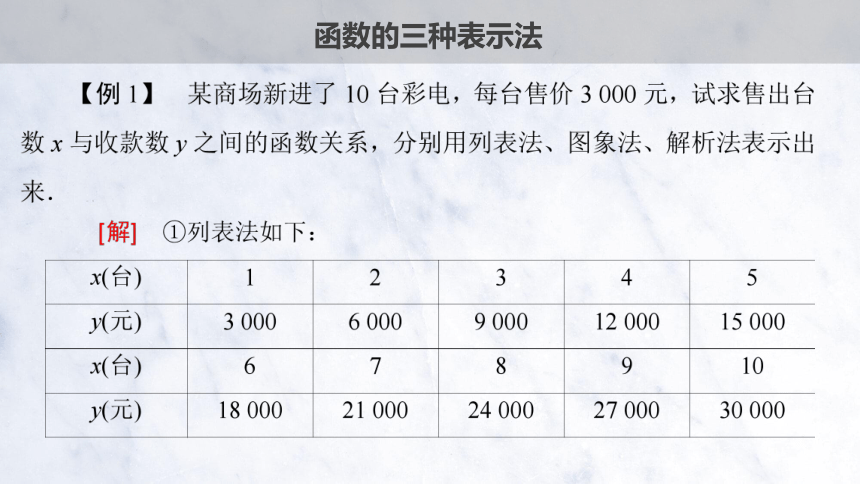
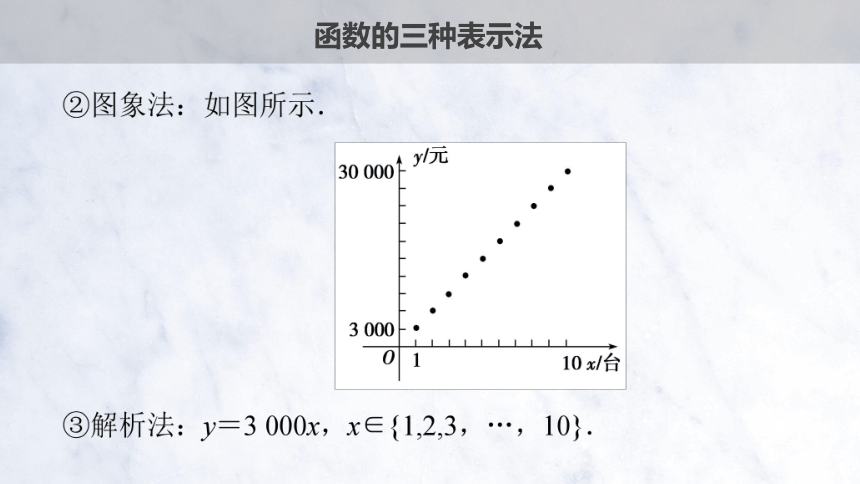
函数的三种表示法
函数的三种表示法
一、配凑法(整体代换法)
02
求解函数解析式
例1 已知函数 f (x+1)=5x-3,求 f (x).
练习 已知函数 f (x-1)=3x+2,求 f (x).
二、换元法
02
求解函数解析式
练习 已知函数 f (x-1)=3x+2,求 f (x).
②
④
③
①
例3 已知f (x)是一次函数,且满足3 f (x+1) - f (x)=2x+9,求 f (x).
三、待定系数法
02
求解函数解析式
练习 已知f (x)是一次函数,且满足f(f (x)) =4x+8,求 f (x).
例4 已知2 f (-x)+ f (x)=x,求 f (x).
四、方程组法
02
求解函数解析式
练习 已知函数f (x)对于任意x的都有 f (x)- 2f (-x)=1+2x,求 f (x).
函数图像为
解: 由绝对值的定义,得:
例5 请画出函数 的图像:
分段函数
同一个函数在不同的范围内有不同的对应法则
03
分段函数
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集。
注:
函数图象既可以是连续的曲线,也可以是直线、线段、折线、离散的点等等。
【分段函数】在定义域的不同部分,有不同的对应法则
03
分段函数
B
例2 给定函数 f (x)=x+1, g(x)=(x+1)2, x∈R.
(1)在同一直角坐标系中画出函数f (x), g(x)的图像;
(2) x∈R,用M(x)表示f (x), g(x)中的较大者,记为
M(x)=max{f (x), g(x)} .
例如当x=2时,M(2)=max{f (2),g (2)}=max{3,9}=9.
请分别用图象法和解析式法表示函数M(x).
在同一坐标系中的f (x), g(x)
M(x)的函数图像:
M(x)的函数解析式:
3.1.2
必修第一册
函数的表示法
XXX学校 XXX
2023.09
00
回顾
函数的表示方法通常有 种,它们是 ____________ 、____________和_____________.
列表法
图像法
解析法
三
【解析法】通过数学表达式表示两个变量之间的对应关系.
正比例函数
反比例函数
一次函数
二次函数
解析法的优点:简明概括了变量间的关系,通过解析式求任意一个函数值
解析法的缺点:并不是所有函数都有解析式。
函数解析式
列表法的优点:不必通过计算就能知道两个变量之间的对应关系,比较直观。
列表法的缺点:它只能表示有限个元素间的函数关系。
【列表法】通过列出表格表示两个变量之间的对应关系.
01
函数的表示法
图像法的优点:能形象直观的表示出函数的局部变化规律。
图像法的缺点:只能近似求出自变量所对应的函数值,而且有时误差较大。
【图象法】通过图象表示两个变量之间的对应关系.
01
函数的表示法
函数的三种表示法
函数的三种表示法
一、配凑法(整体代换法)
02
求解函数解析式
例1 已知函数 f (x+1)=5x-3,求 f (x).
练习 已知函数 f (x-1)=3x+2,求 f (x).
二、换元法
02
求解函数解析式
练习 已知函数 f (x-1)=3x+2,求 f (x).
②
④
③
①
例3 已知f (x)是一次函数,且满足3 f (x+1) - f (x)=2x+9,求 f (x).
三、待定系数法
02
求解函数解析式
练习 已知f (x)是一次函数,且满足f(f (x)) =4x+8,求 f (x).
例4 已知2 f (-x)+ f (x)=x,求 f (x).
四、方程组法
02
求解函数解析式
练习 已知函数f (x)对于任意x的都有 f (x)- 2f (-x)=1+2x,求 f (x).
函数图像为
解: 由绝对值的定义,得:
例5 请画出函数 的图像:
分段函数
同一个函数在不同的范围内有不同的对应法则
03
分段函数
(1)分段函数是一个函数,不要把它误认为是几个函数;
(2)分段函数的定义域是各段定义域的并集,值域是各段值域的并集。
注:
函数图象既可以是连续的曲线,也可以是直线、线段、折线、离散的点等等。
【分段函数】在定义域的不同部分,有不同的对应法则
03
分段函数
B
例2 给定函数 f (x)=x+1, g(x)=(x+1)2, x∈R.
(1)在同一直角坐标系中画出函数f (x), g(x)的图像;
(2) x∈R,用M(x)表示f (x), g(x)中的较大者,记为
M(x)=max{f (x), g(x)} .
例如当x=2时,M(2)=max{f (2),g (2)}=max{3,9}=9.
请分别用图象法和解析式法表示函数M(x).
在同一坐标系中的f (x), g(x)
M(x)的函数图像:
M(x)的函数解析式:
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
