2022-2023学年安徽省皖东名校联盟高二下学期期末监测数学试题(含解析)
文档属性
| 名称 | 2022-2023学年安徽省皖东名校联盟高二下学期期末监测数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 368.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 17:07:30 | ||
图片预览


文档简介
2022-2023学年皖东名校联盟高二期末监测数学试题
第I卷(选择题)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 若,若,则( )
A. B. C. D.
2. 已知等比数列是递增数列,是该数列的前项和,若,是方程的两根,则( )
A. B. C. 或 D. 或
3. 已知圆与圆相交所得的公共弦长为,则圆的半径( )
A. B. C. D.
4. 在平面直角坐标系中,已知顶点和,顶点在椭圆上,则( )
A. B. C. D.
5. 等差数列的前项和为,若,,则当取得最小值时,( )
A. B. C. D.
6. 已知,分别为轴,轴上的动点,若以为直径的圆与直线 相切,则该圆面积的最小值为( )
A. B. C. D.
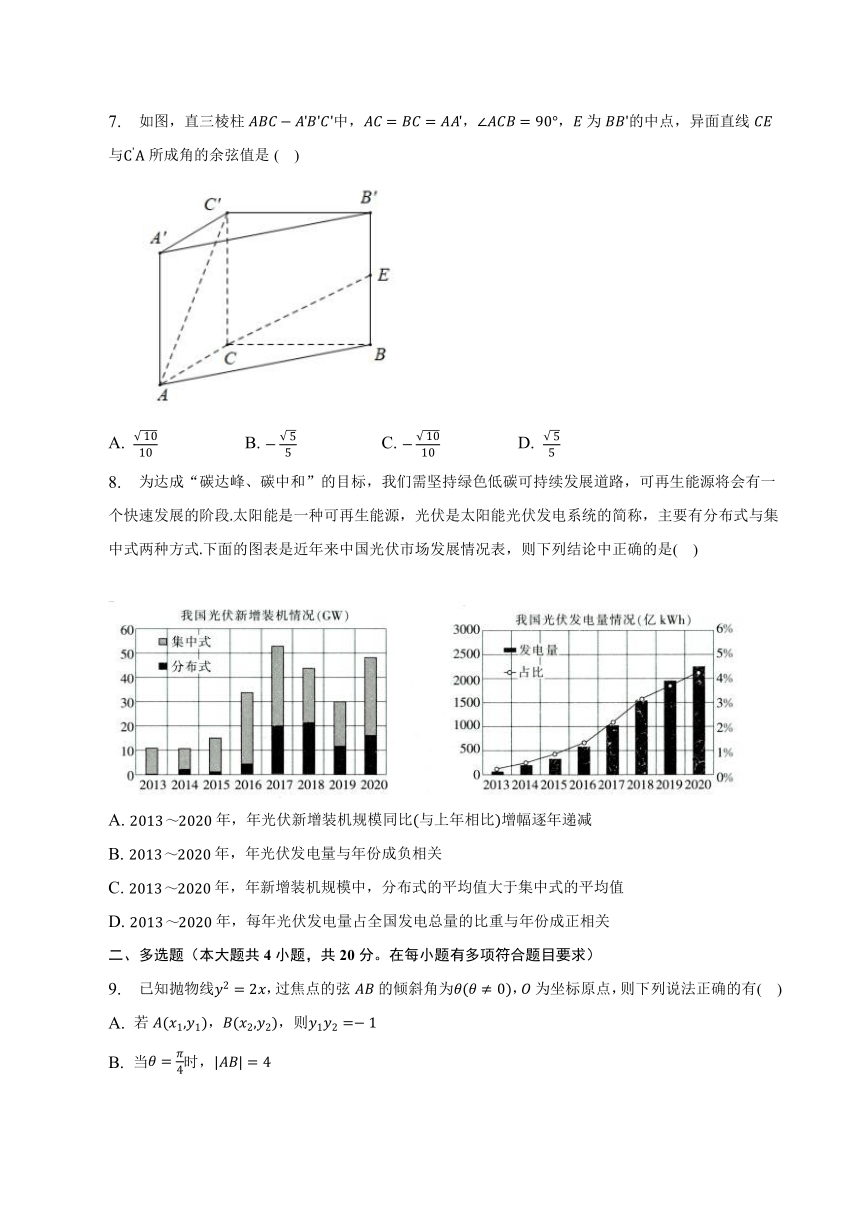
7. 如图,直三棱柱中,,,为的中点,异面直线与所成角的余弦值是( )
A. B. C. D.
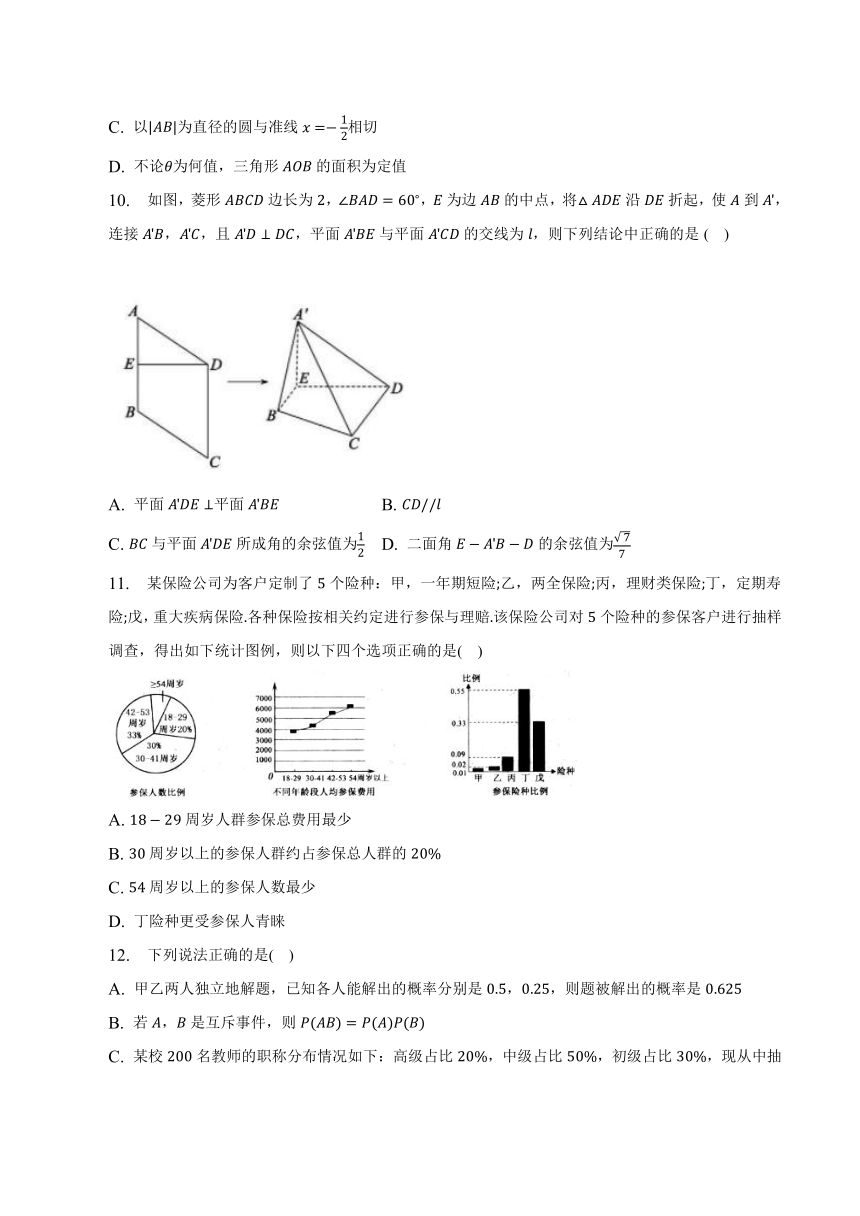
8. 为达成“碳达峰、碳中和”的目标,我们需坚持绿色低碳可持续发展道路,可再生能源将会有一个快速发展的阶段太阳能是一种可再生能源,光伏是太阳能光伏发电系统的简称,主要有分布式与集中式两种方式下面的图表是近年来中国光伏市场发展情况表,则下列结论中正确的是( )
A. 年,年光伏新增装机规模同比与上年相比增幅逐年递减
B. 年,年光伏发电量与年份成负相关
C. 年,年新增装机规模中,分布式的平均值大于集中式的平均值
D. 年,每年光伏发电量占全国发电总量的比重与年份成正相关
二、多选题(本大题共4小题,共20分。在每小题有多项符合题目要求)
9. 已知抛物线,过焦点的弦的倾斜角为,为坐标原点,则下列说法正确的有( )
A. 若,,则
B. 当时,
C. 以为直径的圆与准线相切
D. 不论为何值,三角形的面积为定值
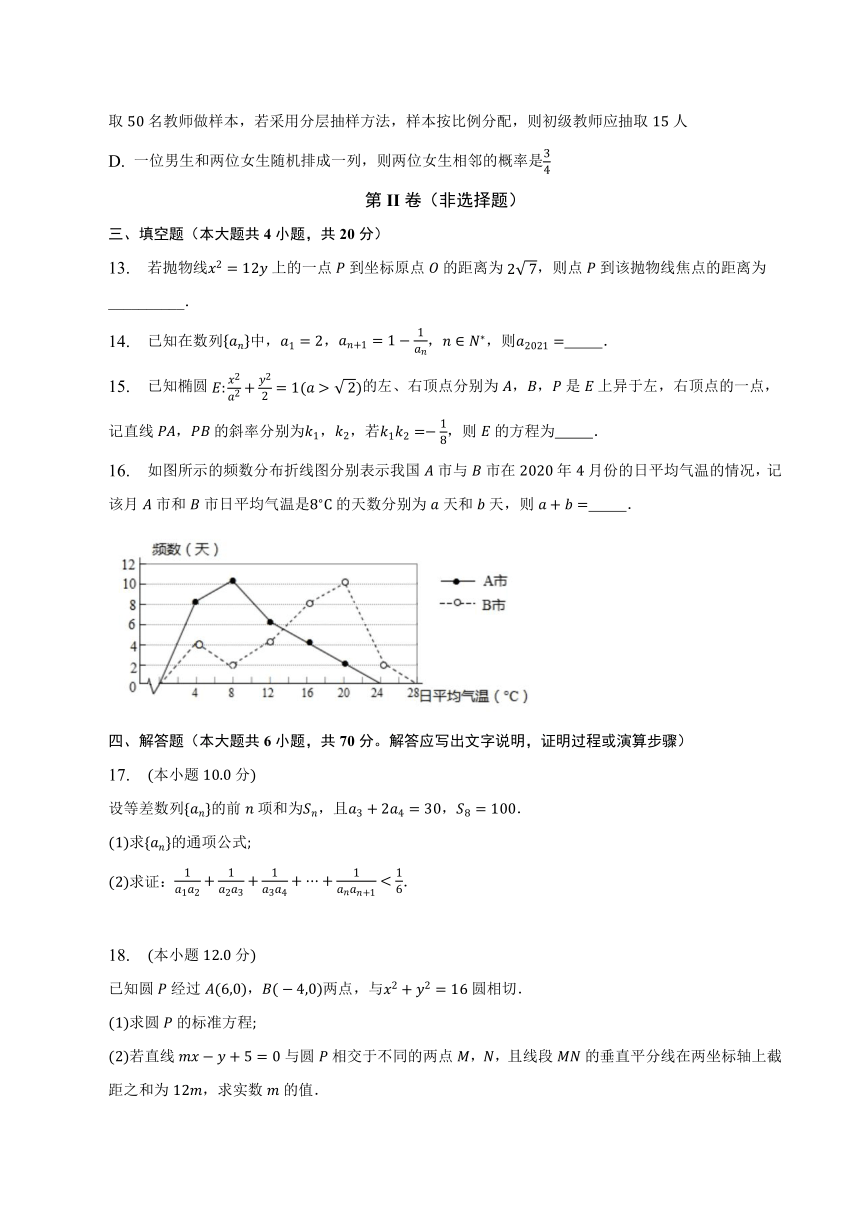
10. 如图,菱形边长为,,为边的中点,将沿折起,使到,连接,,且,平面与平面的交线为,则下列结论中正确的是( )
A. 平面平面 B.
C. 与平面所成角的余弦值为 D. 二面角的余弦值为
11. 某保险公司为客户定制了个险种:甲,一年期短险乙,两全保险丙,理财类保险丁,定期寿险戊,重大疾病保险各种保险按相关约定进行参保与理赔该保险公司对个险种的参保客户进行抽样调查,得出如下统计图例,则以下四个选项正确的是( )
A. 周岁人群参保总费用最少
B. 周岁以上的参保人群约占参保总人群的
C. 周岁以上的参保人数最少
D. 丁险种更受参保人青睐
12. 下列说法正确的是( )
A. 甲乙两人独立地解题,已知各人能解出的概率分别是,,则题被解出的概率是
B. 若,是互斥事件,则
C. 某校名教师的职称分布情况如下:高级占比,中级占比,初级占比,现从中抽取名教师做样本,若采用分层抽样方法,样本按比例分配,则初级教师应抽取人
D. 一位男生和两位女生随机排成一列,则两位女生相邻的概率是
第II卷(非选择题)
三、填空题(本大题共4小题,共20分)
13. 若抛物线上的一点到坐标原点的距离为,则点到该抛物线焦点的距离为__________.
14. 已知在数列中,,,,则 .
15. 已知椭圆的左、右顶点分别为,,是上异于左,右顶点的一点,记直线,的斜率分别为,,若,则的方程为 .
16. 如图所示的频数分布折线图分别表示我国市与市在年月份的日平均气温的情况,记该月市和市日平均气温是的天数分别为天和天,则 .
四、解答题(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
设等差数列的前项和为,且,.
求的通项公式
求证:.
18. 本小题分
已知圆经过,两点,与圆相切.
求圆的标准方程
若直线与圆相交于不同的两点,,且线段的垂直平分线在两坐标轴上截距之和为,求实数的值.
19. 本小题分
今年上海疫情牵动人心,大量医务人员驰援上海现从这些医务人员中随机选取了年龄单位:岁在内的男、女医务人员各人,以他们的年龄作为样本,得出女医务人员的年龄频率分布直方图和男医务人员的年龄频数分布表如下:
年龄单位:岁 频数
求频率分布直方图中的值
根据频率分布直方图估计样本中女医务人员年龄的中位数精确到整数
在上述样本中用分层抽样的方法从年龄在内的女医务人员中抽取人,从年龄在内的男医务人员中抽取人记这人中年龄在内的医务人员有人,再从这人中随机抽取人,求这人是异性的概率.
20. 本小题分
如图,在三棱锥中,为等腰直角三角形,,,为正三角形,为的中点.
证明:平面平面
Ⅱ若二面角的平面角为锐角,且三棱锥的体积为,求直线与平面所成角的正弦值.
21. 本小题分
在平面内,动点与定点的距离和它到定直线:的距离比是常数.
Ⅰ求动点的轨迹方程;
Ⅱ若直线与动点的轨迹交于,两点,且为坐标原点,求的最小值.
22. 本小题分
已知椭圆的右焦点为,点在椭圆上且.
求椭圆的方程;
点分别在椭圆和直线上,为坐标原点,,为的中点,若为直线与直线的交点.是否存在一个确定的曲线,使得始终在该曲线上?若存在,求出该曲线的轨迹方程;若不存在,请说明理由.
答案和解析
1.
【解析】
【分析】
本题考查空间向量平行的坐标运算,属于基础题.
利用空间向量平行的充要条件,列出方程求解的值即可.
【解答】
解:因为,又,,
所以,
则,
得,解得,.
故选D.
2.
【解析】
【分析】
本题考查了等比数列的通项公式与前项和公式,属于基础题.
求出方程的根,结合等比数列的通项公式求出,然后由前项和公式求解即可.
【解答】
解:等比数列是递增数列,,是方程的两根,
,,
,或舍去,
.
故选:.
3.
【解析】
【分析】
本题主要考查相交弦的直线方程,半弦、弦心距和半径间的勾股关系,属于中档题.
两圆方程作差,求出相交弦所在直线方程,再利用半弦、弦心距和半径间的勾股关系建立方程,求出,即可求出半径.
【解答】
解:与两式相减得,即公共弦所在直线方程,圆方程可化为,可得圆心,,圆心到的距离为,半弦长为,则有,解得或舍,此时故选:.
4.
【解析】
【分析】
本题考查椭圆的定义、正弦定理的应用,属于基础题.
先求出,,由正弦定理得答案.
【解答】
解:由椭圆,得,
则和为椭圆的两个焦点.
在椭圆上,
,.
由正弦定理得
.
故选D.
5.
【解析】
【分析】
本题考查了等差数列的性质和前项和,属于基础题.
关键是找出从第几项开始为正值,由题意可得,即可求解.
【解答】
解:,,
所以,,
所以,
所以当时,取得最小值.
故选C.
6.
【解析】
【分析】
本题考查直线与圆的位置关系,注意分析圆面积最小的条件,属于中档题.
根据题意,的中点即圆心,设的中点为,分析可得,过点作直线的垂直线段,交于,交直线于,则当恰为中点时,圆的半径最小,即面积最小,计算可得答案.
【解答】
解:根据题意,圆以为直径,则的中点即圆心,设的中点为,圆半径为,
由已知得,
过点作直线的垂直线段,
交于,交直线于,
则当恰为中点时,圆的半径最小,即面积最小.
此时圆的直径为到直线的距离:
此时圆的半径,
则圆的面积的最小值.
故选C.
7.
【解析】
【分析】
本题考查由空间向量夹角公式求异面直线所成角,属中档题.
设,由已知,用表示与,再利用向量夹角公式求即可.
【解答】
解:由题意设,
,
,
,
,
即异面直线与所成角的余弦值为.
故选A.
8.
【解析】解:,年,年光伏新增装机规模同比与上年相比增幅逐年递减,前几年递增,后面递减,故A错误;
,年,年光伏发电量与年份成正相关,故B错误;
,由图表可以看出,每一年装机规模,集中式都比分布式大,因此分布式的平均值小于集中式的平均值,故C错误;
,根据图表可知,年,每年光伏发电量占全国发电总量的比重随年份逐年增加,
故每年光伏发电量占全国发电总量的比重与年份成正相关,故D正确.
故选:.
根据条形图中的数据逐一分析即可得出结果.
本题考查了条形图的应用,读懂统计图并能从统计图得到必要的信息是解决问题的关键,属于基础题.
9.
【解析】
【分析】
本题考查抛物线的性质和方程,考查三角形面积的求法,属于基础题.
设直线的方程为,根据根与系数的关系和抛物线的性质,以及三角形的面积公式即可判断.
【解答】
解:设直线的方程为,
联立方程组,消可得,,
,,
,故A正确;
当时,此时直线方程为,
联立方程组,消整理可得,
,
,故B正确;
由可得,,
,
以为直径的圆的圆心坐标为,
则圆心到直线的距离为,故C正确;
设原点到直线的距离,
,不是定值.故D不正确.
故选ABC.
10.
【解析】
【分析】
本题考查二面角,直线和平面所成的角,面面垂直的判定,线面平行的判定与性质,属于较难题.
将沿折起,使点到点,根据面面垂直的判定定理推导平面平面,可判断选项A;根据线面平行的性质定理推导,可判断选项B;取中点为,连接,则可得与平面所成的角,即为与平面所成的角,即为,解三角形即可得解判断;取中点,证得即为二面角的平面角,解三角形即可得解判断.
【解答】
解:对于,菱形的边长为,,点为的中点,则,,
将沿折起,使点到点,且,
又,、平面,所以平面,
又,所以平面,
又平面,所以平面平面,故A正确;
对于,因为,又平面,平面,
所以平面,又平面,平面平面,所以,故B正确;
对于,取中点为,连接,
易知,则四边形为平行四边形,
故EF,又平面,
故BC与平面所成的角,即为与平面所成的角,即为,
中,,,,
故,故C错误;
对于,取的中点,连接,,,
由前面的分析可知平面,平面,
又平面,故BE,
又,故为等腰直角三角形,,
又为中点,故,
中,,,,
又为中点,故,
故即为二面角的平面角,
中,,,,
,故,
故,故D正确.
11.
【解析】
【分析】
本题考查了数据分析的应用,应用了饼状图、折线图及柱状图,属于基础题.
由饼状图及折线图判断选项A,由饼状图判断选项B、,由柱状图判断选项D即可.
【解答】
解:对于选项A,由饼状图及折线图可知,
,
故周岁人群参保总费用最少,故正确;
对于选项B,由饼状图可知,
周岁以上的参保人群约占参保人群的,故错误;
对于选项C,由饼状图可知,
周岁以上的参保人数约占,人数最小,故正确;
对于选项D,由柱状图可知,
丁险种更受参保人青睐,故正确;
故选:.
12.
【解析】
【分析】
本题考查了相互独立事件同时发生的概率、互斥事件与对立事件、分层随机抽样、排列与排列数以及古典概型,属于中档题.
对于,正难则反,先计算题没被解出的概率,再根据对立事件计算题被解出的概率;对于,由互斥事件的定义立得;对于,根据分层抽样的性质可得;对于,先计算人排成一排所有的排法数,再计算女生不相邻的排法数,根据古典概型计算出女生不相邻的概率,再由对立事件计算出女生相邻的概率.
【解答】
解:题没被解出的概率为,故题被解出的概率为,故选项A正确;
B. , 是互斥事件,则事件,同时发生的概率为,故选项B错误;
C.根据分层随机抽样,由知高级教师应抽取人,故选项C正确;
D.设男生为甲,女生为乙和丙,则将这人排成一排,共有种排法,其中女生不相邻有:乙,甲,丙,丙,甲,乙种排法,由古典概型得女生不相邻的概率为,故女生相邻的概率为,故选项D错误.
13.
【解析】
【分析】
本题考查两点间的距离公式,抛物线的定义与焦点、准线 ,考查转化思想与方程思想,属于基础题.
求得点的坐标,将点到该抛物线焦点的距离转化为点到抛物线准线的距离即可求解.
【解答】
解:设点,
,
,
解得 或舍去,则点的纵坐标为,
抛物线,其准线方程为,
到抛物线的焦点的距离与到准线的距离相等,
点到该抛物线焦点的距离为.
故答案为:.
14.
【解析】
【分析】
本题考查根据数列递推关系求数列的项,数列的周期性,属于基础题.
由递推关系依次求出数列的前几项,归纳出周期后可得结论.
【解答】
解:由题意,,,,
所以数列是周期数列,且周期为,所以.
故答案为:.
15.
【解析】
【分析】
本题考查了椭圆的标准方程,过两点的斜率公式,是中档题.
设,计算,得出,可得椭圆方程.
【解答】
解:设,所以,即,
所以,,
所以
,解得,
所以的方程为.
故答案为.
16.
【解析】
【分析】
本题考查了频数分布折线统计图,属于基础题.
观察频数分布折线图获得、的值,即可求解.
【解答】
解:由频数分布折线图看出市日平均气温是的天数为天,
市日平均气温是的天数为天,
即,,
所以.
故答案为:.
17.解:设等差数列的公差为,因为,,
所以
解得,,
所以,
证明:
,
又,所以,所以,
故.
【解析】本题考查等差数列的通项公式与前项和公式,及裂项相消法求和的应用,属于中档题.
由题意求得,,可求等差数列的通项公式;
由裂项相消法求和化简,即可证明.
18.解:设圆的方程为,
因为圆经过,两点,与圆相切,
所以,解得
所以圆的标准方程为:
若,直线为,与圆相切,只有一个交点,不合题意,故
又弦的垂直平分线必过圆心,且的斜率为,
所以线段的垂直平分线方程为,
当时,,当时,,所以,即,
解得:或
因为圆的方程为:,所以,半径,
又直线与圆相交,所以圆心到直线的距离,即,
得或,
符合题意,即.
【解析】本题主要考查圆的标准方程和直线与圆的位置关系的应用,注意对进行分类讨论,属于中档题.
19.解:解:由题意,,解得:;
设中位数为,则有,
故,
即中位数估计为;
解:由已知得名女医务人员中,
年龄在内的有人,
在内的有人,
名男医务人员中,年龄在内的有人,
在内的有人,
这人中,年龄在内的有人,其中女医务人员有人,
记为,,男医务人员有人,记为,,
设从这人中抽取人,这人是异性为事件,则样本空间为
,,,,,,,,,,共种情况;
,,,,,,包含个样本点,
故.
【解析】本题考查了频率分布直方图,也考查了古典概型的概率计算问题,属于中档题.
根据频率分布直方图的条形图的面积和为计算即可;
根据中位数的计算方法即可求解;
根据古典概型的概率计算方法,列出样本空间和满足条件的样本点,再由古典概型的概率公式计算即可.
20.Ⅰ证明:,为中点,.
又为等边三角形,,.
,,平面,
平面.
又平面,
平面平面.
Ⅱ由Ⅰ知点在平面内的射影在直线上,又二面角的平面角为锐角,
在射线上,,,
,
又,
,
即为中点,取中点,连接,则,
平面,,,两两互相垂直
以为坐标原点,,,所在直线分别为轴,轴,轴建立空间直角坐标系
则,,,,
,.
设平面的法向量为
由得
令,得平面的一个法向量为,
又,设与平面所成角为,
则.
直线与平面所成角的正弦值为.
【解析】本题考查面面垂直的判定及线面角,二面角的求法,属于中档题.
Ⅰ证出平面,结合面面垂直的判定定理即可证明;
Ⅱ设在面内的射影为,由三棱锥的体积求得,得到为中点,取中点,连接,证得,,两两互相垂直,建立空间坐标系,求得平面的法向量为及,代入公式即可求解.
21. 解:Ⅰ由已知可得:,
整理化简可得:,即,
所以动点的轨迹方程为;
Ⅱ易知直线与直线的斜率均存在,
由,可设直线的方程为,直线的方程为,
由,可得
所以,
同理可得,
又由且,可得,
所以,
所以
,
当且仅当,即时等号成立,
当时,,解得,满足题意,
所以的最小值为.
【解析】本题考查圆锥曲线中的轨迹问题、直线与双曲线的位置关系、利用基本不等式求最值,属于中档题.
Ⅰ根据题意得出,化简即可求出结果;
Ⅱ易知直线与直线的斜率均存在,由可设直线的方程为,直线的方程为,与双曲线方程联立,求出,
,即可得出,求出,再利用基本不等式即可求出结果.
22.解:因为椭圆过点,所以.
因为,所以,得.
故,
所以椭圆的方程为.
设,则直线的斜率为.
因为,所以直线的方程为.
令可得,所以,
又是的中点,所以.
从而,,
所以,
因为点在椭圆上,所以,故,
代入式可得,所以,
所以点始终在以为直径的圆上,
圆心为中点,半径,
所以该圆方程为.
故存在一个确定的曲线,使得始终在该曲线上,该曲线的轨迹方程为.
【解析】本题考查了椭圆的标准方程,直线与椭圆的位置关系及其应用,考查了运算推理能力,属于较难题.
利用待定系数法求出椭圆的方程;
设,表示出直线的方程,求出点和,进而求出,把代入得,从而,判断出点始终在以为直径的圆上,即可求解.
第I卷(选择题)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 若,若,则( )
A. B. C. D.
2. 已知等比数列是递增数列,是该数列的前项和,若,是方程的两根,则( )
A. B. C. 或 D. 或
3. 已知圆与圆相交所得的公共弦长为,则圆的半径( )
A. B. C. D.
4. 在平面直角坐标系中,已知顶点和,顶点在椭圆上,则( )
A. B. C. D.
5. 等差数列的前项和为,若,,则当取得最小值时,( )
A. B. C. D.
6. 已知,分别为轴,轴上的动点,若以为直径的圆与直线 相切,则该圆面积的最小值为( )
A. B. C. D.
7. 如图,直三棱柱中,,,为的中点,异面直线与所成角的余弦值是( )
A. B. C. D.
8. 为达成“碳达峰、碳中和”的目标,我们需坚持绿色低碳可持续发展道路,可再生能源将会有一个快速发展的阶段太阳能是一种可再生能源,光伏是太阳能光伏发电系统的简称,主要有分布式与集中式两种方式下面的图表是近年来中国光伏市场发展情况表,则下列结论中正确的是( )
A. 年,年光伏新增装机规模同比与上年相比增幅逐年递减
B. 年,年光伏发电量与年份成负相关
C. 年,年新增装机规模中,分布式的平均值大于集中式的平均值
D. 年,每年光伏发电量占全国发电总量的比重与年份成正相关
二、多选题(本大题共4小题,共20分。在每小题有多项符合题目要求)
9. 已知抛物线,过焦点的弦的倾斜角为,为坐标原点,则下列说法正确的有( )
A. 若,,则
B. 当时,
C. 以为直径的圆与准线相切
D. 不论为何值,三角形的面积为定值
10. 如图,菱形边长为,,为边的中点,将沿折起,使到,连接,,且,平面与平面的交线为,则下列结论中正确的是( )
A. 平面平面 B.
C. 与平面所成角的余弦值为 D. 二面角的余弦值为
11. 某保险公司为客户定制了个险种:甲,一年期短险乙,两全保险丙,理财类保险丁,定期寿险戊,重大疾病保险各种保险按相关约定进行参保与理赔该保险公司对个险种的参保客户进行抽样调查,得出如下统计图例,则以下四个选项正确的是( )
A. 周岁人群参保总费用最少
B. 周岁以上的参保人群约占参保总人群的
C. 周岁以上的参保人数最少
D. 丁险种更受参保人青睐
12. 下列说法正确的是( )
A. 甲乙两人独立地解题,已知各人能解出的概率分别是,,则题被解出的概率是
B. 若,是互斥事件,则
C. 某校名教师的职称分布情况如下:高级占比,中级占比,初级占比,现从中抽取名教师做样本,若采用分层抽样方法,样本按比例分配,则初级教师应抽取人
D. 一位男生和两位女生随机排成一列,则两位女生相邻的概率是
第II卷(非选择题)
三、填空题(本大题共4小题,共20分)
13. 若抛物线上的一点到坐标原点的距离为,则点到该抛物线焦点的距离为__________.
14. 已知在数列中,,,,则 .
15. 已知椭圆的左、右顶点分别为,,是上异于左,右顶点的一点,记直线,的斜率分别为,,若,则的方程为 .
16. 如图所示的频数分布折线图分别表示我国市与市在年月份的日平均气温的情况,记该月市和市日平均气温是的天数分别为天和天,则 .
四、解答题(本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
设等差数列的前项和为,且,.
求的通项公式
求证:.
18. 本小题分
已知圆经过,两点,与圆相切.
求圆的标准方程
若直线与圆相交于不同的两点,,且线段的垂直平分线在两坐标轴上截距之和为,求实数的值.
19. 本小题分
今年上海疫情牵动人心,大量医务人员驰援上海现从这些医务人员中随机选取了年龄单位:岁在内的男、女医务人员各人,以他们的年龄作为样本,得出女医务人员的年龄频率分布直方图和男医务人员的年龄频数分布表如下:
年龄单位:岁 频数
求频率分布直方图中的值
根据频率分布直方图估计样本中女医务人员年龄的中位数精确到整数
在上述样本中用分层抽样的方法从年龄在内的女医务人员中抽取人,从年龄在内的男医务人员中抽取人记这人中年龄在内的医务人员有人,再从这人中随机抽取人,求这人是异性的概率.
20. 本小题分
如图,在三棱锥中,为等腰直角三角形,,,为正三角形,为的中点.
证明:平面平面
Ⅱ若二面角的平面角为锐角,且三棱锥的体积为,求直线与平面所成角的正弦值.
21. 本小题分
在平面内,动点与定点的距离和它到定直线:的距离比是常数.
Ⅰ求动点的轨迹方程;
Ⅱ若直线与动点的轨迹交于,两点,且为坐标原点,求的最小值.
22. 本小题分
已知椭圆的右焦点为,点在椭圆上且.
求椭圆的方程;
点分别在椭圆和直线上,为坐标原点,,为的中点,若为直线与直线的交点.是否存在一个确定的曲线,使得始终在该曲线上?若存在,求出该曲线的轨迹方程;若不存在,请说明理由.
答案和解析
1.
【解析】
【分析】
本题考查空间向量平行的坐标运算,属于基础题.
利用空间向量平行的充要条件,列出方程求解的值即可.
【解答】
解:因为,又,,
所以,
则,
得,解得,.
故选D.
2.
【解析】
【分析】
本题考查了等比数列的通项公式与前项和公式,属于基础题.
求出方程的根,结合等比数列的通项公式求出,然后由前项和公式求解即可.
【解答】
解:等比数列是递增数列,,是方程的两根,
,,
,或舍去,
.
故选:.
3.
【解析】
【分析】
本题主要考查相交弦的直线方程,半弦、弦心距和半径间的勾股关系,属于中档题.
两圆方程作差,求出相交弦所在直线方程,再利用半弦、弦心距和半径间的勾股关系建立方程,求出,即可求出半径.
【解答】
解:与两式相减得,即公共弦所在直线方程,圆方程可化为,可得圆心,,圆心到的距离为,半弦长为,则有,解得或舍,此时故选:.
4.
【解析】
【分析】
本题考查椭圆的定义、正弦定理的应用,属于基础题.
先求出,,由正弦定理得答案.
【解答】
解:由椭圆,得,
则和为椭圆的两个焦点.
在椭圆上,
,.
由正弦定理得
.
故选D.
5.
【解析】
【分析】
本题考查了等差数列的性质和前项和,属于基础题.
关键是找出从第几项开始为正值,由题意可得,即可求解.
【解答】
解:,,
所以,,
所以,
所以当时,取得最小值.
故选C.
6.
【解析】
【分析】
本题考查直线与圆的位置关系,注意分析圆面积最小的条件,属于中档题.
根据题意,的中点即圆心,设的中点为,分析可得,过点作直线的垂直线段,交于,交直线于,则当恰为中点时,圆的半径最小,即面积最小,计算可得答案.
【解答】
解:根据题意,圆以为直径,则的中点即圆心,设的中点为,圆半径为,
由已知得,
过点作直线的垂直线段,
交于,交直线于,
则当恰为中点时,圆的半径最小,即面积最小.
此时圆的直径为到直线的距离:
此时圆的半径,
则圆的面积的最小值.
故选C.
7.
【解析】
【分析】
本题考查由空间向量夹角公式求异面直线所成角,属中档题.
设,由已知,用表示与,再利用向量夹角公式求即可.
【解答】
解:由题意设,
,
,
,
,
即异面直线与所成角的余弦值为.
故选A.
8.
【解析】解:,年,年光伏新增装机规模同比与上年相比增幅逐年递减,前几年递增,后面递减,故A错误;
,年,年光伏发电量与年份成正相关,故B错误;
,由图表可以看出,每一年装机规模,集中式都比分布式大,因此分布式的平均值小于集中式的平均值,故C错误;
,根据图表可知,年,每年光伏发电量占全国发电总量的比重随年份逐年增加,
故每年光伏发电量占全国发电总量的比重与年份成正相关,故D正确.
故选:.
根据条形图中的数据逐一分析即可得出结果.
本题考查了条形图的应用,读懂统计图并能从统计图得到必要的信息是解决问题的关键,属于基础题.
9.
【解析】
【分析】
本题考查抛物线的性质和方程,考查三角形面积的求法,属于基础题.
设直线的方程为,根据根与系数的关系和抛物线的性质,以及三角形的面积公式即可判断.
【解答】
解:设直线的方程为,
联立方程组,消可得,,
,,
,故A正确;
当时,此时直线方程为,
联立方程组,消整理可得,
,
,故B正确;
由可得,,
,
以为直径的圆的圆心坐标为,
则圆心到直线的距离为,故C正确;
设原点到直线的距离,
,不是定值.故D不正确.
故选ABC.
10.
【解析】
【分析】
本题考查二面角,直线和平面所成的角,面面垂直的判定,线面平行的判定与性质,属于较难题.
将沿折起,使点到点,根据面面垂直的判定定理推导平面平面,可判断选项A;根据线面平行的性质定理推导,可判断选项B;取中点为,连接,则可得与平面所成的角,即为与平面所成的角,即为,解三角形即可得解判断;取中点,证得即为二面角的平面角,解三角形即可得解判断.
【解答】
解:对于,菱形的边长为,,点为的中点,则,,
将沿折起,使点到点,且,
又,、平面,所以平面,
又,所以平面,
又平面,所以平面平面,故A正确;
对于,因为,又平面,平面,
所以平面,又平面,平面平面,所以,故B正确;
对于,取中点为,连接,
易知,则四边形为平行四边形,
故EF,又平面,
故BC与平面所成的角,即为与平面所成的角,即为,
中,,,,
故,故C错误;
对于,取的中点,连接,,,
由前面的分析可知平面,平面,
又平面,故BE,
又,故为等腰直角三角形,,
又为中点,故,
中,,,,
又为中点,故,
故即为二面角的平面角,
中,,,,
,故,
故,故D正确.
11.
【解析】
【分析】
本题考查了数据分析的应用,应用了饼状图、折线图及柱状图,属于基础题.
由饼状图及折线图判断选项A,由饼状图判断选项B、,由柱状图判断选项D即可.
【解答】
解:对于选项A,由饼状图及折线图可知,
,
故周岁人群参保总费用最少,故正确;
对于选项B,由饼状图可知,
周岁以上的参保人群约占参保人群的,故错误;
对于选项C,由饼状图可知,
周岁以上的参保人数约占,人数最小,故正确;
对于选项D,由柱状图可知,
丁险种更受参保人青睐,故正确;
故选:.
12.
【解析】
【分析】
本题考查了相互独立事件同时发生的概率、互斥事件与对立事件、分层随机抽样、排列与排列数以及古典概型,属于中档题.
对于,正难则反,先计算题没被解出的概率,再根据对立事件计算题被解出的概率;对于,由互斥事件的定义立得;对于,根据分层抽样的性质可得;对于,先计算人排成一排所有的排法数,再计算女生不相邻的排法数,根据古典概型计算出女生不相邻的概率,再由对立事件计算出女生相邻的概率.
【解答】
解:题没被解出的概率为,故题被解出的概率为,故选项A正确;
B. , 是互斥事件,则事件,同时发生的概率为,故选项B错误;
C.根据分层随机抽样,由知高级教师应抽取人,故选项C正确;
D.设男生为甲,女生为乙和丙,则将这人排成一排,共有种排法,其中女生不相邻有:乙,甲,丙,丙,甲,乙种排法,由古典概型得女生不相邻的概率为,故女生相邻的概率为,故选项D错误.
13.
【解析】
【分析】
本题考查两点间的距离公式,抛物线的定义与焦点、准线 ,考查转化思想与方程思想,属于基础题.
求得点的坐标,将点到该抛物线焦点的距离转化为点到抛物线准线的距离即可求解.
【解答】
解:设点,
,
,
解得 或舍去,则点的纵坐标为,
抛物线,其准线方程为,
到抛物线的焦点的距离与到准线的距离相等,
点到该抛物线焦点的距离为.
故答案为:.
14.
【解析】
【分析】
本题考查根据数列递推关系求数列的项,数列的周期性,属于基础题.
由递推关系依次求出数列的前几项,归纳出周期后可得结论.
【解答】
解:由题意,,,,
所以数列是周期数列,且周期为,所以.
故答案为:.
15.
【解析】
【分析】
本题考查了椭圆的标准方程,过两点的斜率公式,是中档题.
设,计算,得出,可得椭圆方程.
【解答】
解:设,所以,即,
所以,,
所以
,解得,
所以的方程为.
故答案为.
16.
【解析】
【分析】
本题考查了频数分布折线统计图,属于基础题.
观察频数分布折线图获得、的值,即可求解.
【解答】
解:由频数分布折线图看出市日平均气温是的天数为天,
市日平均气温是的天数为天,
即,,
所以.
故答案为:.
17.解:设等差数列的公差为,因为,,
所以
解得,,
所以,
证明:
,
又,所以,所以,
故.
【解析】本题考查等差数列的通项公式与前项和公式,及裂项相消法求和的应用,属于中档题.
由题意求得,,可求等差数列的通项公式;
由裂项相消法求和化简,即可证明.
18.解:设圆的方程为,
因为圆经过,两点,与圆相切,
所以,解得
所以圆的标准方程为:
若,直线为,与圆相切,只有一个交点,不合题意,故
又弦的垂直平分线必过圆心,且的斜率为,
所以线段的垂直平分线方程为,
当时,,当时,,所以,即,
解得:或
因为圆的方程为:,所以,半径,
又直线与圆相交,所以圆心到直线的距离,即,
得或,
符合题意,即.
【解析】本题主要考查圆的标准方程和直线与圆的位置关系的应用,注意对进行分类讨论,属于中档题.
19.解:解:由题意,,解得:;
设中位数为,则有,
故,
即中位数估计为;
解:由已知得名女医务人员中,
年龄在内的有人,
在内的有人,
名男医务人员中,年龄在内的有人,
在内的有人,
这人中,年龄在内的有人,其中女医务人员有人,
记为,,男医务人员有人,记为,,
设从这人中抽取人,这人是异性为事件,则样本空间为
,,,,,,,,,,共种情况;
,,,,,,包含个样本点,
故.
【解析】本题考查了频率分布直方图,也考查了古典概型的概率计算问题,属于中档题.
根据频率分布直方图的条形图的面积和为计算即可;
根据中位数的计算方法即可求解;
根据古典概型的概率计算方法,列出样本空间和满足条件的样本点,再由古典概型的概率公式计算即可.
20.Ⅰ证明:,为中点,.
又为等边三角形,,.
,,平面,
平面.
又平面,
平面平面.
Ⅱ由Ⅰ知点在平面内的射影在直线上,又二面角的平面角为锐角,
在射线上,,,
,
又,
,
即为中点,取中点,连接,则,
平面,,,两两互相垂直
以为坐标原点,,,所在直线分别为轴,轴,轴建立空间直角坐标系
则,,,,
,.
设平面的法向量为
由得
令,得平面的一个法向量为,
又,设与平面所成角为,
则.
直线与平面所成角的正弦值为.
【解析】本题考查面面垂直的判定及线面角,二面角的求法,属于中档题.
Ⅰ证出平面,结合面面垂直的判定定理即可证明;
Ⅱ设在面内的射影为,由三棱锥的体积求得,得到为中点,取中点,连接,证得,,两两互相垂直,建立空间坐标系,求得平面的法向量为及,代入公式即可求解.
21. 解:Ⅰ由已知可得:,
整理化简可得:,即,
所以动点的轨迹方程为;
Ⅱ易知直线与直线的斜率均存在,
由,可设直线的方程为,直线的方程为,
由,可得
所以,
同理可得,
又由且,可得,
所以,
所以
,
当且仅当,即时等号成立,
当时,,解得,满足题意,
所以的最小值为.
【解析】本题考查圆锥曲线中的轨迹问题、直线与双曲线的位置关系、利用基本不等式求最值,属于中档题.
Ⅰ根据题意得出,化简即可求出结果;
Ⅱ易知直线与直线的斜率均存在,由可设直线的方程为,直线的方程为,与双曲线方程联立,求出,
,即可得出,求出,再利用基本不等式即可求出结果.
22.解:因为椭圆过点,所以.
因为,所以,得.
故,
所以椭圆的方程为.
设,则直线的斜率为.
因为,所以直线的方程为.
令可得,所以,
又是的中点,所以.
从而,,
所以,
因为点在椭圆上,所以,故,
代入式可得,所以,
所以点始终在以为直径的圆上,
圆心为中点,半径,
所以该圆方程为.
故存在一个确定的曲线,使得始终在该曲线上,该曲线的轨迹方程为.
【解析】本题考查了椭圆的标准方程,直线与椭圆的位置关系及其应用,考查了运算推理能力,属于较难题.
利用待定系数法求出椭圆的方程;
设,表示出直线的方程,求出点和,进而求出,把代入得,从而,判断出点始终在以为直径的圆上,即可求解.
同课章节目录
