2023-2024学年人教版九年级数学上册 22.3实际问题与二次函数 同步测试卷 (无答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册 22.3实际问题与二次函数 同步测试卷 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 487.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 00:00:00 | ||
图片预览




文档简介
22.3 实际问题与二次函数 同步测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,从地面竖直向上抛出一个小球,小球的高度单位: 与小球运动时间单位:之间的函数关系式为,那么小球从抛出至回落到地面所需的时间是( )
A. B. C. D.
2. 在月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
A. 月份 B. 月份 C. 月份 D. 月份
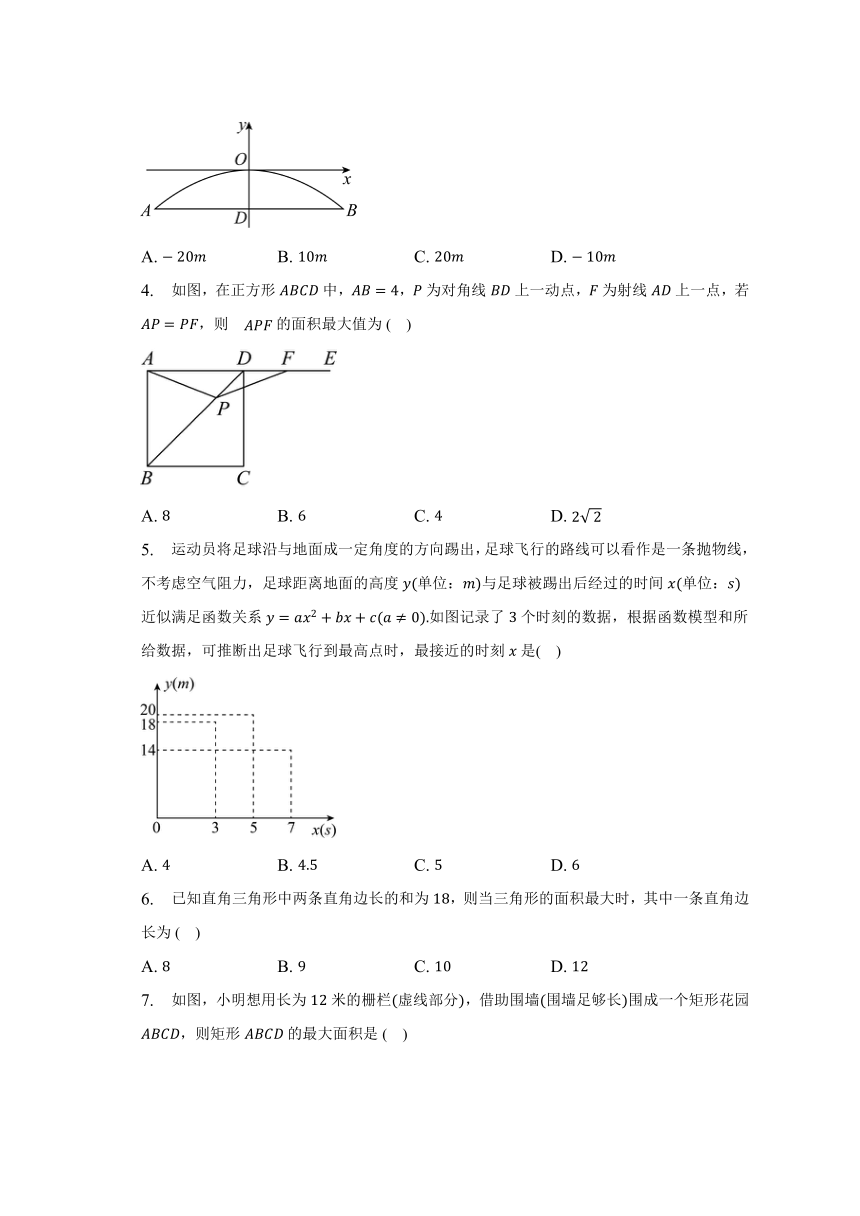
3. 河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为,当水面离桥拱顶的高度是时,这时水面宽度为( )
A. B. C. D.
4. 如图,在正方形中,,为对角线上一动点,为射线上一点,若,则的面积最大值为( )
A. B. C. D.
5. 运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线可以看作是一条抛物线,不考虑空气阻力,足球距离地面的高度单位:与足球被踢出后经过的时间单位:近似满足函数关系如图记录了个时刻的数据,根据函数模型和所给数据,可推断出足球飞行到最高点时,最接近的时刻是( )
A. B. C. D.
6. 已知直角三角形中两条直角边长的和为,则当三角形的面积最大时,其中一条直角边长为( )
A. B. C. D.
7. 如图,小明想用长为米的栅栏虚线部分,借助围墙围墙足够长围成一个矩形花园,则矩形的最大面积是( )
A. 平方米 B. 平方米 C. 平方米 D. 平方米
8. 如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系下列叙述正确的是( )
A. 小球的飞行高度不能达到 B. 小球的飞行高度可以达到
C. 小球从飞出到落地要用时 D. 小球飞出时的飞行高度为
二、填空题(本大题共8小题,共24分)
9. 边长为的正方形在平面直角坐标系中的位置如图所示,点是边的中点,连接,点在第一象限,且,以直线为对称轴的抛物线过,两点.点为直线上一动点,点为抛物线上一动点,当以点,,,为顶点的四边形是平行四边形时点的坐标为 .
10. 斜抛小球,小球触地后呈抛物线反弹,每次反弹后保持保同的抛物线形状开口方向与开口大小前后一致,第一次反弹后的最大高度为,第二次反弹后的最大高度为,第二次反弹后,小球越过最高点落在垂直于地面的挡板处,且离地高度,若,,则为 .
11. 一座拱桥的轮廓是抛物线型如图所示,桥高为米,拱高米,跨度米.相邻两支柱间的距离均为米,则支柱的高度为 米.
12. 如图,矩形中,点是的中点,点是上的任意一点不与,重合连接,以为斜边,构造等腰,点在矩形内部,连接,若,,则的取值范围为 .
13. 音乐喷泉图可以使喷水造型随音乐的节奏起伏变化而变化,某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边,音乐变化时,抛物线的顶点在直线上变动,从而产生一组不同的抛物线图,这组抛物线的统一形式为若要求喷出的抛物线水线不能到岸边,则的取值范围为___ ____.
14. 如图,矩形中,,动点从点出发,以的速度沿向终点移动,设移动时间为连接,以为一边作正方形,连接、,则面积最小值为 .
15. 如图,线段,点是线段上的一个动点,分别以和为边在线段的同侧构造菱形和菱形,且,是菱形的对角线交点、是菱形的对角线交点,连接,则线段的最小值为 .
16. 一种包装盒的设计方法如图所示,是边长为的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得、、、四点重合于图中的点,形成一个底面为正方形的长方体包装盒,要使包装盒的侧面积最大,则应取 .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图,地面上两根等长立柱,之间悬挂一根近似成抛物线的绳子.
求绳子最低点离地面的距离;
因实际需要,在离为米的位置处用一根立柱撑起绳子如图,使左边抛物线的最低点距为米,离地面米,求的长;
将立柱的长度提升为米,通过调整的位置,使抛物线对应函数的二次项系数始终为,设离的距离为,抛物线的顶点离地面距离为,当时,求的取值范围.
18. 本小题分
有一个抛物线的拱形桥洞,桥洞离水面的最大高度为,跨度为,如图所示,把它的图形放在直角坐标系中
求这条抛物线所对应的函数关系式;
如图,在对称轴右边处,桥洞离水面的高是多少?
19. 本小题分
今年我国多个省市遭受严重干旱,受旱灾的影响,月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
周数
价格元千克
请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出月份与的函数关系式;
进入月,由于本地蔬菜的上市,此种蔬菜的平均销售价格元千克从月第周的元千克下降至第周的元千克,且与周数的变化情况满足二次函数,请求出月份与的函数关系式;
若月份此种蔬菜的进价元千克与周数所满足的函数关系为,月份此种蔬菜的进价元千克与周数所满足的函数关系为试问月份与月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
20. 本小题分
一名同学推铅球,铅球出手后行进过程中离地面的高度单位:与水平距离单位:近似满足函数关系,其图象如图所示.已知铅球落地时的水平距离为.
求铅球出手时离地面的高度;
在铅球行进过程中,当它离地面的高度为时,求此时铅球的水平距离.
21. 本小题分
国庆假期一部长津湖带给我们极大的震撼,面对美军的先进武器,志愿军不怕牺牲,以一敌百,更是有很多技术精湛的“神投手”某志愿军身负重伤,不轻易放弃,用最后一丝力气投出一枚手榴弹,如果把该志愿军投出的手榴弹轨迹作为一抛物线,如图所示,手榴弹飞行的最大高度为米,此时水平飞行距离为米,手榴弹离手点离地面高度为米.
求此抛物线解析式;
求志愿军同志的手榴弹扔了多远?
22. 本小题分
如图,一小球从斜坡上的点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画若小球到达的最高的点坐标为,解答下列问题:
求抛物线的解析式
在斜坡上的点有一棵树,点的横坐标为,树高为,小球能否飞过这棵树通过计算说明理由
求小球在飞行的过程中离斜坡的最大高度.
23. 本小题分
一座拱桥的轮廓是抛物线型如图,拱高,跨度,相邻两支柱间的距离均为.
将抛物线放在所给的直角坐标系中如图,求抛物线的解析式;
求支柱的长度;
拱桥下地平面是双向行车道正中间是一条宽的隔离带,其中的一条行车道能否并排行驶宽、高的三辆汽车汽车间的间隔忽略不计?请说明你的理由.
24. 本小题分
如图是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据范蠡兵法记载:“飞石重二十斤,为机发,行三百步”,其原理蕴含了物理中的“杠杆原理”.
在如图所示的平面直角坐标系中,将投石机置于斜坡的底部原点处,石块从投石机竖直方向上的点处被投出,在斜坡上的点处建有垂直于水平面的城墙已知,石块运动轨迹所在抛物线的顶点坐标是,,,,.
求抛物线的表达式;
通过计算说明石块能否飞越城墙;
分别求出和时,石块与斜坡在竖直方向上的最大距离.
25. 本小题分
某公园要修建一个截面抛物线形的拱门,其最大高度为,宽度为米,现以地面所在的直线为轴建立平面直角坐标系如图所示
求这条抛物线的函数表达式;
如图所示,公园想在抛物线拱门距地面米处钉两个钉子以便拉一条横幅,请计算该横幅的宽度为多少米?
为修建该拱门,施工队需搭建一个矩形“支架“由四根木杆组成,使,两点在抛物线上.,两点在地面上如图所示,请你帮施工队计算一下最多需要准备多少米该种木杆?
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,从地面竖直向上抛出一个小球,小球的高度单位: 与小球运动时间单位:之间的函数关系式为,那么小球从抛出至回落到地面所需的时间是( )
A. B. C. D.
2. 在月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是( )
A. 月份 B. 月份 C. 月份 D. 月份
3. 河北省赵县的赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为,当水面离桥拱顶的高度是时,这时水面宽度为( )
A. B. C. D.
4. 如图,在正方形中,,为对角线上一动点,为射线上一点,若,则的面积最大值为( )
A. B. C. D.
5. 运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线可以看作是一条抛物线,不考虑空气阻力,足球距离地面的高度单位:与足球被踢出后经过的时间单位:近似满足函数关系如图记录了个时刻的数据,根据函数模型和所给数据,可推断出足球飞行到最高点时,最接近的时刻是( )
A. B. C. D.
6. 已知直角三角形中两条直角边长的和为,则当三角形的面积最大时,其中一条直角边长为( )
A. B. C. D.
7. 如图,小明想用长为米的栅栏虚线部分,借助围墙围墙足够长围成一个矩形花园,则矩形的最大面积是( )
A. 平方米 B. 平方米 C. 平方米 D. 平方米
8. 如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度单位:与飞行时间单位:之间具有函数关系下列叙述正确的是( )
A. 小球的飞行高度不能达到 B. 小球的飞行高度可以达到
C. 小球从飞出到落地要用时 D. 小球飞出时的飞行高度为
二、填空题(本大题共8小题,共24分)
9. 边长为的正方形在平面直角坐标系中的位置如图所示,点是边的中点,连接,点在第一象限,且,以直线为对称轴的抛物线过,两点.点为直线上一动点,点为抛物线上一动点,当以点,,,为顶点的四边形是平行四边形时点的坐标为 .
10. 斜抛小球,小球触地后呈抛物线反弹,每次反弹后保持保同的抛物线形状开口方向与开口大小前后一致,第一次反弹后的最大高度为,第二次反弹后的最大高度为,第二次反弹后,小球越过最高点落在垂直于地面的挡板处,且离地高度,若,,则为 .
11. 一座拱桥的轮廓是抛物线型如图所示,桥高为米,拱高米,跨度米.相邻两支柱间的距离均为米,则支柱的高度为 米.
12. 如图,矩形中,点是的中点,点是上的任意一点不与,重合连接,以为斜边,构造等腰,点在矩形内部,连接,若,,则的取值范围为 .
13. 音乐喷泉图可以使喷水造型随音乐的节奏起伏变化而变化,某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边,音乐变化时,抛物线的顶点在直线上变动,从而产生一组不同的抛物线图,这组抛物线的统一形式为若要求喷出的抛物线水线不能到岸边,则的取值范围为___ ____.
14. 如图,矩形中,,动点从点出发,以的速度沿向终点移动,设移动时间为连接,以为一边作正方形,连接、,则面积最小值为 .
15. 如图,线段,点是线段上的一个动点,分别以和为边在线段的同侧构造菱形和菱形,且,是菱形的对角线交点、是菱形的对角线交点,连接,则线段的最小值为 .
16. 一种包装盒的设计方法如图所示,是边长为的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得、、、四点重合于图中的点,形成一个底面为正方形的长方体包装盒,要使包装盒的侧面积最大,则应取 .
三、解答题(本大题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17. 本小题分
如图,地面上两根等长立柱,之间悬挂一根近似成抛物线的绳子.
求绳子最低点离地面的距离;
因实际需要,在离为米的位置处用一根立柱撑起绳子如图,使左边抛物线的最低点距为米,离地面米,求的长;
将立柱的长度提升为米,通过调整的位置,使抛物线对应函数的二次项系数始终为,设离的距离为,抛物线的顶点离地面距离为,当时,求的取值范围.
18. 本小题分
有一个抛物线的拱形桥洞,桥洞离水面的最大高度为,跨度为,如图所示,把它的图形放在直角坐标系中
求这条抛物线所对应的函数关系式;
如图,在对称轴右边处,桥洞离水面的高是多少?
19. 本小题分
今年我国多个省市遭受严重干旱,受旱灾的影响,月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
周数
价格元千克
请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出月份与的函数关系式;
进入月,由于本地蔬菜的上市,此种蔬菜的平均销售价格元千克从月第周的元千克下降至第周的元千克,且与周数的变化情况满足二次函数,请求出月份与的函数关系式;
若月份此种蔬菜的进价元千克与周数所满足的函数关系为,月份此种蔬菜的进价元千克与周数所满足的函数关系为试问月份与月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
20. 本小题分
一名同学推铅球,铅球出手后行进过程中离地面的高度单位:与水平距离单位:近似满足函数关系,其图象如图所示.已知铅球落地时的水平距离为.
求铅球出手时离地面的高度;
在铅球行进过程中,当它离地面的高度为时,求此时铅球的水平距离.
21. 本小题分
国庆假期一部长津湖带给我们极大的震撼,面对美军的先进武器,志愿军不怕牺牲,以一敌百,更是有很多技术精湛的“神投手”某志愿军身负重伤,不轻易放弃,用最后一丝力气投出一枚手榴弹,如果把该志愿军投出的手榴弹轨迹作为一抛物线,如图所示,手榴弹飞行的最大高度为米,此时水平飞行距离为米,手榴弹离手点离地面高度为米.
求此抛物线解析式;
求志愿军同志的手榴弹扔了多远?
22. 本小题分
如图,一小球从斜坡上的点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数刻画若小球到达的最高的点坐标为,解答下列问题:
求抛物线的解析式
在斜坡上的点有一棵树,点的横坐标为,树高为,小球能否飞过这棵树通过计算说明理由
求小球在飞行的过程中离斜坡的最大高度.
23. 本小题分
一座拱桥的轮廓是抛物线型如图,拱高,跨度,相邻两支柱间的距离均为.
将抛物线放在所给的直角坐标系中如图,求抛物线的解析式;
求支柱的长度;
拱桥下地平面是双向行车道正中间是一条宽的隔离带,其中的一条行车道能否并排行驶宽、高的三辆汽车汽车间的间隔忽略不计?请说明你的理由.
24. 本小题分
如图是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据范蠡兵法记载:“飞石重二十斤,为机发,行三百步”,其原理蕴含了物理中的“杠杆原理”.
在如图所示的平面直角坐标系中,将投石机置于斜坡的底部原点处,石块从投石机竖直方向上的点处被投出,在斜坡上的点处建有垂直于水平面的城墙已知,石块运动轨迹所在抛物线的顶点坐标是,,,,.
求抛物线的表达式;
通过计算说明石块能否飞越城墙;
分别求出和时,石块与斜坡在竖直方向上的最大距离.
25. 本小题分
某公园要修建一个截面抛物线形的拱门,其最大高度为,宽度为米,现以地面所在的直线为轴建立平面直角坐标系如图所示
求这条抛物线的函数表达式;
如图所示,公园想在抛物线拱门距地面米处钉两个钉子以便拉一条横幅,请计算该横幅的宽度为多少米?
为修建该拱门,施工队需搭建一个矩形“支架“由四根木杆组成,使,两点在抛物线上.,两点在地面上如图所示,请你帮施工队计算一下最多需要准备多少米该种木杆?
同课章节目录
