第一章 三角形 1 认识三角形 第1课时 三角形的内角和 同步训练(含答案)
文档属性
| 名称 | 第一章 三角形 1 认识三角形 第1课时 三角形的内角和 同步训练(含答案) | 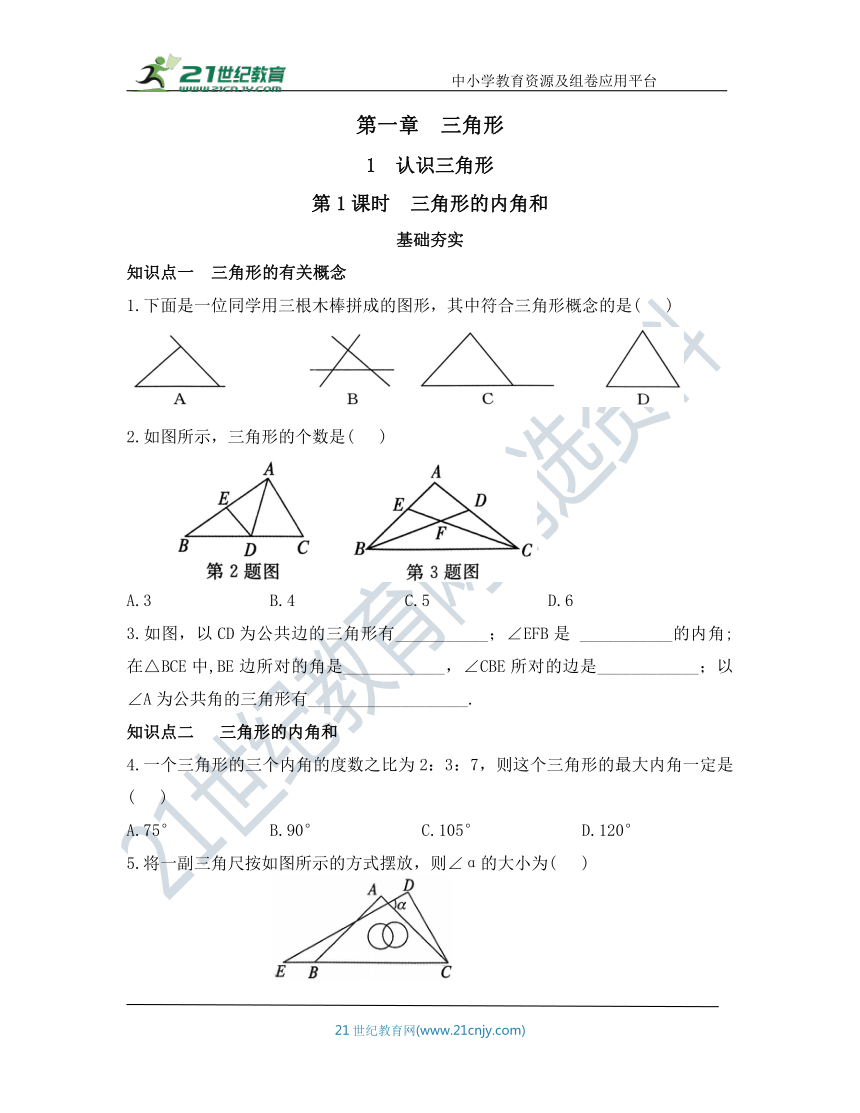 | |
| 格式 | docx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 11:26:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章 三角形
1 认识三角形
第1课时 三角形的内角和
基础夯实
知识点一 三角形的有关概念
1.下面是一位同学用三根木棒拼成的图形,其中符合三角形概念的是( )
2.如图所示,三角形的个数是( )
A.3 B.4 C.5 D.6
3.如图,以CD为公共边的三角形有___________;∠EFB是 ___________的内角;在△BCE中,BE边所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形有___________________.
知识点二 三角形的内角和
4.一个三角形的三个内角的度数之比为2:3:7,则这个三角形的最大内角一定是( )
A.75° B.90° C.105° D.120°
5.将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.85° B.75° C.65° D.60°
6.在△ABC中,若∠A=30°,∠B=50°,则∠C=_____________.
7.已知在△ABC中,∠A=60°,∠B比∠A 小15°,求∠C 的度数.
能力提升
8.已知在△ABC中,∠A=∠B,若∠C=40°,则∠B的度数为( )
A.40° B.60° C.70° D.80°
9.如果一个三角形的三个内角都不相等,那么最小角一定小于( )
A.60° B.59° C.45° D.30°
10.如图,螳螂亦称刀螂,无脊椎动物,属肉食性昆虫.在螳螂的示意 图中,AB∥DE,∠A=∠ACB,若∠ABC=124°,∠CDE=72°,则∠ACD的度数为( )
A.16° B.28° C.44° D.45°
11.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC 为公共边的“共边三角形”有__________对.
12.在△ABC中,三个内角∠A,∠B,∠C满足∠A=3∠B-∠C,则∠B=____________.
13.直线 1∥ ,一块含45°角的直角三角尺如图放置,若∠1=85°,则∠2=_.
14.如图,在△ABC中,BC边不动,点A 竖直向上运动,∠A 越来越小,∠B,∠C越来越大.若∠A减小α度,∠B增加β度,∠C 增加γ度,则α,β,γ三者之间的等量关系是________________.
15.如图,按规定,一块模板中 AB,CD的延长线应相交成85°的角.因交点不在板上,不便测量,工人师傅连接 AC,测得∠BAC=32°,∠DCA=65°,此时AB,CD的延长线相交所成的角是否符合规定 为什么
16.如图,AB∥CD,直线 l分别交AB,CD于点E,F,点M在线段 EF上,N是直线CD上的一个动点(点 N不与点 F 重合).
(1)当点 N在射线 FC上运动时,∠FMN+∠FNM=∠AEF,说明理由;
(2)当点 N在射线 FD上运动时,∠FMN+∠FNM 与∠AEF有什么关系 并说明理由.
核心拓展
17.取一副三角尺按如图所示拼接,固定三角尺ADC,将三角尺 ABC绕点 A 顺时针方向旋转,旋转角度为α(0°<α≤45°),得到
(1)当α=_度时,AB∥DC;当旋转到图3所示位置时,α=___________度;
(2)连接 BD,当0°<a≤45°时, α+∠BDC 值的大小是否发生变化 为什么
参考答案
1. D【解析】三角形是由不在同一直线上的三条线段首尾顺次相接所成的图形,只有选项D符合题意.
2. C
3.△CDF,△BCD △BEF ∠BCE CE △ABD,△ACE,△ABC
4. C 【解析】这个三角形的最大内角为 =105°.
5. B
6.100°【解析】∠C=180°-∠A-∠B=180°-30°-50°=100°.
7.解:根据题意,得∠B=∠A-15°=60°-15°=45°.
又因为∠A+∠B+∠C=180°,所以 60°+45°+∠C=180°,
解得∠C=75°.
8. C【解析】∠B=(180°-40°)÷2=70°.
9. A 【解析】若最小角大于或等于60°,则另外两个角一定也大于60°,那么此三角形内角和大于 180°,不符合三角形的内角和为 180°,所以此三角形的最小角一定要小于60°.
10. C 11.3 12.45° 13.40°
14.α=β+γ【解析】因为三角形的内角和是定值 180°,所以∠A+∠B+∠C=180°,所以当∠A越来越小,∠B,∠C 越来越大时,则有∠A-α+∠B+β+∠C+γ=180°,
即α=β+γ.
15.解:AB,CD的延长线相交所成的角不符合规定.理由如下:
如图,延长AB,CD交于点O,
在△AOC中,因为∠BAC=32°,∠DCA=65°,
所以∠AOC=180°-∠BAC-∠DCA=180°-32°-65°=83°<85°.
所以此模板不符合规定.
16.解:(1)因为 AB∥CD,所以∠AEF+∠MFN=180°.
因为∠MFN+∠FMN+∠FNM=180°,所以∠FMN+∠FNM=∠AEF.
(2)∠FMN +∠FNM +∠AEF=180°.理由如下:
如图,因为 AB∥CD,所以∠AEF=∠MFN.
因为∠MFN +∠FMN+∠FNM=180°,
所以∠FMN+∠FNM+∠AEF=180°.
17.解:(1)因为AB∥CD,所以∠CAB=∠ACD=30°.
所以
当旋转到图 3所示位置时,
故答案为:15;45.
值的大小不变.
理由:如图,在△DAB中,
因为∠DAB+∠ABD+∠ADB=180°,
即 ∠BDC=180°,
所以
即 值的大小不变.
21世纪教育网(www.21cnjy.com)
第一章 三角形
1 认识三角形
第1课时 三角形的内角和
基础夯实
知识点一 三角形的有关概念
1.下面是一位同学用三根木棒拼成的图形,其中符合三角形概念的是( )
2.如图所示,三角形的个数是( )
A.3 B.4 C.5 D.6
3.如图,以CD为公共边的三角形有___________;∠EFB是 ___________的内角;在△BCE中,BE边所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形有___________________.
知识点二 三角形的内角和
4.一个三角形的三个内角的度数之比为2:3:7,则这个三角形的最大内角一定是( )
A.75° B.90° C.105° D.120°
5.将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.85° B.75° C.65° D.60°
6.在△ABC中,若∠A=30°,∠B=50°,则∠C=_____________.
7.已知在△ABC中,∠A=60°,∠B比∠A 小15°,求∠C 的度数.
能力提升
8.已知在△ABC中,∠A=∠B,若∠C=40°,则∠B的度数为( )
A.40° B.60° C.70° D.80°
9.如果一个三角形的三个内角都不相等,那么最小角一定小于( )
A.60° B.59° C.45° D.30°
10.如图,螳螂亦称刀螂,无脊椎动物,属肉食性昆虫.在螳螂的示意 图中,AB∥DE,∠A=∠ACB,若∠ABC=124°,∠CDE=72°,则∠ACD的度数为( )
A.16° B.28° C.44° D.45°
11.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC 为公共边的“共边三角形”有__________对.
12.在△ABC中,三个内角∠A,∠B,∠C满足∠A=3∠B-∠C,则∠B=____________.
13.直线 1∥ ,一块含45°角的直角三角尺如图放置,若∠1=85°,则∠2=_.
14.如图,在△ABC中,BC边不动,点A 竖直向上运动,∠A 越来越小,∠B,∠C越来越大.若∠A减小α度,∠B增加β度,∠C 增加γ度,则α,β,γ三者之间的等量关系是________________.
15.如图,按规定,一块模板中 AB,CD的延长线应相交成85°的角.因交点不在板上,不便测量,工人师傅连接 AC,测得∠BAC=32°,∠DCA=65°,此时AB,CD的延长线相交所成的角是否符合规定 为什么
16.如图,AB∥CD,直线 l分别交AB,CD于点E,F,点M在线段 EF上,N是直线CD上的一个动点(点 N不与点 F 重合).
(1)当点 N在射线 FC上运动时,∠FMN+∠FNM=∠AEF,说明理由;
(2)当点 N在射线 FD上运动时,∠FMN+∠FNM 与∠AEF有什么关系 并说明理由.
核心拓展
17.取一副三角尺按如图所示拼接,固定三角尺ADC,将三角尺 ABC绕点 A 顺时针方向旋转,旋转角度为α(0°<α≤45°),得到
(1)当α=_度时,AB∥DC;当旋转到图3所示位置时,α=___________度;
(2)连接 BD,当0°<a≤45°时, α+∠BDC 值的大小是否发生变化 为什么
参考答案
1. D【解析】三角形是由不在同一直线上的三条线段首尾顺次相接所成的图形,只有选项D符合题意.
2. C
3.△CDF,△BCD △BEF ∠BCE CE △ABD,△ACE,△ABC
4. C 【解析】这个三角形的最大内角为 =105°.
5. B
6.100°【解析】∠C=180°-∠A-∠B=180°-30°-50°=100°.
7.解:根据题意,得∠B=∠A-15°=60°-15°=45°.
又因为∠A+∠B+∠C=180°,所以 60°+45°+∠C=180°,
解得∠C=75°.
8. C【解析】∠B=(180°-40°)÷2=70°.
9. A 【解析】若最小角大于或等于60°,则另外两个角一定也大于60°,那么此三角形内角和大于 180°,不符合三角形的内角和为 180°,所以此三角形的最小角一定要小于60°.
10. C 11.3 12.45° 13.40°
14.α=β+γ【解析】因为三角形的内角和是定值 180°,所以∠A+∠B+∠C=180°,所以当∠A越来越小,∠B,∠C 越来越大时,则有∠A-α+∠B+β+∠C+γ=180°,
即α=β+γ.
15.解:AB,CD的延长线相交所成的角不符合规定.理由如下:
如图,延长AB,CD交于点O,
在△AOC中,因为∠BAC=32°,∠DCA=65°,
所以∠AOC=180°-∠BAC-∠DCA=180°-32°-65°=83°<85°.
所以此模板不符合规定.
16.解:(1)因为 AB∥CD,所以∠AEF+∠MFN=180°.
因为∠MFN+∠FMN+∠FNM=180°,所以∠FMN+∠FNM=∠AEF.
(2)∠FMN +∠FNM +∠AEF=180°.理由如下:
如图,因为 AB∥CD,所以∠AEF=∠MFN.
因为∠MFN +∠FMN+∠FNM=180°,
所以∠FMN+∠FNM+∠AEF=180°.
17.解:(1)因为AB∥CD,所以∠CAB=∠ACD=30°.
所以
当旋转到图 3所示位置时,
故答案为:15;45.
值的大小不变.
理由:如图,在△DAB中,
因为∠DAB+∠ABD+∠ADB=180°,
即 ∠BDC=180°,
所以
即 值的大小不变.
21世纪教育网(www.21cnjy.com)
