第一章 三角形 1 认识三角形 第5课时 三角形的高线 同步训练(含答案)
文档属性
| 名称 | 第一章 三角形 1 认识三角形 第5课时 三角形的高线 同步训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 11:31:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
1 认识三角形
第5课时 三角形的高线
基础夯实
知识点一 三角形的高及画法
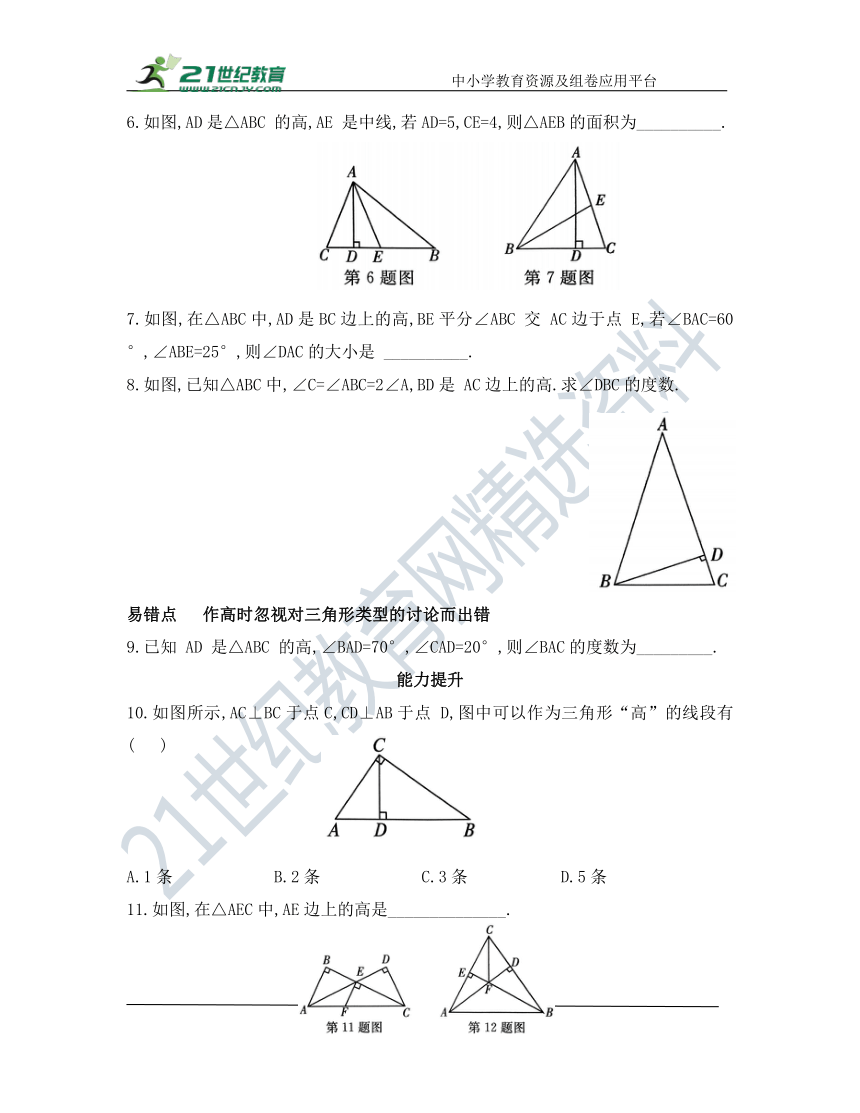
1.用三角尺作△ABC的边BC 上的高,下列三角尺的摆放位置正确的是( )
2.如图,AD⊥BC,GC⊥BC,CF⊥AB,点 D,C,F是垂足,则下列说法中错误的是( )
A.在△ABC中,AD是 BC边上的高 B.在△ABC中,CF是AB边上的高
C.在△GBC中,GC 是 BC边上的高 D.在△GBC中,GC 是 BG边上的高
3.如图,以AD为高的三角形共有_____________个.
知识点二 三角形的高的位置
4.一张三角形纸片上,小新只能折叠出它的一条高,可以推断,这个三角形纸片是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.直角或钝角三角形
5.若一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都不对
知识点三 三角形高的有关计算
6.如图,AD是△ABC 的高,AE 是中线,若AD=5,CE=4,则△AEB的面积为__________.
7.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC 交 AC边于点 E,若∠BAC=60°,∠ABE=25°,则∠DAC的大小是 __________.
8.如图,已知△ABC中,∠C=∠ABC=2∠A,BD是 AC边上的高.求∠DBC的度数.
易错点 作高时忽视对三角形类型的讨论而出错
9.已知 AD 是△ABC 的高,∠BAD=70°,∠CAD=20°,则∠BAC的度数为_________.
能力提升
10.如图所示,AC⊥BC于点C,CD⊥AB于点 D,图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
11.如图,在△AEC中,AE边上的高是______________.
12.如图,在△ABC中,AD⊥BC,垂足为点 D,BE⊥AC,垂足为点 E,AD,BE 相交于点F,连接 CF.若∠ABE=28°,则∠ACF=_______________°.
13.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为____________.
14.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BDE中作BD边上的高;
(2)若△ABC 的面积为 40,BD=5,求△BDE中BD边上的高.
15.如图所示,已知 AD,AE分别是△ABC 的高和中线,AB=6cm,AC=8cm,BC=10 cm,
∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
核心拓展
(1)如图①,在△ABC中,点 D,E在边 BC上,AD平分∠BAC,AE⊥BC,∠B=35°,
∠C=65°,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA 延长线上一点,FE⊥BC”,其
他条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其他条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论
参考答案
1. A 2. D 3.6 4. D 5. C
6.10【解析】由题意得BE=CE=4.又因为高AD=5,所以
7.20°【解析】因为 BE 平分∠ABC交AC 边于点E,∠ABE=25°,所以∠ABC=50°.又因为∠BAC=60°,所以∠C=70°.因为 AD是BC 边上的高,所以∠ADC=90°.
所以∠DAC=20°.
8.解:设∠A=x°,则∠C=∠ABC=2x°,所以x+2x+2x=180.
解得x=36.所以∠C=72°.
在△BDC中,因为∠BDC=90°,所以∠DBC=90°-∠C =90°-72°=18°.
9.90°或50° 10. D 11. CD
12.28 【解析】∠EAB=90°-28°=62°,延长CF交AB 于点M,由于三角形三条高所在的直线交于一点,故 CF⊥AB,则∠ACF=90°—∠EAB=90°—62°=28°.
13.60°或120°【解析】当该等腰三角形是锐角三角形时,顶角的度数为60°;当该等腰三角形是钝角三角形时,顶角的度数为 120°.
14.解:(1)如图,过点E作边BD 的垂线 EF,垂足是点 F.
EF即为△BDE中BD边上的高.
(2)因为 AD是△ABC 的中线,所以
同理,BE 是△ABD的中线, 所以
因为 所以 即
又因为△ABC的面积为 40,BD=5,所以EF=4.
故△BDE中BD边上的高是4.
15.解:(1)因为∠BAC=90°,AD是边 BC 上的高,所以
所以 即AD的长度为 4.8 cm.
(2)方法一:因为△ABC 是直角三角形,∠BAC=90°,AB=6 cm,AC=8cm,
所以
又因为AE 是边BC 的中线,所以 BE=EC.
所以 即
所以
所以△ABE的面积是 12cm .
方法二:因为 ,由(1)知AD=4.8cm,
所以
所以△ABE 的面积是 12 cm .
(3)因为AE为BC 边上的中线,所以BE=CE,
所以△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是 2cm .
16.解:(1)因为∠B=35°,∠C=65°,
所以∠BAC=180°-∠B-∠C=180°-35°-65°=80°.
因为AD平分∠BAC,所以
因为 AE⊥BC,所以∠AEB=90°.所以∠BAE=90°-∠B=90°-35°=55°.
所以∠DAE=∠BAE-∠BAD=55°-40°=15°.
(2)过点 A 作AH⊥BC 于点 H,如图①所示,由(1)得∠DAH=15°.
因为 FE⊥BC,所以AH∥EF.所以∠DFE=∠DAH=15°.
(3)作出图形如图②所示,过点A作AH⊥BC于点H,由(1)得∠DAH=15°.
因为 FE⊥BC,所以AH∥EF.所以∠DFE=∠DAH=15°.
(4)结合上述三个问题的解决过程得:∠BAC的平分线与平分线所在直线上的点作BC的垂线的夹角为 15°.
21世纪教育网(www.21cnjy.com)
第一章 三角形
1 认识三角形
第5课时 三角形的高线
基础夯实
知识点一 三角形的高及画法
1.用三角尺作△ABC的边BC 上的高,下列三角尺的摆放位置正确的是( )
2.如图,AD⊥BC,GC⊥BC,CF⊥AB,点 D,C,F是垂足,则下列说法中错误的是( )
A.在△ABC中,AD是 BC边上的高 B.在△ABC中,CF是AB边上的高
C.在△GBC中,GC 是 BC边上的高 D.在△GBC中,GC 是 BG边上的高
3.如图,以AD为高的三角形共有_____________个.
知识点二 三角形的高的位置
4.一张三角形纸片上,小新只能折叠出它的一条高,可以推断,这个三角形纸片是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.直角或钝角三角形
5.若一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.以上都不对
知识点三 三角形高的有关计算
6.如图,AD是△ABC 的高,AE 是中线,若AD=5,CE=4,则△AEB的面积为__________.
7.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC 交 AC边于点 E,若∠BAC=60°,∠ABE=25°,则∠DAC的大小是 __________.
8.如图,已知△ABC中,∠C=∠ABC=2∠A,BD是 AC边上的高.求∠DBC的度数.
易错点 作高时忽视对三角形类型的讨论而出错
9.已知 AD 是△ABC 的高,∠BAD=70°,∠CAD=20°,则∠BAC的度数为_________.
能力提升
10.如图所示,AC⊥BC于点C,CD⊥AB于点 D,图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
11.如图,在△AEC中,AE边上的高是______________.
12.如图,在△ABC中,AD⊥BC,垂足为点 D,BE⊥AC,垂足为点 E,AD,BE 相交于点F,连接 CF.若∠ABE=28°,则∠ACF=_______________°.
13.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为____________.
14.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BDE中作BD边上的高;
(2)若△ABC 的面积为 40,BD=5,求△BDE中BD边上的高.
15.如图所示,已知 AD,AE分别是△ABC 的高和中线,AB=6cm,AC=8cm,BC=10 cm,
∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
核心拓展
(1)如图①,在△ABC中,点 D,E在边 BC上,AD平分∠BAC,AE⊥BC,∠B=35°,
∠C=65°,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA 延长线上一点,FE⊥BC”,其
他条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其他条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论
参考答案
1. A 2. D 3.6 4. D 5. C
6.10【解析】由题意得BE=CE=4.又因为高AD=5,所以
7.20°【解析】因为 BE 平分∠ABC交AC 边于点E,∠ABE=25°,所以∠ABC=50°.又因为∠BAC=60°,所以∠C=70°.因为 AD是BC 边上的高,所以∠ADC=90°.
所以∠DAC=20°.
8.解:设∠A=x°,则∠C=∠ABC=2x°,所以x+2x+2x=180.
解得x=36.所以∠C=72°.
在△BDC中,因为∠BDC=90°,所以∠DBC=90°-∠C =90°-72°=18°.
9.90°或50° 10. D 11. CD
12.28 【解析】∠EAB=90°-28°=62°,延长CF交AB 于点M,由于三角形三条高所在的直线交于一点,故 CF⊥AB,则∠ACF=90°—∠EAB=90°—62°=28°.
13.60°或120°【解析】当该等腰三角形是锐角三角形时,顶角的度数为60°;当该等腰三角形是钝角三角形时,顶角的度数为 120°.
14.解:(1)如图,过点E作边BD 的垂线 EF,垂足是点 F.
EF即为△BDE中BD边上的高.
(2)因为 AD是△ABC 的中线,所以
同理,BE 是△ABD的中线, 所以
因为 所以 即
又因为△ABC的面积为 40,BD=5,所以EF=4.
故△BDE中BD边上的高是4.
15.解:(1)因为∠BAC=90°,AD是边 BC 上的高,所以
所以 即AD的长度为 4.8 cm.
(2)方法一:因为△ABC 是直角三角形,∠BAC=90°,AB=6 cm,AC=8cm,
所以
又因为AE 是边BC 的中线,所以 BE=EC.
所以 即
所以
所以△ABE的面积是 12cm .
方法二:因为 ,由(1)知AD=4.8cm,
所以
所以△ABE 的面积是 12 cm .
(3)因为AE为BC 边上的中线,所以BE=CE,
所以△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是 2cm .
16.解:(1)因为∠B=35°,∠C=65°,
所以∠BAC=180°-∠B-∠C=180°-35°-65°=80°.
因为AD平分∠BAC,所以
因为 AE⊥BC,所以∠AEB=90°.所以∠BAE=90°-∠B=90°-35°=55°.
所以∠DAE=∠BAE-∠BAD=55°-40°=15°.
(2)过点 A 作AH⊥BC 于点 H,如图①所示,由(1)得∠DAH=15°.
因为 FE⊥BC,所以AH∥EF.所以∠DFE=∠DAH=15°.
(3)作出图形如图②所示,过点A作AH⊥BC于点H,由(1)得∠DAH=15°.
因为 FE⊥BC,所以AH∥EF.所以∠DFE=∠DAH=15°.
(4)结合上述三个问题的解决过程得:∠BAC的平分线与平分线所在直线上的点作BC的垂线的夹角为 15°.
21世纪教育网(www.21cnjy.com)
