等腰三角形的性质(1)[上学期]
文档属性
| 名称 | 等腰三角形的性质(1)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 307.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-06 09:08:00 | ||
图片预览






文档简介
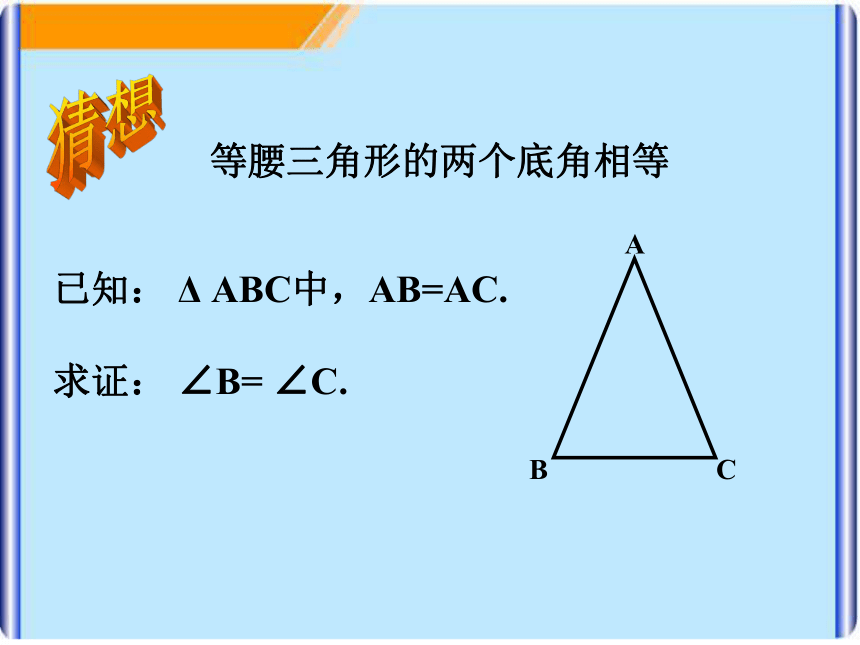
课件17张PPT。等腰三角形的性质(1)等腰三角形的两个底角相等已知: Δ ABC中,AB=AC.
求证: ∠B= ∠C.猜想证明:作顶角的平分线AD. 在△BAD和△CAD中,AB=AC ( 已知 ),∠ 1= ∠ 2 ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.12证明:等腰三角形的两个底角相等作顶角的平分线D证明: 作底边中线AD.
在△BAD和△CAD中,AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.D证明:等腰三角形的两个底角相等作底边中线证明: 作底边高线AD.
在Rt△BAD和△RtCAD中,AB=AC ( 已知 ),AD=AD (公共边) ,∴ Rt △BAD ≌ Rt △CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.D证明:等腰三角形的两个底角相等作底边的高线等腰三角形的性质定理等腰三角形的两个底角相等(简写成“等边对等角”) 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边. 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.“三线合一”在△ ABC中,AB=AC=BC,利用已有的知识,如何推导出
∠A、 ∠B 、∠C 的度数. 推论2 等边三角形的各角都相等,并且每一个角都
等于60 o .
⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为
__________________.⒊等腰三角形一个角为110°,它的另外两个角为_______.① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,40 °35 °,35 °70°,40°或55°,55° 4. 根据等腰三角形性质定理的推论,在△ABC中, AB=AC时, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD例1 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
例2:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.解: ∵AB=AC,BD=BC=AD
∴∠ABC= ∠ C= ∠ BDC,
∠ A= ∠ ABD
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x
从而∠ABC= ∠C=BDC=2x
在△ABC中,有
∠A+ ∠ABC+ ∠C=x+2x+2x=1800
解得x=360
在△ABC中, ∠A=360, ∠ABC= ∠C=720探究一请动手画一个等腰三角形,并画出底边中点到两腰的距离,猜猜这两条距离有什么关系?你能用所学的知识解释吗?可将等腰三角形△ABC沿对称轴AD折叠DE=DF等腰三角形底边中点到两腰的距离。探究二 ①如果DE、DF分别是AB、AC上的中线,此时还有DE=DF吗?②如果DE、DF分别是∠ADB、∠ADC的角平分线,此时还有DE=DF吗?已知:如图, △ ABC中, ∠ABC=50 o, ∠ACB=80 o,延长
CB至D,使BD=BA,延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .ABCDE1、研究有关等腰三角形的问题,顶角平分线、底边中线,底边的高是常用的辅助线;2、熟练求解等腰三角形的顶角、底角的度数;
3、掌握等腰三角形三线合一的应用。再 见
求证: ∠B= ∠C.猜想证明:作顶角的平分线AD. 在△BAD和△CAD中,AB=AC ( 已知 ),∠ 1= ∠ 2 ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.12证明:等腰三角形的两个底角相等作顶角的平分线D证明: 作底边中线AD.
在△BAD和△CAD中,AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.D证明:等腰三角形的两个底角相等作底边中线证明: 作底边高线AD.
在Rt△BAD和△RtCAD中,AB=AC ( 已知 ),AD=AD (公共边) ,∴ Rt △BAD ≌ Rt △CAD (HL).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.D证明:等腰三角形的两个底角相等作底边的高线等腰三角形的性质定理等腰三角形的两个底角相等(简写成“等边对等角”) 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边. 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.“三线合一”在△ ABC中,AB=AC=BC,利用已有的知识,如何推导出
∠A、 ∠B 、∠C 的度数. 推论2 等边三角形的各角都相等,并且每一个角都
等于60 o .
⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为
__________________.⒊等腰三角形一个角为110°,它的另外两个角为_______.① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,40 °35 °,35 °70°,40°或55°,55° 4. 根据等腰三角形性质定理的推论,在△ABC中, AB=AC时, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD例1 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
例2:如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.解: ∵AB=AC,BD=BC=AD
∴∠ABC= ∠ C= ∠ BDC,
∠ A= ∠ ABD
设∠A=x,则∠BDC= ∠A+ ∠ABD=2x
从而∠ABC= ∠C=BDC=2x
在△ABC中,有
∠A+ ∠ABC+ ∠C=x+2x+2x=1800
解得x=360
在△ABC中, ∠A=360, ∠ABC= ∠C=720探究一请动手画一个等腰三角形,并画出底边中点到两腰的距离,猜猜这两条距离有什么关系?你能用所学的知识解释吗?可将等腰三角形△ABC沿对称轴AD折叠DE=DF等腰三角形底边中点到两腰的距离。探究二 ①如果DE、DF分别是AB、AC上的中线,此时还有DE=DF吗?②如果DE、DF分别是∠ADB、∠ADC的角平分线,此时还有DE=DF吗?已知:如图, △ ABC中, ∠ABC=50 o, ∠ACB=80 o,延长
CB至D,使BD=BA,延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .ABCDE1、研究有关等腰三角形的问题,顶角平分线、底边中线,底边的高是常用的辅助线;2、熟练求解等腰三角形的顶角、底角的度数;
3、掌握等腰三角形三线合一的应用。再 见
