西藏拉萨市2022-2023学年高二下学期期末联考数学(文)试题(PDF版无答案)
文档属性
| 名称 | 西藏拉萨市2022-2023学年高二下学期期末联考数学(文)试题(PDF版无答案) |
|
|
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 00:00:00 | ||
图片预览


文档简介
2022-2023 学年第二学期拉萨市高中期末联考
高二数学(文) 试题
注意事项:
1. 本试卷满分 150 分,考试时间 120 分钟。
2. 答卷前,考生务必将自己的姓名、考生号等信息填写在答题卡指定位置上。
3. 作答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用
橡皮擦干净后,再选涂其它答案标号。作答非选择题时,将答案写在答题卡上。写在本试卷上无效。
第Ⅰ卷
一、选择题共 12 小题,每小题 5 分,共 60 分。在每小题列出的四个选项中,
选出符合题目要求的一项。
1.已知集合 A 1,2,3 , B x x 2 ,则 A B ( )
A. B. 3
C. 2,3 D. 2,3
2.复数 z i ( 1 2i)的虚部是( )
A. 1 B.1
C. 2 D. 2
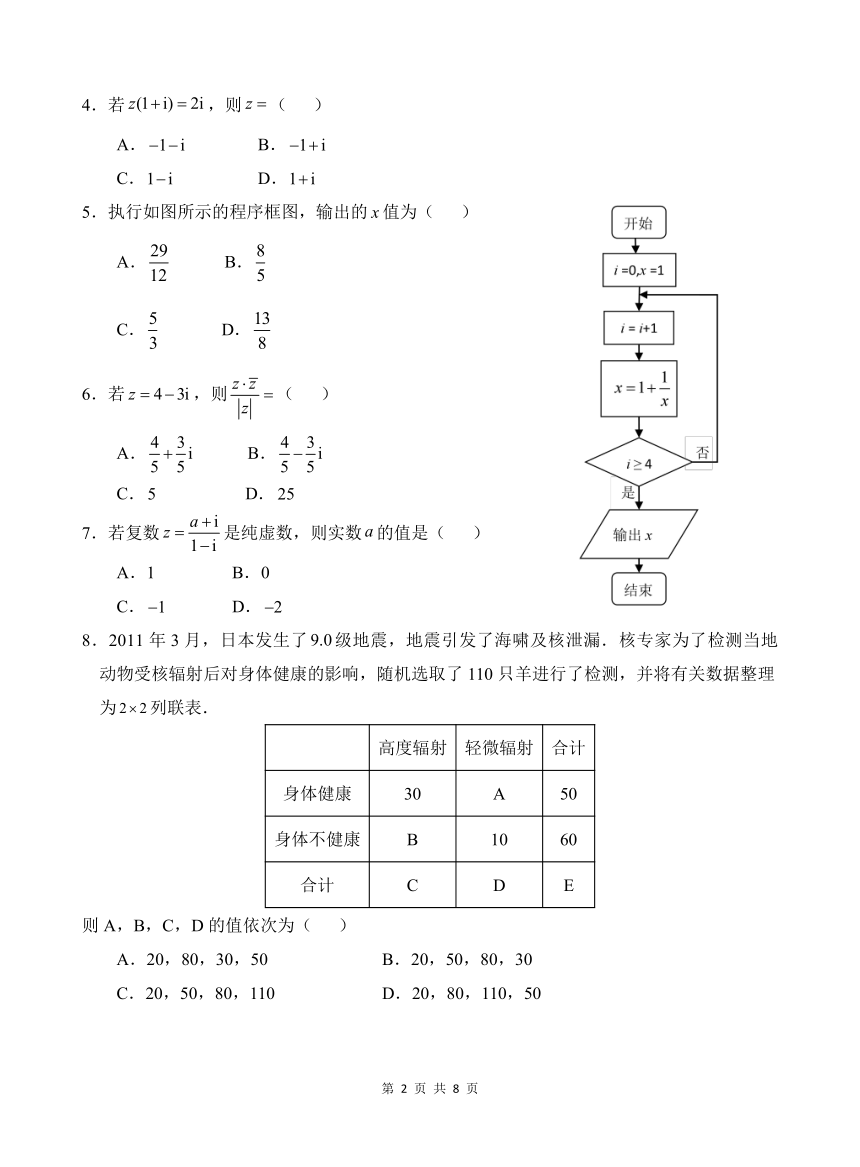
3.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A. r2 r4 0 r3 r1 B. r4 r2 0 r1 r3
C. r4 r2 0 r3 r1 D. r2 r4 0 r1 r3
第 1 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
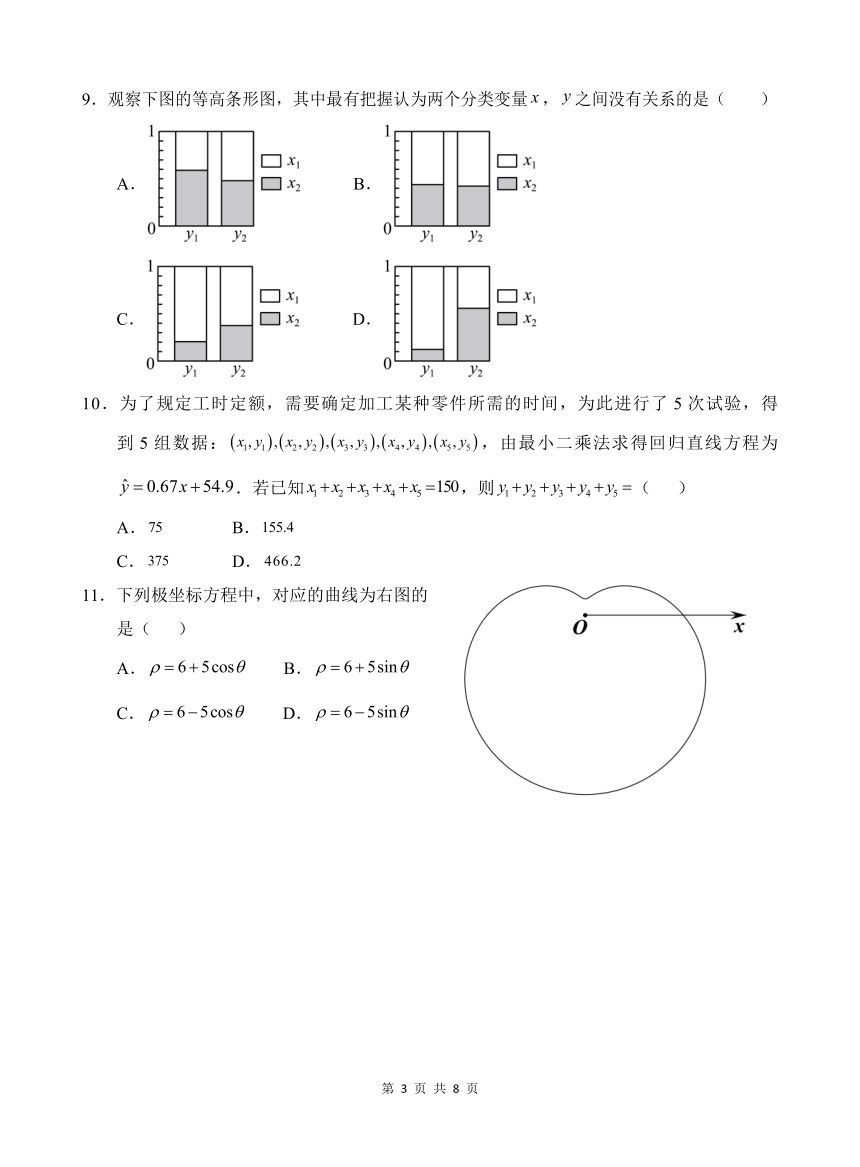
4.若 z(1 i) 2i,则 z ( )
A. 1 i B. 1 i
C.1 i D.1 i
5.执行如图所示的程序框图,输出的 x值为( )
A 29 8. B.
12 5
C 5 13. D.
3 8
6 z z.若 z 4 3i,则 ( )
z
A 4 3 4 3. i B. i
5 5 5 5
C.5 D. 25
a i
7.若复数 z 是纯虚数,则实数 a的值是( )
1 i
A.1 B.0
C. 1 D. 2
8.2011 年 3 月,日本发生了 9.0级地震,地震引发了海啸及核泄漏.核专家为了检测当地
动物受核辐射后对身体健康的影响,随机选取了 110只羊进行了检测,并将有关数据整理
为 2 2列联表.
高度辐射 轻微辐射 合计
身体健康 30 A 50
身体不健康 B 10 60
合计 C D E
则 A,B,C,D的值依次为( )
A.20,80,30,50 B.20,50,80,30
C.20,50,80,110 D.20,80,110,50
第 2 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
9.观察下图的等高条形图,其中最有把握认为两个分类变量 x, y之间没有关系的是( )
A. B.
C. D.
10.为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了 5 次试验,得
到 5 组数据: x1, y1 , x2 , y2 , x3, y3 , x4 , y4 , x5 , y5 ,由最小二乘法求得回归直线方程为
y 0.67x 54.9.若已知 x1 x2 x3 x4 x5 150,则 y1 y2 y3 y4 y5 ( )
A.75 B.155.4
C. 375 D. 466.2
11.下列极坐标方程中,对应的曲线为右图的
是( )
A. 6 5cos B. 6 5sin
C. 6 5cos D. 6 5sin
第 3 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
12.一次数学考试共有 8道判断题,每道题 5分,满分 40分.规定正确的画√,错误的画╳.
甲、乙、丙、丁四名同学的解答及得分情况如表所示,则 m的值为( )
题号
1 2 3 4 5 6 7 8 得分
学生
甲 ╳ √ ╳ √ ╳ ╳ √ ╳ 30
乙 ╳ ╳ √ √ √ ╳ ╳ √ 25
丙 √ ╳ ╳ ╳ √ √ √ ╳ 25
丁 ╳ √ ╳ √ √ ╳ √ √ m
A.35 B.30
C.25 D.20
第Ⅱ卷
二、填空题共 4小题,每小题 5分,共 20 分。
13.拉萨市政府调查市民收入增减与旅游需求的关系时,采用独立性检验法抽查了 5000人,
计算发现K 2 6.109,根据这一数据,市政府断言市民收入增减与旅游需求有关的可信
度是______%.
参考数据:
P K 2 k0 0.15 0.10 0.05 0.025 0.010 0.001
k0 2.072 2.706 3.841 5.024 6.635 10.828
14.1 i i2 i3 i2024 .
A 4, π B 2, π 15.在极坐标系中,点 , ,则线段 AB的长为 .
6 2
16.已知复数 z 1 2i,若 in z( n N*)在复平面内对应的点位于第四象限,写出一个满
足条件的 n是__________.
第 4 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
三、解答题共 6小题,共 70 分。解答应写出文字说明,演算步骤或证明过程。
3 i
17.(共 10分)已知复数 z ( i是虚数单位).
2 i
(1)求复数 z的共轭复数;
2 2( )若 z az b z a,b R ,求 a,b的值.
18.(共 12分)某大学艺术专业 400名学生参加某次测评,根据男、女学生人数比例使用
分层随机抽样的方法从中随机抽取了 100名学生,记录他们的分数,将数据分成 7组:
[20,30),[30,40),…,[80,90],并整理得到如图的频率分布直方图:
(1)估计总体 400名学生中分数小于 60的人数;
(2)已知样本中分数小于 40的学生有 5人,试估计总体中分数在区间[40,50)内的人数.
第 5 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
x 2cos
19.(共 12 分)在平面直角坐标系 xOy中,曲线C的参数方程为 (其中 为
y 2 2sin
参数).以坐标原点为极点, x轴非负半轴为极轴建立极坐标系,直线 l的极坐标方程为
2 cos π 4.
4
(1)求直线 l的直角坐标方程和曲线C的普通方程;
(2)设直线 l与曲线C交于 A,B两点,求线段 AB的长度.
20.(共 12 分)垃圾是人类日常生活和生产中产生的废弃物,由于排出量大,成分复杂多
样,且具有污染性,所以需要无害化、减量化处理.某省为调查产生的垃圾数量,采用
简单随机抽样的方法抽取 20 个县城进行了分析,得到样本数据 xi , yi i 1,2, , 20 ,
其中 xi 和 yi分别表示第 i个县城的人口(单位:万人)和该县年垃圾产生总量(单位:
20 20 20 20
2 2
吨),并计算得 xi 80 , yi 4000 , xi x 80 , yi y 8000 ,
i 1 i 1 i 1 i 1
20
xi x yi y 700.
i 1
(1)求这 20个县年垃圾产生总量的平均值;
(2)请用相关系数说明该组数据中 y与 x之间的关系可用线性回归模型进行拟合.(当
0.75 r 1时, y与 x的相关关系较强,否则相关关系较弱.)
n
xi x yi y
i 1
参考公式:相关系数 r n n .
x 2 2i x yi y
i 1 i 1
第 6 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
21.(共 12 分)随着互联网的发展,网络已成为人们日常学习、工作和生活不可或缺的部
分,互联网在带给人们生活便捷与高效工作的同时,网络犯罪也日益增多.为了防范网
络犯罪与网络诈骗,某学校举办“网络安全宣传倡议”活动.该学校从全体学生中随机抽
取了 100名男生和 100名女生对“网络安全宣传倡议”的了解情况进行问卷调查.下面是
问卷调查得分的频率分布表:
成绩(分) [40,50) [50,60) [60,70) [70,80) [80,90) [90,100]
频率 0.075 0.2 0.3 0.25 0.15 0.025
将得分不低于 70分的学生视作了解,已知有 50名男生问卷调查得分不低于 70分.
(1)根据已知条件完成下面 2 2列联表;
男 女 合计
了解
不了解
合计
(2)判断是否有95%的把握认为对“网络安全宣传倡议”的了解情况与性别有关?
n ad bc 22 参考公式:K ,其中 n a b c d .
a b c d a c b d
参考数据:
P K 2 k0 0.10 0.05 0.010 0.005
k0 2.706 3.841 6.635 7.879
第 7 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
22.(共 12分)如图所示形如花瓣的曲线G称为四叶玫瑰线,在极坐标系中,其极坐标方程
为 2sin 2 .
(1)若射线 l: 与G相交于异于极点O的点P,求 OP ;
6
π
(2)若 A, B为G上的两点,且 AOB ,求 AOB面积的最大值.
4
第 8 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
高二数学(文) 试题
注意事项:
1. 本试卷满分 150 分,考试时间 120 分钟。
2. 答卷前,考生务必将自己的姓名、考生号等信息填写在答题卡指定位置上。
3. 作答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用
橡皮擦干净后,再选涂其它答案标号。作答非选择题时,将答案写在答题卡上。写在本试卷上无效。
第Ⅰ卷
一、选择题共 12 小题,每小题 5 分,共 60 分。在每小题列出的四个选项中,
选出符合题目要求的一项。
1.已知集合 A 1,2,3 , B x x 2 ,则 A B ( )
A. B. 3
C. 2,3 D. 2,3
2.复数 z i ( 1 2i)的虚部是( )
A. 1 B.1
C. 2 D. 2
3.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A. r2 r4 0 r3 r1 B. r4 r2 0 r1 r3
C. r4 r2 0 r3 r1 D. r2 r4 0 r1 r3
第 1 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
4.若 z(1 i) 2i,则 z ( )
A. 1 i B. 1 i
C.1 i D.1 i
5.执行如图所示的程序框图,输出的 x值为( )
A 29 8. B.
12 5
C 5 13. D.
3 8
6 z z.若 z 4 3i,则 ( )
z
A 4 3 4 3. i B. i
5 5 5 5
C.5 D. 25
a i
7.若复数 z 是纯虚数,则实数 a的值是( )
1 i
A.1 B.0
C. 1 D. 2
8.2011 年 3 月,日本发生了 9.0级地震,地震引发了海啸及核泄漏.核专家为了检测当地
动物受核辐射后对身体健康的影响,随机选取了 110只羊进行了检测,并将有关数据整理
为 2 2列联表.
高度辐射 轻微辐射 合计
身体健康 30 A 50
身体不健康 B 10 60
合计 C D E
则 A,B,C,D的值依次为( )
A.20,80,30,50 B.20,50,80,30
C.20,50,80,110 D.20,80,110,50
第 2 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
9.观察下图的等高条形图,其中最有把握认为两个分类变量 x, y之间没有关系的是( )
A. B.
C. D.
10.为了规定工时定额,需要确定加工某种零件所需的时间,为此进行了 5 次试验,得
到 5 组数据: x1, y1 , x2 , y2 , x3, y3 , x4 , y4 , x5 , y5 ,由最小二乘法求得回归直线方程为
y 0.67x 54.9.若已知 x1 x2 x3 x4 x5 150,则 y1 y2 y3 y4 y5 ( )
A.75 B.155.4
C. 375 D. 466.2
11.下列极坐标方程中,对应的曲线为右图的
是( )
A. 6 5cos B. 6 5sin
C. 6 5cos D. 6 5sin
第 3 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
12.一次数学考试共有 8道判断题,每道题 5分,满分 40分.规定正确的画√,错误的画╳.
甲、乙、丙、丁四名同学的解答及得分情况如表所示,则 m的值为( )
题号
1 2 3 4 5 6 7 8 得分
学生
甲 ╳ √ ╳ √ ╳ ╳ √ ╳ 30
乙 ╳ ╳ √ √ √ ╳ ╳ √ 25
丙 √ ╳ ╳ ╳ √ √ √ ╳ 25
丁 ╳ √ ╳ √ √ ╳ √ √ m
A.35 B.30
C.25 D.20
第Ⅱ卷
二、填空题共 4小题,每小题 5分,共 20 分。
13.拉萨市政府调查市民收入增减与旅游需求的关系时,采用独立性检验法抽查了 5000人,
计算发现K 2 6.109,根据这一数据,市政府断言市民收入增减与旅游需求有关的可信
度是______%.
参考数据:
P K 2 k0 0.15 0.10 0.05 0.025 0.010 0.001
k0 2.072 2.706 3.841 5.024 6.635 10.828
14.1 i i2 i3 i2024 .
A 4, π B 2, π 15.在极坐标系中,点 , ,则线段 AB的长为 .
6 2
16.已知复数 z 1 2i,若 in z( n N*)在复平面内对应的点位于第四象限,写出一个满
足条件的 n是__________.
第 4 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
三、解答题共 6小题,共 70 分。解答应写出文字说明,演算步骤或证明过程。
3 i
17.(共 10分)已知复数 z ( i是虚数单位).
2 i
(1)求复数 z的共轭复数;
2 2( )若 z az b z a,b R ,求 a,b的值.
18.(共 12分)某大学艺术专业 400名学生参加某次测评,根据男、女学生人数比例使用
分层随机抽样的方法从中随机抽取了 100名学生,记录他们的分数,将数据分成 7组:
[20,30),[30,40),…,[80,90],并整理得到如图的频率分布直方图:
(1)估计总体 400名学生中分数小于 60的人数;
(2)已知样本中分数小于 40的学生有 5人,试估计总体中分数在区间[40,50)内的人数.
第 5 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
x 2cos
19.(共 12 分)在平面直角坐标系 xOy中,曲线C的参数方程为 (其中 为
y 2 2sin
参数).以坐标原点为极点, x轴非负半轴为极轴建立极坐标系,直线 l的极坐标方程为
2 cos π 4.
4
(1)求直线 l的直角坐标方程和曲线C的普通方程;
(2)设直线 l与曲线C交于 A,B两点,求线段 AB的长度.
20.(共 12 分)垃圾是人类日常生活和生产中产生的废弃物,由于排出量大,成分复杂多
样,且具有污染性,所以需要无害化、减量化处理.某省为调查产生的垃圾数量,采用
简单随机抽样的方法抽取 20 个县城进行了分析,得到样本数据 xi , yi i 1,2, , 20 ,
其中 xi 和 yi分别表示第 i个县城的人口(单位:万人)和该县年垃圾产生总量(单位:
20 20 20 20
2 2
吨),并计算得 xi 80 , yi 4000 , xi x 80 , yi y 8000 ,
i 1 i 1 i 1 i 1
20
xi x yi y 700.
i 1
(1)求这 20个县年垃圾产生总量的平均值;
(2)请用相关系数说明该组数据中 y与 x之间的关系可用线性回归模型进行拟合.(当
0.75 r 1时, y与 x的相关关系较强,否则相关关系较弱.)
n
xi x yi y
i 1
参考公式:相关系数 r n n .
x 2 2i x yi y
i 1 i 1
第 6 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
21.(共 12 分)随着互联网的发展,网络已成为人们日常学习、工作和生活不可或缺的部
分,互联网在带给人们生活便捷与高效工作的同时,网络犯罪也日益增多.为了防范网
络犯罪与网络诈骗,某学校举办“网络安全宣传倡议”活动.该学校从全体学生中随机抽
取了 100名男生和 100名女生对“网络安全宣传倡议”的了解情况进行问卷调查.下面是
问卷调查得分的频率分布表:
成绩(分) [40,50) [50,60) [60,70) [70,80) [80,90) [90,100]
频率 0.075 0.2 0.3 0.25 0.15 0.025
将得分不低于 70分的学生视作了解,已知有 50名男生问卷调查得分不低于 70分.
(1)根据已知条件完成下面 2 2列联表;
男 女 合计
了解
不了解
合计
(2)判断是否有95%的把握认为对“网络安全宣传倡议”的了解情况与性别有关?
n ad bc 22 参考公式:K ,其中 n a b c d .
a b c d a c b d
参考数据:
P K 2 k0 0.10 0.05 0.010 0.005
k0 2.706 3.841 6.635 7.879
第 7 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
22.(共 12分)如图所示形如花瓣的曲线G称为四叶玫瑰线,在极坐标系中,其极坐标方程
为 2sin 2 .
(1)若射线 l: 与G相交于异于极点O的点P,求 OP ;
6
π
(2)若 A, B为G上的两点,且 AOB ,求 AOB面积的最大值.
4
第 8 页 共 8 页
{#{QQABRQAEogioQBIAABBCQwmSCACQkgCACIgOhBAcIEAACQNABCA=}#}
同课章节目录
