实数复习[下学期]
图片预览






文档简介
课件17张PPT。第三章实数复习课平 方 根的定义:如果一个数的平方等于a,那么这个数叫做a的平方根(二次方根).x =a,2x叫做a的平方根性质1、正数有正、负两个平方根,它们互为相反数;
2、零的平方根是零;
3、负数没有平方根。平方根的表示方法: 一个正数a的正平方根用 表示,读作根号a; a的负平方根用 - 表示,读作负根号a,因此一个正数a的平方根就用 表示,读作“正负根号a”,其中a叫做被开方数。求一个数的平方根的运算叫做开平方。求一个数的立方根的运算,叫做开立方3.3 立方根 1.一个正数有一个正的立方根;
2. 一个负数有一个负的立方根;
3.零的立方根是零。 = a = a1、判断正误:
(1) 的立方根是
(2)负数不能开立方
(3)4的平方根是2
(4) -8 的立方根是-2
(5)负数有一个平方根
(6)0的立方根是0
(7) √16的平方根是2
2、下列计算正确的是( )
(1)√196=±14 (2)± √324=18
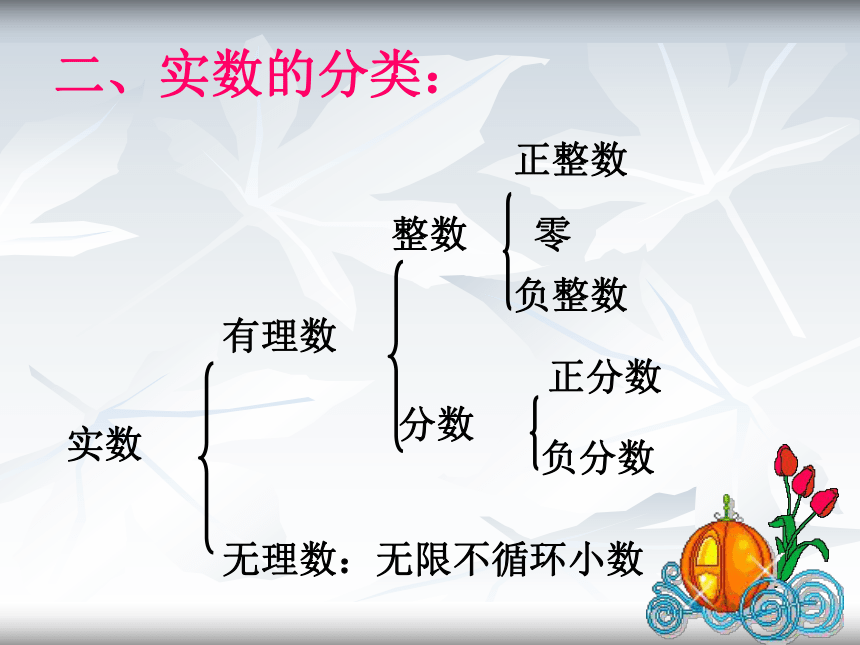
(3) √(-10)2=-10 (4)-√0.81=-0.9( )( )( )( )( )( )( )一、复习回顾1、无理数的定义:无限不循环小数叫做无理数2、有理数的定义:有限和无限循环小数叫做有理数或整数与分数统称为有理数二、实数的分类:有理数整数分数正整数零负整数正分数负分数无理数:无限不循环小数实数0.3737737773……1、把下列各数分别填入相应
的集合内:有理数集合无理数集合0.3737737773……0判断下列说法是否正确:(1)无限小数都是无理数(2)无理数都是无限小数(3)带根号的数都是无理数(4)实数都是无理数(5)无理数都是实数;(6)没有根号的数都是有理数( )( )( )( )( )( )比一比,看谁反应快3、实数的性质: 在实数范围内,相反数、倒数、
绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。例如:4、求下列各数的相反数、倒数和绝对值:22-77三、想一想 是一个实数,它的相反数为 ;
绝对值为 .如果 那么它的
倒数为 .四、议一议0-1121AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗?在数轴上作出 的对应点.0123-112 每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的. 同样,在数轴上,右边的点表示的数比左边的点表示的数大.数轴上一个点一个实数一个实数数轴上一个点小组合作交流 这节课你有何收获,
能与大家分享、交流你的感受吗? 谢谢合作再见
2、零的平方根是零;
3、负数没有平方根。平方根的表示方法: 一个正数a的正平方根用 表示,读作根号a; a的负平方根用 - 表示,读作负根号a,因此一个正数a的平方根就用 表示,读作“正负根号a”,其中a叫做被开方数。求一个数的平方根的运算叫做开平方。求一个数的立方根的运算,叫做开立方3.3 立方根 1.一个正数有一个正的立方根;
2. 一个负数有一个负的立方根;
3.零的立方根是零。 = a = a1、判断正误:
(1) 的立方根是
(2)负数不能开立方
(3)4的平方根是2
(4) -8 的立方根是-2
(5)负数有一个平方根
(6)0的立方根是0
(7) √16的平方根是2
2、下列计算正确的是( )
(1)√196=±14 (2)± √324=18
(3) √(-10)2=-10 (4)-√0.81=-0.9( )( )( )( )( )( )( )一、复习回顾1、无理数的定义:无限不循环小数叫做无理数2、有理数的定义:有限和无限循环小数叫做有理数或整数与分数统称为有理数二、实数的分类:有理数整数分数正整数零负整数正分数负分数无理数:无限不循环小数实数0.3737737773……1、把下列各数分别填入相应
的集合内:有理数集合无理数集合0.3737737773……0判断下列说法是否正确:(1)无限小数都是无理数(2)无理数都是无限小数(3)带根号的数都是无理数(4)实数都是无理数(5)无理数都是实数;(6)没有根号的数都是有理数( )( )( )( )( )( )比一比,看谁反应快3、实数的性质: 在实数范围内,相反数、倒数、
绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。例如:4、求下列各数的相反数、倒数和绝对值:22-77三、想一想 是一个实数,它的相反数为 ;
绝对值为 .如果 那么它的
倒数为 .四、议一议0-1121AB 如图:OA=OB,数轴上A点对应的数是什么? 如果将所有有理数都标到数轴上,那么数轴被填满了吗?在数轴上作出 的对应点.0123-112 每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的. 同样,在数轴上,右边的点表示的数比左边的点表示的数大.数轴上一个点一个实数一个实数数轴上一个点小组合作交流 这节课你有何收获,
能与大家分享、交流你的感受吗? 谢谢合作再见
