23.2.1 中心对称1 同步练习(含答案)人教版数学九年级上册
文档属性
| 名称 | 23.2.1 中心对称1 同步练习(含答案)人教版数学九年级上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 665.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 14:33:40 | ||
图片预览


文档简介
23.2.1 中心对称1
一、基础题
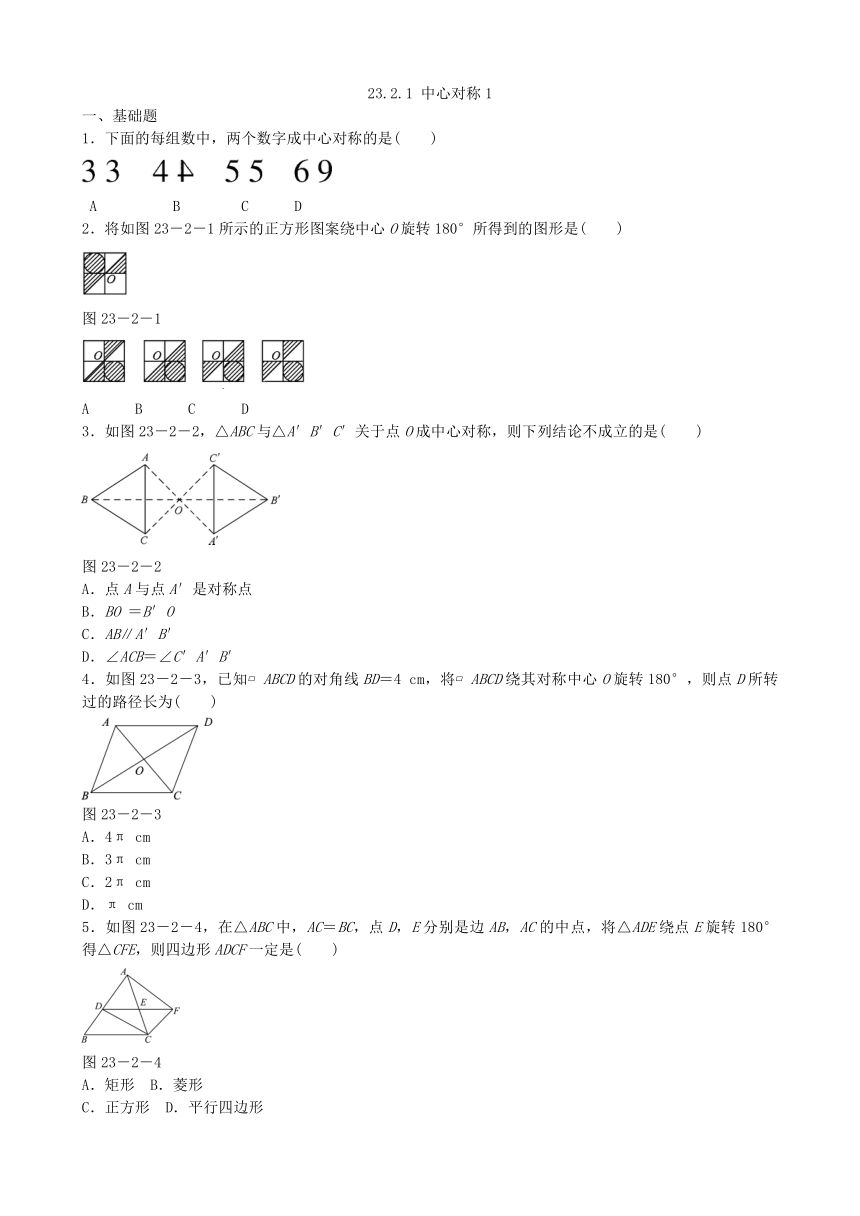
1.下面的每组数中,两个数字成中心对称的是( )
A B C D
2.将如图23-2-1所示的正方形图案绕中心O旋转180°所得到的图形是( )
图23-2-1
A B C D
3.如图23-2-2,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
图23-2-2
A.点A与点A′是对称点
B.BO =B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
4.如图23-2-3,已知 ABCD的对角线BD=4 cm,将 ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )
图23-2-3
A.4π cm
B.3π cm
C.2π cm
D.π cm
5.如图23-2-4,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
图23-2-4
A.矩形 B.菱形
C.正方形 D.平行四边形
6.如图23-2-5,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是_ __.
图23-2-5
7.如图23-2-6,菱形ABCD与菱形EFGH的形状、大小完全相同.
图23-2-6
(1)请从下列序号中选择正确选项的序号填空:
①点E,F,G,H; ②点G,F,E,H;
③点E,H,G,F; ④点G,H,E,F.
如果图(1)经过一次平移后得到图(2),那么点A,B,C,D的对应点分别是____;
如果图(1)经过一次轴对称后得到图(2),那么点A,B,C,D的对应点分别是____;
如果图(1)经过一次旋转后得到图(2),那么点A,B,C,D的对应点分别是____.
(2)①图(1),图(2)关于点O成中心对称,请画出对称中心(保留画图痕迹,不写画法);
②写出两个图形成中心对称的一条性质:__ __.(可以结合所画图形叙述)
8.如图23-2-7,已知△ABC和点O.
(1)在图中画出△A′B′C′,使△A′B′C′与△ABC关于O点中心对称;
(2)点A,B,C,A′,B′,C′能组成哪几个平行四边形?请用符号表示出来.
图23-2-7
二、能力提升
9.如图23-2-8所示,已知AD是△ABC的中线.
(1)画出以点D为对称中心,与△ABC成中心对称的三角形;
(2)若AB=6 cm,AC=4 cm,则AD的范围是______________.
图23-2-8
10.如图23-2-9所示,已知MN⊥PQ,垂足为点O,点A1,A关于MN对称,而点A2,A关于PQ
对称,请说明点A1,A2是以点O为对称中心的对称点.
11.如图23-2-10(1)所示,在梯形ABCD中,AD∥BC,AB=AD+BC.①取DC的中点E;②连接AE并延长到F,使EF=AE,如图23-2-10(2)所示.
(1)B,C,F三点共线吗?为什么?
(2)△ABF是什么三角形?为什么?
图23-2-10
12.如图23-2-11,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;……照此规律重复下去,则点P2013的坐标为__ __.
图23-2-11
答案:
1. D 2.C 3.D 4.C 5.A 6.(3,-1)
7.(1)①②④
(2)答案不唯一,例如:对应线段相等,OC=OE等
8.解:(1)如图所示:
(2) ABA′B′, BCB′C′, CA′C′A
9.解:(1)如图所示,延长AD至E,使DE=DA,连接CE,BE,则△ECB为求作的三角形.
(2)易证△ADB≌△EDC,则AB=CE.
又CE-AC∴2 cm<2AD<10 cm,
∴1 cm图23-2-9
10.解:如图所示.连接A1O,AO,A2O.
∵点A,A1关于MN对称,点O在对称轴MN上,
∴AO=A1O,∠1=∠2,
同理得AO=A2O,∠3=∠4,
∴A1O=AO=A2O.
又∵∠1+∠2+∠3+∠4=2(∠2+∠3)=2×90°=180°,
∴点A1,O,A2在同一条直线上,
∴A1,A2是以点O为对称中心的对称点.
11.解:(1)B,C,F三点共线.理由如下:
由作图知△ECF与△AED关于点E成中心对称,
所以∠D=∠ECF.
又因为∠D+∠BCD=180°,
所以∠BCE+∠ECF=180°,
所以B,C,F三点共线.
(2)由(1)知AD=CF,
因为AB=AD+BC,
所以AB=BC+CF,
即AB=BF,
所以△ABF是等腰三角形.
12.(0,- 2)
一、基础题
1.下面的每组数中,两个数字成中心对称的是( )
A B C D
2.将如图23-2-1所示的正方形图案绕中心O旋转180°所得到的图形是( )
图23-2-1
A B C D
3.如图23-2-2,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
图23-2-2
A.点A与点A′是对称点
B.BO =B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
4.如图23-2-3,已知 ABCD的对角线BD=4 cm,将 ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )
图23-2-3
A.4π cm
B.3π cm
C.2π cm
D.π cm
5.如图23-2-4,在△ABC中,AC=BC,点D,E分别是边AB,AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
图23-2-4
A.矩形 B.菱形
C.正方形 D.平行四边形
6.如图23-2-5,在平面直角坐标系中,若△ABC与△A1B1C1关于E点成中心对称,则对称中心E点的坐标是_ __.
图23-2-5
7.如图23-2-6,菱形ABCD与菱形EFGH的形状、大小完全相同.
图23-2-6
(1)请从下列序号中选择正确选项的序号填空:
①点E,F,G,H; ②点G,F,E,H;
③点E,H,G,F; ④点G,H,E,F.
如果图(1)经过一次平移后得到图(2),那么点A,B,C,D的对应点分别是____;
如果图(1)经过一次轴对称后得到图(2),那么点A,B,C,D的对应点分别是____;
如果图(1)经过一次旋转后得到图(2),那么点A,B,C,D的对应点分别是____.
(2)①图(1),图(2)关于点O成中心对称,请画出对称中心(保留画图痕迹,不写画法);
②写出两个图形成中心对称的一条性质:__ __.(可以结合所画图形叙述)
8.如图23-2-7,已知△ABC和点O.
(1)在图中画出△A′B′C′,使△A′B′C′与△ABC关于O点中心对称;
(2)点A,B,C,A′,B′,C′能组成哪几个平行四边形?请用符号表示出来.
图23-2-7
二、能力提升
9.如图23-2-8所示,已知AD是△ABC的中线.
(1)画出以点D为对称中心,与△ABC成中心对称的三角形;
(2)若AB=6 cm,AC=4 cm,则AD的范围是______________.
图23-2-8
10.如图23-2-9所示,已知MN⊥PQ,垂足为点O,点A1,A关于MN对称,而点A2,A关于PQ
对称,请说明点A1,A2是以点O为对称中心的对称点.
11.如图23-2-10(1)所示,在梯形ABCD中,AD∥BC,AB=AD+BC.①取DC的中点E;②连接AE并延长到F,使EF=AE,如图23-2-10(2)所示.
(1)B,C,F三点共线吗?为什么?
(2)△ABF是什么三角形?为什么?
图23-2-10
12.如图23-2-11,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;……照此规律重复下去,则点P2013的坐标为__ __.
图23-2-11
答案:
1. D 2.C 3.D 4.C 5.A 6.(3,-1)
7.(1)①②④
(2)答案不唯一,例如:对应线段相等,OC=OE等
8.解:(1)如图所示:
(2) ABA′B′, BCB′C′, CA′C′A
9.解:(1)如图所示,延长AD至E,使DE=DA,连接CE,BE,则△ECB为求作的三角形.
(2)易证△ADB≌△EDC,则AB=CE.
又CE-AC
∴1 cm
10.解:如图所示.连接A1O,AO,A2O.
∵点A,A1关于MN对称,点O在对称轴MN上,
∴AO=A1O,∠1=∠2,
同理得AO=A2O,∠3=∠4,
∴A1O=AO=A2O.
又∵∠1+∠2+∠3+∠4=2(∠2+∠3)=2×90°=180°,
∴点A1,O,A2在同一条直线上,
∴A1,A2是以点O为对称中心的对称点.
11.解:(1)B,C,F三点共线.理由如下:
由作图知△ECF与△AED关于点E成中心对称,
所以∠D=∠ECF.
又因为∠D+∠BCD=180°,
所以∠BCE+∠ECF=180°,
所以B,C,F三点共线.
(2)由(1)知AD=CF,
因为AB=AD+BC,
所以AB=BC+CF,
即AB=BF,
所以△ABF是等腰三角形.
12.(0,- 2)
同课章节目录
