华师大版数学九年级上册 第23章3 课题 相似图形教案
文档属性
| 名称 | 华师大版数学九年级上册 第23章3 课题 相似图形教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 17:27:08 | ||
图片预览

文档简介
课题 相似图形
1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形的性质和概念;
2.会利用相似图形的性质和概念进行计算和证明.
相似图形的性质和概念.
相似图形的性质的运用.
一、情景导入 感受新知
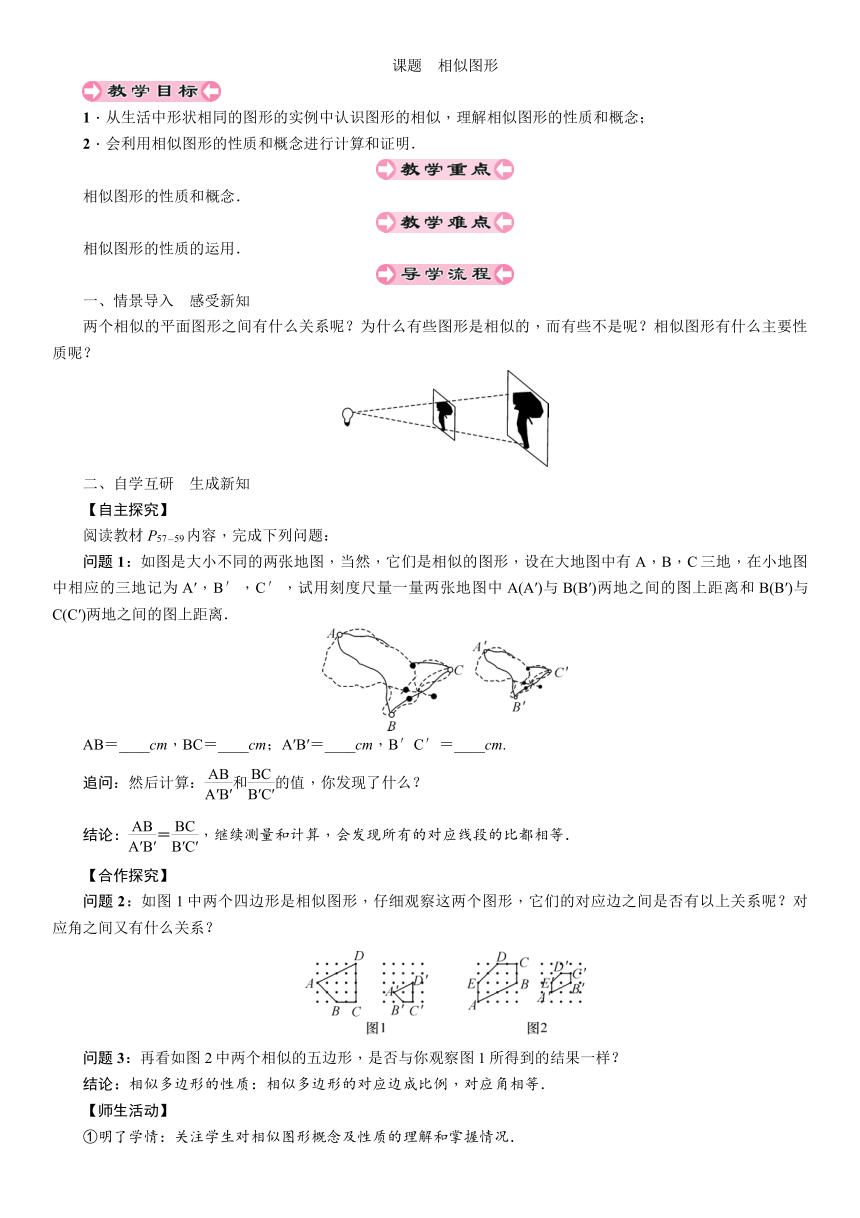
两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些不是呢?相似图形有什么主要性质呢?
二、自学互研 生成新知
【自主探究】
阅读教材P57-59内容,完成下列问题:
问题1:如图是大小不同的两张地图,当然,它们是相似的图形,设在大地图中有A,B,C三地,在小地图中相应的三地记为A′,B′,C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离和B(B′)与C(C′)两地之间的图上距离.
AB=____cm,BC=____cm;A′B′=____cm,B′C′=____cm.
追问:然后计算:和的值,你发现了什么?
结论:=,继续测量和计算,会发现所有的对应线段的比都相等.
【合作探究】
问题2:如图1中两个四边形是相似图形,仔细观察这两个图形,它们的对应边之间是否有以上关系呢?对应角之间又有什么关系?
问题3:再看如图2中两个相似的五边形,是否与你观察图1所得到的结果一样?
结论:相似多边形的性质:相似多边形的对应边成比例,对应角相等.
【师生活动】
①明了学情:关注学生对相似图形概念及性质的理解和掌握情况.
②差异指导:对探究中学生存在的疑惑及时引导,点拨.
③生生互助:学生小组内交流讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
【例1】在下图所示的相似四边形中,求边x的长度和角α的大小.
解:∵两个四边形相似,∴=,∴x=27,根据对应角相等,可得α=360°-(77°+83°+116°)=84°.
【变式迁移】
如图,四边形ABCD和EFGH相似,求角α、β的大小和EH的长度x.
解:∵四边形ABCD与EFGH相似.∴α=∠C=83°,∠A=∠E=118°,在四边形ABCD中,β=360°-(78°+83°+118°)=81°.∵四边形ABCD与EFGH相似,∴=即=,∴x=28.
【例2】如图,△ABC与△DEF相似,∠B,∠E为钝角,求未知边x,y的长度.
解:(1)∵△ABC∽△DEF,∴==即==,∴x=12,y=7.
(2)∵△ABC∽△FED,∴==即==,∴x=,y=.
四、课堂小结 回顾新知
教师指导学生总结本节课所学的基本内容和存在的疑惑点,建议学生积极发言,教师了解学生的掌握情况及存在的问题.
①本节课所学习的基本知识有哪些?
②学习本节课后,还有哪些疑惑?
五、检测反馈 落实新知
1.相似多边形指的是(D)
A.各角都相等的多边形
B.各边都相等的多边形
C.各边都成比例的多边形
D.边数相等,对应角相等,对应边成比例的多边形
2.请把下列各组图形是否相似的结论写在下面的括号里.
3.如图所示的每组四边形都相似,则
(1)如图①,x=__2.5__,y=__1.5__,α=__90°__;
(2)如图②,x=__22.5__.
六、课后作业 巩固新知
见学生用书.
1.从生活中形状相同的图形的实例中认识图形的相似,理解相似图形的性质和概念;
2.会利用相似图形的性质和概念进行计算和证明.
相似图形的性质和概念.
相似图形的性质的运用.
一、情景导入 感受新知
两个相似的平面图形之间有什么关系呢?为什么有些图形是相似的,而有些不是呢?相似图形有什么主要性质呢?
二、自学互研 生成新知
【自主探究】
阅读教材P57-59内容,完成下列问题:
问题1:如图是大小不同的两张地图,当然,它们是相似的图形,设在大地图中有A,B,C三地,在小地图中相应的三地记为A′,B′,C′,试用刻度尺量一量两张地图中A(A′)与B(B′)两地之间的图上距离和B(B′)与C(C′)两地之间的图上距离.
AB=____cm,BC=____cm;A′B′=____cm,B′C′=____cm.
追问:然后计算:和的值,你发现了什么?
结论:=,继续测量和计算,会发现所有的对应线段的比都相等.
【合作探究】
问题2:如图1中两个四边形是相似图形,仔细观察这两个图形,它们的对应边之间是否有以上关系呢?对应角之间又有什么关系?
问题3:再看如图2中两个相似的五边形,是否与你观察图1所得到的结果一样?
结论:相似多边形的性质:相似多边形的对应边成比例,对应角相等.
【师生活动】
①明了学情:关注学生对相似图形概念及性质的理解和掌握情况.
②差异指导:对探究中学生存在的疑惑及时引导,点拨.
③生生互助:学生小组内交流讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
【例1】在下图所示的相似四边形中,求边x的长度和角α的大小.
解:∵两个四边形相似,∴=,∴x=27,根据对应角相等,可得α=360°-(77°+83°+116°)=84°.
【变式迁移】
如图,四边形ABCD和EFGH相似,求角α、β的大小和EH的长度x.
解:∵四边形ABCD与EFGH相似.∴α=∠C=83°,∠A=∠E=118°,在四边形ABCD中,β=360°-(78°+83°+118°)=81°.∵四边形ABCD与EFGH相似,∴=即=,∴x=28.
【例2】如图,△ABC与△DEF相似,∠B,∠E为钝角,求未知边x,y的长度.
解:(1)∵△ABC∽△DEF,∴==即==,∴x=12,y=7.
(2)∵△ABC∽△FED,∴==即==,∴x=,y=.
四、课堂小结 回顾新知
教师指导学生总结本节课所学的基本内容和存在的疑惑点,建议学生积极发言,教师了解学生的掌握情况及存在的问题.
①本节课所学习的基本知识有哪些?
②学习本节课后,还有哪些疑惑?
五、检测反馈 落实新知
1.相似多边形指的是(D)
A.各角都相等的多边形
B.各边都相等的多边形
C.各边都成比例的多边形
D.边数相等,对应角相等,对应边成比例的多边形
2.请把下列各组图形是否相似的结论写在下面的括号里.
3.如图所示的每组四边形都相似,则
(1)如图①,x=__2.5__,y=__1.5__,α=__90°__;
(2)如图②,x=__22.5__.
六、课后作业 巩固新知
见学生用书.
